基于GBDT的线上交易欺诈侦测研究

赵金涛， 邱雪涛， 何东杰(中国银联 电子支付国家工程实验室， 上海 201201)

基于GBDT的线上交易欺诈侦测研究

赵金涛， 邱雪涛， 何东杰
(中国银联 电子支付国家工程实验室， 上海 201201)

随着银行卡行业的迅猛发展，在带来海量银行卡交易的同时，欺诈交易也与之俱增。将GBDT算法应用于银行卡欺诈侦测领域，通过WOE和IV方法对变量进行分组处理及筛选，以Bagging的方式对模型进行了组合，通过加权投票方式判断欺诈交易。实证研究表明，该模型的达到预期评价指标，效果显著。

GBDT; Bagging; 欺诈侦测

0 引言

近年来，随着我国社会经济的快速发展和居民消费水平的不断提高，银行卡产业发展势头迅猛。根据央行公布数据，2015年我国银行卡在用发卡量达到54.42亿张，交易852.29亿笔，金额669.82万亿元；银行卡欺诈率为1.99BP(每万元中发生的欺诈金额占比)，欺诈损失率为0.13BP。以此计算，我国2015年银行卡欺诈金额总计1 392.6亿元，银行卡欺诈损失约87亿元[1]。而随着移动支付及互联网业务的快速发展，银行卡欺诈风险开始向线上交易转移。相对于传统欺诈案件，网络支付渠道的欺诈表现出犯罪隐蔽、涉案区域分散、犯罪链条长等特点，风控难度更大。

由于银行卡欺诈给银行、收单机构及银行卡组织带来了巨大的风险及损失，各机构也积极采取措施进行银行卡欺诈侦测工作。目前，银行卡欺诈侦测主要有两种方式，一种是利用业务人员的专家经验或者通过统计方法形成规则或评分方法，然后通过规则引擎对交易进行判别，这种方式形成的规则结果解释性较好，但是严重依赖于专家经验，无法发现新的欺诈模式；另一种则是采用数据挖掘的方式，通过决策树、神经网络[2]等算法对历史交易数据进行学习，形成欺诈侦测模型，然后通过模型对交易进行判别。这种方式不依赖专家经验，可发现新的欺诈模式，并且欺诈侦测效果准确，受到越来越多研究人员的关注。但是这种方式在实际应用中存在着以下问题：1) 样本数据具有严重的不平衡性，欺诈交易占比只有万分之几，而这会导致模型趋向于将交易判别为正常交易，影响欺诈侦测效果；2) 传统的数据挖掘方式受限于单机计算能力，对于大规模样本无能为力，降采样或者抽样会影响模型效果。

基于上述问题，本文以中国银联的移动支付及互联网交易为分析基础，试图通过数据挖掘的方式，使用GBDT(又称Gradient Boosted Decision Tree或者Grdient Boosted Regression Tree)算法，建立一个更为准确的银行卡欺诈侦测模型。

1 GBDT算法

决策树是传统的分类方法之一，具有模型结构简单、易于理解、训练过程快速等优点。然而，单棵决策树在模型的训练过程中容易出现过拟合现象。为了弥补单棵决策树的缺陷，通常采用集成学习的方式，训练一组基分类器，然后通过对每个基分类器给予不同的权重，共同参与分类预测。GBDT是一个基于迭代累加的决策树集成算法，它通过构造一组弱的分类器(树)，并把多颗决策树的结果累加起来作为最终的预测输出。GBDT由回归树、Gradient Boosting等两个主要概念组成，下面逐一进行介绍。

(1) 回归树

GBDT通常采用CART(Classification And Regression Tree)作为基分类器，CART是由Breiman、Friedman、Olshen和Stone于1984年提出的一种决策树算法[3]，既可以做分类，也可以做回归，如果目标变量是离散变量，则是分类树，如果目标是连续变量，则是回归树。

CART的本质是对数据进行分类，每个节点会分成2个子节点，在形成二叉树的过程中，不断迭代寻找最佳分割点，最后形成一颗二叉树。

对于连续特征X={X1,…,Xn}，选择一个特征Xi(Xi∈X)，首先将特征Xi取值升序排序；两个特征取值之间的平均值点作为可能的分隔点，将数据集分成两部分，计算不纯度衡量指标，根据不纯度衡量指标选择最佳分割点。遍历所有特征，找到最佳特征及该特征的最佳分割点。树的生长，总原则是让子节点比树节点更纯，对于回归树通常采用最小平方残差、最小绝对残差等不纯度指标衡量。

(2) Gradient Boosting

Boosting 是 Kearns&Valiant 提出的一种分类学习方法。首先会为每个训练样本赋予一样的权重值，在每一次迭代进行训练模型时，会提高分错样本的权重，降低分对样本的权重。然后迭代了N次之后，得到N个弱的分类器，最后集成起来成为一个强分类器。

Gradient Boosting与Boosting的不同点在于，每一次训练的目的是为了减少上一次的残差，为了不断的降低残差，需要在减少残差的梯度方向训练一个新的模型。Gradient Boosting训练每一个新的模型都是为了模型在之前的模型的残差在梯度方向上降低。

2 基于GBDT算法的线上交易欺诈侦测模型

(1) 数据准备

样本标记

本文以2015年中国银联线上交易数据为研究对象，按月份抽取数据样本，银行卡发生过欺诈交易，其当天所有交易均标记为欺诈交易。正常交易与欺诈交易分别标记为0和1。正常交易数量为10亿+条记录，欺诈交易与正常交易比例约为1：10 000。

训练数据

本文以2015年1-8月份的抽样数据作为训练数据。其中正常交易样本排除所有发生过欺诈交易的卡片的交易数据。

测试数据

本文以2015年9-12月份的全量数据作为测试数据。

(2) 特征工程

变量生成

按当笔交易、同卡号上笔交易、当笔交易与上笔交易衍生变量、短时统计量、长时统计量、卡片历史交易特征等维度，选取了134个征变量。

数据清洗

根据业务需求对无意义的变量值赋空：若数据中已知某些变量的数值是无意义的，则需将该类数值置为空值，避免影响后续的计算。例如：后台商户的IP地址和IP所属省、市。

数据分组(WOE值及IV值计算)

WOE(Weight of Evidence)值可以衡量自变量取值对目标变量的一种影响，可以通过WOE值的计算对自变量进行离散化编码[4]。

对数值型变量的分组，根据变量数值大小，将建模样本分割为10组或20组，每组样本个数尽量相近，计算每组的WOE值，为式(1)。

(1)

其中Gi、Bi分别代表第i个分组内正常交易及欺诈交易的数量；G、B分别代表总体正常交易及欺诈交易的数量。

对字符型变量的分组，根据变量的不同值，将建模样本分组，计算每组的WOE值。

IV(Information Value)值代表某一个变量的信息量，是该变量的各个特征的WOE值的加权总和，IV值代表了该变量区分目标变的能力，为式(2)。

(2)

同时可以根据IV值的取值来进行变量的筛选。

IV值变量预测能力IV<0．02无0．02≤IV<0．1弱0．1≤IV<0．3中等0．3≤IV<0．5强IV≥0．5强有力

(3) 建模过程

本文将训练及测试数据存放于Hive表中，通过Spark SQL读取数据，然后通过Spark MLlib 的Pipeline将数据处理、模型训练及测试等步骤封装起来。其中算法采用Spark MLlib中的GBDT算法。

为了提升模型效果，我们采用Bagging的方式训练模型及并进行测试，即对正常样本有放回的采样并进行训练得到多个模型，然后通过多个模型以投票的方式决定交易是正常交易还是欺诈交易。

(4) 实证结果分析

这里将银行卡欺诈侦测问题归结为一个分类问题，采用欺诈交易的覆盖率、准确率以及F1值作为模型的评价指标，为式(3)～(5)。

(3)

(5)

测试场景1

采用2015年1-8月的数据作为训练数据，分别以单个模型以及Bagging的方式对2015年9月份的数据进行测试，其中Bagging方式采用20个模型参与投票预测。测试结果如表1所示。

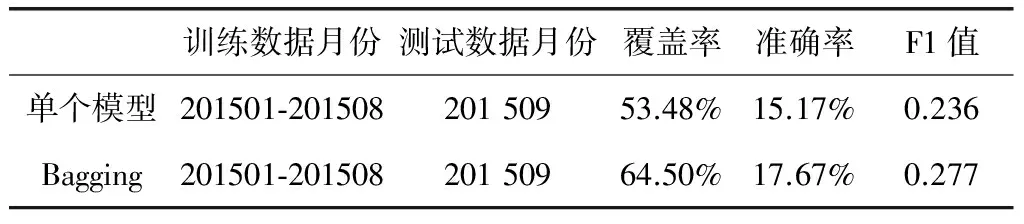
表1 单个模型与Bagging方式测试结果对比

上表数据表明，在同等条件下， 通过Bagging方式形成的组合模型在覆盖率、准确率、F1值等指标上均超越单个模型，也进一步说明Bagging对提升模型效果的有效性。

测试场景2

采用2015年1-8月的数据作为训练数据，以Bagging的方式分别对2015年9-12月份的数据进行测试，其中Bagging方式采用20个模型参与投票预测。测试结果如表2所示。

表2 同一模型对不同数据的测试结果对比

上表数据表明，模型的分类效果存在着不稳定性，分类效果随时间呈下降趋势。

测试场景3

分别以2015年1-8月、2015年1-9月、2015年1-10月的数据作为训练数据，以Bagging的方式分别对2015年11月份的数据进行测试，其中Bagging方式采用20个模型进行参与投票预测。测试结果，如表3所示。

表3 不同训练数据对同一测试数据的测试结果对比

上表数据表明，训练样本数据越多，在时间维度上越接近测试数据，模型的分类效果越好，分类结果也越准确。

3 总结

实证研究表明，本文基于GBDT建立的线上交易欺诈侦测模型可以很好的检测欺诈交易，通过以Bagging方式将多个弱分类器组合成一个强分类器，对于模型有着很好的提升效果；研究同时表明随着时间的推移， 模型稳定性及分类能力呈下降趋势，为了避免这种情况，需要定期将最新的欺诈样本参与模型训练，以保证模型的稳定性及准确性。

[1] 人民银行有关负责人答记者问：http://www.pbc.gov.cn/goutongjiaoliu/113456/113469/3139454/index.html.

[2] 童凤茹.基于组合分类器的信用卡欺诈识别研究[J].计算机与信息技术,2006(7):10-12.

[3] Breiman L J H, Friedman R A, Olshen C J Stone. Classification and Regression Trees[M]. New York: Chapman and Hall, 1984.

[4] 阚士行.商业银行信用评级筛选财务指标方法效果对比与校验[D].济南：山东大学,2010.

ResearchonOnlineTransactionFraudDetectionBasedonGBDT

Zhao Jintao, Qiu Xuetao, He Dongjie
(National Engineering Laboratory for Electronic Commerce and Electronic Payment, China UnionPay, Shanghai 201201)

The rapid development of bank card industry brought huge amounts of transactions, and fraud transactions also increased. This paper applied GBDT to the field of bank card fraud detection. It grouped data and filtered variables by the methods of WOE and IV, and then combined models by the strategy of Bagging and finally judged whether a transaction was a fraud transaction by a weighted voting algorithm. The empirical study shows that the model could achieve the expected evaluation index, and the effect was significant.

GBDT； Bagging； Fraud detection

TP181

A

2017.04.10)

上海市青年科技英才杨帆计划资助(17YF1425800)

赵金涛(1985-)，男，硕士，研究员，研究方向：大数据、风险防控。

邱雪涛(1981-)，男，硕士，经理，研究方向：大数据、风险防控。

何东杰(1984-)，男，硕士，经理，研究方向：大数据、云计算。

1007-757X(2017)10-0017-02