基于波动门限效应GARCH模型的波动率预测

王 沁，乔高秀

(西南交通大学 数学学院，四川 成都 610031)

基于波动门限效应GARCH模型的波动率预测

王 沁，乔高秀

(西南交通大学 数学学院，四川 成都 610031)

基于大的波动的稳定中心不同于小的波动的稳定中心的问题，提出一类具有波动门限效应的GARCH模型。研究了波动门限效应GARCH模型的参数估计，并通过AIC最小原则选择了门限阈值。根据MAE、RMSE和MAPE这3个损失函数，与传统GARCH模型的预测能力进行了比较分析。实证结果表明，波动门限效应GARCH模型在波动性预测方面比传统GARCH模型的效果更好。

波动门限效应；GARCH模型；AIC值;门限阈值；波动预测；损失函数

波动率是金融市场、金融资产最重要的特征之一。在投资组合、资产定价、风险管理及货币政策制定，都离不开波动率这一关键变量。随着国际金融市场的日趋规范、壮大，各金融机构之间的竞争发生了根本性变化，金融市场的不确定性和系统性风险不断增加。因此，波动性估计与预测成了金融领域研究的一个重要任务和关键问题。

在波动率模型中，应用最广泛的是广义自回归条件异方差模型(GARCH)。一方面， GARCH模型的波动率是异方差函数自相关过程，适用于波动性、持续性和聚集性的分析与预测；另一方面，GARCH模型的波动率是滞后残差平方和滞后条件方差的线性函数，不能反映正负价格变化对波动率的杠杆影响和波动非线性变化的特征。因此，越来越多的学者对GARCH模型的改良和扩展进行了研究, 旨在提高波动率预测的精度。如国外WANG等[1]应用广义指数分布改良了GARCH模型，该模型刻画了收益率分布的厚尾性，提高了波动率的预测精度。BHLMANN等[2]针对非参数GARCH模型提出了相应的算法。HOU等[3]应用非参数GARCH模型对原油收益率的波动率进行了预测，结果表明非参数GARCH 模型的预测能力明显优于参数GARCH模型。 ELLIOTT等[4-5]对马尔科夫转移机制下的GARCH 模型进行了实际应用和统计推断，从理论和应用两个层面表明马尔科夫转移机制下的GARCH 模型能够捕捉波动率在不同状态下的非对称、非线性的转换机制。POPOV等[6]最先提出模糊GARCH模型并研究离散时间序列的波动性。HELIN等[7-8]利用模糊GARCH模型对波动率进行了估计和预测，发现模糊GARCH模型的预测效果比GARCH模型好。在国内，许冰等[9-10]研究了非参数GARCH模型，指出非参数GARCH 模型对于波动性问题提供了一个有力的研究工具。蒋详林等[11-13]研究了MRS-GARCH 模型，表明马尔科夫转移机制下GARCH 模型的预测功能总体优于GARCH模型。鲁万波等[14]利用遗传算法对模糊GJR-GARCH模型的参数进行了估计，并成功地预测了收益率的波动率的时变性和非对称性。柳雪飞[15]利用遗传算法搜索门限GARCH模型的结构参数，并对收益率的波动进行了预测，发现门限GARCH模型的适应性更强，效果更好。

总结上述研究发现，针对门限GARCH模型的研究较少，为此笔者在前人研究的基础上，基于大的波动的稳定中心不同于小的波动的稳定中心的问题，提出一类具有波动门限的GARCH模型，通过AIC值最小原则选择了门限阈值，并根据MAE、RMSE和MAPE这3个损失函数，与传统GARCH模型的预测能力进行比较分析。

1 波动门限效应GARCH模型

1.1 波动门限效应GARCH模型的结构

传统GARCH模型为：

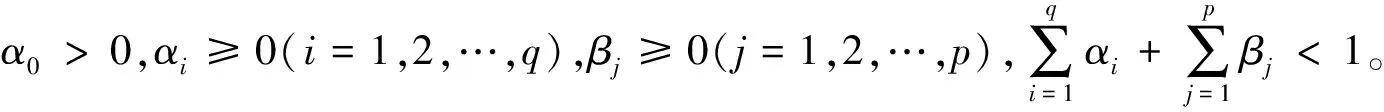
GARCH模型中条件方差为过去所有残差的正向加权平均，从而大的变化倾向于有更大的变化，小的变化倾向于有更小的变化，较好地描述了波动的持续性和集聚效应， 其波动的稳定中心为：

由于大的波动紧跟大的波动，小的波动紧跟小的波动， 所以大的波动的稳定中心应与小的波动的稳定中心不一致，波动的集聚效应也不一致，存在信息的非对称性，故在方差方程中引入波动的门限效应，方差方程的结构为：

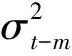
(4)

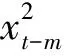
1.2 波动门限效应GARCH模型的参数估计

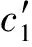
假设随机序列{et}服从标准正态分布，那么基于样本容量为n的对数似然函数为：

(7)

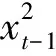
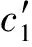
(8)

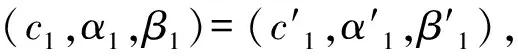
2 波动门限效应GARCH模型的实证研究

2.1 样本及数据来源

笔者选择ST黑化、ST中昌、亚太实业、申通地铁4只股票 2011年10月10日至2015年10月14日的每日对数收益率作为研究对象，数据来源于通信达软件。4只股票收益率序列图如图1所示。

由图1可以看出，无论是非ST公司还是ST公司，股票收益率序列都存在着非线性、异方差效应及非对称性，而且都是大的波动紧跟大的波动，小的波动紧跟小的波动。所以，大的波动的稳定中心应该与小的波动的稳定中心不一致，存在信息的非对称性，应建立波动门限效应GARCH(1,1)模型，来刻画金融数据的这种具有不同稳定中心的波动效应。

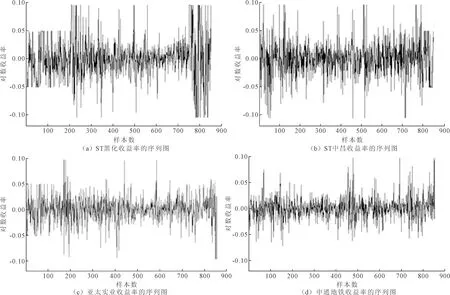
图1 4只股票收益率的序列图

2.2 参数的估计

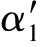
为了比较波动门限效应GARCH模型与传统GARCH模型的优良性，对ST黑化、ST中昌、亚太实业、申通地铁4只股票建立GARCH-N(1,1)模型，参数估计结果如表2所示。从表2可以看出，ST黑化、ST中昌、亚太实业和申通地铁的GARCH效应和ARCH效应都非常显著， GARCH效应都大于ARCH效应。这说明如果不构建门限GARCH模型，有可能对ARCH效应造成高估的结果。

随后，笔者利用似然比检验来验证是否存在显著的门限效应，门限存在性检验结果如表3所示。表3结果表明：①对于每家公司来说，运用波动门限效应GARCH模型求出的AIC值都比建立GARCH模型求出的AIC值小，所以建立波动门限效应GARCH模型更加适合。②计算得到的似然比统计量的值大于给定的显著性水平下对应的临界值,都显著地拒绝原假设，说明模型确实存在明显的门限效应。

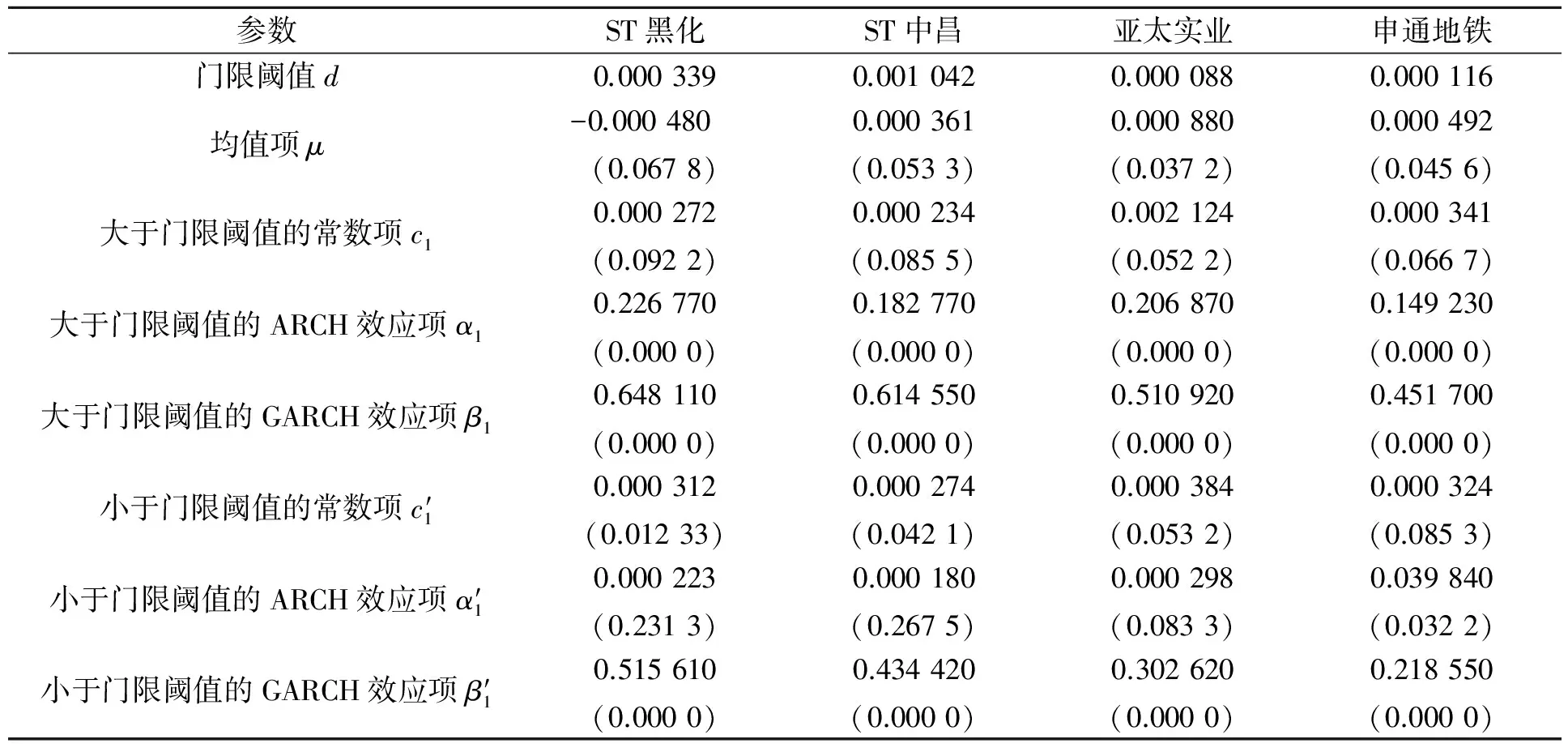
表1 波动门限效应GARCH模型的参数估计

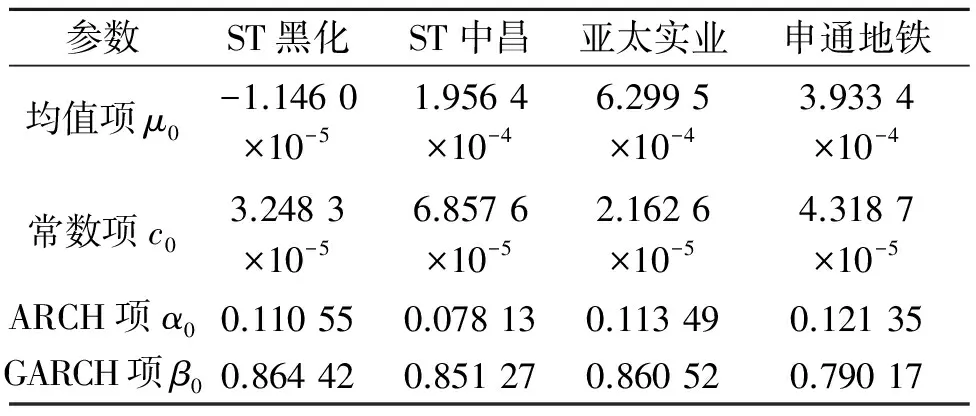
表2 GARCH-N(1,1)模型的参数估计

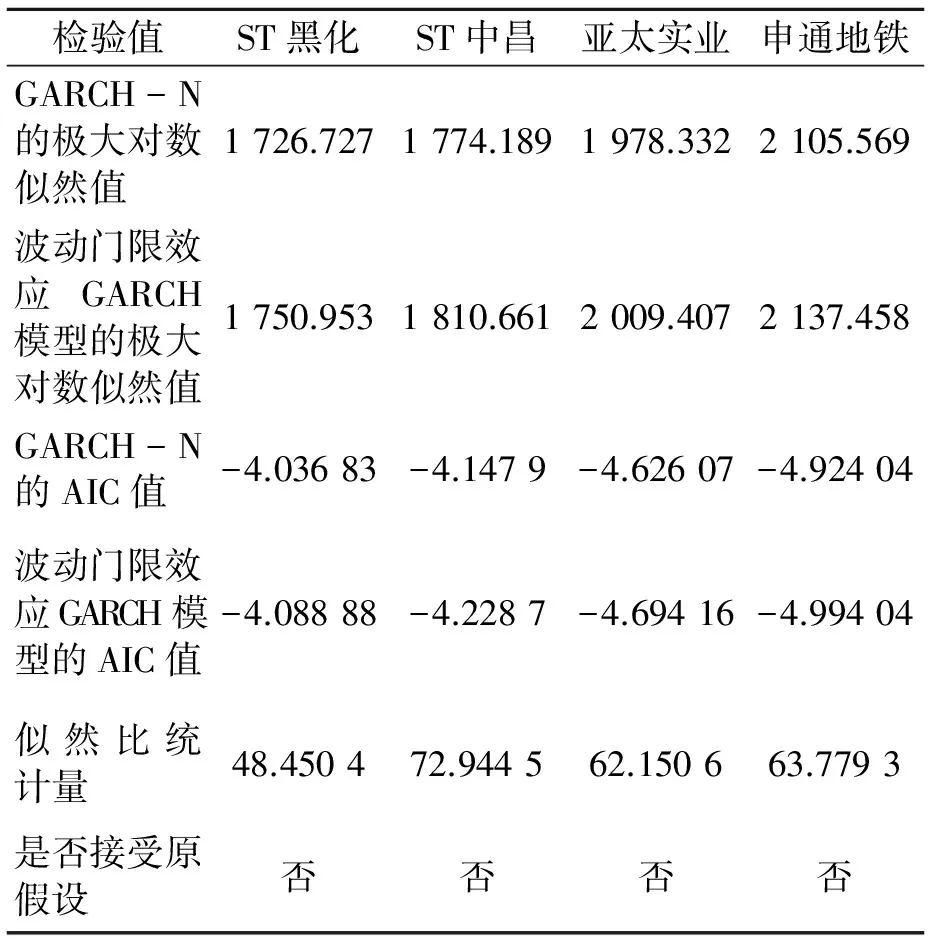
表3 门限存在性检验结果

2.3 波动率的预测

针对GARCH-N(1,1)模型，由于：

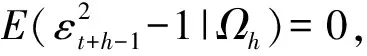
(9)

同理，针对波动门限GARCH-N(1,1)模型向前h(h>1)步的预测估计式为：

(10)

令T=R+P，其中R=845代表滚动窗口，P=11代表滚动时间，T代表样本容量，采用滚动窗口原则对波动率进行预测。第一步：取t=1，2，…,R；第二步：取t=2，3,…,R+1；第P步：取t=P，P+1,…,P+R-1，这样一来对每一期的预测可以得到11个预测值，并利用MAE(mean absolute error),RMSE(root mean squared error)和MAPE(mean absolute percentage error)3个损失函数来检验预测效果，这3个损失函数的定义如下：

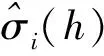
ST黑化的预测结果如表4所示，可以看出对于ST黑化，GARCH模型的MAE、RMSE和MAPE值都比波动门限GARCH模型要大一些，这说明利用门限GARCH模型对波动率的预测较为有效、准确。

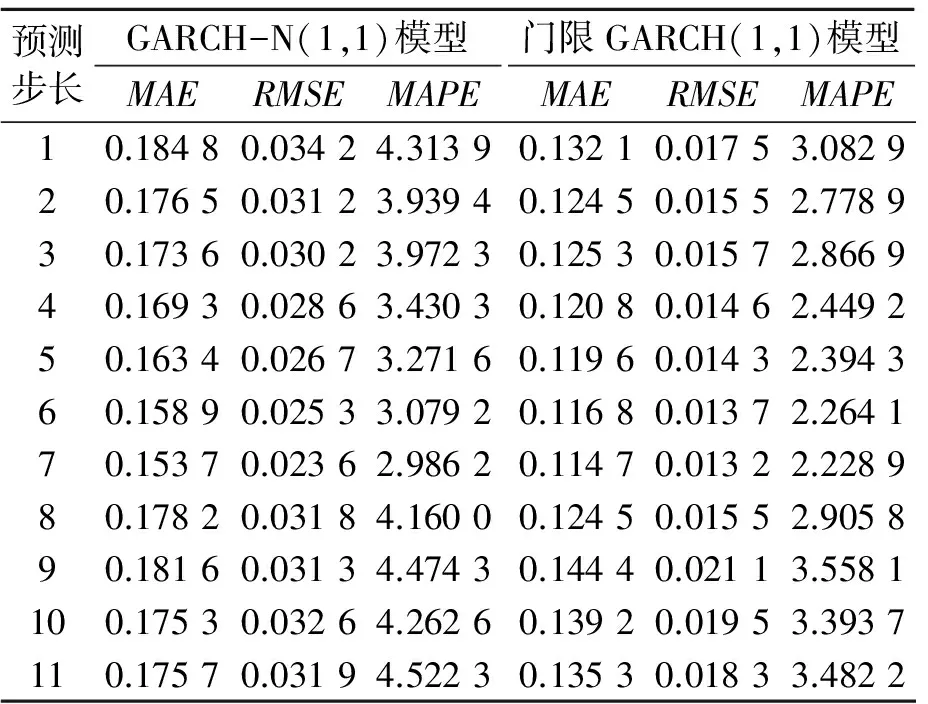
表4 ST黑化的模型预测比较

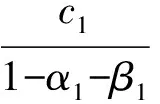
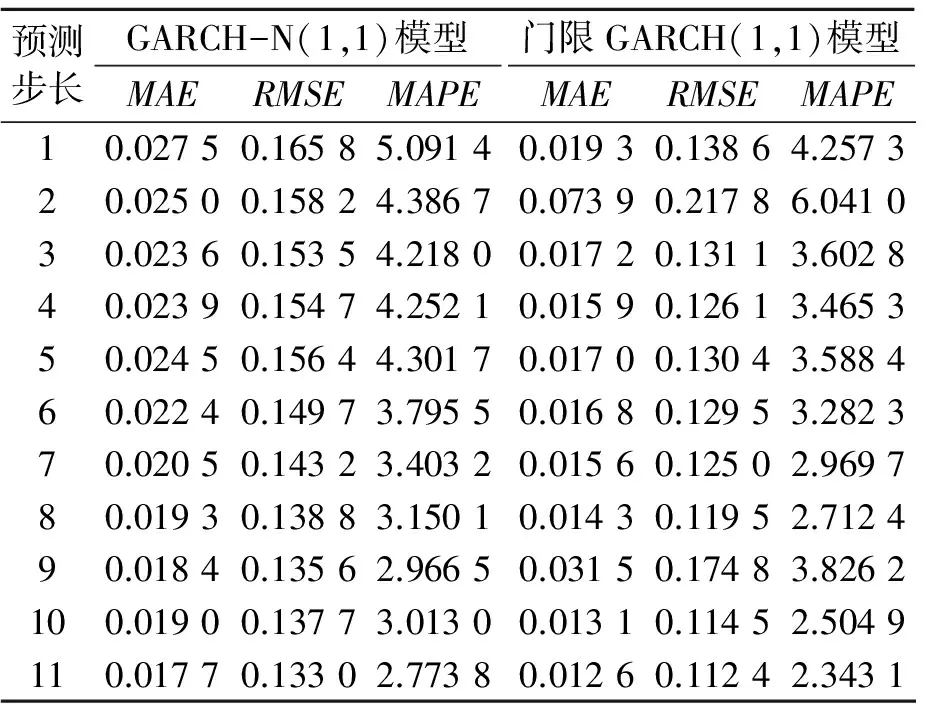
表5 ST中昌的模型预测比较

亚太实业、申通地铁的波动率的预测比较结果分别如表6和表7所示，可以看出对于亚太实业、申通地铁，GARCH模型的MAE、RMSE和MAPE值都比波动门限GARCH模型要大一些，这说明波动门限GARCH模型对股市波动性的预测精度有明显提高。

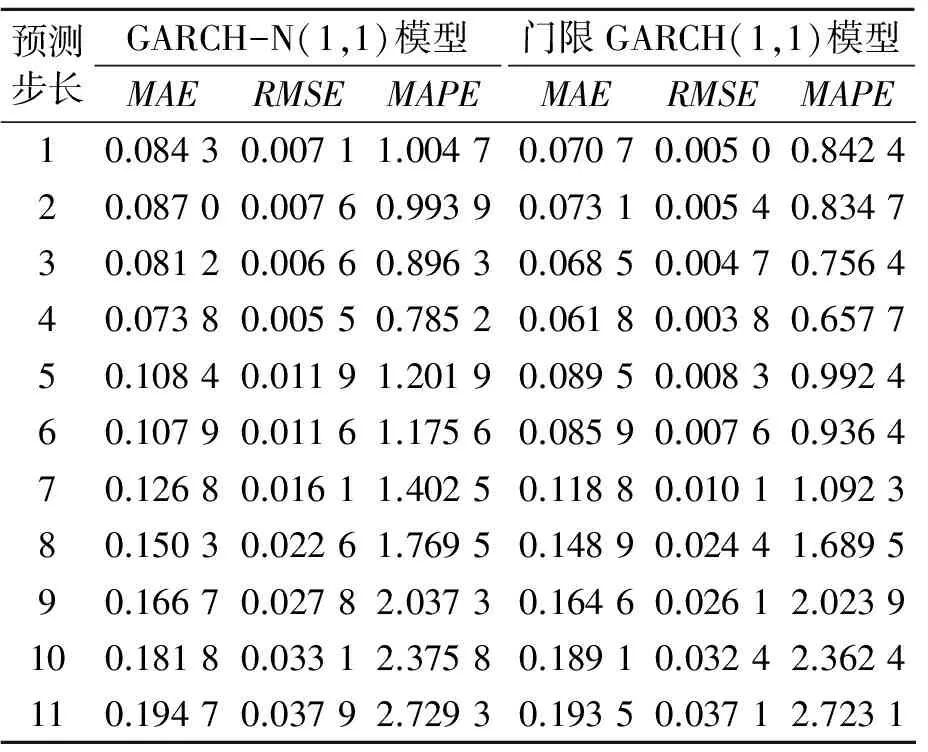
表6 亚太实业的模型预测比较

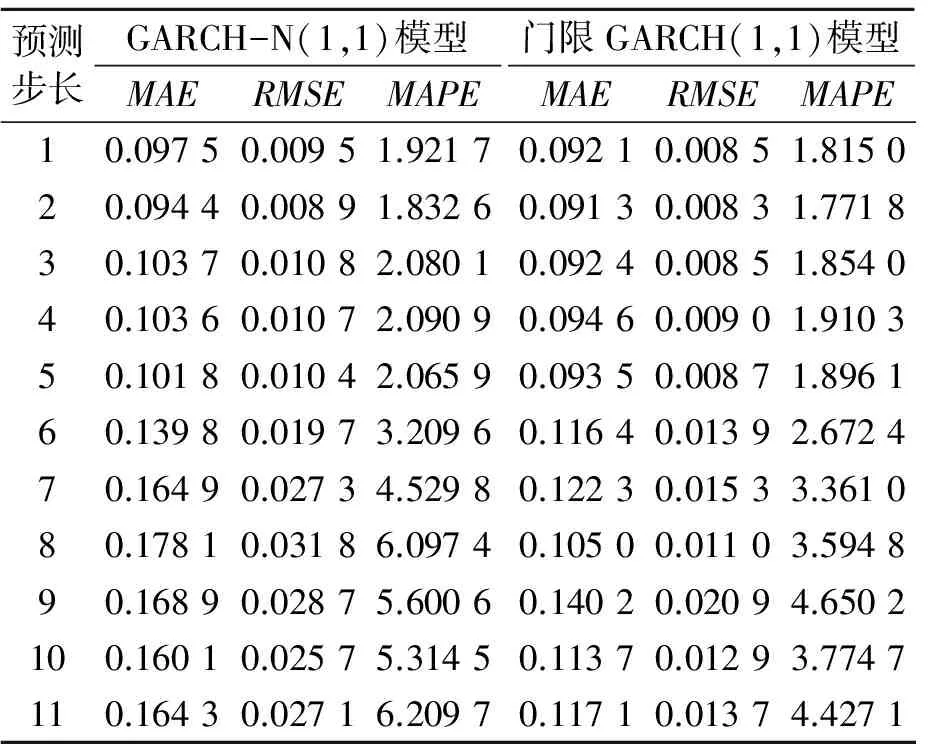
表7 申通地铁的模型预测比较

3 结论

笔者基于大的波动的稳定中心应与小的波动的稳定中心不一致，存在信息的非对称性，将波动门限效应引入到GARCH 模型中，从而刻画金融数据的这种非对称性GARCH模型的结构。实证研究发现：依赖于收益率平方的变化，波动门限GARCH模型相对于GARCH模型包含了更多信息，更能刻画波动率的时变性、集聚性、非对称性，在短期和长期波动率的预测能力上,比GARCH模型略胜一筹。

对于门限GARCH模型，选择什么样的变量作为门限是一个难题，例如，选择成交量作为门限变量，或者选择极差变量作为门限变量等。笔者只是基于稳定中心的不一致，选择了收益率的平方作为门限变量，与其他门限变量的GARCH模型没有进行比较。另外，笔者的波动门限GARCH模型与MRS-GARCH模型在形式具有相似性，波动率的转换是存在马尔科夫转换机制，还是由于超过某个阈值自然产生的转换，这一问题有待未来进一步研究。

[1] WANG K L, FAWSON C, BARRETT C B,et al. A flexible parametric GARCH model with an application to exchange rates[J]. Journal of Applied Econometrics, 2001,16(4):521-536.

[3] HOU A ,SUARDI S. A nonparametric GARCH model of crude oil price return volatility [J]. Energy Economic , 2012,34(2):618-625.

[4] ELLIOTT R J, SIU T K, CHAN L.Option price for GARCH model with Markov switching[J].International Journal of Theoretical and Applied Finance,2006,9(6)：825-841.

[5] BAUWENS L,PREMINGER A,ROMBOUTS J V K. Theory and inference for a Markov switching GARCH model [J]. Journal of Economic, 2010,13(2):218-244.

[6] POPOV A A, BYKHANOV K V. Modeling volatility of time series using fuzzy GARCH model[C]∥International Conference on Fuzzy Sets and Soft Computing in Economics and Finance.[S.l.]:IEEE, 2005:687-692.

[7] HELIN T,KOIVISTO H.The GARCH-fuzzy density method for density forecasting[J]. Applied Soft Computation, 2011,11(6):4212-4225.

[8] ALMEIDA R J,BASTURK N,KAYMAK U. Conditional density estimation using fuzzy GARCH models[J].Advances in Intelligent Systems and Computing, 2013,190(13):173-181.

[9] 许冰,任军峰.基于非参数GARCH一种波动率估计方法[J].统计与决策，2006(19)：6-7.

[10] 赵树然，任培民，赵昕.基于非参数GARCH模型的汇率波动性预测[J].统计与决策，2012(6)：148-151.

[11] 蒋详林,王春峰,吴晓霖.基于状态转移模型的中国股市波动性研究[J].系统工程学报,2004,19(3):270-277.

[12] 孙金丽, 张世英.具有结构转换的模型及其在中国股市中的应用[J].系统工程,2003,21(6):86-91.

[13] 赵华，蔡建文.基于MRS-GARCH模型的中国股市波动率估计与预测[J].数理统计与管理，2011,30(5):912-921.

[14] 鲁万波, 焦鹏.基于模糊GJR-GARCH模型的波动率估计[J].数理统计与管理，2014,33(3)：912-921.

[15] 柳雪飞.遗传门限GARCH模型及其应用研究[D].武汉：武汉科技大学，2011.

TheVolatilityForecastBasedontheFluctuationThresholdEffectGARCHModel

WANGQin,QIAOGaoXiu

Based on the stability center of a large fluctuation is different from that of a small one, a special GARCH model with fluctuation threshold effect is proposed. How to estimate these parameters in the fluctuation threshold effect GARCH model is researched. The threshold value is selected by the minimum principle of the AIC value. The forecasting ability is compared between the traditional GARCH model and the fluctuation threshold GARCH model through three loss function( MAE, RMSE and MAPE). The results show that the fluctuation threshold effect GARCH model is better than the traditional GARCH model in terms of volatility forecasting.

fluctuation threshold effect; GARCH model; AIC value;threshold value; volatility forecast; losses function

F064.1

10.3963/j.issn.2095-3852.2017.05.013

2095-3852(2017)05-0575-06

A

2017-05-22.

王沁(1973-),女,四川夹江人,西南交通大学数学学院副教授,博士，主要研究方向为金融数量分析、时间序列分析、非参数统计与风险管理.

国家自然科学基金项目(71371157)；教育部人文社会科学研究青年基金项目(17YJC790119).

WANGQinAssoc. Prof.; School of Mathematics,Southwest Jiaotong University, Chengdu 610031,China.