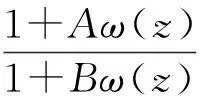一类与In算子有关的解析函数的Fekete-Szegö不等式

2017-11-02李宗涛

华南师范大学学报（自然科学版） 2017年5期

关键词：积分算子子类滁州

郭栋，李宗涛

(1. 滁州职业技术学院基础部，滁州 239000； 2. 广州民航职业技术学院基础部，广州 510403)

一类与In算子有关的解析函数的Fekete-Szegö不等式

郭栋1*，李宗涛2

(1. 滁州职业技术学院基础部，滁州 239000； 2. 广州民航职业技术学院基础部，广州 510403)

单叶函数；In算子；Q(a,n;A,B)函数； Fekete-Szegö不等式

When the parameters ofa,AandBare assigned with some special values, Fekete-Szegö inequalities of some special function class are obtained.

Keywords： univalent function;Inoperator;Q(a,n;A,B) function; Fekete-Szegö inequality

令H表示形如

f(z)=z+a2z2+a3z3+…

(1)

且在U={z:|z|<1}内解析的函数f(z)的全体所成的函数类.H中单叶函数全体记作S. 如果f(z)H，且满足Re{zf′(z)/f(z)}>0，则称函数f(z)为单位圆U内的星形函数，记作S*.

对于f(z)H,RUSCHEWEYH[2]定义算子D:H→H,D=*f(z) (f(z)H;>-1),并称之为Ruscheweyh导数. 类似地，NOOR[3]定义了如下算子：

In:H→H,Inf(z)=[z/(1-z)](-1)*f(z)=

(2)

显见I0f(z)=zf′(z),I1f(z)=f(z).

FEKETE和SZEGÖ[4]于1933年证明了：设f(z)S，f(z)由式(1)给出，0≤μ<1，则且对每个μ等号都成立.

学者们研究了H中一些子类的Fekete-Szegö问题[5-9],但对于In算子定义的函数类上的Fekete-Szegö问题研究很少. 本文研究了Q(a,n;A,B)函数类上的Fekete-Szegö问题，推广了一些已有的结果.

下面给出算子In定义上的函数类Q(a,n;A,B).

定义1对于-1≤B

(Inf(z))′+az(Inf(z))″(zU),

(3)

记函数f(z)Q(a,n;A,B).

当参数a、B、A取特殊值时，可得一些特殊的解析函数类. 例如:

Q(0,n;1-2β,-1)=Re(Inf(z))′>β(zU)；

Q(0,1;1,-1)=Ref′(z)>0 (zU)；

Q(1,0;1,-1)=Re[f′(z)+3zf″(z)+z2f‴(z)]>0

(zU);

Q(0,0;1,-1)=Q(1,1;1,-1)=Re[f′(z)+zf″(z)]>0

(zU).

近年来，学者们研究了与NOOR算子相关的各种解析函数类和亚纯函数类[10-14]，如定义了函数类Q(a,n;A,B)，研究了此函数类的包含关系和函数f(z)属于此函数类的2个充要条件[10].

为了导出本文的主要结果，需要如下引理.

引理1[15]设ω(z)=d1z+d2z2+…(zU)解析,且|ω(z)|≤|z|,则|d1|≤1,|d2|≤1-|d1|2.

引理2[16]设p(z)=1+p1z+p2z2+…在U={z:|z|<1}内解析且满足Rep(z)>0，则

下面给出本文的主要结果.

定理1假设f(z)H由式(1)给出，f(z)Q(a,n;A,B)，u,则

证明因为f(z)Q(a,n;A,B)，所以存在ω(z)=d1z+d2z2+…，使得

(4)

将Inf(z)的幂级数展开式代入式(4)，并比较恒等式两边的z和z2两项的系数，可得

由引理1可得：

H(x)=C+CDx2,

其中

E=8B(1+a)2(n+2)+9u(1+2a)(A-B)(n+1).

所以

相应地,极值函数为：

(Inf(z))′=

推论1假设Re(Inf(z))′>β(0≤β<1),f(z)由式(1)给出，u,则

且对所有的u等号都成立.

在推论1中令n=1,β=0，则得：

推论2[17]假设Ref′(z)>0,f(z)由式(1)给出，u,则

且对所有的u等号都成立.

推论3假设Re[f′(z)+3zf″(z)+z2f‴(z)]>0，f(z)由式(1)给出，u,则

且对所有的u等号都成立.

推论4假设Re[f′(z)+zf″(z)]>0，f(z)由式(1)给出，u,则

且对所有的u等号都成立.

利用引理2，类似于定理1的证明可以得到以下定理：

且对所有的u等号都成立.

[1] CATAS A,OROS G I,OROS G. Differential subordinations associated with multiplier transformations[J]. Abstract and Applied Analysis,2008(3):1563-1569.

[2] RUSCHEWEYH S. New criteria for univalentfunctions[J]. Proceedings of the American Mathematical Society,1975,49:109-115.

[3] NOOR K I,NOOR M A. On integral operators[J]. Journal of Mathematical Analysis and Applications,1999,238:341-352.

[4] FEKETE M,SZEGÖ G. Eine Bermerkung uberungerade schlichte funktionen[J]. Journal of the London Mathematical Society,1933,8(1):85-89.

[5] 郭栋,李宗涛,杨家稳. 一类解析函数类的Fekete-Szegö不等式[J]. 华南师范大学学报(自然科学版),2012,44(4):28-30.

GUO D,LI Z T,YANG J W. The Fekete-Szegö inequlitity for some subclasses of analytic functions[J]. Journal of South China Normal University(Natural Science Edition),2012,44(4):28-30.

[6] 崔志峰,刘名生. 用卷积定义的解析函数子类的Fekete-Szegö不等式[J]. 数学杂志，2011,31(5):954-961.

CUI Z F,LIU M S. Fekete-Szegö inequalities for certain subclasses of analytic functions defined by convolution[J]. Journal of Mathematics,2011,31(5):954-961.

[7] GUO D,LI Z T,HUANG J C. On the Fekete-Szegö problem for a class of analytic functions[J]. Chinese Quarterly Journal of Mathematics,2015,30(3):442-449.

[8] 郭栋,李宗涛. 一类解析函数类的Fekete-Szegö不等式[J]. 华南师范大学学报(自然科学版),2017,49(3):114-116.

GUO D,LI Z T. The Fekete-Szegö inequlitity for a subclass of analytic functions[J]. Journal of South China Normal University(Natural Science Edition),2017,49(3):114-116.

[9] 鲍春梅,李书海. 一类β级扩展的Bazilevic函数及其Fekete-Szegö问题[J]. 华南师范大学学报(自然科学版),2010(3):7-10.

BAO C M,LI S H. A class ofβrank espanded Bazilevic function and Fekete-Szegö problem[J]. Journal of South China Normal University(Natural Science Edition),2010(3):7-10.

[10] 施冬芳,鲁大前,王敏. 由Noor积分算子定义的解析函数的性质[J]. 扬州大学学报(自然科学版)，2008,11(1):1-4.

SHI D F,LU D Q,WANG M. Properties of analytic functions defined by Noor integral operator[J]. Journal of Yangzhou University(Natural Science Edition),2008,11(1):1-4.

[11] 刘文娟,彭娟,杨清. 与Noor积分算子有关的多叶解析函数子类的性质[J]. 扬州大学学报(自然科学版),2012,15(3):8-11.

LIU W J,PENG J,YANG Q. Properties of certain subclasses of multivalent analytic functions involving Noor integral operator[J]. Journal of Yangzhou University(Natural Science Edition),2012,15(3):8-11.

[12] 魏丽,刘名生. 涉及Noor多重积分算子的解析函数的中间定理[J]. 华南师范大学学报(自然科学版)，2010(2):9-13.

WEI L,LIU M S. Sandwich theorem of analytic functions involving Noor-multiplier integral operator[J]. Journal of South China Normal University(Natural Science Edition),2010(2):9-13.

[13] 仓义玲. 由算子In+p-1定义的解析函数的新子类[J]. 徐州师范大学学报(自然科学版),2009,27(1):43-45.

CANG Y L. Subclasses of analytic functions defined by the operatorIn+p-1[J]. Journal of Xuzhou Normal Vniversity(Natural Science Edition),2009,27(1):43-45.

[14] LIU J L,NOOR K I. On subordinations for certain analytic functions associated with Noor integral operator[J]. Applied Mathematics & Computation,2007,187(2):1453-1460.

[15] 夏道行,张开明. 关于从属函数的几个不等式[J]. 数学学报,1958,8(3):408-412.

XIA D X,ZHANG K M. Some ineqalities in the theory of subordination[J]. Acta mathematica Sinica1,1958,8(3):408-412.

[16] 刘名生. 某类解析函数的Fekete-Szegö不等式[J]. 数学物理学报,2002,22A(1):8-14.

LIU M S. The Fekete-Szegö inequality for certain class of analytic functions[J]. Acta Mathematica Scientia,2002,22A(1):8-14.

[17] 杨定恭. 关于一类解析函数[J]. 常熟高专学报,2001,15(2):1-12.

YANG D G. On a class of analytic functions[J]. Journal of Changshu College,2001,15(2):1-12.

The Fekete-Szegö Inequality for Some Subclass of Analytic Functions Related to InOperator

GUO Dong1*, LI Zongtao2

(1. Foundations Department, Chuzhou Vocational and Technical College, Chuzhou 239000, China;2. Foundations Department, Guangzhou Civil Aviation College, Guangzhou 510403, China)