全局性N元-强混沌系统的一个判据
2017-11-02符和满
符和满
(肇庆学院数学与统计学院, 肇庆 526061)
符和满*
(肇庆学院数学与统计学院, 肇庆 526061)
设(X,f)是一个动力系统,其中X是一个含至少2个点的完备度量空间,f是X上的一个连续自映射. 对给定的Furstenberg族与整数N≥2,将-混沌推广到N元-混沌. 为此,对于X的2个非空子集A、B,借助集对(A,B)的-往复点来引入-攀援串的概念,进而定义N元-混沌以及讨论N元-混沌的一些性质. 最后以Furstenberg族理论为主要工具,给出一个动力系统是全局性N元-强混沌的一个判据,并通过例子来阐述它在动力系统中的应用.
Furstenberg族; 全局性N元-强混沌;N元-攀援集
Keywords: Furstenberg family; generical strong-N-chaos;-N-scrambled set
设(X,f)是一个动力系统(简称系统),即X是一个含至少2个点的完备度量空间,f:X→X是一个连续映射;d表示度量空间X的度量.
2007年,XIONG等[1]对任意给定的Furstenberg族定义了-混沌,使得Li-Yorke混沌成为-混沌,分布混沌成为(1)-混沌,其中是正整数集的所有无限子集构成的Furstenberg族,(1)是所有上密度为1的正整数集构成的Furstenberg族;并且给出了全局性-强混沌系统的一个判据. 有关分布混沌更多内容可参阅文献[2-5].
为了更全面理解混沌本质,学者们进一步研究多元混沌. 例如,研究了Li-Yorke意义下的攀援N-串[6],进一步引入了N元分布混沌并得到它的初步性质[7],其中N≥2. 本文将文献[1]的-混沌推广到N元-混沌,类似地给出动力系统是全局性N元-强混沌的一个判据,并通过相应的例子来阐述此判据的应用,从而掌握到一些全局性N元-强混沌系统.
1 主要结果
首先简单介绍 Furstenberg 族, 所使用的概念和记号主要源于文献[8].

1.1 N 元-攀援集
设(X,f)为动力系统,是一个Furstenberg族. 下面所用的术语源于文献[1].
设A⊂X. 点xX称为集合A的一个-贴附点,如果点x在集合A中的回复时间集属于,即Nf(x,A). 集合A的所有-贴附点构成的集合称为集合A的-贴附集,记作(A,f). 明显地,有(A,f)=∪F∩nFf-n(A).
称点xX是集合A⊂X的一个-趋附点,如果对于任意实数δ>0,点x是集合[A]δ的-贴附点,即x([A]δ,f).
对于给定的实数δ>0,称点xX是集合A⊂X的一个-δ-逃匿点,如果x是集合X-的一个-贴附点. 称点xX是集合A⊂X的一个-逃匿点,如果存在某一个实数δ>0使得x是A的-δ-逃匿点.
设A、B是X的非空子集. 称点xX是集对(A,B)的一个-往复点(或-δ-往复点),如果它既是A的-趋附点,又是B的-逃匿点(相应地,-δ-逃匿点).
集合A的全体-趋附点(或-逃匿点,-δ-逃匿点)构成的集合α(A,f)(相应地,ε(A,f),ε(A,δ,f))称为集合A的-趋附集(相应地,-逃匿集,-δ-逃匿集). 集对(A,B)的全体-往复点(-δ-往复点)构成的集合θ(A,B,f)(θ(A,B,δ,f))称为集对(A,B)的-往复集(相应地,-δ-往复集). 则有
α
ε(A,δ,f)=(X-,f),ε(A,f)=ε(A,δ,f),
θ(A,B,δ,f)=α(A,f)∩ε(B,δ,f),
θ(A,B,f)=α(A,f)∩ε(B,f).

借助集对(A,B)的-往复点,下面给出-攀援串以及N元-攀援集的定义.
称X的子集C为系统(X,f)的一个N元-攀援集,如果对任意N个两两互异的点x1,…,xNC,(x1,…,xN)是一个-攀援串. 设实数δ>0,称X的子集C为系统(X,f)的一个N元-δ-攀援集,如果对任意N个两两互异的点x1,…,xNC,(x1,…,xN)是一个-δ-攀援串.
下面2个引理分析了集对(A,B)的-δ-往复集的性质,这些性质将用于定理1的证明.
引理1设是与系统(X,f)兼容的Furstenberg族,A、B是X的非空子集,则A的-趋附集α(A,f) 是X中的Gδ集,并且对于任意实数δ>0,集对(A,B)的-δ-往复集也是X中的Gδ集.
证明由于Furstenberg族是与系统(X,f)兼容的,任意开集的-贴附集是Gδ集,所以集合A的-趋附集作为可数个Gδ集之交是Gδ集. 由于集合B的-δ-逃匿集是一个Gδ集,集对(A,B)的-δ-往复集作为2个Gδ集之交仍是Gδ集. 证毕.
称两集合A、B⊂X(或者点xX和集合B⊂X)是正分离的,如果d(A,B)>0(相应地,d(x,B)>0).
引理2设A,B,C⊂X都是非空的且B、C是正分离的,则存在实数δ>0使得集合C的-趋附集α(C,f)包含在B的-δ-逃匿集ε(B,δ,f)中. 因此集对(A,B)的-δ-往复集θ(A,B,δ,f)包含A的-趋附集α(A,f)和C的-趋附集α(C,f)之交.
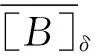
ε⊃⊃

因此θ(A,B,δ,f)=α(A,f)∩ε(B,δ,f)⊃α(A,f)∩α(C,f). 证毕.
定理1设是一个与系统(X,f)兼容的Furs-tenberg族,集合A,B⊂X是非空的. 存在与集合B正分离的非空集合C⊂X,使得A和C的-趋附集α(A,f)和α(C,f)都是稠密的当且仅当存在实数δ>0使得集对(A,B)的-δ-往复集θ(A,B,δ,f)是X中的稠密的Gδ集.
证明设存在非空集合C⊂X与B正分离,且α(A,f)和α(C,f)都是稠密的. 由引理1,α(A,f)和α(C,f)都是稠密的Gδ集. 由引理2,存在实数δ>0使得集对(A,B)的-δ-往复集θ(A,B,δ,f)包含稠密的Gδ集α(A,f)与α(C,f)之交,则θ(A,B,δ,f)是稠密的. 由引理1,θ(A,B,δ,f)是稠密的Gδ集.
反之,设存在实数δ>0使得集合θ(A,B,δ,f)是X中的稠密的Gδ集. 由于α(A,f)包含θ(A,B,δ,f),所以是稠密的. 令C=X-[B]δ,与B是正分离的. 由于
α(C,f)⊃(C,f)⊃(X-,f)=ε(B,δ,f)⊃
θ(A,B,δ,f),
所以C是非空的,并且α(C,f)是稠密的. 证毕.
1.2 全局性N元-强混沌系统的判据
设整数N≥2,下面定义全局性N元族-(强)混沌.
如果系统(X,f)中由-攀援串构成的集合是XN中的一个稠密的Gδ集,则称系统(X,f)是全局性N元-混沌的. 如果存在实数δ>0使得系统(X,f)中由-δ-攀援串构成的集合是XN中一个稠密的Gδ集,则称系统(X,f)是全局性N元-强混沌的.
由于系统(X,f)中由-攀援串(或者-δ-攀援串)构成的集合按定义是系统(XN,f(N))中集对的-往复集θ相应地,-δ-往复集θ所以将定理1应用于乘积系统(XN,f(N)),立即得到:
定理2设是一个与系统(X,f)的乘积系统(XN,f(N))兼容的Furstenberg族,其中整数N≥2. 系统(X,f)是全局性N元-强混沌的当且仅当Δ的-趋附集α(Δ,f(N))在XN中稠密,并且存在与正分离的非空子集A⊂XN,其-趋附集α(A,f(N))在XN中稠密.
引理3如果Ai(1≤i≤N)是X的N个子集,其中整数N≥2,i(1≤i≤N+1)是N+1个Furstenberg族,且1·2·…·N⊂N+1,则
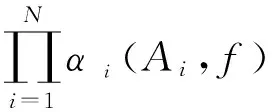
证明由积空间XN的性质,对任意的δ>0,存在δi>0 (i=1,2,…,N),使得


下面给出全局性N元-强混沌系统的一个判据.
定理3设是一个与系统(X,f)的乘积系统(XN,f(N))兼容的满的Furstenberg族,其中整数N≥2. 如果X中存在N个两两正分离的非空子集Ai(1≤i≤N),使得A1是一个单点集;Ai(i=1,2,…,N-1)的κ-趋附集ακ(Ai,f)稠密;AN的-趋附集α(AN,f)稠密,则系统(X,f)是全局性N元-强混沌的.


W⊂X称为f的不变子集,如果f(W)⊂W. 下面的推论是定理3的一种特殊情形,改进了文献[9]的结论:

2 应用
最近,XIONG等[10]引入如下一类新的 Furstenberg 族. 对任意(0,1],定义
其中Fc=+-F. 并且定义0=∩. 易见,对任意[0,1],均是Furstenberg族;且对任意的0≤1≤2≤1,有⊂. 实际上,1=(1).
设整数N≥2,首先将推论1应用于符号空间的转移系统(ΣN,σ),其中ΣN是N个符号的(单边)符号空间,σ是ΣN上的转移自映射.

例1说明了符号空间的转移系统是全局性N元-强混沌的,这一点在意料之中. 下面不在符号空间构造出一个看起来“不平凡”的动力系统(例2),它也是全局性N元-强混沌的,[0,1]. 为此,先回顾构造动力系统的一种方法[11-12].
设(X,f)、(Y,g)是2个动力系统,其中X、Y都是紧致度量空间. 设x0X是f的一个不动点. 把X×Y的子集{x0}×Y捏为一点,可得一个紧致度量空间,记作Xx0Y. 此时,f×g自然地诱导了Xx0Y上的一个连续自映射,设为h. 易知(Xx0Y,h)也是一个紧致的动力系统.
对xX,记Qx=π({x}×Y),其中π是(X×Y,f×g)到(Xx0Y,h)的因子映射,Qx0是一个单点集.
例2定义I=[0,1]上的一个逐段线性的连续自映射f:
显然,f有N个不动点,记作xi(i=1,2,…,N),其中x1=0. 令g是单位圆周S1上的一个无理旋转. 考虑动力系统(I0S1,h),则Qxi(i=1,2,…,N)是h的两两正分离的不变子集,且每一个在I0S1中稠密. 注意到Qx1=Q0是一个单点集,故对于与系统(I0S1,h)的N重乘积系统兼容的满的Furstenberg族,由推论1知系统(I0S1,h)是全局性N元-强混沌的.
注1例1与例2都是全局性N元0-强混沌系统,当然更是全局性N元强分布混沌系统. 由此看来,这类系统的混沌性质是非常强的.
[1] XIONG J C,LV J,TAN F. Furstenberg family and chaos[J]. Science in China:Series A,2007,50(9):1325-1333.
[2] 顾国生,熊金城. 关于分布混沌的一点注记[J]. 华南师范大学学报(自然科学版),2004(3):37-41.
GU G S,XIONG J C. A note on the distributional chaos[J]. Journal of South China Normal University(Natural Science Edition),2004(3):37-41.
[3] 简俊敏,吕杰. 树映射分布混沌的等价刻画[J]. 华南师范大学学报(自然科学版),2006(4):6-9.
JIAN J M,LV J. A sufficient and necessary condition of distributional chaos of tree maps[J]. Journal of South China Normal University(Natural Science Edition),2006(4):6-9.
[4] 李健,谭枫. 关于Li-Yorkeδ-混沌与按序列分布δ-混沌的等价性[J]. 华南师范大学学报(自然科学版),2010(3):34-38.
LI J,TAN F. The equivalence relationship between Li-Yorkeδ-chaos and distributionalδ-chaos in a sequence[J]. Journal of South China Normal University(Natural Science Edition),2010(3):34-38.
[5] 符和满,谭枫. 以全空间为-n-攀援集的系统[J]. 华南师范大学学报(自然科学版),2014(2):34-37.
FU H M,TAN F. Systems with the whole spaces being-n-scrambled[J]. Journal of South China Normal University(Natural Science Edition),2014(2):34-37.
[6] LI J. Chaos and entropy for interval maps[J]. Journal of Dynamics and Differential Equations,2011,23(2):333-352.
[7] TAN F,FU H M. On distributionaln-chaos[J]. Acta Mathematica Scientia,2014,34(5):1473-1480.
[8] AKIN E. Recurrence in topological dynamics:Furstenberg families and Ellis actions[M]. New York:Plenum Press,1997:23-51.
[9] 吕杰,熊金城,谭枫. 周期吸附系统的分布混沌[J]. 数学学报:中文版,2008,51(6):1109-1114.
LV J,XIONG J C,TAN F. Distributional chaos of periodically adsorbing system[J]. ACTA Mathematica Sinica:Chinese Series,2008,51(6):1109-1114.
[10] XIONG J C,FU H M,WANG H Y. A class of Furstenberg families and their applications to chaotic dynamics[J]. Science China Mathematics,2014,57:823-836.
[11] FU H M,XIONG J C,TAN F. On distributionally chaotic and null systems[J]. Journal of Mathematical Analysis and Applications,2011,375:166-173.
[12] HUANG W,YE X D. Homeoporphisms with the whole compacta being scrambled sets[J]. Ergodic Theory and Dynamical Systems,2001,21:77-91.
A Criterion for Generically Strong-N-chaotic Systems
FU Heman*
(School of Mathematics and Statistics, Zhaoqing University, Zhaoqing 526061, China)
Let(X,f) be a dynamical system, whereXis a complete metric space containing at least two points andfis a continuous self-map onX.-chaos is generalized to-N-chaos for a given Furstenberg familyand an integerN≥2. For this purpose,-scrambled tuples are defined by means of-reciprocating points with respect to a pair(A,B) of non-empty sets inX. Hence,-N-chaos is defined and some properties of-N-chaos are considered. Finally, a criterion for generically strong-N-chaotic systems is obtained by heavy use of the theory of Furstenberg families, and its applications in dynamical systems are given with two examples.
2016-01-25 《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n
广东省自然科学基金项目(S2013040013857)
*通讯作者:符和满,副教授,Email:dbfhm@163.com.
O19
A
1000-5463(2017)05-0092-04
【中文责编:庄晓琼 英文审校:肖菁】
