差分进化算法的研究进展
2017-11-02李斌
李 斌
(河南建筑职业技术学院,河南 郑州 450064)
差分进化算法的研究进展
李 斌
(河南建筑职业技术学院,河南 郑州 450064)
差分进化算法是一类当前较为强大的随机实参数优化算法,已成功解决很多实际问题。它具有全局优化性能好、结构简单易于实现、控制参数少和搜索能力强等优点,差分进化算法吸引了众多进化算法研究者的关注。文中详细概述了差分进化算法的基本概念、特点、改进和应用现状,就DE算法的进一步研究进行了探讨和展望。
差分进化;进化算法;遗传算法
1 引言
根据达尔文的生物进化理论,自然界的物种会随着客观环境的变化而发生变异,各个物种在竞争环境中生存,优胜劣汰,使得生物不断进化。为了求解复杂优化问题,一些研究人员尝试借鉴自然界物种进化的思想来开展优化算法研究,从而开启了一个重要研究方向——进化计算(Evolutionary Computation,简称EC)。进化计算具有稳健性、易实现性和全局搜索能力强等特点,同时不依赖待求问题的种类和性质,因此在众多领域倍受关注。
类似于其他的进化计算算法,差分进化(Differential Evolution,简称DE)算法也是一种基于种群的全局随机搜索算法[1],它最初是由Storn和Price为求解切比雪夫多项式拟合问题于1995年提出的。1996年5月在日本举行的第一届国际进化优化方法竞赛(International Contest on Evolutionary Optimization, ICEO)中,DE算法表现突出,获得了第三名的成绩。1997年的第二届国际进化优化方法竞赛中Price通过大量优化实验证明了DE是一种性能优异的进化算法。从此,DE算法得到更多研究者的关注。自2005年以来,在IEEE Conference on Evolution Computation(CEC)会议关于实参优化、多目标优化、动态不确定性优化等多次竞赛中,DE具有非常优异的表现。
DE算法是一种基于种群的智能优化方法,不依赖问题的特征信息,主要借助于种群个体之间的差分信息对个体形成扰动来探索整个种群空间,并利用贪婪竞争机制进行优化,寻求问题最优解。DE算法采用实数编码,首先在搜索空间内随机产生初始群体,使用变异操作、交叉操作生成新的个体,但与一般的进化算法不同的是,差分进化算法采用一对一的淘汰机制来更新进化群体,降低了进化操作的复杂性。不同的是差分进化算法把一定比例的多个个体的差分信息作为个体的扰动量,使得算法在跳跃距离和搜索方向上具有自适应性[2]。在进化的早期,因为种群中个体的差异性较大使得扰动量较大,从而使得算法能够在较大范围内搜索,具有较强的探索能力(exploration);而到了进化的后期,当算法趋向于收敛时,种群中个体的差异性较小,算法在个体附近搜索,这使得算法具有较强的局部开采能力(exploitation)[2]。
鉴于差分进化算法具有控制参数少、原理相对简单、易于理解和实现的优点,再加上其表现出来的高可靠性、强鲁棒性以及良好的优化性能,目前已经成为进化计算研究领域的热点。它广泛应用于很多领域,如控制系统与机器人、化学工程、模式识别与图像处理、人工神经网络、生物信息学和信号处理等取得了惊人的效果。
2 差分进化算法基本原理
DE的基本思想是:利用从种群中随机选择的两个个体向量的差分量作为第三个随机基准向量的扰动量,得到变异向量,然后变异向量与基准向量(或称为目标向量)进行交叉操作,生成试验向量。最后基准向量和试验向量竞争,较优者保存在下一代群体中。这样,差分进化算法逐代改善群体质量,引导种群聚焦到最优解位置。
图1给出了差分进化算法的主要步骤,包括种群初始化,以及选择多个个体进行变异操作产生变异个体,变异个体与目标个体进行交叉操作,目标个体与试验个体竞争选择操作等。从图1中我们可以看出,DE算法执行简单,易于实现。

图1 DE算法的主要步骤
2.1 初始化
个体每一维上的取值可按下式产生:

2.2 变异
在DE算法中,种群内个体的差分向量经过缩放之后,与种群内另外的相异个体相加得到变异向量。根据变异向量生成方法不同,形成了多种变异策略[3]。目前被广泛采用的五种变异策略如下[1]:
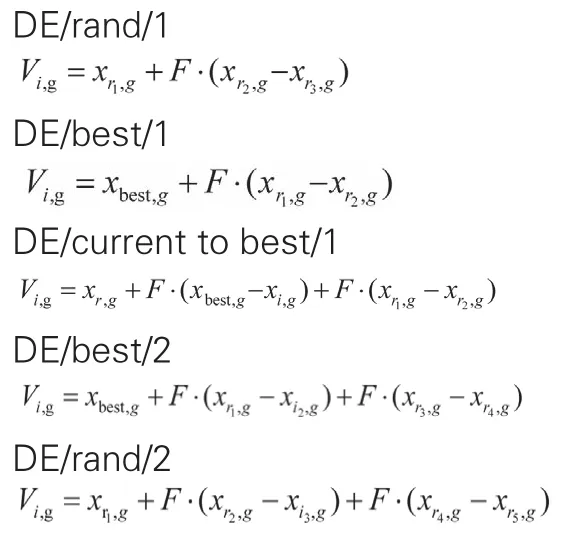
2.3 交叉
变异操作完成后,对目标向量和变异向量进行交叉操作生成试验向量,DE算法有两种交叉方式:二项式交叉(用bin表示)和指数交叉(用exp表示)。以二项式交叉具体说明如下:
通过随机选择,使试验向量至少有一个分量由变异向量贡献。二项式交叉操作的方程为:

2.4 选择

3 差分进化算法的改进
在各种应用领域和多次进化大赛中,差分进化算法已经展现出惊人的魅力。然而,DE算法不可避免地存在搜索停滞和早熟收敛、搜索性能对参数具有依赖性、算法在有限情况下很难保证获得全局最优解等问题,因此从多方面深入分析算法的运行机理,并提出相应的改进DE算法性能的调整策略,从而达到平衡算法的探索能力与开发能力的目的,依然是当前进化算法研究的重要领域。
3.1 控制参数调整策略的改进
DE算法的控制参数包括缩放因子F、交叉率CR以及种群规模NP。DE算法性能的优劣很大程度上取决于其控制参数的选择[4]。
1)种群规模NP:如果种群规模NP较小,算法可能收敛快,但是会导致算法早熟;相反,NP过大,可以增加种群的多样性,增加搜索到最优解的概率,但会导致计算量加大,收敛速度较慢。
2)缩放因子F:缩放因子影响对基向量的扰动程度,F较大时,扰动较大导致搜索步长的取值在一个更大的范围内,能够在更大范围内寻求有潜力的解,从而提高种群的多样性,但是削弱了算法的局部搜索能力;F较小,扰动量小,搜索范围较小,有利于进化的快速进行,提高算法的收敛速度。
3)交叉率CR:交叉率对种群的多样性具有重要的影响,决定种群中有多少个体可能被改变。CR较小时,种群中被改变的个体较少,当前种群中解的特征被较多地保留下来,有利于进化过程的稳定进行;CR较大时,会引起种群中更多个体发生改变,使种群多样性增强,有利于搜索到最优解。
Liu和Lampinen提出了一种基于模糊控制的适应差分进化算法FADE,通过模糊逻辑控制器来调节参数F和CR,仿真结果显示该算法在优化高维问题时的性能远远优于传统DE算法[5]。
Qin等提出一种新的自适应差分进化(SaDE)算法,F和CR借鉴前期产生优质解的经验进行自适应调整[6]。该算法中F的设置服从均值为0.5、标准方差为0.3的正态分布N(0.5,0.32),并应用于当前种群的每一差分向量,从而平衡整个优化过程的探索(F较大时)与开发(F较小)能力。CR的值服从均值为CRm,标准方差为Std的正态分布N(CRm, Std2)。将CRm初始化为0.5,此时Std应设置为一个很小的值保证CR的取值为[0,1],因此将Std设置为0.1。SaDE算法中的自适应机制中也涉及参数的调节,如正态分布的标准方差。算法中对问题不太敏感的参数代替敏感度较高的参数,因此自适应DE算法能够获得比传统DE算法更好的性能。
Zhang和Sanderson[7]提出一种新的适应差分进化算法(JADE)。在JADE算法中,对每个个体,分别应用标准正态分布和柯西分布采样确定交叉概率CR和缩放因子F。
3.2 操作算子策略的改进
除基本DE所介绍的5个变异策略外,研究人员对其他一些变异策略进行了研究。
Fan和Lampinen提出三角变异策略[8]:


该算法利用随机选择的三个个体中最好个体信息,引导试验向量向其靠近,该方法可视为一种局部搜索策略。为了进一步在收敛速度和搜索能力之间寻求一种平衡,算法使用一个概率来控制三角变异算子的使用频率。
Zhang和Sanderson提出DE/current-to-pbest策略[7],即JADE:

Liang等[9]提出利用适应度欧式距离比值改进算法的性能,用于优化多模函数问题。
3.3 混合差分进化算法
混合技术是指将两个或多个算法的优点结合在一起,在特定问题求解范围内,形成一种新的算法,近年来正成为优化算法的研究热点。研究者对DE与其他算法相混合的技术进行了大量的研究,包括与其他智能优化算法以及局部搜索方法的融合。
与D E相混合的智能优化算法有粒子群优化(PSO)、蚁群算法(ACO)、人工免疫算法(AIS)、模拟退火(SA)等。其中,DE与PSO混合的研究最多,Hendtlass首次将DE与PSO进行融合,提出当后代获得较好的适应值时更新粒子的位置,DE算法在指定的间隔对粒子群进行作用。Xin等对PSO与DE相混合进行了详尽的分析和总结[10]。Capanio等在DE框架中将PSO和另外两种局部搜索算法相结合,利用PSO在初始阶段快速改善具有较差适值的解,并将其包含在DE种群中,使这些解引导DE搜索,两种搜索方式按一定概率与DE算法相结合[11]。文献[12]提出基于一种新的混合差分粒子群启发式优化算法的电子商务物流配送优化方案。
4 总结与展望
DE算法的提出最初是为了解决连续领域的优化问题,作为智能优化技术的一个重要的分子,DE算法已经引起优化计算领域研究人员的普遍关注。目前DE算法已经广泛地应用于许多领域,在算法改进和应用上得到了快速的发展,成为进化计算领域新的研究热点。但DE算法在其理论分析,算法改进和应用研究等方面仍有广阔的值得挖掘的研究空间,需要加强并进行深入研究。加强理论方面的研究,为其改进和实际应用提供依据,这非常具有挑战性和吸引力,在这方面还需要做大量的研究。DE算法的改进研究,它包括对其控制参数(种群规模NP、缩放因子F和交叉率CR)的研究,算子(差分变异、交叉率和选择)以及种群拓扑结构等的研究,从平衡算法的探索与开发能力的角度出发,考虑种群多样性以及个体适应值在算法运行过程中的变化情况,引入适应性调节机制,提出高效稳健的协调方法,仍是DE算法的重要研究内容。
[1]Price K,Storn R,Lampinen J.Differential Evolution:A Practical Approach to Global Optimization [M].New York: Springer-Verlag, 2005.
[2]吴志峰.差异演化算法及其应用研究[D].北京:北京交通大学,2009.
[3]张航,王伟,郑玲等.一种基于密度聚类的小生境差分进化算法[J].计算机工程与应用,2008,44(23):42-45.
[4]Mandal K K, Chakraborty N.Parameter study of differential evolution based optimal scheduling of hydrothermal systems [J].Journal of Hydroenvironment Research,2012,7(1):72-80.
[5]Liu J, LampinenJ.A fuzzy adaptive differential evolution algorithm[J].Soft Computing,2005,9(6):448-462.
[6]Qin.K,Huang VL,Suganthan P N.Differential evolution algorithm with strategy adaptation for global numerical optimization [J].IEEE Transactions on Evolutionary Computation, 2009,13(2):398-417.
[7]Zhang J Q, Sanderson A C.JADE:adaptive differential evolution with optional external archive[J].IEEE Transactions on Evolutionary Computation,2009,13(5):945-958.
[8]H.Y.Fan and J.Lampinen.A trigonometric mutation operation to differential evolution[J].Journal of Global Optimization,2003,27(1):l05-129.
[9]Liang J J,Qu B Y,Mao X B,et al.Differential evolution based on fitness Euclidean-distance ratio for multimodal optimization[J].Neurocomputing,2014,137(5):252-260.
[10]Xin B,Chen J,Zhang J,et al.Hybridizing differential evolution and particle swarm optimization to design powerful optimizers: A review and taxonomy[J].IEEE Transactions on systems, Man & Cybernetics Part C,2012, 42(5):744-767.
[11]Caponio A,Neri F,Tirronen V.Super-fit control adaptation in memetic differential evolution frameworks[J].Soft Computing,2009,13(8):811-831.
[12]沈济南,梁芳,郑明辉.一种新的混合差分粒子群优化算法及其应用[J].四川大学学报(工程科学版),2014.46(6):38-43.
李斌(1974—),男(回族),河南建筑职业技术学院,高级讲师,电气、物理方向
2017-08-23
