一例三重积分多种解法的比较分析

2017-11-01张海燕李耀红李冬楠

宿州学院学报 2017年8期

关键词：张海燕柱面宿州

张海燕，李耀红，李冬楠

宿州学院数学与统计学院，宿州，234000

一例三重积分多种解法的比较分析

张海燕，李耀红，李冬楠

宿州学院数学与统计学院，宿州，234000

通过一例三重积分在直角坐标、柱面坐标和球坐标下五种解法，探讨了三重积分计算问题的基本思路和方法。结合相关文献，分析了三重积分计算中如何根据积分区域、被积函数、积分限和区域图形情况选择合适的坐标系，将三重积分化为三次积分进行计算。

三重积分；积分区域；多种解法

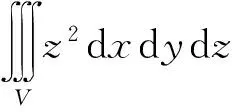
1 直角坐标系下的计算

1.1 利用截面法

由于被积函数为z2，只含有一个变量，因此可以把三重积分化为“先二重后一重”的累次积分。又由于空间区域V用平行于xy平面的平面截得的是一个圆面，即

此时积分区域V=V1+V2,其中

从而

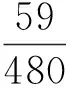
1.2 利用投影法

V={(x,y,z)|(x,y)∈D,

从而

-3r(t2-t)]dt

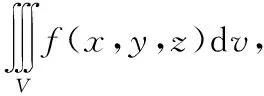
2 柱面坐标系下的计算

由于积分区域V由x2+y2+z2≤r2和x2+y2+z2≤2rz所确定，且有

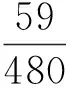
注2：通过对比，柱面坐标下计算三重积分和直角坐标系下利用投影法计算三重积分基本相同。

3 球坐标系下的计算

3.1 利用积分区域可加性

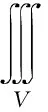
作球面坐标变换x=ρsinφcosθ,y=ρsinφsinθ,z=ρcosφ,则积分区域V1变为

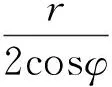
则积分区域V2变为S1和S2：

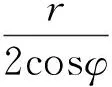
因此利用球面坐标，有

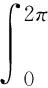
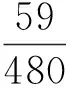
3.2 利用积分区域补全法

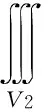
作球坐标变换x=ρsinφcosθ,y=ρsinφsinθ,z=ρcosφ,则积分区域V2变为

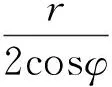
因此利用球坐标，有

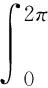
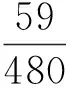
对积分区域V2也可以利用区域补全法，可以得到和以上类似的结果。

注3：比较上述两种算法，难易程度相当，说明在区域划分没有减少的情况下，利用区域可加性和区域补全法计算三重积分均可。

4 计算方法的比较分析

通过对一例三重积分的五种算法比较可知，三重积分计算基本思路和方法是选取不同坐标系，将三重积分化为三次积分，根据具体问题的特点采取不同积分次序进行计算。结合实例，三重积分计算除了一些技巧性问题外，还应注意分析以下问题：

(1)坐标系的选择。应该了解三种坐标系下积分公式的主要特点,在给定的积分区域下选用哪种坐标系更为方便。对于平面围成的积分区域,一般选用直角坐标系；对于圆锥面、旋转抛物面围成的区域或积分区域与绕z 轴旋转形成的旋转体有关时，一般选用柱面坐标系；而与球相关的积分区域，往往选取球坐标系。

(2)被积函数的特点。结合被积函数的特点选择合适的坐标系，往往能简化三重积分计算。对于被积函数中只含有一个变量的，可以选取直角坐标系，且若截面面积易求，可利用截面法求积分，如解法一；若被积函数含有两个变量，且有平方和形式，如x2+y2，则可选取柱面坐标系；若被积函数含有三个变量平方和形式，一般利用球坐标系。

(3)积分限的选择。积分限和坐标系的选取息息相关，一旦确定坐标系后，积分限一般有固定模式。因此，坐标系的选择除要关注积分区域形式和被积函数特点外，还要关注积分限是否容易确定，累次积分是否容易计算，选择不同积分限计算繁简程度不同。在具体积分限确定时，关键是看线：直角坐标和柱面坐标是看投影面的垂线与积分区域相交情况；球坐标看极点出发的射线与区域相交情况。

如本文中的例子，从积分区域形式看，选择球坐标比较合适，从被积函数看直角坐标比较合适，通过对比积分限，显然利用直角坐标计算要容易。应了解化成三次积分与化成一次积分和一个二重积分的公式的主要特点,以及给定积分区域与被积函数下使用何种公式合适。

(4)积分区域示意图的勾勒。对于由方程组或不等式给出的积分区域,尽量画出示意图，可以直观地从区域图形特点判断利用何种坐标系计算，以及如何确定积分限。

[1]费时龙.计算三重积分的一种特殊方法[J].安庆师范学院学报：自然科学版,2013,19(1):101-103

[2]陈浩.一例三重积分的解法剖析[J].宿州学院学报,2010,25(8):103-107

[3]同济大学应用数学系.高等数学[M].5版.北京:高等教育出版社,2010:99-106

[4]吕中学.关于三重积分的计算[J].高等数学研究,2016,19(2):48-50

[5]赵侠,杨路.例谈高等数学学习方法:一道习题玩转三重积分[J].湖南理工学院学报：自然科学版,2016,29(3):84-87

[6]华东师范大学数学系.数学分析[M].4版.北京:高等教育出版社,2010:264-265

10.3969/j.issn.1673-2006.2017.08.024

O172.2

1673-2006(2017)06-0097-03

2017-01-12