基于分形理论探究碳酸盐岩CT图像二值化最佳阈值

2017-11-01吴国铭李熙喆高树生刘华勋吴国铨安为国

石油地球物理勘探 2017年5期

关键词：分维二值分形

吴国铭李熙喆高树生刘华勋吴国铨安为国

(①中国科学院大学渗流流体力学研究所，河北廊坊 065007； ②中国石油勘探开发研究院廊坊分院，河北廊坊 065007； ③兰州工业学院电气工程学院，甘肃兰州 730050)

基于分形理论探究碳酸盐岩CT图像二值化最佳阈值

吴国铭*①李熙喆②高树生②刘华勋②吴国铨③安为国②

吴国铭，李熙喆，高树生，刘华勋，吴国铨，安为国.基于分形理论探究碳酸盐岩CT图像二值化最佳阈值.石油地球物理勘探，2017,52(5):1025-1032.

CT扫描构建数字岩心的一个重要环节是灰度图像的二值化。本文基于图像处理分析和分形理论计算孔渗参数，为CT图像二值化提供了更准确、更适用的约束条件。孔洞型碳酸盐岩不同形态和尺度的微观孔隙累积数量与半径分布遵循幂律关系，具有统计意义上的分形特征，且分维值与孔隙度之间存在非线性定量关系。通过自定义四连通像素值梯度突变算法与分形理论相结合的方法，统计分析了孔隙形态、数量等参数并计算了孔隙度，其平均误差小于7.2%；改进“先二值化后边缘识别”的常规方法，运用滤波降噪和边缘识别算子识别标定CT灰度图像微观孔隙，既保证了精度又提高了效率。根据这两种图像处理技术可确定最佳灰度阈值，实现CT图像二值化。该方法处理的二值图像较好地保留了不同尺度微观孔隙结构的形态和分布特征，因此可广泛应用于常规岩心重构及后续的三维数字岩心的构建。

碳酸盐岩微观孔隙 CT图像分形孔隙度最佳阈值

1 引言

分形理论的基本思想是客观事物具有自相似的层次结构，局部与整体在形态、功能、信息、时间和空间等方面完全相同或具有统计意义上的相似性[1-3]。定量刻画这种自相似结构复杂程度的参数是分数维[4]。分形理论在石油工业领域取得了一系列的成果及应用[5-10]。碳酸盐岩油气藏储层缝、洞发育[11-13]，非均质性强，研究表明裂缝和孔洞等孔隙结构具有自相似性[14-16]，如何准确获取分维值成为关键。通过岩心CT扫描图像分析微观孔隙结构的分维值得到了业界的关注，文献[17-20]基于计盒维数法分析计算CT灰度图像和二值化图像不同孔隙结构的分维值，但未见针对所得结果进一步的推广应用。将分维值与图像处理技术相结合，确定最佳二值阈值，实现图像孔隙与固相最优分割，目前尚未看到相关文献。

数字岩心可用于研究多孔介质内部微观孔隙结构及流动规律，能从微观角度揭示油气储集和渗流机理，获取储层宏观参数，为油气藏高效开发提供有力的技术指导[21-25]。CT成像技术是一种构建三维数字岩心的重要方法，通过对岩心样品不同断层X射线衰减程度的测量生成连续的反映微观孔隙信息的断面图像，并将处理后的二维图像叠加形成三维数字岩心。CT扫描图像的合理分割可对数字岩心准确性产生重要影响，在图像二值化处理中如何准确分割固相与孔隙，取决于分割阈值的合理确定。最大间距法、分水岭算法和神经网络等均可实现图像二值分割，区分固相与孔隙，但上述方法仅针对灰度信息进行处理，未考虑图像所含的物理信息，如孔隙度等，导致分割结果与实际存在偏差。虽然以实测孔隙度为约束条件确定的分割阈值能更准确地反映储层微观孔隙特征[26-27]，但对于形状不规则的岩心样品，往往无法通过实验获取其孔隙度，给二值阈值的确定带来不便，本文基于分形理论，通过对部分图像的预处理，获取微观孔隙的分维数，最终得到理论孔隙度作为分割阈值的约束条件，为CT图像的二值化处理提供新的方法和思路。

2 分维值与孔隙度相关性分析

碳酸盐岩固体颗粒级配良好，直径λ跨度范围约为三个量级，且连续分布，如从若干微米到若干毫米，具有统计自相似性和标度不变性[28]，伴生的孔洞满足累积数量与直径分布的幂律关系，为分形多孔介质。

根据分形理论，在d维欧式空间中的分形体的某个测量物理量满足[21]

(1)

式中：F(γ)为待测物理量；L0为参考线性常数；γ为测量线性尺度；d为欧式空间维数；D为分形维数。

在无标度区间内，多孔介质单位体积中半径大于λ的孔隙累积数与半径分布满足

Nc(λ≤L)=Aλ-D

(2)

式中：Nc为单位体积中半径大于λ的孔隙累积数；λ为孔隙半径；L为测量尺度；A为比例系数。对式(2)中的λ求微分，可得单位体积分形多孔介质中孔隙半径的概率密度函数

(3)

推导出孔隙度[21,22]与分形维数的关系式为

(4)

式中：φ为孔隙度；λmax为孔隙最大半径；λmin为孔隙最小半径。

综合式(3)、式(4)可得[29]

(5)

若已知多孔介质单位体积孔隙数量N、孔隙最大半径λmax和最小半径λmin、分维值D，即可计算出岩心孔隙度φ。

3 CT图像处理分析

3.1 CT成像技术简述

X射线CT是一种借助于计算机将X射线断层扫描的断面重现出来的成像技术，可实现非透明物体组成及结构的无损检测，当强度均匀的射线束透照射物体时，由于内部不同组分的密度、结构等的差异，使不同部位透射射线强度不同，能量衰减程度满足比尔定律

(6)

式中：I0、I分别为X射线穿过物体前、后的能量；μi、Li分别为第i种组分的衰减系数和透射路径长度。

X-CT机的基本结构包括：X射线源、样品夹持器和X射线检测器(图1)。X射线源发射X射线，经由载物台上的样品(保持旋转状态)吸收后，由X射线检测器接收衰减后的信号并传送给计算机，最后输出样品扫描图像。

图1 X射线CT原理图

选取4块碳酸盐岩储层岩心(基本物性参数见表1)进行CT扫描(纵向扫描间隔为0.076mm)，每块岩心得到1300余张图像(图2)，每块岩心等间隔选取400张图像作为预处理对象，计算其分维值和孔隙度，从而确定最佳分割阈值。

表1 岩心物性参数表

图2 岩心原始CT图像

3.2 盒维数法确定分维值

本次实验中岩心扫描后得到的原始CT图像为RGB模式，为便于运用计盒维数法确定微观孔隙结构分维值，将RGB图像转换为像素值为0～255的灰度图像(图像大小不变，像素点总数仍为990×990)，可通过灰度值表征扫描区域的不同组分、结构等信息，如固相颜色较浅、灰度值较大，微观孔隙颜色较深、灰度值较小。

CT灰度图像中，灰度值可视为沿Z轴方向高度为z的微小长方柱体，这样，扫描区域的灰度值具有高低起伏的空间形态(图3)，每个像素点的自由度为3(指平面坐标x、y和灰度值z)。

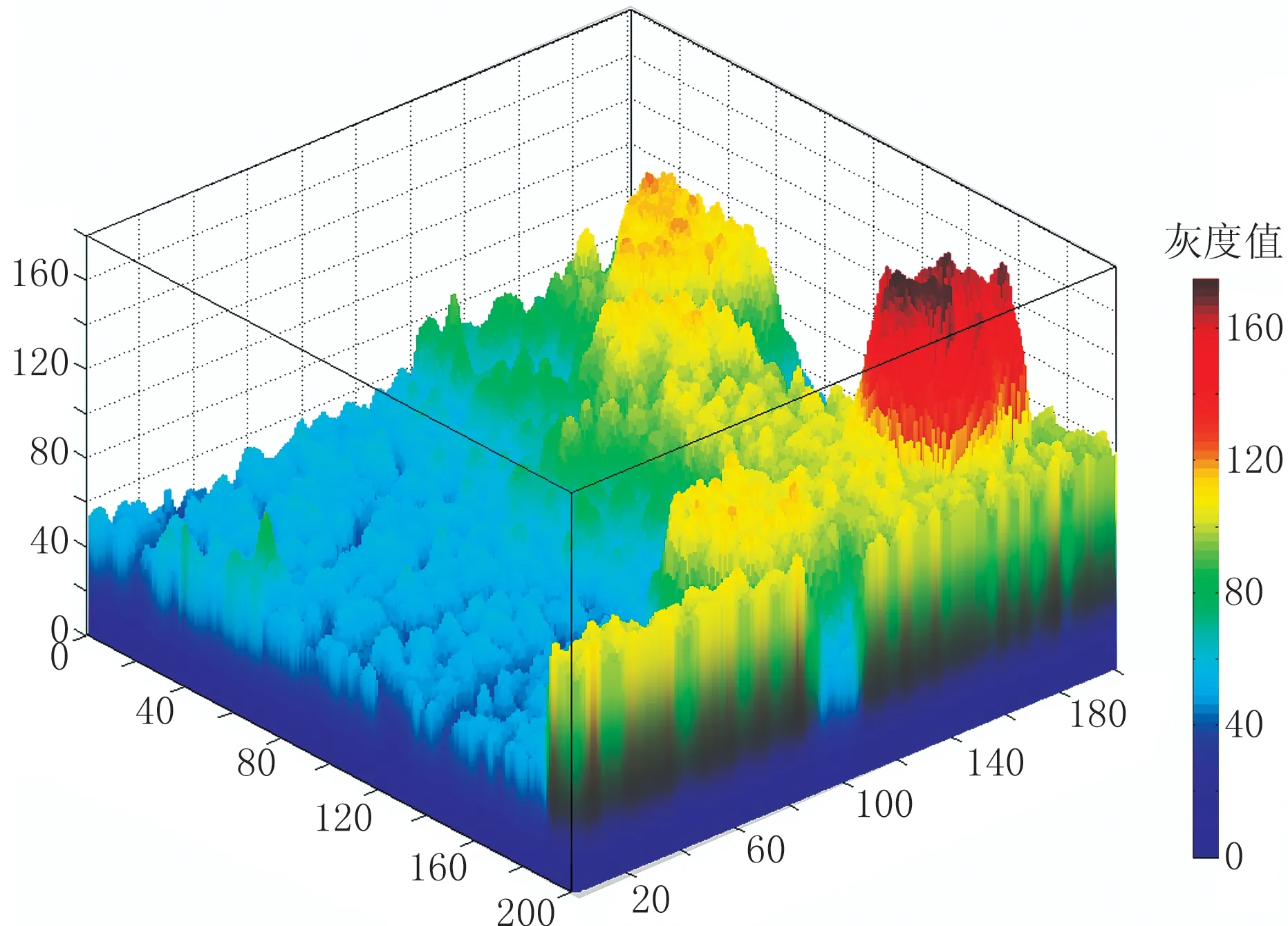
图3 CT图像中各像素点的灰度值柱状分布图(局部)

针对由一系列微小长方柱体构成的灰度空间，采用计盒维数法确定微观孔隙结构分维值[17]，其基本原理如下：用高度为hi的微小长方柱体(盒子)度量起伏不定的灰度空间，如某点灰度值为zi，所需盒子的数量为

(7)

(8)

图关系曲线

基于1号岩心400张预处理灰度图像得到的400个分维值D分布情况如图6所示，可知分维值D分布在(1.6411，1.6507)范围内，沿岩心轴向分布的波动性较小。

图曲线线性部分

图6 分维值沿岩心轴向分布

综合400张预处理图像，得到平均分维值，见表2。分维值大小可表征微观孔隙发育程度及非均质性强弱，分维值分布与岩心特征相吻合。如1、3号岩心孔洞、裂缝较发育，非均质性较强，其平均分维值较大； 2号岩心部分发育裂缝，其平均分维值次之； 4号岩心孔隙相对不发育，其平均分维值最小。

3.3 微观孔隙结构边缘提取

为获取单位体积多孔介质中的微观孔隙总数N，需准确识别灰度图中微观孔隙结构边缘，统计每张图像中单连通孔隙数量。

在边缘检测前，运用邻域大小为3×3的中值滤波器[31]对灰度图像进行降噪处理，可在不改变微观孔隙与固相对比度的前提下，有效地提高边缘检测精度。

在灰度图像中，边缘是指研究对象的边界，即反映灰度值剧烈变化的曲线，边缘检测的目的就是寻找这些灰度值剧烈变化的像素点，可通过MATLAB的edge函数实现灰度图中微观孔隙结构边缘的有效检测。edge函数边缘检测方法的优点在于使用了两种不同的阈值分别检测强边缘和弱边缘，只有在强、弱边缘相连时，输出图像中才包含弱边缘，真正的弱边缘易于检测，且有效避免了噪声填充。edge函数求取边界的算子较多，如sobel、prewitt、log、roberts和zeroscross等，本次实验运用canny算子完成边界检测。

BS-240VET全自动生化分析仪（深圳迈瑞生物医疗电子股份有限公司）；Bio-Rad D-10 HbA1C分析仪（美国Bio-Rad公司）；α1-微球蛋白（α1-MG）试剂盒（德灵公司）；血清尿清蛋白/尿肌酐（UALB/Cr）、视黄醇结合蛋白（RBP）、血清胱抑素-C（Cys-C）（南京威科特曼公司产品）；同型半胱氨酸（Hcy）、尿β2微球蛋白（U-β2-MG）试剂盒（宁波瑞源生物科技有限公司）；糖化血红蛋白（HbA1C）试剂盒（美国Bio-Rad公司）。C-反应蛋白（CRP）（宁波美康生物科技股份有限公司）。

canny算子是一种较新的边缘检测算子，具有较高的边缘检测性能，得到了越来越广泛的应用。canny算子边缘检测的基本原理如下： ①求取高斯滤波器f与图像函数g(x，y)的卷积(式9)； ②计算图像梯度的幅值和方向； ③对梯度图像应用非极大值抑制，确定梯度局部最大值

(9)

对于canny算子更深入的理论解析不做赘述，详细推导过程可参考文献[33]。

图7展示了运用edge函数的canny算子提取得到的灰度图像中微观孔隙结构的边缘信息，将原始灰度图像中绝大部分孔隙结构包含在内(其余更微小的孔隙结构限于图像分辨率无法表征)，实现了单连通孔隙的有效识别与准确划分。

图8所示为1号岩心每张预处理图像(共计400张)中微观孔隙数量沿岩心轴向分布特征，溶蚀段孔隙密集发育，从图像中识别出的微观孔隙数量较多；致密段孔隙稀疏分布，从图像中识别出的微观孔隙数量较少，单张图像最大的孔隙数量可达最小值的3倍之多，体现了碳酸盐岩较强的非均质性。获取孔隙数量后，可进一步计算得到单位体积多孔介质中的孔隙总数N(见表2)。

3.4 微观孔隙结构参数计算

由图7b可知，canny算子输出图像为二值图像，孔隙边界点为1，其余点均为0。针对该二值图像，采用自定义4连通像素值梯度突变算法，自主编程实现单连通孔隙结构参数(如面积)的计算，自定义像素值梯度计算公式为

=f(i,j+1)-f(i,j)

(10)

式中：i、j为像素点坐标；f为像素值。在二值图中，固相和孔隙相中的像素值梯度均为0，而在两相边界处像素值梯度出现突变，为±1。

图7 canny算子边缘识别效果图

图8 微观孔隙数量沿岩心轴向分布特征

遍历二值图像矩阵，若第i行第j列的像素值为0，则自第j列始逐列计算像素值梯度; 若出现突变，确定第i行的左右边界，第i行也是该单联通孔隙相的上边界。

判断第i行第j列的左边界点下方(第i+1行第j列)像素值： ①若为0，则以第i+1行第j列像素点为始，分别向左、向右计算不同列的像素值梯度，通过突变确定第i+1行的左右边界； ②若为1，则判断第i行第j+1列像素点下方(第i+1行第j+1列)像素值。重复上述过程，确定第i+1行的左右边界。

如果循环至第n行，0值下方均为1，可确定第n行为该单联通孔隙相的下边界，循环结束。这样即可找到一个完整的单连通孔隙区域，并对其所含全部像素点及边界点分别标记。

运用上述算法，可准确计算单张二值图像相互独立的微观孔隙结构面积(即所含像素点总数量)。但由于真实孔隙的位置、形态、大小等复杂多样，难以获其特征参数，可将各孔隙视为与其等面积的圆，进而计算其等效半径λ。表2为统计不同岩心预处理图像得到的微观孔隙等效半径最大值λmax和最小值λmin。图9为孔隙等效半径分布特征，最大等效半径约为80像素点，即5.976mm，最小等效半径约为2像素点，即0.156mm，表明孔隙形态、位置和大小差异性较大，具有较强的非均质性；同时，较好地实现了微小孔隙的识别和标定，程序稳定性和准确性较好。

图9 孔隙等效半径沿岩心轴向分布特征

由表2可知，对于缝洞型碳酸盐岩储层，普遍发育横截面积较大的孔隙，如1号岩心的孔隙最大等效半径为5.976mm，具有较好的储集特性，分析CT图像得到的认识与常规物性实验结果相一致，充分体现了可视化方法的直观性和准确性。

上述所有过程均由自编的MATLAB程序自动批量处理并输出计算结果。

表2 计算孔隙度所需各参数值

3.5 确定孔隙度和最佳分割阈值

经过前述分析计算，已经获取了微观孔隙平均分维值D、单位体积多孔介质中的孔隙总数N和孔隙等效半径λmax、λmin。现在，将各参数代入式(6)，即可得到岩心孔隙度(表3)，计算所得孔隙度和实验孔隙度相近，最大相对误差为8.7%，表明基于理论公式计算的孔隙度精度较高，符合储层实际，该孔隙度可作为CT灰度图像二值分割的约束条件，特别是针对未开展常规孔隙度测试的岩心，其CT图像二值分割最佳阈值满足[32]

f(k*)

(11)

式中：Imin、Imax分别为CT图像最小和最大灰度值；P(i)为像素点i的灰度值；φ为计算孔隙度；k*为最佳阈值。

将得到的计算孔隙度代入式(11)，确定的最佳分割阈值见表3，分割后的二值图像如图10所示，较好地保留了不同尺度微观孔隙结构的形态和分布特征，为后续构建三维数字岩心奠定坚实基础。

从理论上来说，同一储层段的岩心样品CT图像应取相同的最佳阈值，但由表3可知，4块岩心对应的最佳阈值并不相同，而是存在微小差异。逐次选取表3中的一个最佳阈值，对4块岩心CT图像开展相同阈值下的二值分割，统计孔隙度相对误差，结果如图11所示。

表3 孔隙度及相对误差和最佳阈值

图10 最佳阈值确定的二值图像

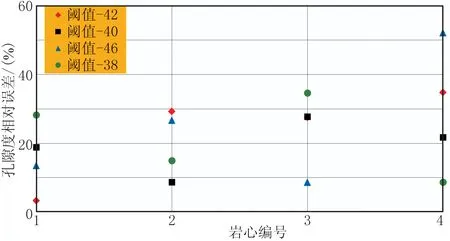
图11 不同阈值对应的孔隙度相对误差

由图11可知，采用相同阈值对CT图像分割后，4块岩心所得孔隙度相对误差差异较为明显，不适宜对同一储层段的岩心样品的CT扫描图像采用完全相同的阈值开展二值分割。上述结果可能是由于不同岩心样品中矿物成分及颗粒胶结程度的差异与CT扫描中的噪声干扰等所导致。

4 结论与认识

本文基于缝洞型碳酸盐岩CT图像分析处理，探究了微观孔隙结构分形特征和图像二值分割最佳阈值的确定，主要结论如下。

(1)CT扫描技术能实现不同尺度微观孔隙结构的可视化表征，为研究多孔介质内部孔隙网络和数字岩心的构建提供了条件。

(2)碳酸盐岩储层属于固相分形多孔介质，其中伴生的缝洞等微观孔隙结构满足累积数量与半径分布的幂律关系，即具有统计意义上的分形特征；分维值大小可表征微观孔隙发育程度及非均质性强弱，微观孔隙等效半径范围越大，结构越复杂，分维值越大，且分维值与孔隙度之间存在非线性定量关系。

(3)对灰度图像的适当降噪处理及边缘识别算子的合理运用，可实现对灰度图像微观孔隙的有效标识，有别于先二值化后边缘识别的常规方法，在保证精度的同时提高了效率；自定义4连通像素值梯度突变算法可有效统计微观孔隙结构参数，准确获取孔隙最大和最小等效半径。

(4)分维值等参数计算所得孔隙度与实验孔隙度的相对误差较小，表明通过理论公式所得孔隙度精度较高，可作为确定二值分割最佳阈值的约束条件，以此所得的二值图像中较好地保留了不同尺度微观孔隙结构的形态和分布特征，为后续构建三维数字岩心奠定了坚实基础。

(5)本文为探究实验孔隙度未知的岩心CT图像如何实现准确的二值化处理提供了新的角度和方法。

[1] Mandelbrot B B.The Fractal Geometry of Nature.Freeman San Francisco，1983.

[2] 翟云芳.渗流力学.北京：石油工业出版社，2009，152-156. Zhai Yunfang.Seepage Flow Mechanics.Petroleum Industry Press，Beijing，2009，152-156.

[3] 聂笃宪.随机分形裂缝模型的研究[学位论文].广东广州：广东工业大学，2005. Nie Duxian.Study of Random Fractal Fracture Model [D].Guangzhou University of Technology，Guangzhou，Guangdong,2005.

[4] 郑红军.裂缝性储集层的分形分维应用研究[学位论文].四川成都：西南石油大学，2003，2-12. Zheng Hongjun.Application of fractal dimension of fractured reservoirs [D].Southwest Petroleum University，Chengdu，Sichuan,2003，2-12.

[5] 施泽进，罗蛰潭，彭大钧等.油气藏体积分布的分形特征及其意义.大地构造与成矿学，1995，19(1)：71-72. Shi Zejin，Luo Zhetan，Peng Dajun et al.Fractal pro-perty of size distributions of oil-gas deposites.Geotectonica et Metallogenia，1995，19(1)：71-72.

[6] 潘葆芝，薛林福.分数维及其在测井地质解释中的应用.测井技术，1992，16(3)：215-217. Pan Baozhi，Xue Linfu.Fractal dimension and its application to geologic interpretation of log data.Well Logging Technology，1992，16(3)：215-217.

[7] 郑继明.分形和小波变换在油气预测中的应用.预测，1996，(6)：51-52. Zheng Jiming.Fractal and wavelet transform in application of oil-gas prediction.Forecasting，1996，(6)：51-52.

[8] 隋少强，宋丽红，李淑敏.分形理论在储集层横向预测和油气层判断中的应用.新疆石油地质，2001，22(4)：342-343. Sui Shaoqiang，Song Lihong，Li Shumin.The application of fractal theory in lateral prediction of reservoir and hydrocarbon diagenesis.Xinjiang Petroleum Geo-logy，2001，22(4)：342-343.

[9] 蒋加钰，段玉顺.分形理论在油气检测中的应用.石油物探，1995，34(1)：49-50. Jiang Jiayu，Duan Yushun.Application of fractal theory to hydrocarbon detection.GPP，1995，34(1)：49-50.

[10] 李春华，鲁港，毛俊莉等.分形理论在井间薄储集层描述中的应用.石油学报，1998，19(4)：27-28. Li Chunhua，Lu Gang，Mao Junli et al.Application of fractal theory in the inter-well thin reservoir description.Acta Petrolei Sinica，1998，19(4)：27-28.

[11] 杨柳，沈亚，管俊亚等.多维数据裂缝检测技术探索及应用.石油地球物理勘探，2016，51(增刊1)：58-61. Yang Liu，Shen Ya，Guan Junya et al.Fracture detection based on multi-dimension data.OGP，2016，51(S1)：58-61.

[12] 吉学林.碳酸盐岩裂缝型储层预测.石油地球物理勘探，2013，48(增刊1)：95-98. Ji Xuelin.The characterization of fractures in carbo-nate reservoirs by full azimuth seismic data.OGP，2013，48(S1)：95-98.

[13] 凌云，高军，孙德胜等.裂缝储层的地震预测技术与应用实例.石油地球物理勘探，2015，50(1)：92-96. Lin Yun，Gao Jun，Sun Desheng et al.A case study of fractured reservoir prediction.OGP，2015，50(1)：92-96.

[14] 文慧俭，闫林，姜福聪等.低孔低渗储层孔隙结构分形特征.大庆石油学院学报，2007，31(1)：16-18. Wen Huijian，Yan Lin，Jiang Fucong et al.Fractal property of low porosity and permeability reservoirs’ pore structure.Journal of Daqing Petroleum Institute，2007，31(1)：16-18.

[15] 王自明，宋文杰，戴勇等.利用分形模拟建立裂缝型碳酸盐岩储层渗透率变异函.天然气工业，2007，27(11)：73-74. Wang Ziming，Song Wenjie，Dai Yong et al.Application of fractal simulation technique to modeling of fractured carbonate reservoir.Natural Gas Industry，2007，27(11)：73-74.

[16] 邓攀，陈孟晋，杨泳.分形方法对裂缝性储集层的定量预测研究和评价.大庆石油地质与开发，2006，25(2)：19-20. Deng Pan，Chen Mengjin，Yang Yong.The application of fractal approach to the quantitative estimation research and evaluation of fractured reservoir.Petroleum Geology and Oilfield Development in Daqing，2006，25(2)：19-20.

[17] 彭瑞东，杨彦从，鞠杨等.基于灰度CT图像的岩石孔隙分形维数计算.中国科学，2011，56(26)：2258-2264. Peng Ruidong，Yang Yancong，Ju Yang et al.Fractal dimension of pore structure based on gray CT images.Science China Press，2011，56(26)：2258-2264.

[18] 何娟，刘建立，吕菲.基于CT数字图像的土壤孔隙分形特征研究.土壤，2008，40(4)：663-665. He Juan，Liu Jianli，Lv Fei.Characterizing fractal characteristics of soil pores based on high-resolution digital CT images.Soils，2008，40(4)：663-665.

[19] 冯杰，于纪玉.利用CT扫描技术确定土壤大孔隙分形维数.灌溉排水学报，2005，24(4)： 27-28. Feng Jie，Yu Jiyu.Determination fractal dimension of soil macropore using computed tomography.Journal of Irrigation and Drainage， 2005， 24(4)： 27-28.

[20] 陈学松，吴爱祥，杨保华等.基于CT图像法的砂岩散体孔隙结构分形特征研究.金属矿山，2007，37(10)：75-76. Cheng Xuesong，Wu Aixiang，Yang Baohua et al.Study on fractal characteristics of pore structure of bulk rock-ore in dump learching based on CT image.Metal Mine，2007，37(10)：75-76.

[21] 王金波.岩石孔隙结构三维重构及微细观渗流的数值模拟研究[学位论文].北京：中国矿业大学(北京)，2014，2-6. Wang Jinbo.3D Reconstruction of Porous Rock and Numerical Simulations of Fluid Flow at Mesoscale Levels [D].China University of Mining and Technology (Beijing)，Beijing,2014，2-6.

[22] 聂昕.页岩气储层岩石数字岩心建模及导电性数值模拟研究[学位论文].北京：中国地质大学(北京)，2014，19-24. Nie Xin.Digital Core Modeling and Numerical Study of Electrical Conductivity of Shale Gas Reservoir Rock [D].China University of Geosciences(Beijing)，Beijing,2014，19-24.

[23] 刘学峰.基于数字岩心的岩石声电特性微观数值模拟研究[学位论文].山东青岛：中国石油大学(华东)，2010，2-20. Liu Xuefeng.Numerical Simulation of Elastic and Electrical Properties of Rock Based on Digital Cores [D].China University of Petroleum (East China)，Qingdao,Shandong,2010，2-20.

[24] 张挺.基于多点地质统计的多孔介质重构方法及实现[学位论文].安徽合肥：中国科学技术大学，2009，3-6. Zhang Ting.Research on the Reconstruction of Po-rous Media Based on Multiple-point Geostatistics [D].University of Science and Technology of China，Hefei,Anhui,2009，3-6.

[25] 赵秀才.数字岩心及孔隙网络模型重构方法研究[学位论文].山东青岛：中国石油大学(华东)，2009，18-22. Zhao Xiucai.Numerical Rock Construction and Pore Network Extraction [D].China University of Petroleum (East China)，Qingdao,Shandong,2009，18-22.

[26] 耿冲，杨永飞，高莹.不同分辨率岩石CT图像的优化处理方法.科学技术与工程，2014，14(2)：2-3. Geng Chong，Yang Yongfei，Gao Ying.Optimization of image processing method based on rock CT images of different resolutions.Science Technology and Engineering，2014，14(2)：2-3.

[27] 姜蓉蓉，肖沙里，高家利.改进分水岭算法的彩色图像分割技术.计算机工程与应用，2009，45(19)：172-173. Jiang Rongrong，Xiao Shali，Gao Jiali.Color image segmentation based on improved watershed transform.Computer Engineering and Applications，2009，45(19)：172-173.

[28] 孔祥言.高等渗流力学.安徽合肥：中国科学技术大学出版社，2010. Kong Xiangyan.Higher Seepage Mechanics.University of Science and Technology of China Press，Hefei,Anhui,2010.

[29] 刘俊亮，田长安，曾燕伟等.分形多孔介质孔隙微结构参数与渗透率的分维关系.水科学进展，2006，17(6)：813-815. Liu Junliang，Tian Chang’an，Zeng Yanwei et al.Fractal dimensionality dependence of micro structural parameters and permeability in fractal porous media.Advances in Water Science，2006，17(6)：813-815.

[30] 姜虹，范宜仁，陈华.应用分形理论计算碳酸盐岩地层胶结指数m值.测井技术， 2012， 36(3)： 251-252. Jiang Hong，Fan Yiren，Chen Hua.On calculation of cementation indexmin carbonate formation using fractal theory.Well Logging Technology，2012，36(3)：251-252.

[31] 周丽，庄众，成景旺等.利用自适应迭代多级中值滤波法分离海上多震源混合波场.石油地球物理勘探，2016，51(3)：434-436. Zhou Li，Zhuang Zhong，Cheng Jingwang et al.Multi-source blended wavefield separation for marine seismic based on an adaptive iterative multi-level median filtering.OGP，2016，51(3)：434-436.

[32] 赵秀才，姚军，房克荣.合理分割岩心微观结构图像的新方法.中国石油大学学报(自然科学版)，2009，33(1)：65-66. Zhao Xiucai，Yao Jun，Fang Kerong.A new reasonable segmentation method for microstructure image of re-servoir rock.Journal of China University of Petroleum(Edition of Natural Sciences),2009，33(1)：65-66.

[33] 张强，王正林.精通MATLAB图像处理.北京：电子工业出版社，2009. Zhang Qiang，Wang Zhenglin.Proficient MATLAB in Image Processing.Publishing House of Electronics Industry，Beijing,2009.

(本文编辑：朱汉东)