独立分量分析与压缩感知微地震弱信号提取方法
2017-11-01宋维琪李艳清
宋维琪 李艳清 刘 磊
(中国石油大学(华东)地球科学与技术学院,山东青岛 266580)
独立分量分析与压缩感知微地震弱信号提取方法
宋维琪*李艳清 刘 磊
(中国石油大学(华东)地球科学与技术学院,山东青岛 266580)
宋维琪,李艳清,刘磊.独立分量分析与压缩感知微地震弱信号提取方法.石油地球物理勘探,2017,52(5):984-989,1041.
结合独立分量分析和压缩感知理论各自的优势,提出了独立分量分析与压缩感知联合理论的微地震弱信号提取方法。从欠定盲信号分离和稀疏重构入手,通过对源信号的特征分析得到欠定盲分离模型中混合矩阵,基于该矩阵,建立欠定盲信号重构模型,采用压缩感知理论的正交匹配追踪方法和压缩采样匹配追踪方法,对源信号进行重建。对混合矩阵、正交化、稀疏化及稀疏度等核心问题进行了系统分析,实现基于独立分量分析与压缩感知微地震弱信号重建方法。实际资料处理结果验证了方法的可行性。
微地震资料 独立分量分析 压缩感知 稀疏重建 弱信号提取
1 引言
目前,对弱信号提取问题,大多是针对周期或准周期重复性信号开展的讨论。微地震信号在时间采样方向,具有局部脉冲的特点,大部分微地震信号的信噪比较低,特别是当有效信号较弱时,会完全被噪声所淹没,其信号提取就变得更为困难。前人在微地震弱信号检测方面研究了多种方法,如盲源分离法[1]、随机共振法、小波分析及自适应方法等,在微地震弱信号检测方面取得了一定的效果。在微地震弱信号提取方面笔者也曾做过研究[2],虽然取得了一些成果,但是面对复杂的微地震信号仍存在一定的不足。压缩感知理论是近几年兴起的数据压缩方法,对于提高资料的信噪比有一定的效果[3-5],但是在微地震弱信号检测方面,特别是被噪声淹没的弱信号的提取检测问题,由于难以对弱信号进行稀疏化,应用效果不甚理想。
无论是盲分离技术还是压缩感知技术,都牵涉到矩阵方程组的求解问题。迄今,对于超定和适定盲处理问题,已经提出了很多算法[6,7],但是在实际应用中,传统方法的结果一般很不理想,通常是通过独立分量分析方法[8,9](ICA方法)实现求解。而很多信号在时间域上并不具有稀疏性,必须对其进行某种特殊的线性变换,使其在变换域中具有稀疏性[10-13]。
如何找到信号的最佳稀疏表示域是压缩感知理论应用的基础,只有选择合适的稀疏基表示信号才能保证信号的稀疏度,从而保证信号的恢复精度[14-18]。在研究信号的稀疏表示时,可以通过稀疏度衡量信号稀疏表示能力。
压缩感知对信号具有较强的稀疏化能力,但是在稀疏化过程中往往疏漏了一些弱信号的成分,而独立分量分析能够把各种信号相对较全面地揭示出来[19,20],但是独立分量存在过分稠密的问题,降低了对有效信号分析的能力,因此结合两种理论的优势,提出了基于独立分量分析与稀疏重建微地震弱信号提取方法。
2 微地震盲信号压缩感知重建
假设微地震信号有N个源信号s1,s2,…,sN,写成矩阵形式S=[s1,s2,…,sN]T;M个观测信号x1,x2,…,xM,写成X=[x1,x2,…,xM]T。源信号和观测信号之间的关系可以通过一个线性算子A表示为
X=AS=A[s1,s2,…,sN]T
(1)
即
(2)
N个源信号写成一维向量形式为
S= [s1(1),s1(2),…,s1(T);s2(1),s2(2),…,s2(T);
…;sN(1),sN(2),…,sN(T)]T
(3)
M个观测信号写成一维向量形式为
X= [x1(1),x1(2),…,x1(T);x2(1),x2(2),
…,x2(T);…;xM(1),xM(2),…,xM(T)]T
(4)
式中T为微地震信号长度。
那么源信号S和观测信号X的一维向量关系可表示为
(5)
式中
(6)
式(5)就是独立变量分析中转换矩阵方程,其中E=[Eij]∈RM×T×N×T是转换矩阵或混合矩阵。
在压缩感知理论下,源信号S在一组基下可稀疏表示为
(7)
式中:Ψ=[φ1,φ2,…,φM]为基向量,α为系数向量。对于给定观测信号X和测量矩阵Φ,寻找源信号S,使
X=ΦΨα
(8)
且满足在某组稀疏基Ψ的作用下S=Ψα。在一般的压缩感知算法中要求测量矩阵Φ为已知,设计为随机矩阵的形式,而且稀疏基Ψ也已知,即在传感矩阵Θ=ΦΨ已知的前提下设计各种优化算法来估计源信号的稀疏表示α,然后通过变换S=Ψα得到源信号[21-24]。
要恢复或重建源信号,测量矩阵Φ和稀疏基矩阵Ψ的设计是关键。测量矩阵一般流行的设计方法是采用随机高斯矩阵。这种方法设计的测量矩阵,在数学上满足了其和基正交的条件,同时也满足了压缩感知的RIP条件。如果观测信号噪声成分较多,这时利用以上方法设计测试矩阵,重建源信号的效果较差。因此,采用独立变量分析方法进行测量矩阵设计,即对观测信号进行独立变量分析,建立正交的测量矩阵。
3 混合矩阵估计与稀疏化
独立分量分析中的关键问题是混合矩阵的估计,为了得到混合矩阵的最优估计,混合矩阵的正交化和稀疏化是获得混合矩阵最优估计的核心。
3.1 混合矩阵的正交化方法
对于微地震信号提取而言,矩阵的正交化涉及两方面的问题: 一是如何组成正交化矩阵; 二是对已有矩阵如何正交化。正交化的目的: ①满足算法自身的要求条件; ②得到独立的正交分量。矩阵正交化后得到的独立分量是正交的,但未必是期望的正交分量。对于微地震信号提取问题,目的是得到期望正交分量。为此,需要讨论从观测的微地震资料中如何构建正交化混合矩阵。
3.1.1 数据组合正交化
(1)去均值化处理;
(2)在微地震信号满足最小相位或准最小相位的条件下,通过频谱分析获得微地震子波主频,根据主频大小确定时窗长度;
(3)把整个时窗长度为W的微地震信号,分成P段,研究发现取P=3较合适,并且段与段之间有一定重叠;
(4)对相邻道进行分段,为了避免相邻道数据的相关问题,相邻道数据选取错开一定的时移。
3.1.2 自适应最佳独立分量个数估计
独立分量的个数就是测量矩阵的维数,测量矩阵维数的大小与稀疏度密切相关。因此,确定合适独立变量个数至关重要。
对信号进行独立分量分析处理,计算不同道的分解分量相关系数,对任意两道的L个分量两两计算相关系数,找出相关系数最大时对应的两个分量,然后对多道依此计算,找出多道相关系数最大时对应的分量[25]。如果混合矩阵的维数(分量的个数)选取不合适,就有可能提取不到有用信号。为此,设计自适应方法,自动调整计算不同维数分量的多道相关系数,当维数取得合适时,多道有用信号分量的相关系数最大,进而分离出有效弱信号。
3.2 混合矩阵的稀疏化方法
稀疏化的本质是从混合信号中辨识出混合矩阵中各列的期望方向。有的信号在当前状态下(时间序列)稀疏化(同域稀疏化)不明显,但是如果把该信号转换到其他域如频率域,稀疏化(变换域稀疏化)就明显了[26]。
线性变换后混合矩阵的形式不会发生变化,则式(1)经过变换后可以表示为
Γ[X(t)]=Γ[AS(t)]=AΓ[S(t)]
(9)
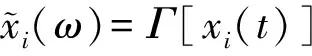
(10)
如何选取线性变换Γ(·)是问题的重点与难点。尽管短时Fourier变换可以使某些信号更加稀疏,但是由于涉及到如何选取时窗函数和时窗的宽度及重合度等问题,往往不能得到最优的表示。压缩感知对信号具有较强的稀疏化能力,但是在稀疏化过程中往往疏漏了一些弱信号的成分,而独立分量分析能把各种信号相对较全面地揭示出来,但是独立分量过度稠密降低了对有效信号分析的能力,二者结合进行信号稀疏化可取得较好的效果[27]。
图1为原始地震资料,图2为小波变换去噪处理结果,图3为独立分量分解小波去噪结果。对比图1~图3可以发现,小波变换方法在微地震资料去噪方面有一定效果,但是对一些区域性噪声压制作用有限和对高频信号的揭示能力也不够强,但独立分量对有效信号具有很好的揭示能力。对比图3a与图3b可以发现,组合矩阵正交化后能够得到独立的正交分量,可以很好地分离出有效信号、压制区域噪声,提高了微地震资料的信噪比。

图1 原始微地震资料

图2 小波变换噪声压制方法处理结果
4 信号重建的唯一性问题
决定重构源信号所需要的测量值的数目是由信号的稀疏度决定的。在给定稀疏度的前提下,一个信号可以有不同的表示方式。但是,总存在一种稀疏度最小情形,把这种情况定义为信号的最稀疏表示。显然,信号的最稀疏表示是唯一的。
研究发现,随着测量值数目的增加,恢复的信号与原信号的绝对误差越来越小,直到测量值数目大于某一特定值时,就能充分恢复原信号。显然,稀疏度越大,完全重构信号需要的测量值越多。当信号的稀疏度越大时,成功重构信号需要的测量值数目越多,而且随着测量值数目的增加,能够成功重构的信号越来越多,直到全部信号都能成功恢复,即信号成功重构的概率趋近于1。
为了进一步讨论微地震信号压缩感知重建特别是微地震弱信号重建问题,有必要引入稀疏率概念,假设信号的长度为I,稀疏度为K,则稀疏率λ表示为信号长度和稀疏度的比值,即λ=K/I。微地震反射信息不论是强信号还是弱信号都是一定长度的微地震子波和地层传播响应的综合结果,通过压缩感知方法,虽然通过变换域的方法增强了这些叠加的弱信号的稀疏性,但是如果稀疏度和稀疏率选取不合适,仍然得不到弱信号重建的真解。根据微地震子波特性,如果稀疏域是频域,则I的长度取地震子波长度的2倍(地震子波补零扩展)。图4为图1数据在不同稀疏率下的压缩感知重建结果,图5为不同稀疏率的基于独立分量分析和压缩感知的重建结果,可以发现相互耦合的弱信号和噪声通过盲分离(独立分量分析)实现了解耦,增强了对微地震信号进行稀疏化的能力。通过大量试算可知,稀疏率取0.1~0.2较为合适。

图3 独立变量分析方法噪声压制结果
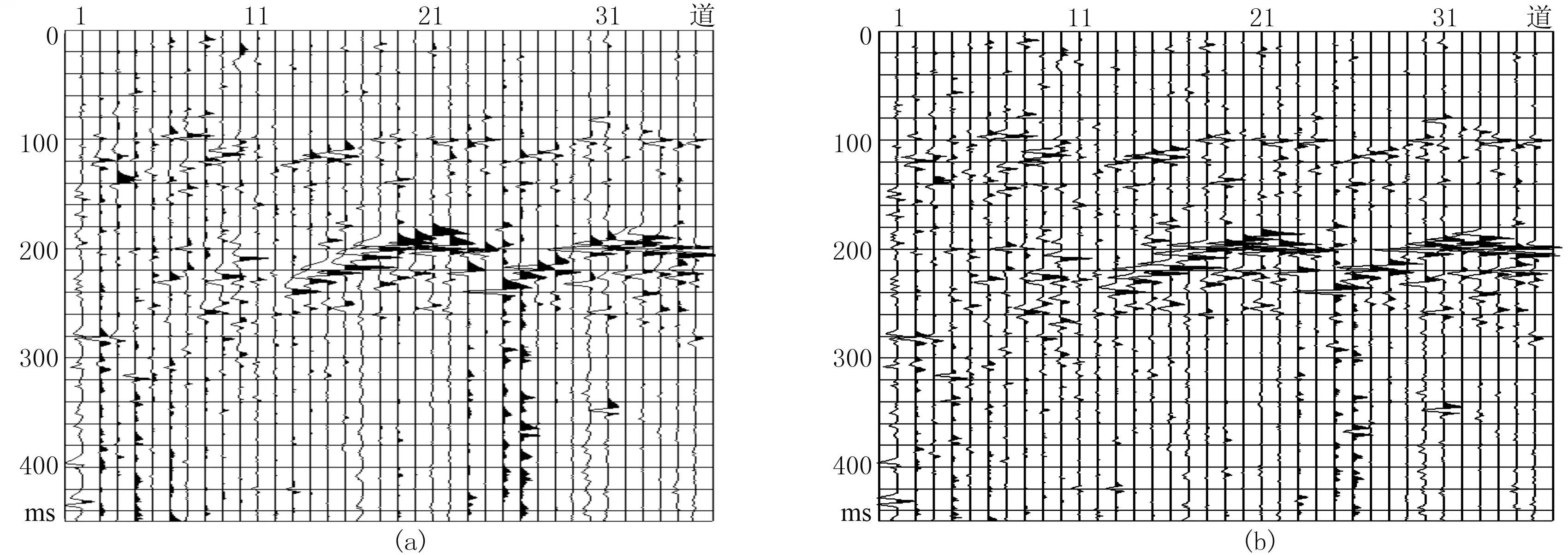
图4 不同稀疏率下压缩感知微地震信号重建结果

图5 不同稀疏率下基于独立分量分析和压缩感知微地震信号重建结果
5 实际资料处理结果分析
通过对混合矩阵的正交化以及稀疏率的选取,实现了独立分量压缩感知微地震弱信号提取重建的方法。为了验证方法的应用效果,对实际微地震资料进行了试算,结果如图6所示。由图可见,独立分量与压缩感相结合的处理方法除了增强微地震弱信号之外,还较好地提取出了淹没在噪声中的有效信号,说明了该方法的有效性。A地区微地震资料中、上部的干扰信号得到了很好的压制;B地区微地震资料处理结果不仅压制了区域的干扰噪声,还提取出了部分被淹没的有效信号,凸显了初至信号,大大提高了微地震资料的信噪比,有利于初至信号的拾取;C地区微地震资料的上部、下部的干扰噪声得到了压制,凸显了中部有效信号。不同地区的微地震资料的试算结果都说明,独立分量与压缩感相结合的处理方法能取得很好的处理效果,具有广泛的适用性。
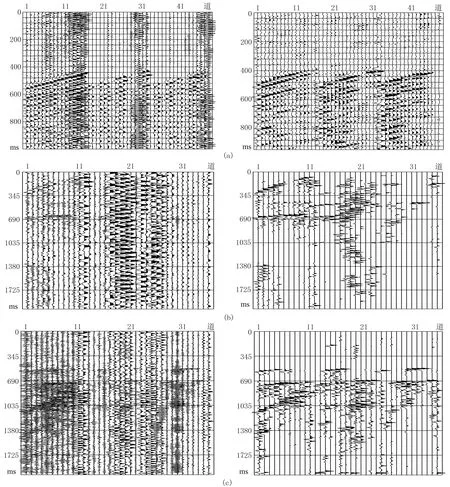
图6 不同地区实际微地震资料处理前(左)、后(右)对比
6 结论
微地震弱信号具有较强的模糊性和较差的稀疏性,直接通过压缩感知技术进行弱信号的提取难以取得理想的效果。独立分量分析(盲源分离分析)方法,虽然具有较强的信号分离能力,但是分离的有效信号具有一定的不确定性。本文结合两种方法的特点,提出了独立分量压缩感知弱地震信号提取方法,较好地实现了微地震弱反射信号的提取。
(1)在混合矩阵估计过程中,根据微地震记录数据特征,合理地组合观测矩阵,尽量使矩阵正交化,这种考虑数据结构组成的正交化矩阵减小了分离有效独立分量的不确定性。
(2)针对独立变量分析混合矩阵的维数确定关键问题,设计了自适应方法,能够较准确地确定混合矩阵的维数。
(3)基于稀疏度、稀疏率和微地震波传播特征综合考虑稀疏度的选取,增强了弱信号提取的可靠性。
[1] 孟小红,吴何珍,刘国峰.盲源反褶积方法与应用研究.石油地球物理勘探,2005,40(6):642-645. Meng Xiaohong,Wu Hezhen,Liu Guofeng.Study of blind deconvolution and application of method.OGP,2005,40(6):642-645.
[2] 宋维琪,杨勤勇,郭全仕等.地面微地震资料弱信号提取方法研究.石油物探,2013,52(2):131-135. Song Weiqi,Yang Qinyong,Guo Quanshi et al.Weak signal extraction method for surface microseismic monitoring data.GPP,2013,52(2):131-135.
[3] 戴琼海,付长军,季向阳.压缩感知研究.计算机学报,2011,34(3):425-434. Dai Qionghai,Fu Changjun,Ji Xiangyang.Research on compressed sensing.Chinese Journal of Computers,2011,34(3):425-434.
[4] Candès E,Wakin M.An introduction to compressive sampling.IEEE on Signal Processing Magazine,2008,25(2):21-30.
[5] Donoho D,Tsaig Y.Extensions of compressed sen-sing.Signal Processing,2006,86(3):533-548.
[6] 印兴耀,刘杰,杨培杰.一种基于负熵的Bussgang地震盲反褶积方法.石油地球物理勘探,2007,42(5):499-505. Yin Xingyao,Liu Jie,Yang Peijei.A negative entropy-based Bussgang seismic blind deconvolution.OGP,2007,42(5):499-505.
[7] 刘喜武,高伟,张宁等.基于带状混合矩阵ICA实现地震盲反褶积.地球物理学进展,2007,22(4):1153-1163. Liu Xiwu,Gao Wei,Zhang Ning et al.ICA with banded mixing matrix based seismic blind deconvolution.Progress in Geophysics,2007,22(4):1153-1163.
[8] 高伟.基于独立变量分析的盲反褶积研究[学位论文].山东青岛:中国海洋大学,2011. Gao Wei.Blind Deconvolution Based on Independent Component Analysis[D].Ocean University of China,Qingdao,Shandong,2011.
[9] 王维强.独立分量分析在地震勘探中的应用研究[学位论文].山东青岛:中国石油大学(华东),2012. Wang Weiqiang.Application of Independent Component Analysis in Seismic Exploration[D].China University of Petroleum (East China),Qingdao,Shandong,2012.
[10] Wadayama T.Sufficient condition for perfect recovery in compressed sensing.The Brain & Neural Networks,2010,17(2):63-69.
[11] Pennec E L,Mallat S.Sparse geometrical image representation with bandelets.IEEE Transactions on Image Processing,2005,14(4):423-438.
[12] 周灿梅.基于压缩感知的信号重建算法研究[学位论文].北京:北京交通大学,2010. Zhou Canmei.Research on Signal Reconstruction Algorithms Based on Compressed Sensing[D].Beijing Jiaotong University,Beijing,2010.
[13] Baraniuk R G,Cevher V,Duarte M F et al.Model based compressive sensing.IEEE Transactions on Information Theory,2010,56(4):1982-2001.
[14] Gholami A.Non-convex compressed sensing with frequency mask for seismic data reconstruction and denoising.Geophysical Prospecting,2015,62(6):1389-1405.
[15] 周亚同,王丽莉,蒲青山.压缩感知框架下基于K-奇异值分解字典学习的地震数据重建.石油地球物理勘探,2014,49(4):652-660. Zhou Yatong,Wang Lili,Pu Qingshan.Seismic data reconstruction based on K-SVD dictionary learning under compressive sensing framework.OGP,2014,49(4):652-660.
[16] 郭树旭,张驰,曹军胜等.基于压缩感知归一化关联成像实现目标重构.光学精密工程,2015,23(1):288-294. Guo Shuxu,Zhang Chi,Cao Junsheng et al.Object reconstruction by compressive sensing based normalized ghost imaging.Optics and Precision Engineering,2015,23(1):288-294.
[17] 方红,杨海蓉.贪婪算法与压缩感知理论.自动化学报,2011,37(12):1413-1421. Fang Hong,Yang Hairong.Greedy algorithms and compressed sensing.Acta Automatica Sinica,2011,37(12):1413-1421.
[18] Yin H,Li J,Chai Y et al.A survey on distributed compressed sensing:theory and applications.Frontiers of Computer Science,2014,8(6):893-904.
[19] 郭科,郭思,何国柱等.基于独立分量分析的多次波盲分离方法研究.地球物理学进展,2010,25(3):1075-1080. Guo Ke,Guo Si,He Guozhu et al.A method of multiple blind separation based on ICA.Progress in Geophysics,2010,25(3):1075-1080.
[20] 谢忠德.基于稀疏表示的盲信号分离算法研究[学位论文].广东广州:广东工业大学,2012. Xie Zhongde.Study on Blind Signal Separation Algorithm Based on Sparse Representation [D].Guang-dong University of Technology,Guangzhou,Guangdong,2012.
[21] Donoho D L.Compressed sensing.IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[22] Candes E J,Romberg J,Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information.IEEE Transactions on Information Theory,2006,52(2):489-509.
[23] 王新全,耿瑜,Ru-shan Wu等.基于压缩感知的Drea-mlet域数据重构方法及应用.石油地球物理勘探,2015,50(3):399-404. Wang Xinquan,Geng Yu,Ru-shan Wu et al.Seismic data reconstruction in Dreamlet domain based on compressive sensing.OGP,2015,(3):399-404.
[24] 白兰淑,刘伊克,卢回忆等.基于压缩感知的Curvelet域联合迭代地震数据重建.地球物理学报,2014,57(9):2937-2945. Bai Lanshu,Liu Yike Lu Huiyi et al.Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing.Chinese Journal of Geophysics,2014,57(9):2937-2945.
[25] 吕文彪,尹成,张白林等.利用独立分量分析法去除地震噪声.石油地球物理勘探,2007,42(2):132-136. Lv Wenbiao,Yin Cheng,Zhang Bailin et al.Using in-dependent component analysis to noise.OGP,2007,42(2):132-136.
[26] 李稳,刘伊克,刘保全等.基于稀疏分布特征的井下微地震信号识别与提取方法.地球物理学报,2016,59(10):3869-3882. Li Wen,Liu Yike,Liu Baoquan et al.Downhole microseismic signal recognition and extraction based on sparse distribution features.Chinese Journal of Geophysics,2016,59(10):3869-3882.
[27] Bruckstein A,Donoho D,Elad M.From sparse solutions of systems of equations to sparse modeling of signals and images.SIAM Review,2009,51(1):34-81.
(本文编辑:宜明理)

宋维琪 教授,博士生导师,1964年生; 1987年毕业于长春地质学院应用地球物理专业,获学士学位;1996年毕业于中国石油大学(华东)应用地球物理专业,获硕士学位;2002年毕业于中国石油大学(华东)应用地球物理专业,获博士学位;现在中国石油大学(华东)地球物理系从事地球物理方面的教学和科研,主要研究领域包括地震储层预测和压裂微地震监测等。
1000-7210(2017)05-0984-06
P631
A
10.13810/j.cnki.issn.1000-7210.2017.05.011
*山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email:swq1123@126.com
本文于2016年6月15日收到,最终修改稿于2017年8月9日收到。
本项研究受国家科技重大专项“水力压裂实时监测与地质工程一体化评估技术”(2016ZX05023-004)资助。
