基于同相轴追踪的三维地震资料多次波压制方法
2017-11-01李金山
谭 军 宋 鹏* 李金山 王 磊
(①中国海洋大学海洋地球科学学院,山东青岛 266100; ②青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛 266071; ③中国海洋大学海底科学与探测技术教育部重点实验室,山东青岛 266100)
基于同相轴追踪的三维地震资料多次波压制方法
谭 军①②③宋 鹏*①②③李金山①②③王 磊①
(①中国海洋大学海洋地球科学学院,山东青岛 266100; ②青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛 266071; ③中国海洋大学海底科学与探测技术教育部重点实验室,山东青岛 266100)
谭军,宋鹏,李金山,王磊.基于同相轴追踪的三维地震资料多次波压制方法.石油地球物理勘探,2017,52(5):894-905.
提出了一种基于同相轴追踪的三维多次波压制方法,在引入三维高分辨率叠加速度谱的基础上,进行多次波同相轴的高精度追踪,并将追踪到的多次波同相轴组成准多次波记录,然后利用f-k滤波方法实现在多次波同相轴所属短时窗内的多次波压制。模型实验和实际数据测试均表明,该方法的多次波剔除效果明显优于高精度抛物线Radon变换法,并且其计算效率也明显高于高精度抛物线Radon变换法,因此基于同相轴追踪的三维多次波压制方法更适合于针对“海量”数据的三维多次波压制处理。
多次波 同相轴追踪 叠加速度谱f-k滤波
1 引言
目前地震勘探仍主要利用一次反射波进行成像,地震记录中的直达波、浅层折射波和多次波等均被视为干扰波,其中多次波的识别与压制一直是海上地震勘探领域的研究热点之一。常规多次波剔除方法主要有预测反褶积技术、基于视速度差异的多次波压制方法以及基于波动理论的多次波压制方法等。预测反褶积[1,2]具有高效率的优点,但存在明显的局限性。多次波的周期呈时变、空变特征,因此无法给定准确的预测步长,从而导致多次波残余或损伤有效信号;而且该方法难以有效衰减长周期多次波(周期大于100ms的多次波)。在基于波动理论的多次波压制方法中,由于不需要任何先验信息就能有效地压制地震记录中的多次波,自由界面多次波衰减方法(SRME)[3-8]已成为二维地震数据处理的首选方法之一。Dedem等[9]、Pica[10]与Baumstein等[11]将该方法拓展为三维的自由界面多次波衰减方法[9-13],但是其难以有效压制远炮检距道中的多次波,而且运算量较大,限制了三维SRME的实际应用。
由于可兼顾衰减效果与处理效率,基于视速度差异的多次波压制方法在实际三维地震数据处理中得到了广泛应用。Ryu[14]提出了基于f-k视速度滤波的压制方法,首先在叠加速度谱中拾取介于多次波能量范围和一次波能量范围之间的叠加速度,然后基于该速度对输入的共中心点(CMP)道集进行动校正,多次波同相轴由于校正不足而呈向下弯曲的形态,再应用f-k视速度滤波消除相应斜率范围的多次波信号。在Thorson等[15]提出的Radon变换的基础上,Hampson[16]认为若以一次波的速度做动校正,多次波同相轴将近似为抛物线,从而可应用抛物线形式的Radon变换方法消除CMP道集中的多次波。为克服时间和空间上的截断效应[17],人们又提出了通过稀疏反演获得较高速度分辨率的高精度抛物线Radon变换法[18]与λ-f域高效抛物线Radon变换[19]。目前在实际地震资料处理中,抛物线Radon变换法已得到了广泛的应用[20-22],但仍然存在如下问题[23]:①经动校正后的多次波同相轴并非严格的抛物线,在Radon域难以真正“聚焦”,从而影响了压制效果;②近炮检距道的时差较小,难以消除强振幅多次波同相轴;③动校正、反动校正等存在拉伸效应,不仅影响了多次波的衰减效果,且会导致处理前、后记录的畸变。除此之外,海上三维地震数据的CMP道集中各道在空间上分布的不均匀性会降低Radon变换的精度[24]。
为提高三维地震资料多次波的衰减效果,本文提出了一种基于同相轴追踪的三维地震资料多次波压制方法(下文中简称为“同相轴追踪法”)。首先利用同相加权技术生成高分辨率的三维叠加速度谱,并根据一次波的叠加速度确定多次波的叠加速度范围,然后基于同相轴追踪技术确定时—空域中的多次波同相轴,再通过同相轴重排与道选排的方式建立准多次波记录,最后采用f-k扇形滤波法消除已被校正为水平的多次波同相轴。理论模型与野外资料的处理结果均验证了该方法明显优于高精度抛物线Radon变换法,而且显著提高了计算效率,更适合于海量数据的三维多次波压制。
2 基于同相轴追踪的三维地震资料多次波衰减
在水平层状介质条件下,三维地震数据CMP道集中的反射波同相轴符合双曲面规律,甚至在复杂地质环境中,诸如倾斜波阻抗界面、尖灭点等的反射同相轴也可近似看作双曲面,而叠加速度谱的本质即是应用不同叠加速度的双曲面对CMP道集进行扫描叠加。因此三维地震数据CMP道集中的一次波和多次波同相轴与其叠加速度之间存在明显的对应关系,理论上,可利用一次波或多次波的叠加速度对CMP道集中的一次波或多次波进行追踪。鉴于此,本文方法在生成高分辨率多次波叠加速度谱的基础上,实现多次波同相轴的追踪,进而基于道重排的准多次波记录应用f-k滤波实现多次波同相轴的剔除。
2.1 求取高分辨率多次波叠加速度谱
对输入的CMP道集d(n,t)作速度叠加变换[15],将得到横向坐标为叠加速度v、纵坐标为零炮检距时τ的速度域记录,基于三维地震记录的计算公式可表示为
(1)
式中:u为速度域记录;n、N分别为道号和总道数(1≤n≤N);xn、yn分别表示第n道记录在x、y方向的炮检距。
对记录u(v,τ)取绝对值,即可获得三维叠加速度谱E(v,τ)
E(v,τ)=|u(v,τ)|
(2)
Wang[17]详细分析了抛物线Radon变换的时间与空间截断效应,其结论同样适用于速度叠加变换(等价于双曲Radon变换),即叠加速度谱的能量形态并非集中于团状,其包括水平和倾斜两条长“尾”的“剪刀”形状,这既降低了速度谱的分辨率,又会严重影响后续同相轴追踪的精度。与二维情形相比,三维CMP道集的地震道空间分布更不均匀,从而进一步加重了速度叠加变换的截断效应。为压制叠加能量团的畸变,可对初步计算的叠加速度谱进行同相加权处理。在Stoffa等[25]提出的二阶同相加权因子的基础上,本文给出了高阶同相加权因子的计算公式

(3)
式中:λ(λ≥2)表示阶数,λ值越大则s(v,τ)的分辨率越高;L表示时窗长度;C为保证分母不为0的常数,一般可取平均振幅的0.01~0.001。
利用式(3)计算的因子s(v,τ)对三维速度谱进行同相加权,则式(2)可进一步表示为
E(v,τ)=|s(v,τ)u(v,τ)|
(4)
得到高精度的三维叠加速度谱之后,还需要据此确定多次波的叠加能量范围。一般来说,多次波在低速的海水层(或较浅层介质)中发生多次震荡,其叠加速度通常低于相同时刻的一次波叠加速度。通过叠加速度分析可获得一次波叠加速度v随零炮检距时τ变化的曲线,可表示为
v=f(τ)
(5)
为了保证切除全部的一次波能量,需要给定时变的速度偏移量Δv(τ),则最终的速度切除线描述为一次波速度值与速度偏移量之和,即
c(τ)=f(τ)-Δv(τ)
(6)
式中:c表示最终的速度切除值;Δv介于-50~200m/s之间。
通过直接切除一次波叠加速度范围的方式获得只包含多次波同相轴叠加能量的速度谱,将E(v,τ)中速度值大于c(τ)的范围均设置为0,而低于c(τ)的范围不变,即
(7)
建立长、宽以及最大深度分别为5000、5000与2000m且包含6套地层的水平层状介质模型(各层速度和厚度见表1),输入主频为40Hz的雷克子波作为震源,基于表2的三维观测系统参数通过射线追踪方法模拟的地震记录(工区中心位置的CMP道集)如图1a所示。可以看出,时间与空间截断效应导致速度谱中的叠加能量不聚焦,其中箭头所指为2~5阶的海底全程多次波(图1a、图1b)。利用式(3)对初始速度谱进行同相加权与适度平滑后得到适于等值线追踪的速度谱(图1c),其上覆实线为拾取的一次波速度曲线,而虚线为偏移量Δv=175m/s的曲线,切除谱中速度高于虚线的部分即可获得仅包含多次波叠加能量的速度谱(图1d)。
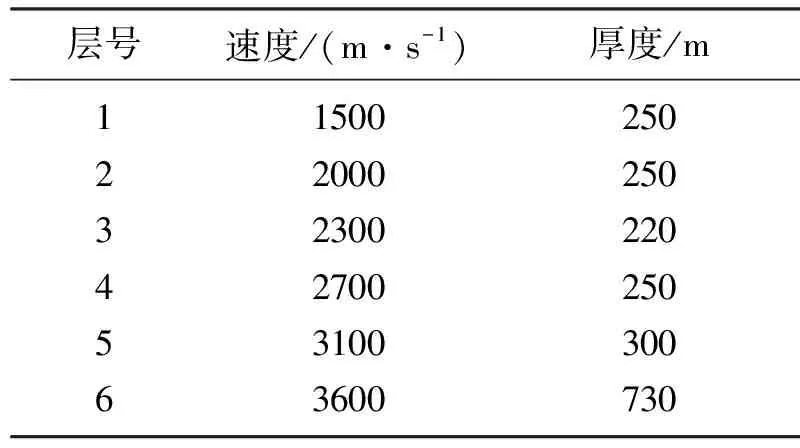
表1 三维水平层状模型参数

表2 三维海上地震观测系统参数
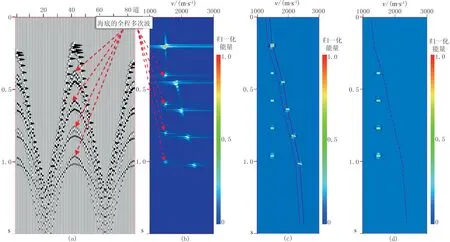
图1 射线追踪法模拟地震记录及其多次波速度谱
2.2 多次波同相轴的追踪
由于三维CMP道集中的双曲同相轴与叠加速度谱中的能量团一一对应,因此可利用等值线追踪方法确定谱内的能量团,进而获得三维CMP道集中相应双曲同相轴的旅行时信息。具体实现过程为:首先基于多次波叠加速度谱通过等值线追踪方法求出叠加能量团的分布范围,然后寻找各能量团中的极值能量位置,最后可根据该点坐标拟合出时—空域中的相应同相轴。
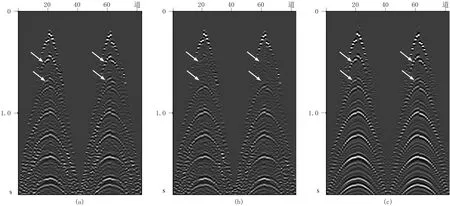
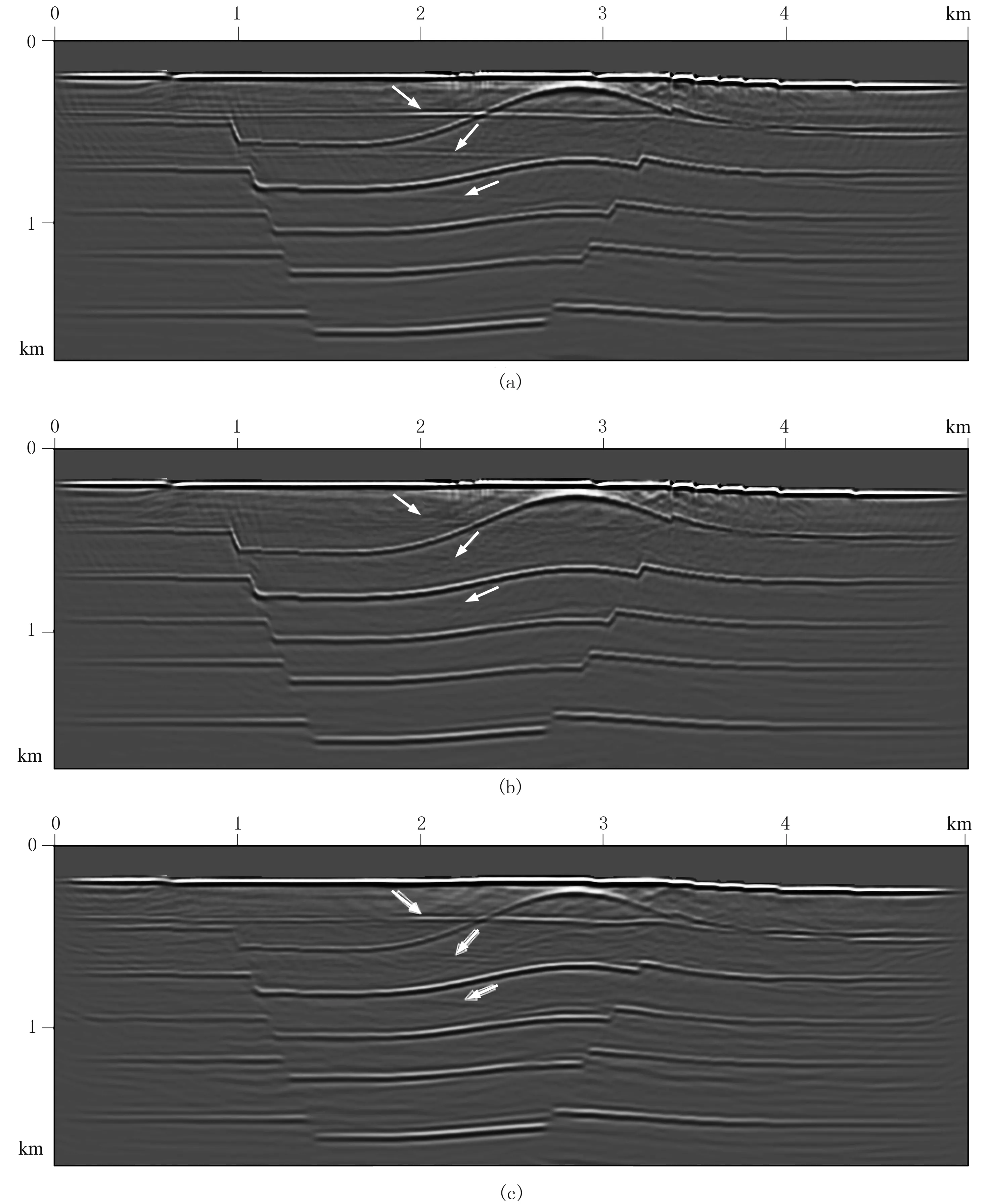
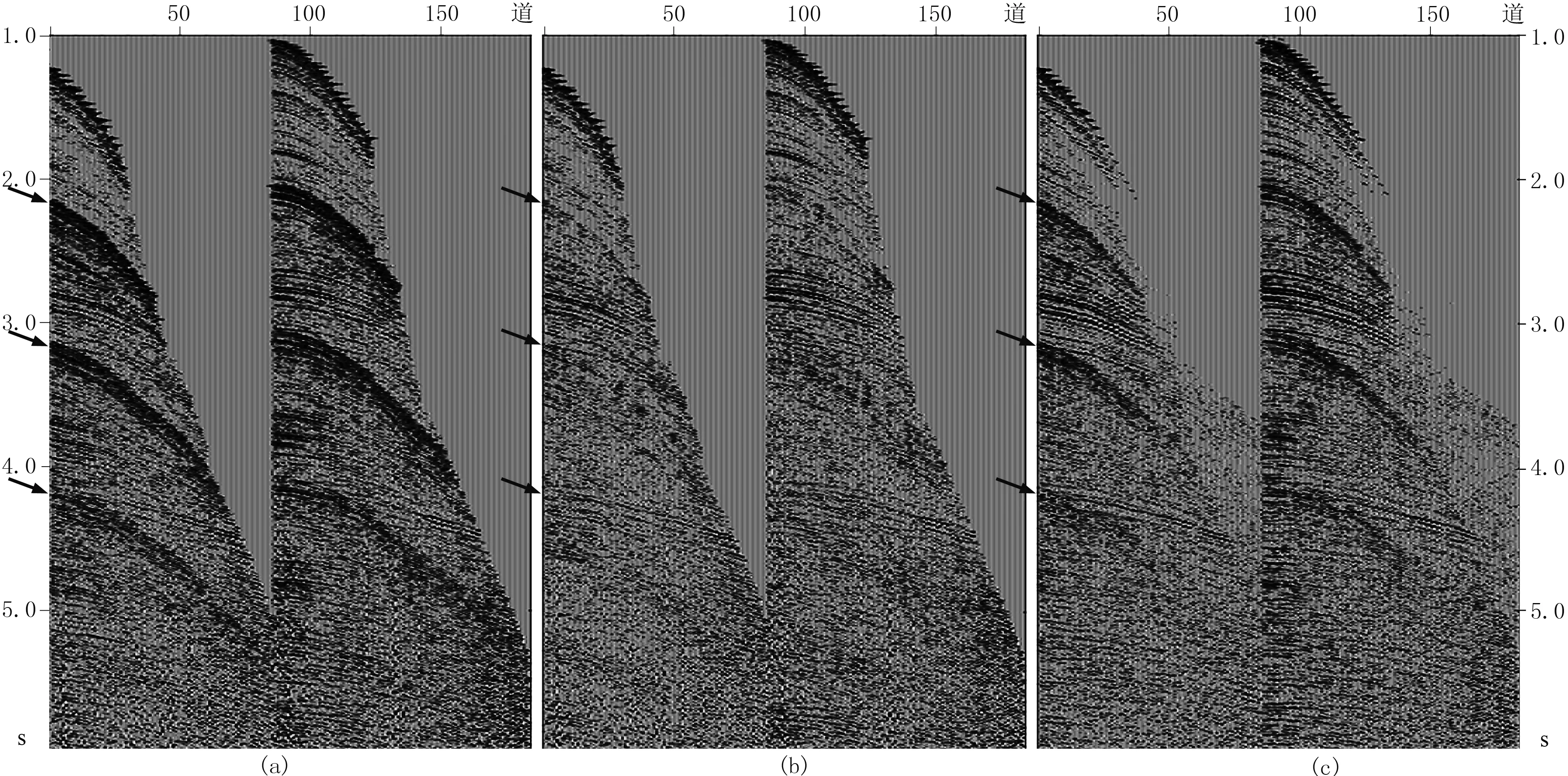
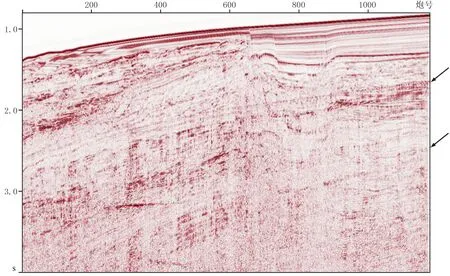
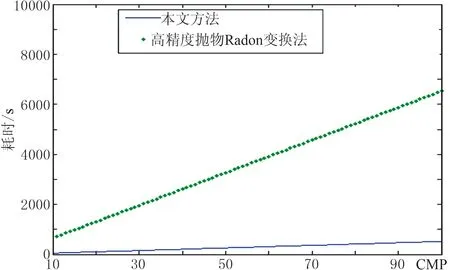
在利用等值线追踪的方法追踪速度谱中的各能量团时,由于叠加速度v和零炮检距时τ的离散采样导致速度叠加能量的离散,当追踪能量为E0(0 图2 相邻样点间的线性插值示意图 图2为相邻样点间的线性插值示意图。可以看出,在图2中,样点A、B、C、D对应的能量值分别为EA、EB、EC和ED,假定EA、EB和ED均大于追踪能量E0,而EC小于E0,则要追踪的点F、G位于BC与CD之间,可通过 (8) 确定。式中: |BF|、|FC|、|DG|、|GC|分别为B与F、F与C、D与G、G与C点间的距离。计算出点F和点G后,则可确定相应等值线在矩形网格ABCD中的走势,如图2中箭头GF所示。 (9) 式中1≤i≤I为同相轴序号,I≥1表示追踪的能量团个数。 2.3 基于准多次波记录道重排的多次波同相轴压制 (10) 为了提高滤波效率,将多次波同相轴记录ei(n,t)沿旅行时方向以一定间隔组合为准多次波记录 m[n,t′=t+i(l+Δl)]=ei(n,t) (11) 式中Δl指同相轴间距。为了有效剔除所有多次波同相轴,要求各多次波同相轴在原始记录d(n,t)中均不相交或重合(部分重合)。 图3为图1a数据同相轴追踪多次波衰减结果。可以看出,通过等值线追踪方法在多次波速度谱中圈定各同相轴的叠加能量团(图3a中的彩色等值线范围);然后追踪出原始记录中彩色曲线①~④标记的多次波同相轴(图3b),截取各同相轴合成准多次波记录(图3c,由于记录长度的限制导致椭圆范围内同相轴不连续);然后按照炮检距顺序对该记录进行道重排(图3d);再利用f-k扇形滤波消除该记录中处于水平状态的多次波同相轴(图3e); 最后将图3e所示记录中各同相轴截出并变换到原始CMP道集,得到最终结果(图3f),其中的多次波同相轴均被有效消除。 图3 图1a数据基于同相轴追踪的多次波衰减结果 由于原始记录d(n,t)中的多次波同相轴可能相交或重合(部分重合),且多次波同相轴的速度叠加能量通常具有一定差异,仅通过一次追踪压制无法消除原始记录d(n,t)中的所有多次波同相轴,现采用迭代的多次波同相轴追踪与衰减方法,基本步骤如下。 (1)为了保证同相轴追踪过程的稳定性,需要确定多次波同相轴密度Nm与追踪能量阈值E0参量。其中Nm为单位长度时窗内多次波同相轴数目的平均值,E0用以界定所追踪同相轴的叠加能量范围。 可通过对地震记录与叠加速度谱的观察分析给定Nm与E0的值。 (12) (3)重复步骤(2),直至剩余速度谱中的极值Emax小于阈值E0为止(图4)。 图4 迭代的多次波同相轴追踪衰减流程 为了检验三维多次波压制效果,建立长、宽以及最大深度分别为5000、5000与2000m的简单速度模型(图5),其各反射界面起伏形态如图5a所示。为了更直观地显示模型结构与速度特征,取其沿纵测线方向、联络测线方向的纵波速度模型切片(图5b与图5c)。该速度模型包含7套匀速地层,沿纵测线方向,速度模型左部发育一穹窿构造,右侧为凹陷构造,在穹窿两侧存在走向均垂直于纵测线方向的两个断层; 速度模型顶部为海水层,其深度介于150~250m之间。 图5 三维理论速度模型及其反射界面形态 在图5所示的纵波速度模型基础上,建立含有海水层的横波速度模型(水层横波速度为0),水层以下介质横波与纵波的关系式为 (13) 式中:vS、vP分别为横、纵波速度。根据加德纳公式建立密度模型[26],设水层密度为1.0g/cm3,而岩层密度与纵波速度的关系式为 (14) 基于上述模型采用野外常用的奇偶炮激发方式进行正演模拟(观测系统参数见表2),震源采用主频为25Hz的雷克子波,设海面为自由界面,基于弹性波波动方程有限差分法模拟一套含有强多次波干扰的地震记录。令奇、偶号航线的方向分别为正向与负向,共模拟了44条航线的炮集记录,每条航线激发了119炮,44条航线共5236炮。经过横、纵波分离后,取仅包含纵波分量的记录作为原始地震记录。图6是位于穹窿构造上方的炮集记录,其中含有大量振幅较强、速度与一次波较为接近的多次波,如箭头指向的2~3阶海底全程多次波,它们妨碍了对有效波的识别分析,进而会严重影响地震剖面的成像质量。 图6 穹窿构造上方的原始单炮记录 基于一次波叠加速度,分别应用同相轴追踪法和高精度抛物线Radon变换法进行多次波的压制。为避免动校拉伸效应对高精度抛物线Radon变换法的影响,对原始记录进行了远炮检距道信号的切除。图7为不同方法衰减多次波前、后的CMP道集对比。相应面元中心接近模型的中心位置(x=2475m,y=2700m),其包含相邻后两条航线的地震道,覆盖次数达到84次。可以看出,原始记录中箭头所指为2~4阶海底全程多次波,其振幅明显强于同时段的一次反射波。图8为从原始记录中去除的多次波。对比图7b与图7c以及图8a与图8b可知,同相轴追踪法较好地消除了原始记录中的多次波(图7b),去除的多次波记录中并不存在一次波信息(图8a);而高精度抛物线Radon变换法由于动校正后的多次波同相轴并不符合抛物线规律,未能有效压制多次波,而且导致明显的波形畸变(图7c),减掉的多次波记录中存在明显的一次波(图8b)。 图7 不同方法多次波压制结果对比 图8 从图7a中去除的多次波 图9为基于图5理论模型不同方法衰减多次波后逆时偏移剖面对比。可以看出,同相轴追踪法较好地消除了箭头所指的海底全程多次波,剖面中的穹窿构造反射同相轴的连续性明显增强(图9b箭头处);而在高精度抛物线Radon变换法消除多次波的偏移剖面中仍然存在明显的多次波残余(图9c箭头处)。 图9 基于图5不同方法衰减多次波后逆时偏移剖面对比 基于南海A区三维地震资料进行多次波压制,该工区所在海域为硬海底地区,沿主测线方向海水由浅至深变化(水深介于400~1000m)。地震资料的野外采集参数为:采用常用的奇偶炮激发方式,原始数据共有96条航线,总炮数达142159炮,其他参数见表3。相应的原始炮集记录中存在多阶的强海底全程多次波以及与海底有关的微屈多次波。抽取单一航线中各炮记录的最小炮检距道,然后根据炮号递增的顺序组成最小炮检距剖面(图10)。可以看出,利用多次波的周期性可识别出箭头所指的2~3阶海底全程多次波,由于振幅较强,这些多次波掩盖了同时段较弱的一次波。 图11为南海A区地震数据不同方法衰减多次波结果对比。可以看出,图11b中的海底及下伏波阻抗界面的强鸣震多次波已被完全消除(图11b箭头处),而高精度抛物线Radon变换法衰减多次波的CMP道集中存在较强的多次波残余(图11c中箭头处),且动校正与Radon变换导致该记录存在明显的波形畸变。图12为图11a数据不同方法去除的多次波。可以看出,去除的多次波中同相轴追踪法去除的多次波能量明显比高精度抛物线Radon变换法强(图12a箭头处),而图12b中尚存在明显的一次波(图12b箭头处),这充分说明同相轴追踪法的多次波剔除效果明显优于高精度抛物线Radon变换法。 表3 三维海上地震观测系统参数 图10 南海A区三维原始地震记录B航线的最小炮检距剖面 图11 南海A区地震数据不同方法衰减多次波结果对比 图12 图11a不同方法去除的多次波 图13为图10数据同相轴追踪法衰减多次波的最小炮检距剖面。可以看出,海底及下伏波阻抗界面的强鸣震多次波已被完全消除(图中箭头处)。利用一次波的偏移速度场,对原始炮集记录与同相轴追踪法压制多次波后的炮集记录进行三维Kir-chhoff积分法叠前时间偏移,所得主测线方向的偏移剖面如图14所示。由于多次波速度与一次波的速度存在较大差异,偏移成像过程对多次波信号起到一定的压制作用,因此原始剖面中多次波振幅明显比原始最小炮检距剖面中的多次波信号弱,该剖面中仍然存在连续的多次波同相轴(如图14a箭头处)。图14b为同相轴追踪法压制多次波后的叠前时间偏移剖面,其中箭头指向的多次波同相轴得到较好压制,剖面中部一次波同相轴连续性明显增强,地质构造形态更加清晰。 在同等运行环境下,分别应用同相轴追踪法与高精度抛物线Radon变换法针对一定数量的CMP道集进行多次波压制,在此过程中统计上述方法所消耗的机时。图15为同相轴追踪法与高精度抛物线Radon变换法消耗机时与CMP道集数量的关系。 图13 图10数据同相轴追踪法衰减多次波的最小炮检距剖面 图14 多次波衰减前(a)、后(b)叠前时间偏移剖面对比 图15 消耗机时与CMP道集数量的关系 经过统计分析,同相轴追踪法与高精度抛物线Radon变换法完成100个CMP道集的处理所需时间分别为519s与6529s, 前者所耗机时仅为后者的7.95%,验证了同相轴追踪法在三维地震资料多次波压制中具有计算效率优势。 本文提出了基于同相轴追踪的三维地震资料多次波压制方法,首先通过切除一次波叠加能量的方式生成多次波叠加速度谱,然后利用同相轴追踪确定时—空域中的多次波同相轴,并将追踪的多次波同相轴组成准多次波记录进行f-k滤波。与高精度抛物线Radon变换法相比,同相轴追踪法无需对输入的CMP道集进行整体动校正,且能明显改善近炮检距道的多次波衰减效果;同时,仅在多次波同相轴所在的短时窗内滤波,降低了损伤一次波信号的几率。此外,同相轴追踪法的计算效率远高于高精度抛物线Radon变换法,因此更加适合海量三维地震数据的多次波压制。 [1] Peacock K L and Treitel S.Predictive deconvolution:theory and practice.Geophysics,1969,34(2):155-169. [2] Treitel S,Gutowski P R and Wagner D E.Plane-wave decomposition of seismograms.Geophysics,1982,47(10):1375-1401. [3] Verschuur D J,Berkhout A J,Wapenaar C P A.Adaptive surface-related multiple elimination.Geophysics,1992,57(9):1166-1177. [4] Verschuur D J,Berkhout A J.Estimation of multiple scattering by iterative inversion,Part Ⅱ: Practical aspects and examples.Geophysics,1997,62(5):1596-1611. [5] Berkhout A J,Verschuur D J.Estimation of multiple scattering by iterative inversion,Part Ⅰ: Theoretical considerations.Geophysics,1997,62(5):1586-1595. [6] 石颖,刘洪.基于GPU的表面多次波预测技术.石油地球物理勘探,2010,45(4):540-544. Shi Ying,Liu Hong.GPU-based surface multiple prediction technique.OGP,2010,45(4):540-544. [7] 井洪亮,石颖,李莹等.基于L1/L2范数的表面多次波自适应相减方法.石油地球物理勘探,2015,50(4):619-625. Jing Hongliang,Shi Ying,Li Ying et al.Surface-related multiple adaptive subtraction method based on L1/L2norm.OGP,2015,50(4):619-625. [8] 徐强,王征,史增园等.浅水多次波衰减.石油地球物理勘探,2015,50(2):238-242. Xu Qiang,Wang Zheng,Shi Zengyuan et al.Shallow water multiple attenuation.OGP,2015,50(2):238-242. [9] Dedem E J and Verschuur D J.3D surface-related multiple prediction: A sparse inversion approach.Geo-physics,2005,70(3):V31-V43. [10] Pica A.3D surface-related multiple modeling.The Leading Edge,2012,24(3):292-296. [11] Baumstein A,Hadidi M T.3D surface-related multiple elimination: Data reconstruction and application to field data.Geophysics,2006,71(3):E25-E33. [12] 王维红,井洪亮.基于稀疏反演三维表面多次波压制方法.地球物理学报,2015,58(7):2496-2507. Wang Weihong,Jing Hongliang.3D surface-related multiple elimination based on sparse inversion.Chi-nese Journal of Geophysics,2015,58(7):2496-2507. [13] 方云峰,聂红梅,张丽梅等.基于数据规则化和稀疏反演的三维表面多次波压制方法.地球物理学报,2016,59(2):673-681. Fang Yunfeng,Nie Hongmei,Zhang Limei et al.3D SRME based on joint regularization and sparse inversion.Chinese Journal of Geophysics,2016,59(2):673-681. [14] Ryu J V.Decomposition(DECOM) approach applied to wave field analysis with seismic reflection records.Geophysics,1982,47(6):869-883. [15] Thorson J R and Claerbout J F.Velocity-stack and slant-stack stochastic inversion.Geophysics,1985,50(12):2727-2741. [16] Hampson D.Inverse velocity stacking for multiple elimination.Journal of the Canadian Society of Exploration Geophysicists,1986,22(1):44-55. [17] Wang Y H.Multiple attenuation: coping with the spatial truncation effect in the Radon transform domain.Geophysical Prospecting,2003,51(1):75-87. [18] Sacchi M D and Ulrych T J.High resolution velocity gathers and offset space reconstruction.Geophysics,1995,60(4):1169-1177. [19] Abbad B,Ursin B,Porsani M J.A fast, modified parabolic Radon transform.Geophysics,2011,76(1):V11-V24. [20] 郭全仕,张卫华,黄华昌等.高精度拉冬变换方法及应用.石油地球物理勘探,2005,40(6):622-627. Guo Quanshi,Zhang Weihua,Huang Huachang et al.High-precision Random transform method and its application.OGP,2005,40(6):622-627. [21] 范景文,李振春,宋翔宇等.各向异性高分辨率Radon变换压制多次波.石油地球物理勘探,2016,51(4):665-669. Fan Jingwen,Li Zhenchun,Song Xiangyu et al.Multiple attenuation with anisotropic high-resolution Radon transform.OGP,2016,51(4):665-669. [22] 王保丽,Sacchi M D,印兴耀等.基于保幅拉东变换的多次波衰减.地球物理学报,2014,57(6):1924-1933. Wang Baoli,Sacchi M D,Yin Xingyao et al.Multiple attenuation based on amplitude preserving Radon transform.Chinese Journal of Geophysics,2014,57(6):1924-1933. [23] 谭军.自由界面多次波的预测与衰减[学位论文].山东青岛:中国海洋大学,2011. Tan Jun.The Prediction and Attenuation of Surface-related Multiple[D].Ocean University of China,Qing-dao,Shandong,2011. [24] Yilmaz Ö.Seismic Data Analysis: Processing,Inver-sion,and Interpretation of Seismic Data.SEG,2001,775-781. [25] Stoffa P L,Buhl P,Diebold J B et al.Direct mapping of seismic data to the domain of intercept time and ray parameter—A plane-wave decomposition.Geophysics,1981,46(3):255-267. [26] Gardner G H F,Gardner L W and Gregory A R.Formation velocity and density—the diagnostic basics for stratigraphic traps.Geophysics,1974,39(6):770-780. (本文编辑:金文昱) 1000-7210(2017)05-0894-12 P631 A 10.13810/j.cnki.issn.1000-7210.2017.05.002 谭军 讲师,1982年生;2005年毕业于中国海洋大学勘查技术与工程专业,获工学学士学位;2008年毕业于中国海洋大学地球探测与信息技术专业,获硕士学位;2011年获中国海洋大学海洋地球物理学博士学位,研究方向是海上地震勘探多次波预测与衰减;随后就职于中国海洋大学海洋地球科学学院,主要从事多次波预测压制研究、地震成像研究以及基于GPU集群平台的三维地震数据处理系统研发。 *山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院,266100。Email:pengs@ouc.edu.cn 本文于2016年11月28日收到,最终修改稿于2017年6月12日收到。 本项研究受国家自然科学基金(41574105、41674118)、国家重大科技专项(2016ZX05027-002)和青岛海洋科学与技术国家实验室鳌山科技创新计划项目(2016ASKJ13)联合资助。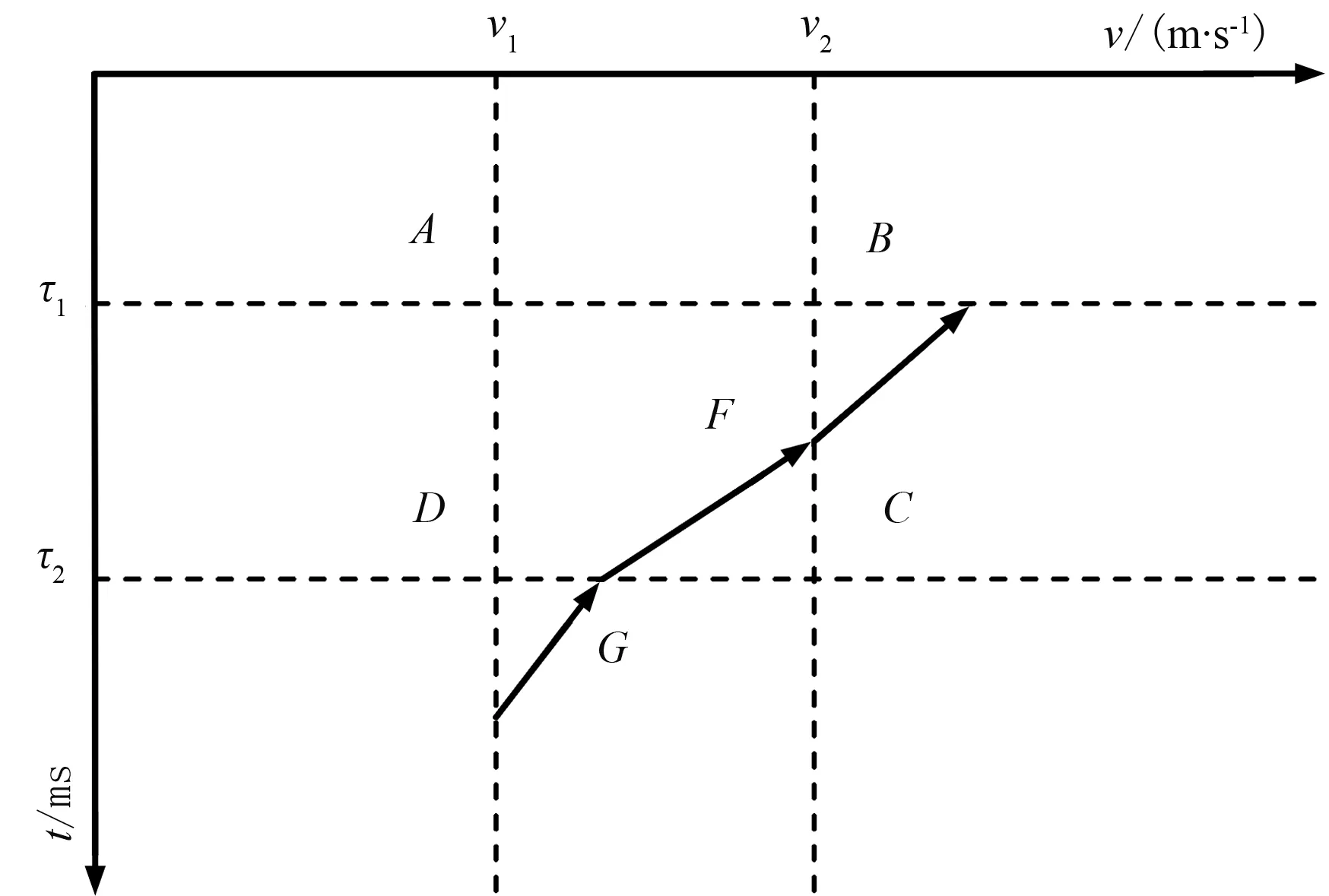
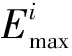


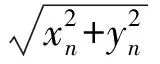
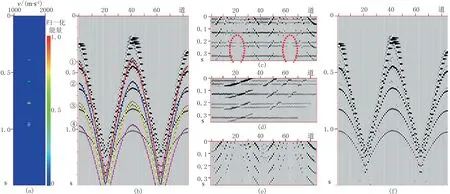
3 基于多次波同相轴追踪的三维地震资料多次波迭代衰减


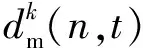

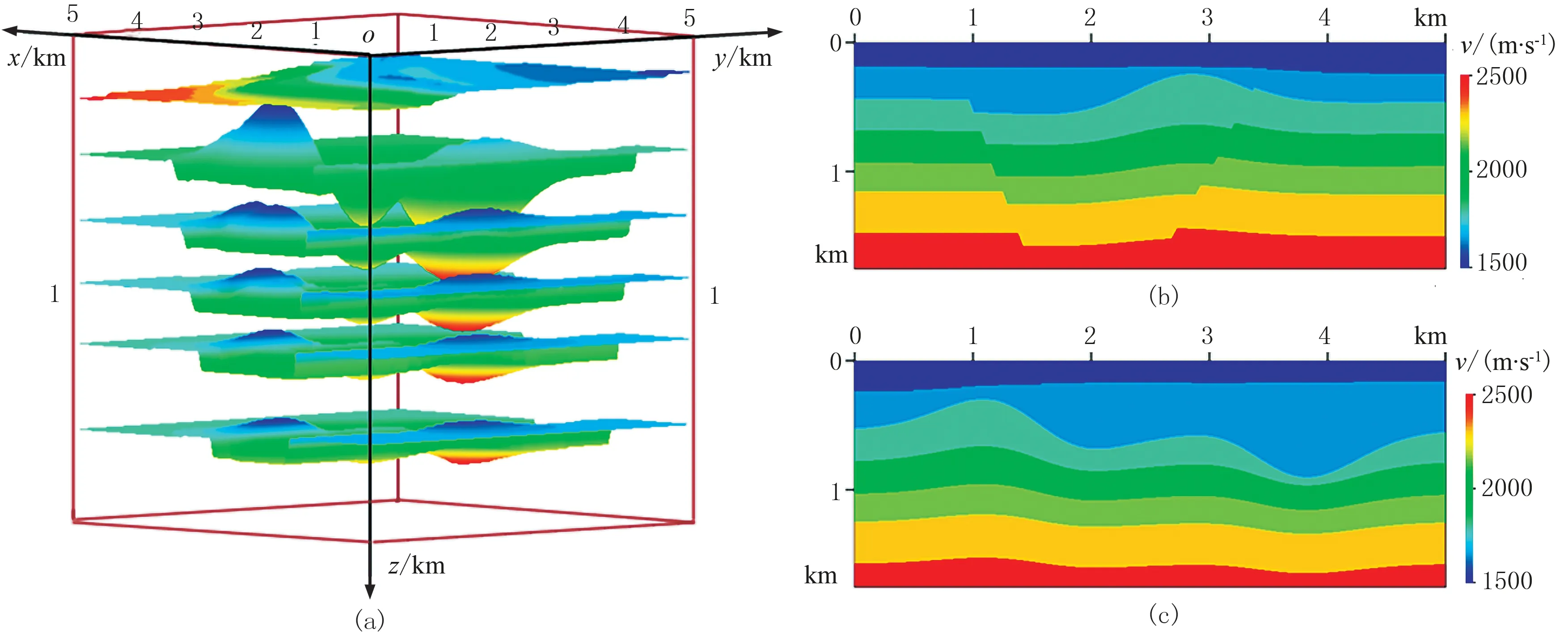
4 简单模型多次波衰减
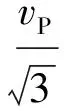
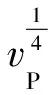


5 实际资料多次波压制



6 结束语

