基于LBM的多孔骨架热物性对固液相变的影响研究

宋林泉，陈宝明，2，3，*，郜凯凯

（1.山东建筑大学热能工程学院，山东济南250101；2.可再生能源建筑利用技术教育部重点实验室，山东济南250101；3.山东省建筑节能技术重点实验室，山东济南250101）

基于LBM的多孔骨架热物性对固液相变的影响研究

宋林泉1，陈宝明1，2，3，*，郜凯凯1

（1.山东建筑大学热能工程学院，山东济南250101；2.可再生能源建筑利用技术教育部重点实验室，山东济南250101；3.山东省建筑节能技术重点实验室，山东济南250101）

对不同物性骨架对固液相变过程的影响研究可为中低温相变储能技术的应用和发展奠定理论基础。文章基于格子玻尔兹曼方法（LBM），采用两区域焓—多孔介质模型研究了方腔内无填充多孔介质骨架固液相变过程，从孔隙尺度分析了相变过程的流动和传热机理，探讨了方腔内填充不同导热系数的骨架对于相变过程的影响。结果表明：在无填充多孔介质骨架方腔内固液相变过程中传热方式由热传导逐渐向自然对流换热转变，形成向右倾斜的糊状区；它的存在导致相变材料不能完全融化，且在方腔的左侧壁面处存在上窄下宽的固相相变材料；在填充多孔介质骨架方腔内，融化的初始阶段，高导热系数多孔骨架的相变材料融化速率较大，对相变换热起到了明显的促进作用，而当相变过程发展至准稳态阶段，受到右壁面处的低温影响和糊状区的综合作用，相变过程受到明显的抑制，且骨架的导热系数越大，其融化率越低。

固液相变；格子玻尔兹曼方法；糊状区；多孔骨架；两区域焓—多孔介质模型

Abstract：Changes of heat transfer and flow filled with different thermal conductivity skeleton on the solid-liquid phase change process set the theoretical foundation for the application and development of low temperature phase change energy storage technology.This paper has adopted the two-zone enthalpy-porous model to study the solid-liquid phase transition process based on the Lattice Boltamann Method（LBM）.On this basis，the solid-liquid phase change process in porousmedia was studied based on the pore scale tomainly analyze the influences of porous thermal conductivity on the phase change process.The results show that the heat conduction gradually shifts to the natural convection heat transfer which results in an above narrow and under thick mushy region.Because of the existence of themushy zone，the phase changematerial does not completelymelt causing a narrow top and wider bottom of the solid material at the left wall of the square cavity.For the solid liquid phase transition process of porousmedia，the high thermal conductivity porous skeleton has a higher melting rate.However，when the phase transition develops to the quasi steady state，the porous skeleton with high thermal conductivity has a significant effect on the natural convection heat transfer which indicates that the melting rate is less than that of the porous skeleton with low thermal conductivity.

Key words：solid-liquid phase transition； Lattice Boltamann Method； mushy region； porous skeleton；two-zone enthalpy-porousmodel

0 引言

多孔介质内固液相变传热流动研究广泛存在于各行各业中，例如建筑外围护结构内添加相变材料［1-4］可以有效地减弱室外不利环境对室内温湿度的影响。在相变过程中，相变材料特性（融化温度、相变半径）影响方腔内的流动、传热以及相变界面的移动。对于单质（如铝、铁等金属物质），其固液相变过程中有显著的固液交界面；而相变物质（如石蜡、羧酸、多元醇等有机物），其融化温度往往发生在一个区间，此时就会存在一个固相和液相共存的区域（糊状区）。由于两相界面随融化过程的进行而移动，在界面处的能量守恒条件是非线性的，同时伴随着热质交换的进行，因此相变过程是一个非稳态、非线性的问题。

Kazmierczak首次基于Darcy模型进行了多孔介质中相变材料融化的自然对流现象的研究［5］。Jany等从孔隙尺度分析了填充多孔介质方腔内相变材料的融化过程［6］，并总结出了自然对流换热强度对壁面平均Nu数的影响。之后，Bejan采用相同的方法研究了Ste数的影响［7］。近年来，利用金属泡沫和骨架的高导热性对蓄能换热器的相变传热效率强化进行逐渐重视。Mancin对具有不同相变温度的三种石蜡在同孔隙率、孔密度的铜泡沫中的固液相变过程进行了对比实验［8］。何叶从等基于焓法分析了相变墙板传热性能的影响因素［9］。崔娜等采用焓法分析了石膏基—石蜡相变储能构件在被动式建筑中的应用效果［10］。

固液相变过程中存在着界面能量守恒的非线性特征、变化过程的非稳定性以及孔介质结构的复杂性，现阶段多孔介质内固液相变过程的研究主要采用的是数值模拟方法。而格子玻尔兹曼方法LBM（Lattice Boltamann Method）与传统 CFD（Compntational Fluid Dynamics）方法相比，具有处理复杂边界、容易编程、后处理简单和并行性高等优点。并且在填充多孔介质方腔内的传热流动以及多相流的数值模拟等方面取得了许多成功的应用。许多学者将LBM应用在固液相变传热过程研究中。Wen等在前人对纯导热LBM模型研究的基础上，建立了固液相变过程中的的纯导热LBM模型［11］。夏莉等采用VOF（Volume of Fluid）模型研究了圆柱形容器中具有自由液面的石蜡相变过程，分析了多孔介质模型中形态系数对石蜡熔化过程的影响［12］。Gao等考虑局部非热平衡效应，使用 REV（Representative Elementary Volume）和孔隙尺度上的LBM模型对泡沫金属中的固液相变过程进行了模拟研究［13］。

虽然目前大量对无填充多孔介质的固液相变过程研究表明，相变过程中固液共存的区域（糊状区）会显著影响固液相变的过程［14-15］，但对于填充多孔骨架方腔的储能材料固液相界面的传递机理缺乏进一步的研究，尤其是相界面糊状区的传热和流动的模型缺少深入的探讨。文章拟以前期的研究为基础，根据非平衡热力学和复杂介质中的相变机理，建立糊状区的两区域模型，揭示无填充多孔介质内固液相变过程的流动和热质交换的规律，以及填充不同导热系数的骨架对固液相变过程的传热和流动的变化规律，为实际工程应用提供必要的理论依据，为中低温相变储能技术的研究和应用奠定理论基础。

1 多孔骨架的固液相变两区域模型构建

多孔骨架模型如图1所示，方腔的边长为H，腔体内填充摆放边长为1／15H的正方形多孔介质骨架共5×5个，计算可得其相应孔隙率为0.8889。其中黑色部分代表固体骨架，而白色部分为填充均匀的相变材料。方腔内部填充相变材料，其相变温度区间中心温度θm为0.25，其相应的相变温度半径θR为0.10。相变材料在融化过程中当温度达到θms＝θm-θR时开始融化；而完成融化时，对应的温度达到θml＝θm+θR，方腔上下壁面为绝热壁面，整个方腔内，初始温度θc＝0。融化的初始时刻，左侧的高温壁面温度θh为1，高于相变材料的融化温度。

基于糊状区的焓—多孔介质模型，文章提出两区域模型，即对糊状区中高液相率区（rfl＞rtr）采用液—固两相流，将其看作不同组分均匀混合的单相介质，将原来适用单质流体的宏观输运方程直接用于液—固两相流相流区域，而涉及到的相关物性参数则使用表征参数；而低含液率区域（rfl＞rtr）采用适用范围更广的Brinkmann-Forchheimer-Darcy多孔介质渗流模型，其中渗透率、形态系数由液相率计算得到，从而建立更加准确的数学模型。相变材料的融化过程可分为3个区域，分别为液相区（红色）、固相区（蓝色）以及固液共存区域——糊状区（介于红色和蓝色之间的区域），如图2所示。

图1 多空骨架模型图

图2 相变融化过程分区示意图

2 固液相变数学模型建立

2.1 控制方程建立

两区域模型中高低含液率的分界点rtr＝0.7。为了便于建立数学模型，作出了5项假设：（1）相变过程中液相区流体（含液率rfl＝1）视为不可压缩牛顿流体；（2）方腔内液相相变材料的流动为层流；（3）相变材料与填充腔体内的多孔介质骨架物性参数均视为常数；（4）考虑液相区内的自然对流，流体中的粘性耗散忽略不计，除密度外其它物性为常数；（5）相变过程中相变材料的体积变化忽略不计。

在假设的基础上，Brinkmann-Forchheimer-Darcy模型可表示为广义N—S方程的形式，在一定条件下广义N—S方程可以简化为标准的N—S方程，而基于孔隙尺度的流体流动仍遵循标准N—S方程，因此REV尺度的糊状区模型与孔隙尺度的固液相变过程可统一为一区域方程。基于焓—多孔介质模型，糊状区内多孔介质区域的孔隙率ε由该区域的液相率rfl获得，因此，孔隙尺度下含糊状区的固液相变的控制方程分别由式（1）～（3）分别表示为

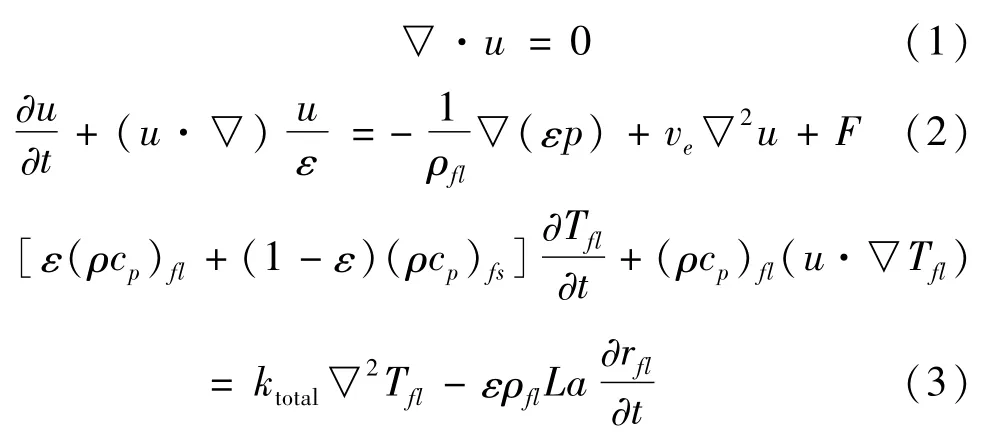
式中：fl为相变材料液相；fs为相变材料固相；s为多孔骨架；v为有效运动粘性系数，m2／s；u为渗流速度矢量，m／s；p为表观压力，Pa；ε为多孔介质孔隙率，ε＝0为固相区，ε＝1为液相区，0＜ε＜1为糊状区；k为导热系数，W／（m·K）；ktotal为有效导热系数，W／（m·K）；vfl表示液相流体的动力粘性系数，m2／s；β表示液相流体的热膨胀系数，1／K；F为外力源项由式（4）表示为

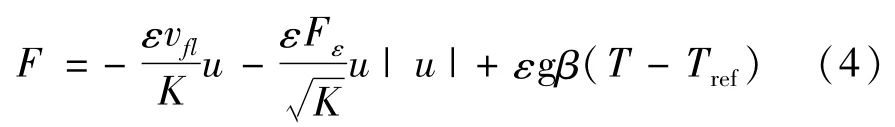
式中：K为多孔介质的渗透率；Fε为形状因子。

在糊状区的低含液率区域（rfl＜rtr），对应的渗透率K、有效导热系数 ktotal分别由式（5）、（6）表示为

在液相区rfl＝1（即ε＝1），控制方程演化为无多孔介质自然对流条件下固液相变的流动和传热控制方程；在固相区rfl＝0（即ε＝0），进而速度u＝0，控制方程则演化为导热的控制方程；在糊状区的低液相率区域0＜rfl＜rtr，即为多孔介质区域，该区域内流动、传热满足上述控制方程。

在高液相率1＞rfl＞rtr，液固两相流的表征导热系数、表征运动粘度由式（7）、（8）［16-17］表示为

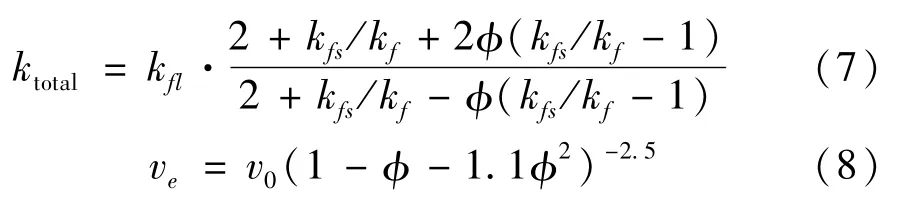
式中：φ为相变材料固相体积分数，即φ＝1-rfl。

多孔介质骨架传热为纯导热过程能量方程由式（9）表示为

式中：ks表示多孔骨架的导热系数；Ts表示多孔骨架的温度。

采用焓法［18］求解液相率，相变材料在某温度时的焓值由式（10）表示为

相变材料的焓值En和温度Tf之间的关系由式（11）表示为

式中：Ens、Enl分别为相变开始时相应温度Tfs的焓值和相变完成时对应温度Tfl相应的焓值；TR为相变半径，TR＝（Tfl-Tfs）／2。根据相变材料的液相率和焓值之间的关系，计算得到式（12）为

由式（10）、（11），结合式（12）可知，多孔介质骨架传热的纯导热方程（9）中的温度场与含液率是相互耦合的，可以通过数值迭代求解。为减少控制方程中的变量，探讨相变过程中糊状区对相变过程影响的机理，引入了无量纲参数

获得对应的无量纲控制方程：孔隙尺度下的连续性方程、动量方程、能量方程和多孔骨架能量方程分别由式（13）～（16）表示为

2.2 基于LBM的固液相变方程建立

采用双分布格子玻尔兹曼方法D2Q9模型进行求解，其模型对应的速度和温度演化方程及平衡态方程，由式（17）～（19）［19］分别表示为

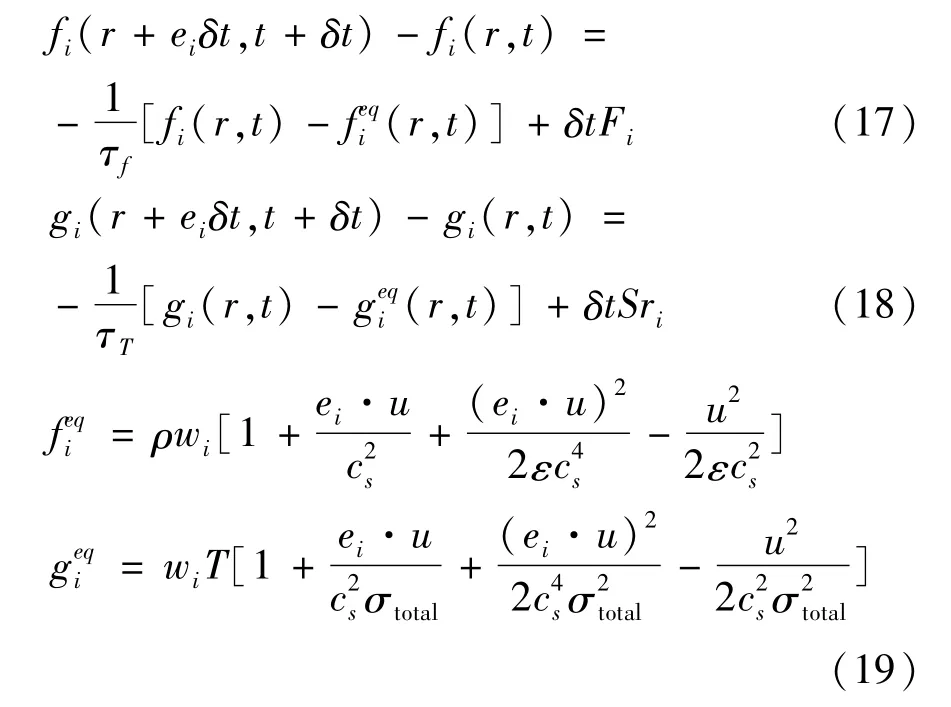
对应源项 Fi、Sri分别由式（20）、（21）表示为

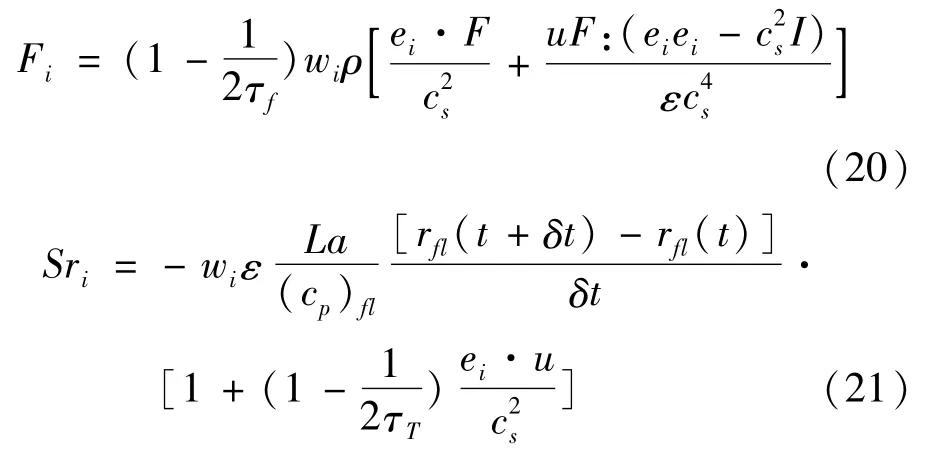
式中：F由式（4）表示；速度与温度演化方程中无量纲松弛时间由确定。

宏观密度和速度由式（19）统计求和为

3 固液相变数学模型的求解和验证

在目前的相变过程研究中，无填充多孔介质腔体内有糊状区的固液相变过程没有公认的基准解。为了验证两区域焓多孔介质的LBM模型的正确性，对方腔内填充满均匀介质的有固定熔化温度（比如镓熔点为29.93℃）的相变材料进行模拟研究。取尺寸高×宽 ＝H×H的方腔，初始时刻，方腔内部充满温度θc为0，融化温度θm为0的固体相变材料，并设此相变材料的相变半径θR为0。数值模拟过程中，方腔左侧保持无量纲温度θh＝1，上下壁面为绝热壁面。现阶段模型的验证广泛使用Jany等提出的左壁面平均Nu数的关联式作为基准解，由式（23）［6］表示为

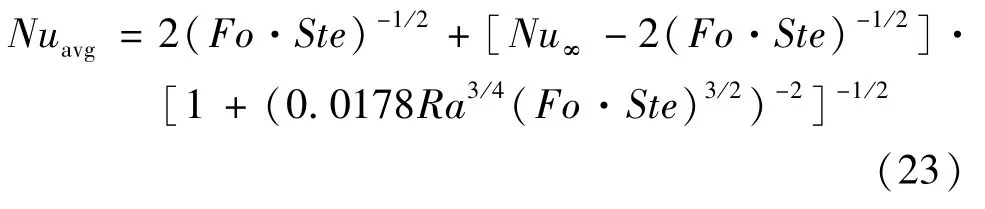
式中：Nu∞采用Benard等的计算公式Nu∞＝0.33 Ra1／4［20］。

选用Pr＝10.0和 Ste＝0.1，Ra数分别选取1×104、1×105、1×106等3种工况模拟方腔内纯相变材料融化过程。选取孔隙率ε分别为0.4和0.6，Da数分别选取1×10-4和1×10-2、Ra＝1×105、Pr＝1，模拟多孔介质方腔中的自然对流。同时，在保证计算结果的网格无关性前提下，获得纯相比3种工况下左壁面平均Nu数随Fo·Ste的变化的数值模拟结果与关联式（23）的基准解进行了对比，如图3所示。多孔介质内自然对流模型和文献［21］的计算结果对比，见表1。由表1可知，数值解和基准解的平均相对误差率均小于1%，验证了此计算方法的正确性。

图3 左壁面平均Nu数的LBM数值解与Jany和Bejan基准解的对比图

表1 方腔内自然对流LBM数值解与经典解的对比结果

4 多孔骨架热物性对固液相变影响结果与分析

4.1 对方腔内无骨架固液相变过程影响

基于两区域模型，采用LBM对无填充多孔介质骨架方腔内的固液相变过程进行模拟研究，选取Fo为0.02、0.04、0.08和 0.4时刻的工况描述其相应的含液率场内的流线分布。当 Pr＝1.0、Ra＝1×106、Ste＝5.0和 θR＝0.10时，选取模拟过程中的 4个Fo对应的含液率分布与流线如图4所示，红色部分表示已融化的相变材料，蓝色部表示未融化的相变材料，而两者之间的颜色表示糊状区（两区域模型的糊状区中高含液率区表现为悬浮液的特点，低含液率区表现为多孔介质内的流动）。图4中相变过程的早期阶段（Fo＝0.002），从液相到固相渐变的不同相变界面几乎相互平行，而其流线几乎垂直于上下的绝热壁面，意味着在初期阶段相变过程的传热方式以导热为主，自然对流换热的影响甚微；由图4（b）～（d）可知，随着融化时间的增加，相变过程的传热方式逐渐由左壁面处的导热为主的传热方式向以自然对流的换热方式为主的方式转换。传热方式以自然对流为主时，方腔上部受热浮升力的影响，导致方腔内上部融化速度大于下部相变材料的融化，从而相变界面发生了一定程度的倾斜。

无填充多孔介质骨架的方腔内相变材料的融化率随时间的变化曲线如图5所示。对比0＜Fo＜0.01和0.01＜Fo＜0.1在融化的初始阶段，相变材料由导热为主的融化速率略大于自然对流为主的融化过程；0.1＜Fo＜0.3时，融化率超过0.6，方腔内相变材料的融化速率逐渐减小；Fo＞0.3时，方腔内的相变材料融化率不再变化，融化的速度近似为零，由图5可以看出，最终融化率维持在0.87。相变过程进入准稳态阶段，方腔内温度、速度不再会随着Fo数变化而变化。在方腔的右壁面处会一直存在部分未融化的相变材料（如图4中的Fo＝0.4所示），是由于右壁面处的低温传热和方腔内的已融化的相变材料的自然对流换热冷热相互抵消，达到一个平衡状态。

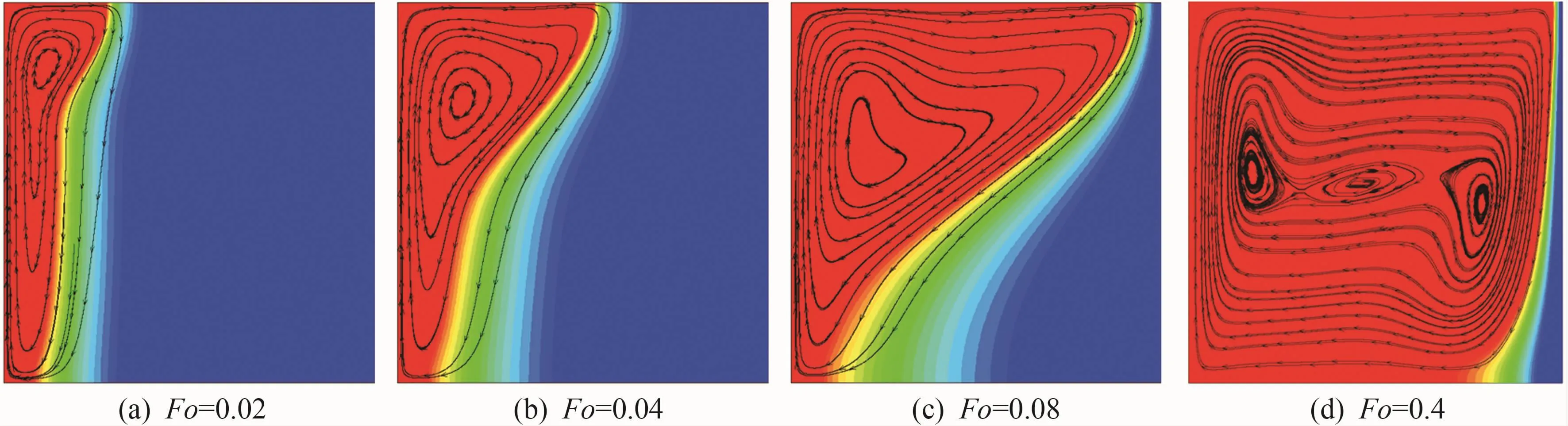
图4 4个Fo对应的含液率分布与流线图

图5 无填充多孔介质骨架的方腔内融化率随时间的变化曲线图

准稳态时的等温线、速度矢量图与含液率分布如图6所示。图6（a）中方腔内的融化受到自然对流的影响，在热浮升力的作用下，方腔的上部空间的流速加快，换热能力加强，融化速度加快，因此在上部靠近冷壁面处的温度梯度大；下部融化速度较慢，融化过程受到抑制，因此糊状区在方腔上部较薄，而在方腔下部较厚。为了进一步展现出糊状区在融化过程的显著影响，图6（b）中含液率rfl分别为0.01、0.5、0.99的等含液率线与图 6（a）中无量纲温度 θ分别为 0.4、0.2、0.1的等温线近似重合，证明了相变过程中糊状区的存在，为建立的两区域模型提供了有力的支撑。

图6 等温线、速度矢量图与含液率分布图（Fo＝0.4）

4.2 对方腔内有骨架的固液相变过程影响

对图1所示的填充多孔介质骨架（孔隙率为0.8889）的固—液相变过程，两区域模型模拟孔隙尺度上不同导热系数骨架对相变过程的影响。相变过程融化率随时间的变化如图7所示，多孔骨架导热系数的变化对于相变过程中的融化速率、融化率影响显著。从图7可以看出：Fo＜0.05时，在融化的初始阶段，高导热系数的骨架的加入会明显促进靠近热壁面处的融化；随着骨架的导热系数的增加对融化有明显的促进效果，并且导热系数越大，越能促进融化。0.05＜Fo＜0.25时，融化进行到中期，由于多孔骨架的加入会在一定程度上抑制方腔内的自然对流强度，此时的融化过程的自然对流换热流动受到多孔骨架的阻碍作用增强，对流换热作用减弱；而不同骨架的导热系数越大，越能促进相变材料的融化。在Fo＞0.25时达到准稳定状态，此时相变材料不再融化，多孔骨架的加入会明显降低方腔内相变材料的融化率；同时，由于多孔骨架导热系数的增加对在冷壁面附近自然对流换热起到抑制作用，导致在准稳态阶段骨架的导热系数增高，其相应融化率的降低。

方腔内无骨架和不同导热系数骨架的含液率分布与流线如图8所示，相变过程达到准稳态阶段（Fo＝0.4）。由图8（b）～（f）可以看出在方腔内的右上部，随着填充多孔骨架导热系数的增加，导热系数越高越能促进自然对流换热，导致上部位置的糊状区速度越大且糊状区面积越薄，方腔右上部未融化的相变材料越来越薄。在方腔内的右下部，随着填充的多孔骨架导热系数的增加，糊状区下部位置的速度受到抑制越来越大，靠近右壁面的糊状区越来越厚，方腔右下部未融化的相变材料也越来越厚。探究其原因：方腔内的自然对流产生热浮升力加快了上部对流换热强度，从而导致方腔内的上部糊状区所占体积较小；多孔骨架导热系数越大，糊状区的热量传递到右侧冷壁面的速度越快，使得糊状区的下部区域面积随着骨架导热系数的增加而增加，整个方腔内的融化率也会相应降低。

图7 融化率随时间的变化图

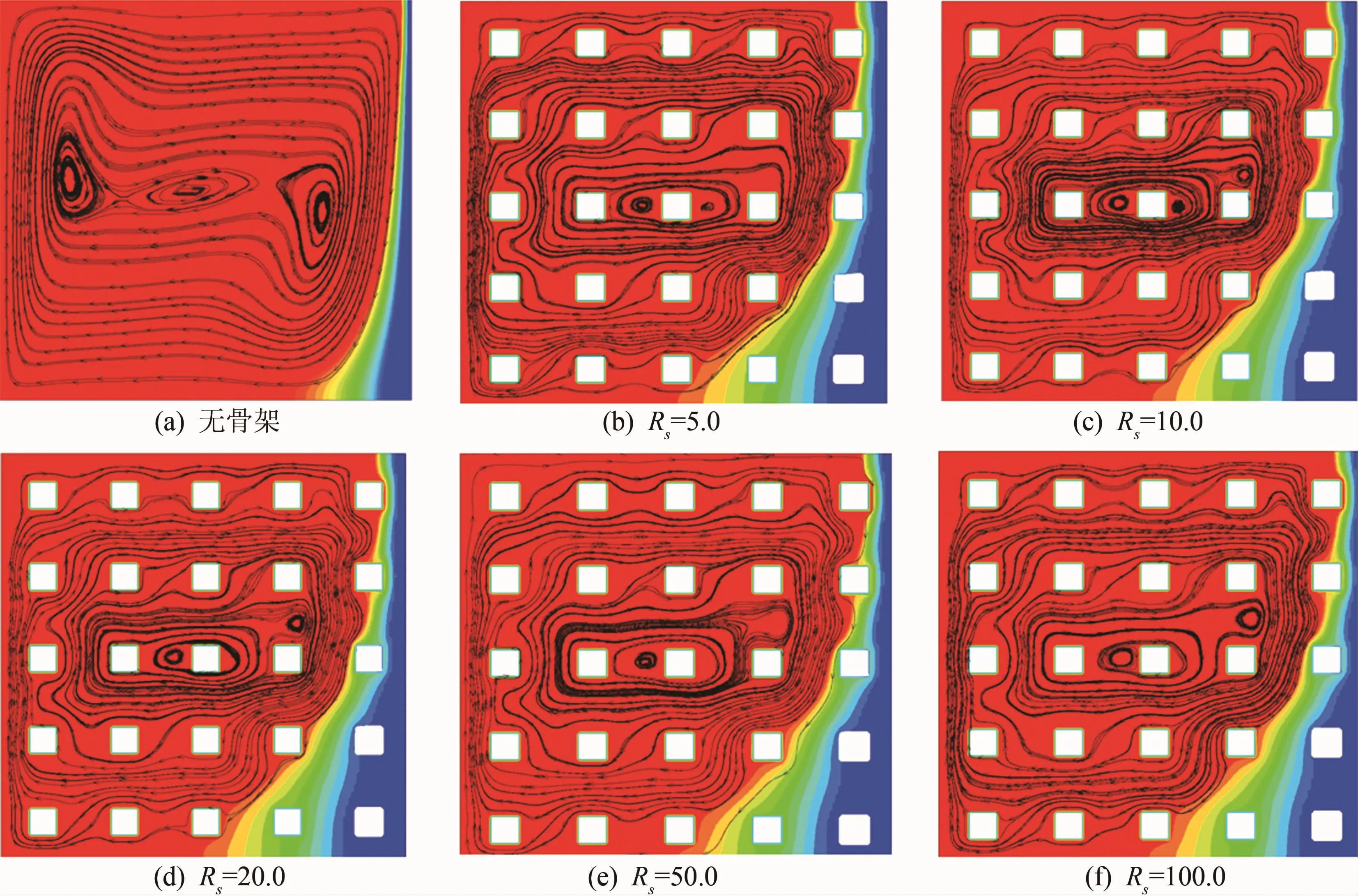
图8 方腔内无骨架和不同导热系数骨架的含液率分布与流线图（Fo＝0.4）

Y＝1／2高度处不同导热系数骨架的速度分布（Fo＝0.4）的变化如图9所示，在靠近右壁面处的位置（X＝0.05），随着导热系数的增加，靠近热壁面处y轴方向的速度越大。由图9可知，对应的自然对流作用越强，高导热系数骨架促进传热越明显；无骨架的y轴方向的速度大于有骨架的速度，说明靠近热壁面处的骨架的存在抑制自然对流的作用大于其高导热系数的促进作用。与之相反的是靠近冷壁面处，其导热系数越大，其对应y轴方向的速度越小，自然对流作用越弱，导致相变过程的融化减弱，糊状区的厚度也就会相应增加。综合冷热壁面处的工况，可知骨架的存在会明显削弱对流换热强度，与图8的描述相吻合。

平均Nu数反映壁面处的换热能力的大小，如图10所示，无论何种工况，在相变融化的初始阶段，都会有一个明显的下降，这是由于在相变的初始阶段存着在相变导热为主的传热方式向自然对流换热方式为主的传热方式的转换。在相变的阶段（Fo＜0.25），有无多孔骨架对于左壁面平均Nu数影响显著，有骨架的左壁面平均Nu数会明显低于无骨架左壁面平均Nu数；而多孔骨架导热系数的变化对左壁面平均Nu数影响不大。准稳态阶段（Fo＞0.25）时，由于骨架对自然对流换热传热的抑制作用明显，填充不同导热率系数骨架的左壁面平均Nu数明显低于无填充多孔骨架的Nu数；在局部放大图中可知，随着骨架导热系数增加，壁面平均Nu数会相应增加。

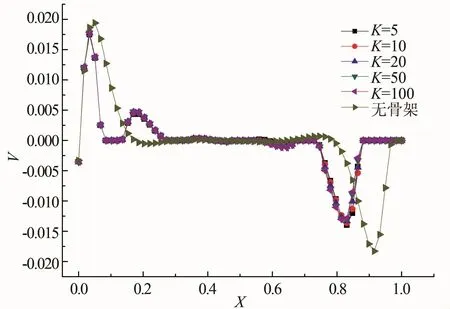
图9 Y＝1／2高度处不同导热系数骨架的速度分布图（Fo＝0.4）

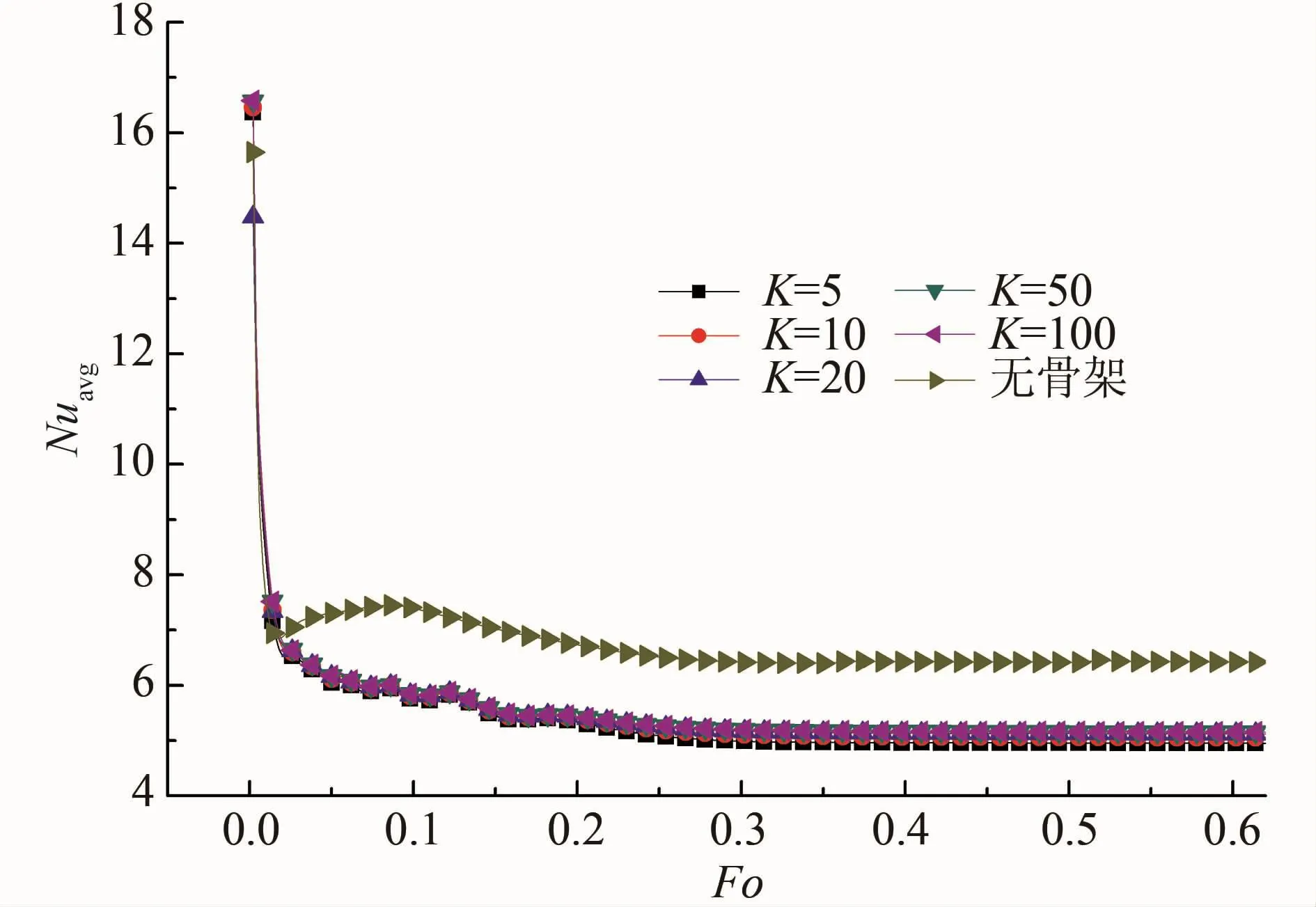
图10 左壁面平均Nu数随时间的变化图

5 结论

采用两区域模型，利用格子玻尔兹曼方法LBM对方腔内固液相变过程进行研究表明：

（1）对于无填充多孔介质骨架方腔内的固液相变过程，传热主导由热传导逐渐向自然对流换热转变，导致了向右倾斜的糊状区。当Fo数大于0.25时，方腔内的融化率不再变化，表示相变过程进入准稳态阶段。

（2）无填充多孔介质骨架方腔内糊状区的存在对相变过程中的速度场有比较显著的影响。由于自然对流的换热方式为主，方腔内相变过程上部融化速度大于下部相变材料的融化，从而糊状区发生了一定程度的倾斜，并且由于自然对流中热浮升力对糊状区的影响，会导致方腔内上部糊状区较薄，而下部糊状区较厚。进入准稳态阶段，由于糊状区的存在，相变材料不会完全融化，在方腔内的左侧壁面处会存在一个上窄下宽的未融化相变材料。

（3）填充多孔骨架导热系数的不同对相变过程影响显著。相变材料蓄热阶段（Fo＜0.05）时，高导热系数多孔骨架会显著促进相变材料的融化，此时导热系数越大，融化率越高，并且随着相变过程的进行，腔体内的多空骨架阻碍自然对流作用（0.05＜Fo＜0.25），此时相变材料的融化率增大效果并不明显；准稳态阶段（Fo＞0.25）时，相变材料的融化率保持不变，腔体内填充的高导热系数的多孔骨架对自然对流换热有明显的抑制作用，最终导致方腔内的左壁面处的未融化部分随导热系数增大而增大。

［1］ Hed G.，Bellander R..Mathematicalmodelling of PCM air heat exchanger［J］.Energy Buildings，2006，38（2）：82-89.

［2］ Gosselin L.，lacroix M..Heat transfer and banks formation in a slag Bath with embedded heat sources［J］.International Journal of HeatMass Transfer，2003，46（14）：2537-2545.

［3］ Zhang Z.，Fang X..Study on paraffin／expanded graphite composite phase change thermalenergy storagematerial［J］.Energy Conversion and Management，2006，47（3）：303-310.

［4］ Trp A..An experimental and numerical investigation of heat transfer during technical grade paraffin melting and solidification in a shellandtube latent thermal energy storage unit［J］.Solar Energy，2005，79（6）：648-660.

［5］ Kazmierczak M.，Poulikakos D.，Pop I..Melting from a flat plate embedded in a porous medium in the presence of steady natural convection［J］.Numerical Heat Transfer Applications，1986，10（10）：571-581.

［6］ Jany P.，Bejan A..Scales ofmelting in the presence of natural convection in a rectangular cavity filled with porousmedium［J］.Journal of Heat Transfer，1988，110（2）：526-529.

［7］ Bejan A..Theory ofmelting with natural convection in an enclosed porousmedium［J］.Journal of Heat Transfer，1989，111（2）：407-415.

［8］ Mancin S.，Diani A.，Doretti L.，et al..Experimental analysis of phase change phenomenon ofparaffin waxesembedded in copper foams［J］.International Journal of Thermal Sciences，2015，90：79-89.

［9］ 何叶从，周杰，王厚华，等.相变墙房间传热特性研究［J］.太阳能学报，2007，28（10）：1085-1090.

［10］崔娜，谢静超，刘加平，等.石膏基相变储能构件的数值模拟分析［J］.化工学报，2014，65（s1）：328-335.

［11］Wen S.，Jiaung C.K..Lattice boltzmann method for the heat conduction problem with phase change［J］.Numerical Heat Transfer Fundamentals，2001，39（2）：167-187.

［12］夏莉.复合相变储能材料的研制与潜热储能中热物理现象的研究［D］.上海：上海交通大学，2011.

［13］ Gao D.，Chen Z..Lattice boltzmann simulation of natural convection dominated melting in a rectangular cavity filled with porous media［J］.International Journal of Thermal Sciences，2011，50（4）：493-501.

［14］Voller V.R.，Prakash C.A..Fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems［J］.International Journal of Heat and Mass Transfer，1987，30（8）：1709-1719.

［15］Mehrabian R.，Keane M.，Flemings M.C..Interdendritic fluid flow and macrosegregation influence of gravity［J］.Metallurgical and Materials Transactions B，1970，1（5）：1209-1220.

［16］ Hu X.，Zhang Y..Novel insight and numerical analysis of convective heat transfer enhancementwithmicroencapsulated phase change material slurries：Laminar flow in a circular tube with constant heat flux［J］.International Journal of Heat and Mass Transfer，2002，45（15）：3163-3172.

［17］GoelM.，Roy S.K.，Sengupta S..laminar forced convection heat transfer in microcapsulated phase changematerial suspensions［J］.International Journal of Heat and Mass Transfer，1994，37（4）：593-604.

［18］Bhattacharya M.，Basak T.G..A fixed-grid finite element based enthalpy formulation for generalized phase change problems：role of superficialmushy region［J］.International Journal of Heat and Mass Transfer，2002，45（24）：4881-4898.

［19］柴振华，郭照立，施宝昌.用多松弛格子Boltzmann方法预测多孔介质的渗透率［J］.工程热物理学报，2010，31（1）：107-109.

［20］Bertrand O.，Binet B.，Combeau H.，et al..Melting driven by natural convection——A comparison exercise：first results［J］.International Journal of Thermal Sciences，1999，38（1）：5-26.

［21］Seta T.，Takegoshi E.，Okui K..Lattice Boltzmann simulation of natural convection in porous media［J］.Mathematics and Computers in Simulation，2006，72（2）：195-200.

（学科责编：赵成龙）

Research on the influence of solid liquid phase change in porous skeleton media based on LBM method

Song Linquan1，Chen Baoming1，2，3，*，Gao Kaikai1
（1.School of Thermal Engineering，Shandong Jianzhu University，Jinan 250101，China；2.Key Laboratory of Renewable Energy Utilization Technology in Building of National Education Ministry，Shandong Jianzhu University，Jinan 250101，China；3.Shandong Key Laboratory of Building Energy-Saving Technologies，Shandong Jianzhu University，Jinan 250101，China）

TU996

A

1673-7644（2017）04-0356-09

2017-06-18

宋林泉（1990-）男，在读硕士，主要从事多孔介质内流动换热等方面的研究.E-mail：923344348＠qq.com

*：陈宝明（1963-）男，教授，博士，主要从事复杂体系中的传热传质等方面的研究.E-mail：chenbm＠sdjzu.edu.cn