双曲线型钢结构冷却塔缺陷敏感性分析

朱俊颖, 吴 杰, 张其林

(同济大学 土木工程学院, 上海200092)

双曲线型钢结构冷却塔缺陷敏感性分析

朱俊颖, 吴 杰, 张其林

(同济大学 土木工程学院, 上海200092)

参考国内现有规范, 考虑几何非线性与材料非线性, 利用ANSYS软件对一座高150 m的双曲线型钢结构冷却塔进行多种缺陷及多缺陷值下的稳定计算, 讨论了单层网壳、双层网壳及不同网格形式下结构的缺陷敏感性. 结果表明, 单层网壳结构对某些缺陷敏感性高, 双层网壳结构中采用三角形网格时的稳定系数最高, 四角锥网格的缺陷敏感性最低.

钢结构冷却塔; 缺陷敏感性; 双非线性; 有限元分析

冷却塔是火力发电厂用于降低乏汽温度的构筑物[1], 一般而言, 塔越高, 冷却效果越好, 发电效率越高[2]. 世界上第一座冷却塔于1915年建于荷兰, 为高45 m的钢筋混凝土结构; 1964年, Hitkamp公司在德国首次建造了高100 m的冷却塔; 我国的冷却塔建造起步较晚, 1973年在山东兴店电厂建造了首座高90 m的大型冷却塔[1]. 随着人们对能源需求的不断增加, 冷却塔不断向着大型化的方向发展. 2001年, 高达200 m的超大型冷却塔在德国Niederaussem的RWE发电厂建成[3]. 目前, 世界上大多数冷却塔为钢筋混凝土结构, 而钢结构冷却塔由于其结构轻巧、塔内空气阻力小、施工周期短的特点[4], 逐渐受到研究者的关注, 但研究远未成熟. 20世纪80年代, 苏联和伊朗建立了高120 m的钢网格结构冷却塔[5], 之后研究者们通过对钢结构冷却塔进行结构静力分析、结构整体稳定性分析以及结构动力响应分析等, 验证了钢结构冷却塔的可行性[6-11]. 然而, 目前仍缺乏钢结构冷却塔的缺陷敏感性研究.

本文以一座高150 m的双曲线型冷却塔为例, 分别对其在单层网壳、双层网壳及不同网格形式下进行双非线性有限元分析, 即同时考虑几何非线性与材料非线性的有限元分析, 讨论了钢结构冷却塔在不同缺陷分布及缺陷大小下的稳定性, 为今后的双曲线型钢结构冷却塔的稳定计算提供参考.

1 计算模型与荷载

1.1计算模型

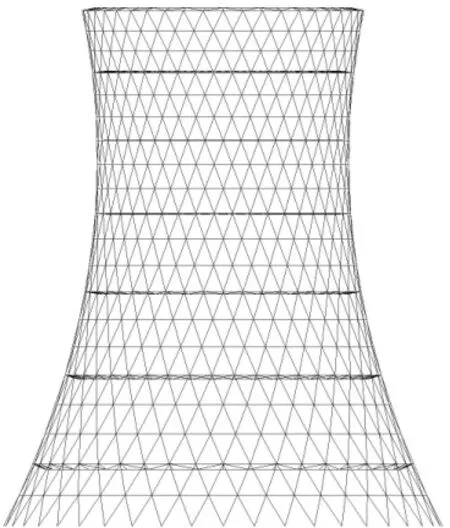
(a) 单层网壳

钢结构冷塔高度为150 m, 出口直径为82.3 m, 喉部高度为112.7 m, 喉部直径为72.2 m, 底部直径为124.9 m, 钢结构冷却塔塔型示意图如图1所示. 为考虑不同结构体系与网格形式下钢结构冷却塔的稳定性, 设计多种钢结构冷却塔方案列于表1中, 其中包括各模型中杆件应力比及杆件截面范围, 所有杆件均为圆管截面.钢结构冷却塔的不同网格形式如图2所示, 其中单层网壳模型中布置7个肋. 使用满应力法进行结构优化设计, 通过调整各模型的应力比, 使其用钢量基本相同, 以此消除用钢量对结构稳定性的影响.

(b) 双层网壳图1 钢结构冷却塔塔型Fig. 1 Configuration of steel cooling tower

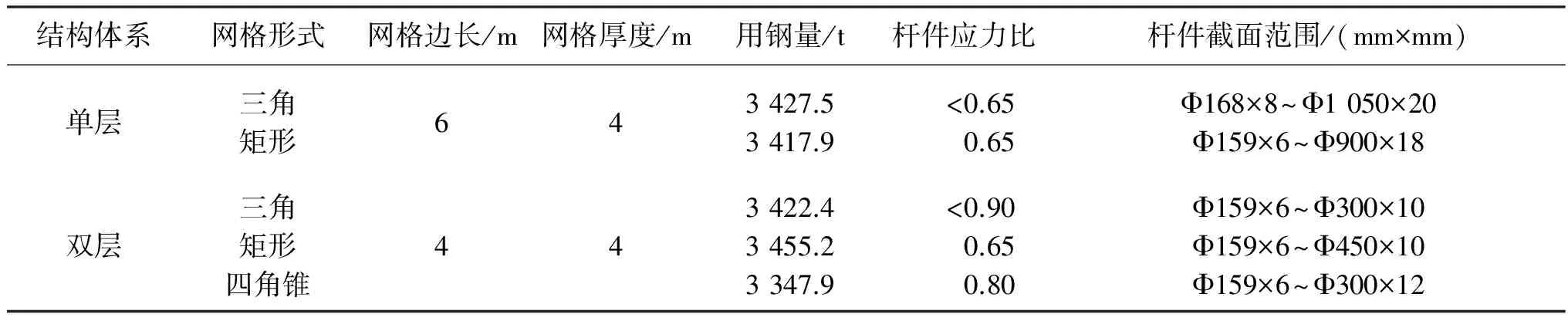
结构体系网格形式网格边长/m网格厚度/m用钢量/t杆件应力比杆件截面范围/(mm×mm)单层三角矩形643427．53417．9<0．650．65Φ168×8～Φ1050×20Φ159×6～Φ900×18双层三角矩形四角锥443422．43455．23347．9<0．900．650．80Φ159×6～Φ300×10Φ159×6～Φ450×10Φ159×6～Φ300×12

(a) 单层三角

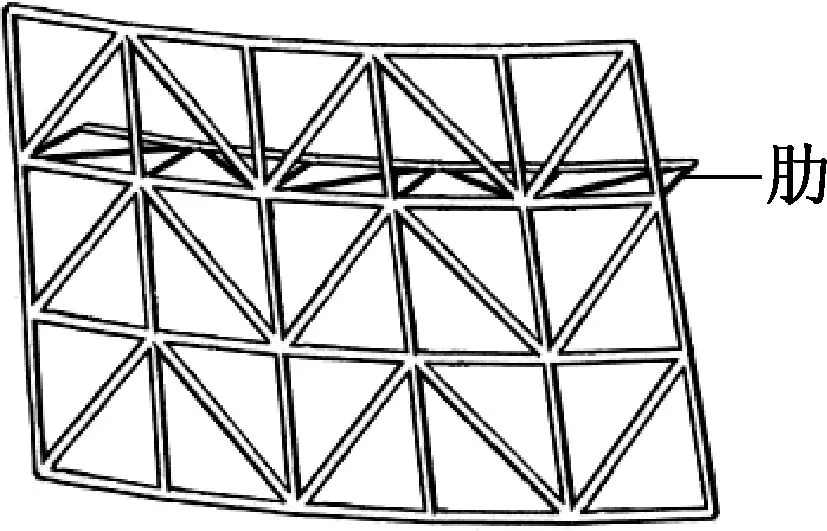
(b) 单层矩形

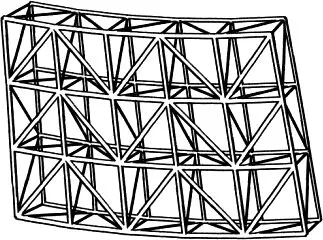
(d) 双层矩形

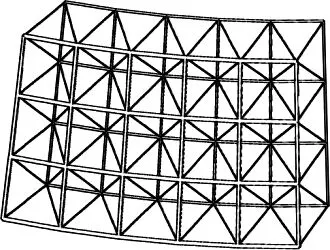
(e) 双层四角锥

1.2荷载

冷却塔受到的荷载有恒载、外风荷载、塔内风吸荷载、温度作用、地震作用. 依据GB/T 50102—2014[12], 稳定分析需考虑恒载和风荷载(包括外风荷载及塔内风吸荷载), 本文未考虑温度作用和地震作用对结构稳定的影响. 恒载包括结构的杆件自重及外挂面板自重, 面板自重按照0.2 kN/m2计算. 风荷载的风振系数为1.9.

2 恒载作用下冷却塔的缺陷敏感性

选定三角形网格形式, 计算单层网壳和双层网壳结构体系下, 结构仅承受恒载时的缺陷敏感性. 通过弹性屈曲分析得到结构的前10阶模态, 利用这些模态进行带缺陷结构的双非线性分析, 选出有代表性的屈曲模态作为缺陷, 分析结构的荷载系数随该缺陷大小变化的规律.

2.1单层网壳

单层网壳模型的线性屈曲荷载系数如表2所示. 由表2可知, 模型的前10阶屈曲荷载系数成对出现, 即第1阶与第2阶、第3阶与第4阶荷载系数基本相同, 以此类推. 考虑到本节分析模型为圆对称模型, 考察其在圆对称荷载下的稳定性, 由于荷载系数相同时屈曲模态基本相同, 其对结构的影响也基本相同, 故取第1、3、5、7、9阶屈曲模态作为缺陷施加于结构, 取缺陷大小为结构高度的±1/300，即±H/300[13], 计算结构的双非线性荷载系数, 计算结果如表3所示.

由表3可知, 对单层网壳模型仅施加恒载(对称荷载)时, 同一缺陷在正向和反向施加于结构后, 对结构产生的影响基本相同. 故取最不利的第1阶屈曲模态(图3)作为缺陷, 取缺陷大小为±H/1000、 ±H/500、±H/300、±H/200, 分析结构的稳定性随缺陷大小变化的规律, 计算结果如图4 和表4所示.

表2 单层网壳模型的线性屈曲荷载系数Table 2 Linear buckling load factor for model with single-layer latticed shell

表3 缺陷大小为±H/300时单层网壳模型的双非线性荷载系数Table 3 Double nonlinear buckling load factor for model with single-layer latticed shell considering an imperfection of ±H/300

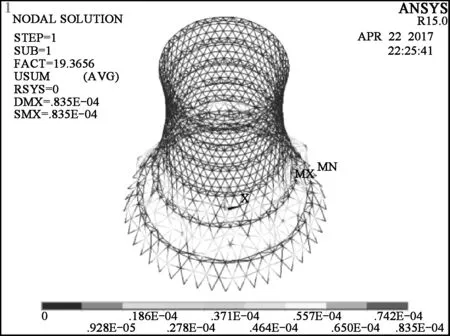
图3 单层网壳模型的第1阶屈曲模态Fig. 3 The first buckling mode of model with single-layer latticed shell

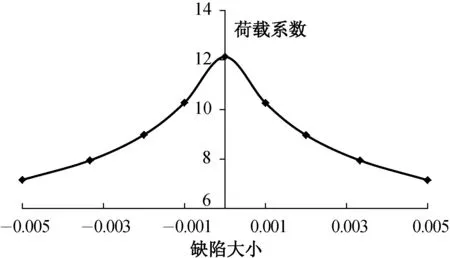
图4 第1阶屈曲模态作为缺陷时单层网壳模型的荷载系数相对缺陷曲线Fig. 4 The curve of load factor to relative defect of structure with single-layer latticed shell taking first buckling mode as imperfection

缺陷大小-H/200-H/300-H/500-H/10000H/1000H/500H/300H/200荷载系数7．157．938．9710．2712．1210．268．967．947．14变化百分比/%-41．02-34．56-26．01-15．290-15．36-26．07-34．53-41．07

综上所述, 对于单层网壳模型, 仅考虑恒载的情况下: 缺陷大小绝对值相同时, 荷载系数基本相同, 故缺陷敏感性类型为“不稳定对称分支点性态”; 当缺陷为H/300时, 单层网壳的荷载系数折减达到原来的34.56%, 结构的缺陷敏感性较高.

2.2双层网壳

双层网壳模型的线性屈曲荷载系数如表5所示. 由表5可知, 模型的前10阶屈曲荷载系数成对出现, 其中第1阶与第2阶、第3阶与第4阶、第5阶与第6阶、第8阶与第9阶的荷载系数基本相同. 考虑到本节分析模型为圆对称模型, 考察其在圆对称荷载下的稳定性, 由于荷载系数相同时屈曲模态基本相同, 其对结构的影响也基本相同, 故取第1、3、5、7、9、10阶屈曲模态作为缺陷施加于结构, 取缺陷大小为±H/300, 计算结构的双非线性荷载系数, 计算结果如表6所示.

表5 双层网壳模型的线性屈曲荷载系数Table 5 Linear buckling load factor for model with double-layer latticed shell

表6 缺陷大小为±H/300时双层网壳模型的双非线性荷载系数Table 6 Double nonlinear buckling load factor for model with double-layer latticed shell considering an imperfection of ±H/300

由表6可知： 对双层网壳模型仅施加恒载时, 除第7阶模态外, 同一缺陷在正向和反向施加于结构后, 对结构产生的影响基本相同; 而按第7阶屈曲模态施加荷载时, 正向与反向施加荷载得到了不同的荷载系数. 故取最不利的第1阶和第7阶屈曲模态(见图5)作为缺陷, 取缺陷大小为±H/1000、±H/500、±H/300、±H/200, 分析结构的稳定性随缺陷大小变化的规律, 计算结果如图6和表7所示.

图5 双层网壳模型的第7阶屈曲模态Fig. 5 The 7th buckling mode for model with double-layer latticed shell

图6 第1阶和第7阶屈曲模态作为缺陷时双层网壳模型的荷载系数相对缺陷曲线Fig.6 The curve of load factor to relative defect of structure with double-layer latticed shell taking the first and seventh buckling modes as imperfection

缺陷大小-H/200-H/300-H/500-H/10000H/1000H/500H/300H/200第1阶荷载系数11．5812．9514．4115．1915．1515．1914．4112．9511．58变化百分比/%-23．56-14．52-4．880．2600．26-4．88-14．52-23．56第7阶荷载系数9．0311．2313．4614．2615．1516．2016．3716．3816．44变化百分比/%-40．40-25．87-11．16-5．8706．938．058．128．51

综上所述, 对于双层网壳模型, 仅考虑恒载的情况下: 按第1阶屈曲模态施加缺陷时, 不论缺陷是正数还是负数, 与无缺陷相比, 其稳定性均下降, 属于“不稳定对称分支点性态”; 按第7阶屈曲模态施加缺陷时, 与无缺陷相比, 缺陷正向施加时结构稳定性提高, 而缺陷反向施加时结构稳定性降低, 属于“非对称分支点稳定性态”; 当缺陷为-H/300时, 双层网壳的荷载系数折减在第1阶和第7阶屈曲模态的缺陷下分别为14.56%和25.86%, 结构的缺陷敏感性相比单层网壳模型较低.

3 恒载和风载共同作用下冷却塔的缺陷敏感性

3.1不同缺陷的敏感性分析

计算表1中的5个模型在恒载和风载共同作用下的结构稳定性, 根据目前的工程经验, 将结构的第1阶屈曲模态和第1阶整体屈曲模态作为缺陷施加于结构, 缺陷大小取H/300, 计算结构的双非线性屈曲荷载系数, 结果如表8所示, 并将经过计算比较后得到的结构前10阶屈曲模态中对结构最不利者列于表8中.

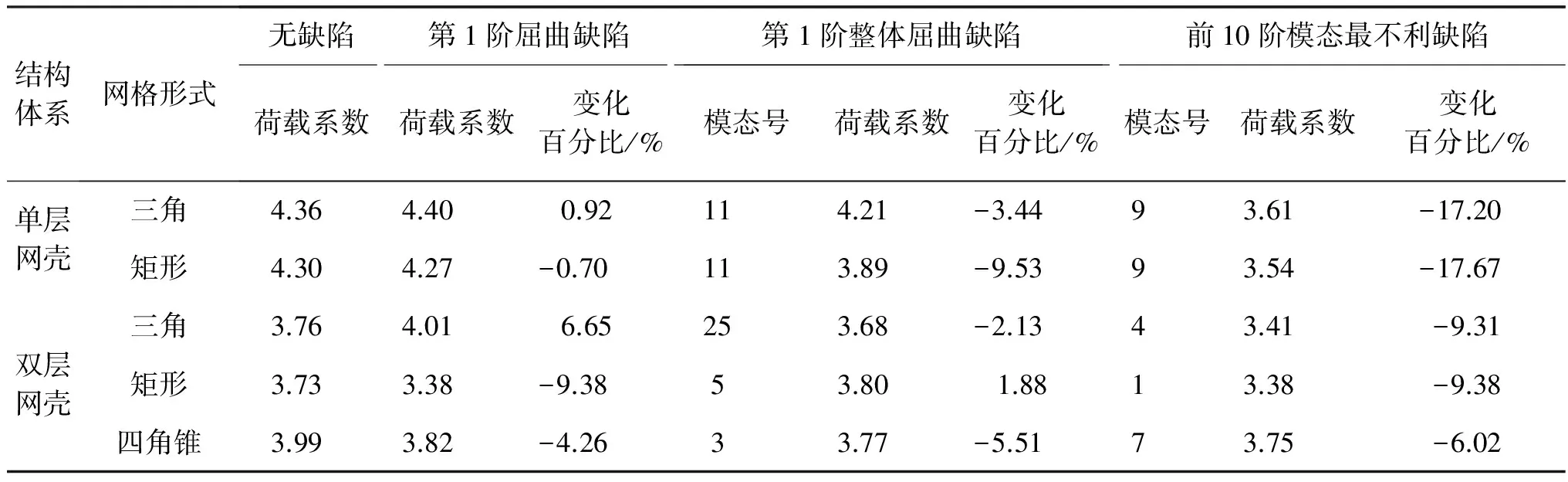
表8 恒载和风载共同作用下不同模型结构的双非线性屈曲荷载系数Table 8 Double nonlinear buckling load factor of different models under both dead load and wind load

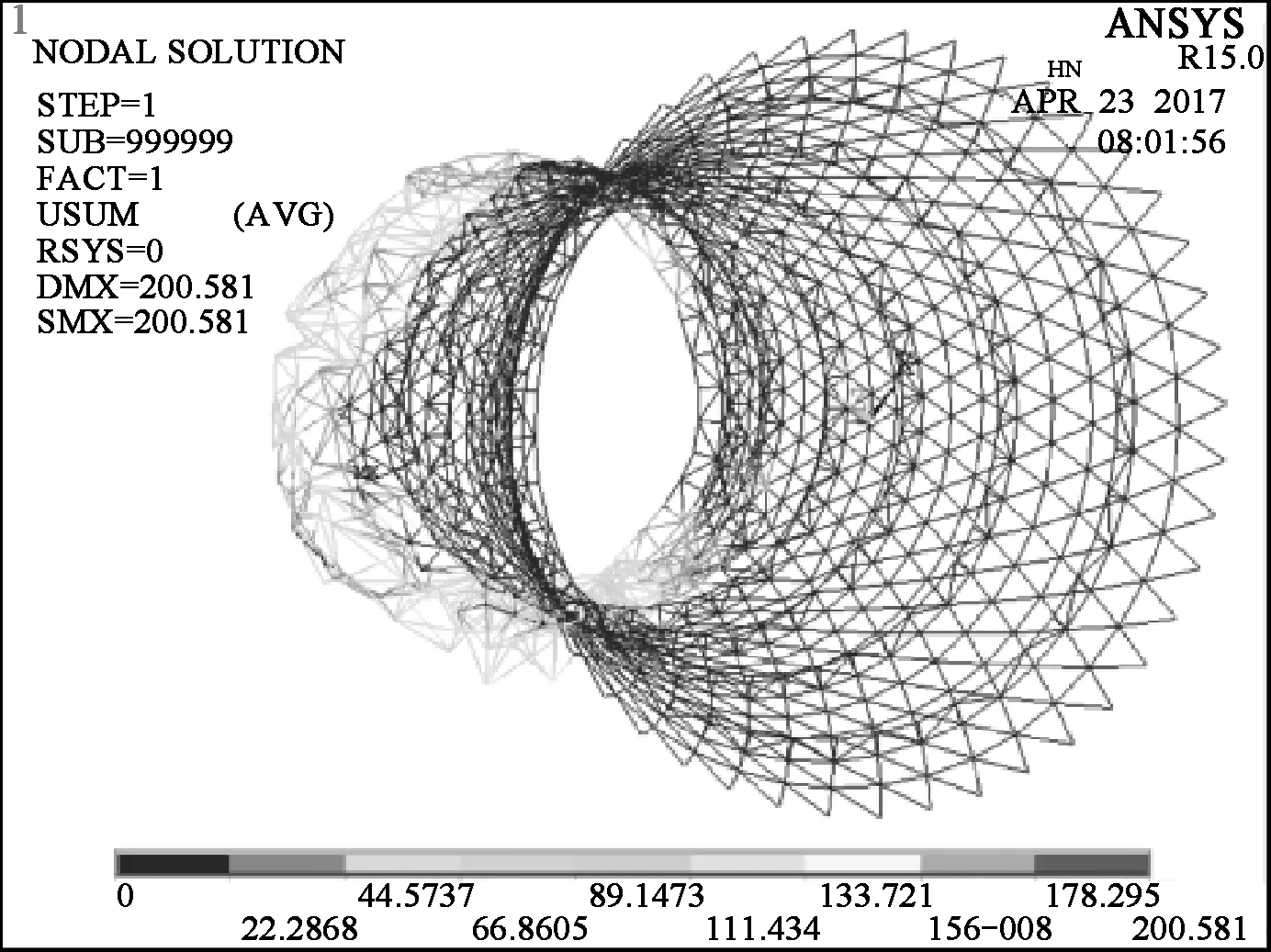
(a) 单层网壳

(b) 双层网壳

由表8可知, 同时考虑恒载和风载的情况下, 对于单层网壳模型: 两种网格形式(三角形和矩形)下, 单层网壳的极限承载力差别不大; 单层网壳模型相对双层, 稳定系数高, 但其对某些缺陷的敏感性较高, 稳定性变化达17%, 同时其失稳区域较大(见图7), 故不建议在高度较大的双曲线型钢结构冷却塔中使用单层网壳. 对于双层网壳模型: 3种网格形式下, 三角形网格的极限承载力最大, 矩形网格的极限承载力最低; 与单层网壳相比, 双层网壳模型的稳定系数较低, 但其在缺陷下的稳定性变化均在10%以内, 缺陷敏感性比单层网壳低, 且失稳区域为单个节点(见图7).

3.2改变缺陷大小的敏感性分析

由于单层网壳结构对某些缺陷的敏感性很高, 故选用单双层网壳模型进行结构敏感性计算分析. 对三角形网格模型, 选择前10阶中最不利缺陷及第1个整体失稳模态, 即第4阶和第25阶屈曲模态; 对矩形网格和四角锥网格的模型, 选择前10阶中最不利缺陷, 即分别采用第1阶和第7阶屈曲模态作为缺陷. 双层网壳模型的不同屈曲模态如图8所示. 取缺陷大小为±H/1000、±H/500、±H/300和±H/200, 分析结构的稳定性随缺陷大小变化的规律.三角形网格模型的稳定性随缺陷大小变化的规律不明显, 缺陷多取±H/400和±H/700, 所得结果如图9和表9所示.

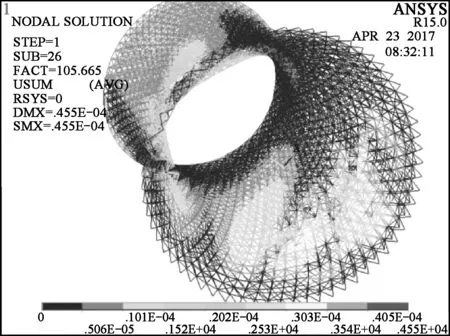
(a) 三角形网格-第25阶屈曲模态

(b) 矩形网格-第1阶屈曲模态

(c) 四角锥网格-第7阶屈曲模态图8 双层网壳模型的屈曲模态Fig.8 Buckling modes of models with double-layer latticed shell

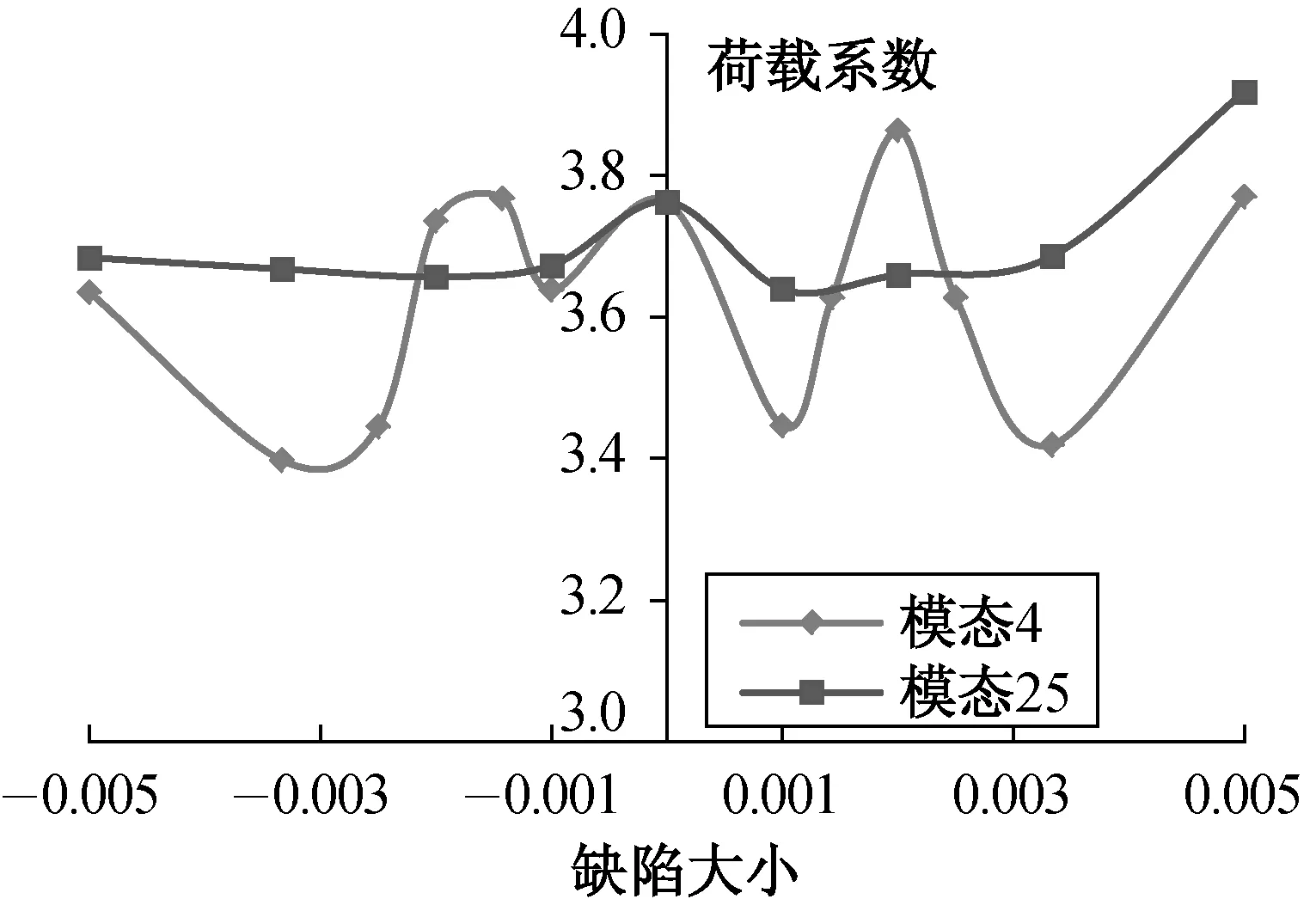
(a) 三角形网格

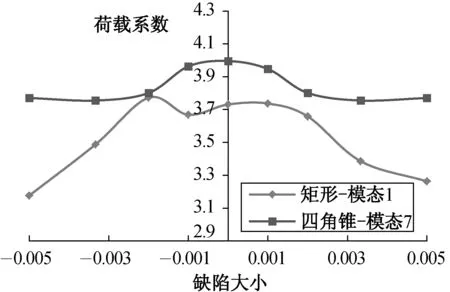
(b) 矩形和四角锥网格

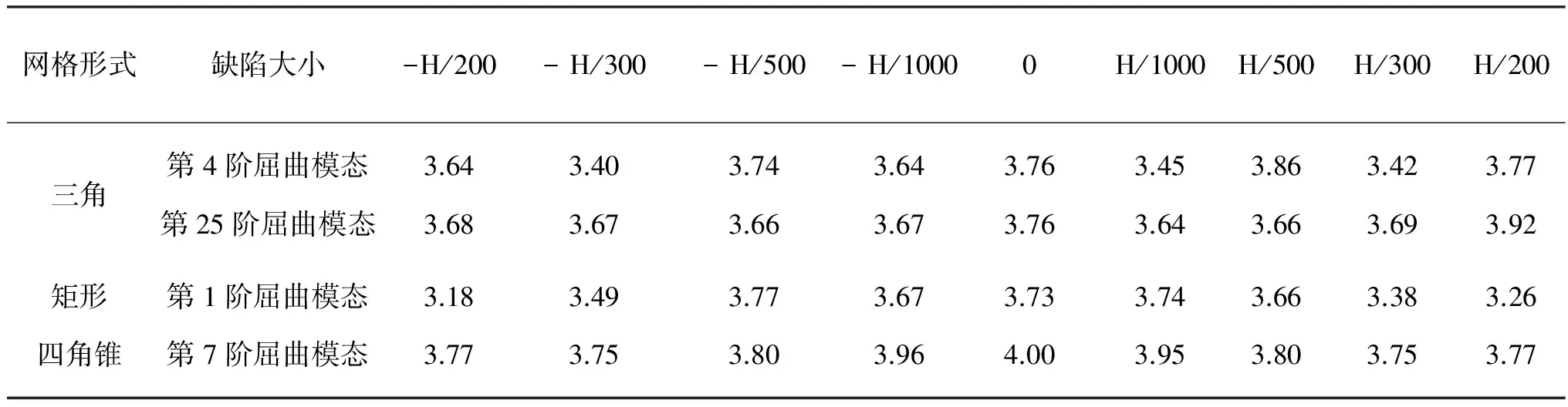
网格形式缺陷大小-H/200-H/300-H/500-H/10000H/1000H/500H/300H/200三角第4阶屈曲模态3．643．403．743．643．763．453．863．423．77第25阶屈曲模态3．683．673．663．673．763．643．663．693．92矩形第1阶屈曲模态3．183．493．773．673．733．743．663．383．26四角锥第7阶屈曲模态3．773．753．803．964．003．953．803．753．77

对于双层网壳三角形网格模型, 可得到以下结论: 在局部缺陷即第4阶屈曲模态下, 其极限承载力随缺陷大小的变化规律不明显, 且呈跳跃的变化特征, 但总体上, 其缺陷敏感性在±10%以内, 好于单层; 在整体缺陷即第25阶屈曲模态下, 其缺陷敏感性的类型为“不稳定对称分支点性态”, 结构对这一整体缺陷的敏感性不高, 荷载系数的变化幅度在4.2%以内.

对于双层网壳矩形和四角锥网格模型, 可得到以下结论: (1)矩形和四角锥两种网格形式对最不利缺陷的敏感性基本符合“不稳定对称分支点性态”的特征；(2)矩形网格下结构对缺陷的敏感性较高一些, 而四角锥网格下结构的缺陷敏感性较低, 且其缺陷敏感性弱于三角形网格, 但从荷载系数绝对值上看, 三角形网格好于四角锥网格.

4 结 语

本文对一座高150 m的钢结构冷却塔在不同网格形式及结构形式下进行双非线性稳定分析, 在各塔型用钢量基本相同以及不考虑温度作用和地震作用的前提下, 得出以下结论:

(1) 采用单层网壳时, 在恒载作用及恒载和风载共同作用的情况下, 其缺陷敏感性均较高. 因此, 对150 m及以上的钢结构冷却塔不建议采用单层网壳.

(2) 采用双层网壳时, 结构的缺陷敏感性表现与结构的网格形式关系较大, 其中三角形网格下结构对某些缺陷的敏感性随缺陷大小变化的规律不明显, 但总体上变化幅度在±10%以内. 在实际计算中, 建议将前10阶或更多屈曲模态均考虑在内, 并同时考虑缺陷大小为1/300和-1/300的情况.

(3) 采用双层网壳时, 四角锥网格下结构的缺陷敏感性最低. 但从荷载系数的绝对值上看, 三角形网格依旧好于四角锥网格. 建议钢结构冷却塔采用双层网壳, 且以三角形网格或四角锥网格作为结构的网格形式.

[1] 柯世堂, 侯宪安, 姚友成, 等. 大型冷却塔结构抗风研究综述与展望[J]. 特种结构, 2012, 29(6): 5-10.

[2] 赵振国. 冷却塔[M]. 北京: 中国水利水电出版社, 1996: 1-6.

[3] BUSCH D, HARTE R, KRTZIG W B, et al. New natural draft cooling tower of 200 m of height[J]. Engineering Structures, 2002, 24(12): 1509-1521.

[4] 叶明国. 冷却塔塔体结构的分析[J]. 化工装备技术, 1998, 19(2) : 15-17.

[6] 尹麟. 大型钢结构双曲抛物面冷却塔探索[J]. 特种结构, 2005, 22(2) : 41-43.

[7] 刘万里, 冯峰, 王吉特, 等. 钢结构干式冷却塔研究[J]. 钢结构, 2011, 26(12): 25-28.

[8] 王金. 大型钢结构自然通风冷却塔的受力分析[D]. 南昌: 华东交通大学土木建筑学院, 2013: 26-31

[9] IZADI M, BARGI K. Natural draft steel hyperbolic cooling towers: Optimization and performance evaluation[J]. Structural Design of Tall & Special Buildings, 2014, 23(9): 713-720.

[10] 乐威, 赵立. 钢结构间接空气冷却塔设计方法研究[J]. 钢结构, 2015, 30(5): 52-55.

[11] 陈珂. 钢结构双曲线冷却塔计算分析及探索[J]. 广东建材, 2015, 31(8) : 49-51.

[12] 中国电力工程顾问集团东北电力设计院.工业循环水冷却设计规范: GB/T 50102-2014[S]. 北京: 中国计划出版社, 2014.

[13] 中国建筑科学研究院.空间网格结构技术规程: JGJ7-2010[S]. 北京: 中国建筑工业出版社, 2010.

(责任编辑:杨静)

ImperfectionSensitivityAnalysisofHyperbolicSteelCoolingTowers

ZHUJunying,WUJie,ZHANGQilin

(College of Civil Engineering, Tongji University, Shanghai 200092, China)

According to the existing domestic codes, stability analysis of a 150 m high hyperbolic steel cooling tower, with different kinds of imperfection and different values of imperfection, is made by ANSYS software, considering both geometry and material nonlinearity. Thus, the imperfection sensitivity of steel cooling towers with single-layer and double-layer latticed shell and different grid forms is analyzed. The results show that the imperfection sensitivity of single-layer latticed shell is high, the double-layer latticed shell, with triangle mesh structure has the highest buckling load factor, and structure with square pyramid mesh has the lowest imperfection sensitivity.

steel cooling tower; imperfection sensitivity; double nonlinearity; finite element analysis

TU 393.3

A

1671-0444 (2017)04-0585-07

2017-04-25

朱俊颖(1994—)，男，湖北武汉人，硕士研究生，研究方向为钢结构和空间结构. E-mail： 554976101@qq.com

吴 杰(联系人)，男，副教授，E-mail： wj536@163.com