基于GA-ELM数控铣刀寿命预测模型研究

周亚勤， 杨建国， 刘凯强， 尤 祥

(东华大学 机械工程学院， 上海 201620)

基于GA-ELM数控铣刀寿命预测模型研究

周亚勤， 杨建国， 刘凯强， 尤 祥

(东华大学 机械工程学院， 上海 201620)

在加工过程中，刀具磨损状况对零件的加工质量具有重要影响，精确预测刀具寿命是智能制造系统必须具有的关键功能之一．在分析数控铣刀寿命影响因素的基础上，引入极限学习机(ELM)算法模型，建立数控铣刀寿命预测模型．在寿命预测过程中，采用遗传算法(GA)对ELM模型的输入权值和隐含层阈值进行优化，建立基于GA-ELM的数控铣刀寿命预测模型，同时将其与基本BP神经网络、优化BP神经网络和基于粒子群改进的BP神经网络的预测结果进行对比分析．结果表明，基于GA-ELM的刀具寿命预测模型相比较于其他3种算法更加优越，是一种行之有效且精度高的刀具寿命预测算法．

刀具寿命； 遗传算法(GA)； 极限学习机(ELM)

新刀由开始使用到破损报废所经历的切削时间累加之和为刀具总寿命[1]，期间包括多次刃磨．在零件加工过程中，刀具磨损状况对其加工质量具有重要影响，精确预测刀具寿命是智能制造系统必须具有的关键功能之一．早期对刀具寿命预测主要是根据泰勒公式，该方法虽然计算简单，但是公式中的参数需要大量实验得出．随着在线监测技术的越发完善，刀具在线监测技术[2]得到了广泛的应用．刀具在线监测技术虽然具有实时、便捷等优点，但无法精准地判定刀具破损时间，容易使机床与工件受损．近年来随着人工智能的越发成熟，智能算法在机械行业之中得到广泛使用[3]，一些专家、学者采用BP(back propagation)神经网络、支持向量机、RBF(radial-basis function)神经网络等方法进行刀具寿命的预测，但是上述方法也存在一定的局限性.如BP神经网络在求解过程中容易陷入局部最优解，网络结构的确定相对困难[4]；支持向量机的参数不易确定[5]； RBF神经网络对训练样本的要求比较高，训练难度较大[6]．针对上述问题，本文采用Huang 等[7-8]提出的极限学习机(ELM)算法作为铣刀寿命预测模型. ELM作为一种新型前馈神经网络，与传统的单隐层神经网络比较，其具有泛化能力强、学习速度快、训练样本少等诸多优点．为了克服模型输入权值及隐含层阈值随机取值对预测模型精度造成的影响，采用遗传算法(GA)对其进行优化，提出基于GA-ELM的数控铣刀寿命预测模型，实现对数控车间铣刀寿命的有效预测．

1 刀具寿命影响因素分析

在实际加工环境下，刀具寿命定义为刀具从开始使用到钝磨所经历的切削时间，用刀具耐用度表示[9]．对刀具寿命进行预测管理，则需分析加工过程中影响刀具耐用度的各种因素．在铣镗钻类数控机床或者加工中心高速切削加工过程中，通过实践经验以及切削试验可以推导出刀具使用寿命T[10]的计算式为

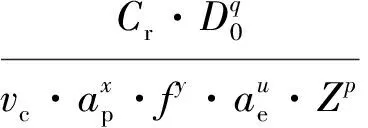
(1)

式中：Cr为刀具寿命的系数，主要与刀具材料、被加工工件材料以及切削方式等有关；Z、ae、f、ap、vc、D0分别为铣刀齿数、铣削宽度、每齿进给量、铣削深度、铣削速度以及铣刀直径；上标p、u、y、x、q分别为各参数对应的指数，大小通常由经验决定．

同时，工件材料对刀具寿命也有很大影响，考虑工件的硬度、塑性、强度等物理性能，同一材质的刀具加工硬度小的工件通常要比加工硬度大的工件更容易，相应刀具的使用寿命也就越长．由于工件材料为非数值量，为了将其作为预测模型的输入参数，采用工件可加工性(Kv)概念对其进行量化处理．Kv强调工件材料的加工难易程度，针对容易切削材料，可加工性较高；针对难切削材料，可加工性较低．表1列出了工件材料的加工难易程度及对应的Kv取值范围．

综上分析，本文考虑铣刀直径、铣刀齿数、每齿进给量、铣削速度、铣削深度、铣削宽度以及工件材料可加工性等因素对刀具寿命的影响，建立这些因素影响下的刀具寿命预测模型．

2 数控铣刀寿命预测模型建立

2．1基于ELM的数控铣刀寿命预测模型建立

ELM模型拓扑结构图如图1所示，该模型由输入层、隐含层、输出层3部分构成．利用ELM建立刀具寿命预测模型，输入层由7个神经元组成，分别对应为铣刀直径、齿数、铣削深度、铣削宽度、进给量、铣削速度、工件可加工性．设隐含层神经元的个数为L，由文献[11]可知，当隐含层与输入层神经元个数一致时，网络模型的预测精度更好，所以本模型设L=7．在本预测模型中，输出结果表示铣刀寿命预测值，所以令输出层神经元个数为1，即表示铣刀寿命预测值．

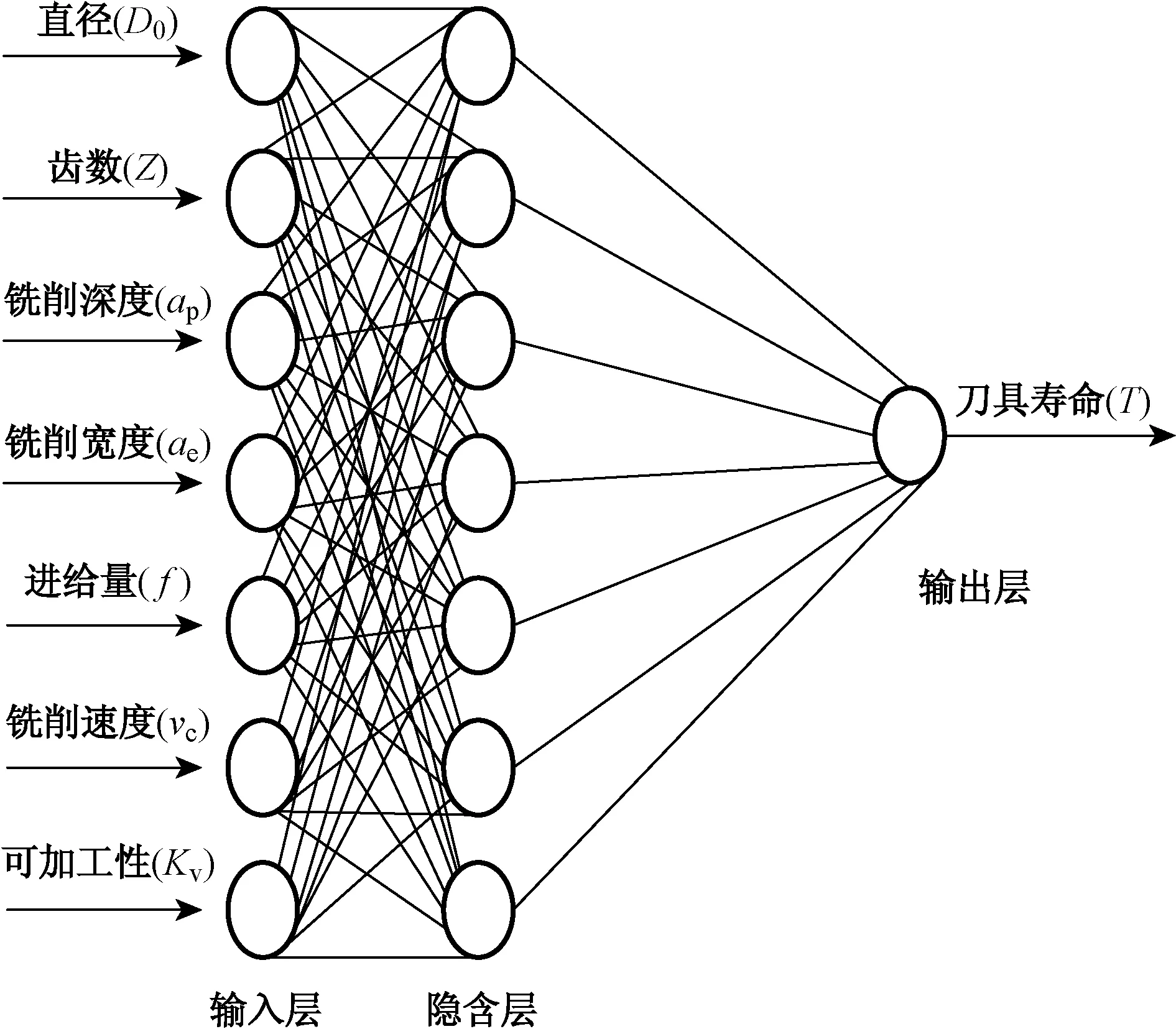
图1 ELM模型拓扑结构图Fig．1 Structure diagram of ELM

设任意一组数控铣刀参数样本 (xm，ym)，其中xm=[xm1，xm2， …，xm7]T对应该组样本数据中7个铣刀影响参数的输入值，ym代表该组样本数据中刀具寿命期望输出值，由上文可知隐含层的节点数为7，令激励函数为h(x)，该参数样本下模型预测结果可以用式(2)表达.

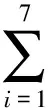
(2)

式中：ai=[ai1，ai2， …，ai7]T，代表模型输入层到第i个隐含层节点的权值；bi表示隐含层第i个节点的阈值，ai·xm表示输出的权值矩阵，ai和bi为系统随机产生；β=[β1，β2， …，β7]T表示连接隐含层与输出层的权值，由于sigmoid函数具有严格递增性，并且能够调节线性与非线性的关系，所以选择sigmoid函数作为激励函数，对式(2)简化可写成为

y*=(HTβ)

(3)

由式(3)表明，若β确定，即可确定ELM模型的唯一性．对于给定的输出样本ym， ELM模型的目标是使模型的预测值与期望值差值最小，用公式表示为

minβ||HTβ-ym||

(4)

对β进行求解可以得到

(5)

2．2基于GA的ELM数控铣刀寿命预测模型优化

在ELM预测模型中，输入层的权值矩阵以及隐含层偏差具有随机性，可能存在部分数值为0的情况，从而造成ELM模型的性能下降． GA作为一种随机并行搜索算法，具有鲁棒性优良、全局索引能力强等优点，尤其针对多峰值的问题拥有极佳的全局把控能力[12]．因此，采用GA对ELM模型中的权值和阈值进行编码，通过输入样本数据完成ELM模型的训练，并将得到的误差经过转换后作为GA的适应度值.基于适应度函数值采用“轮盘赌”算法对种群个体进行选择操作，待操作完成对ELM模型中的权值与阈值进行更新．当算法满足结束条件时，可以获取最佳的权值矩阵及阈值，最后获得一个优化的ELM模型．

2．3预测模型的算法实现

基于GA-ELM算法的设计流程如图2所示．

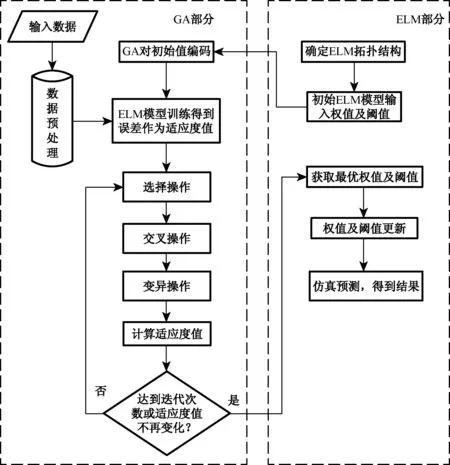
图2 基于GA-ELM算法流程图Fig．2 Algorithm flowchart based on GA-ELM

算法的主要步骤如下：

Step1初始化．随机产生初始种群，其规模(种群个体)S通常设置在30～40区间内，并设置进化次数．在本ELM模型中，网络结构为7-7-1，对ELM模型中的权值及阈值进行编码，计算出染色体长度是7×7+7=56，7×7代表输入层到隐含层之间的权值个数为49，7代表隐含层节点的阈值个数．种群染色体的详细信息如式(6)所示．

(6)

式中：Cγ代表种群中的第γ个个体，满足1≤γ≤S；aij、bi在[-1， 1]区间内随意取值．

Step2样本数据归一化．由于各因素代表的物理含义不同，数量级不一致，为防止对训练结果造成干扰，为此将数据进行归一化操作．其计算如式(7)所示.

(7)

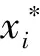
Step3编码方式．由于二进制编码和解码过程繁琐，计算复杂，因此对权值及阈值的编码采用实数编码形式，提高算法的精度与效率．

Step4适应度函数．将适应度函数用来对个体的优劣程度进行评估，在本文中其表达形式如式(8)所示．

(8)

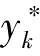
Step5个体选择．对种群个体遍历，依据样本数据及随机产生的权值矩阵及偏差完成适应度函数的计算，然后根据“轮盘赌”算法对个体进行交叉和变异操作．

Step6遗传操作．由Step 5确定父代个体，交叉概率用pc表示，变异概率用pm表示．

(1) 交叉操作．交叉的父代由Step 5产生，采用双亲双子交叉方式，交叉算子的定义如下：

(9)

式中：b为0到1之间的随机数.式(9)表示种群中的第k个染色体ak与第m个染色体am在第j位发生交叉操作．当交叉完毕后对新个体的适应度进行计算并与父代个体进行比较，判断其优劣．

(2) 变异操作．种群中每次应有k×pm个染色体会进行变异操作，随机生成一个[0， 1]内的数对染色体任意位置的基因进行替换，实现对染色体的变异．

经过以上操作，得到新权值与阈值，如果算法达到迭代次数或适应度值经过几代之后不再改变，则算法停止运行，将最终结果代入模型，更新得到铣刀预测模型；否则，转入到Step 5，继续新的交叉及变异操作．

3 实例分析

3．1样本数据获取

本文以文献[9]中的数据作为铣刀寿命预测的样本数据，采用数控铣刀作为试验刀具，刀具材料为YT15硬质合金，待加工工件材料为45号钢，选用粗铣方式加工．

在上述条件下一共获取22组试验数据，将其中前17组数据作为训练集，用来对ELM模型进行模拟训练，将最后5组数据作为预测集，完成寿命预测．刀具寿命预测的样本数据如表2所示．

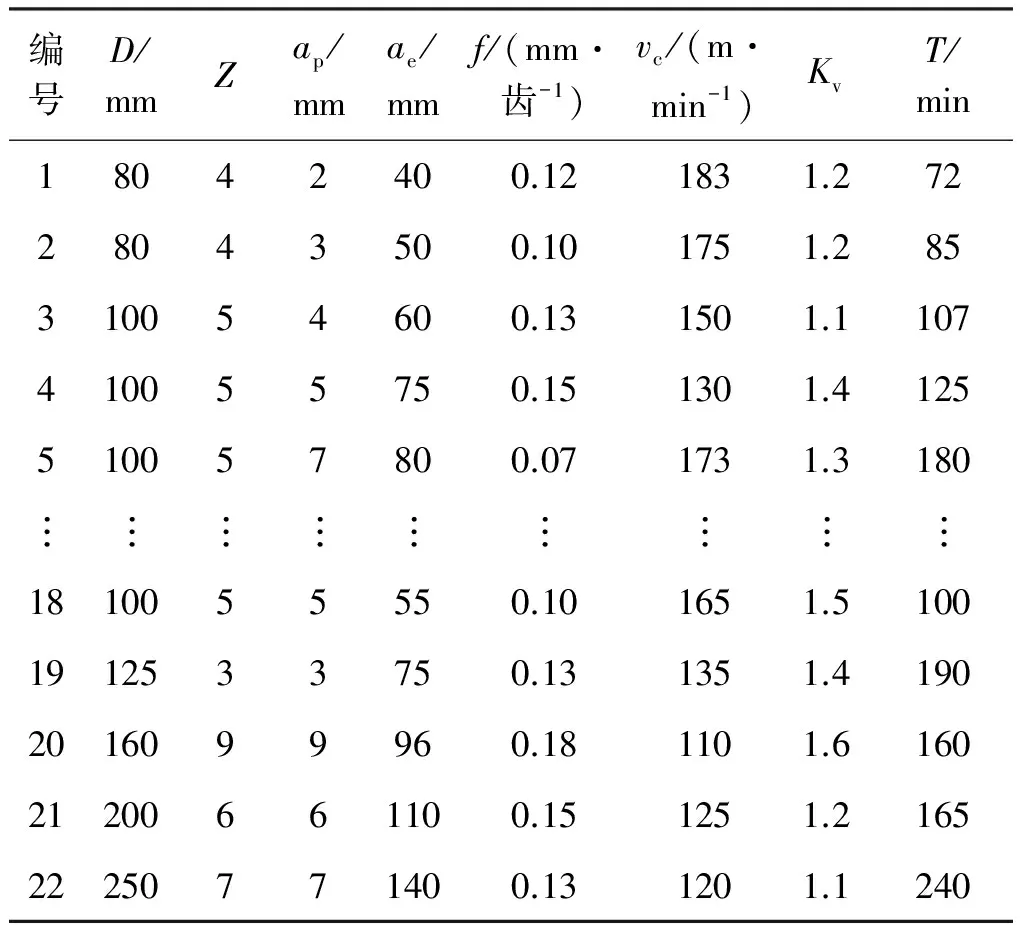
表2 样本数据Table 2 Sample data

3．2结果分析

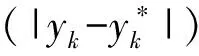
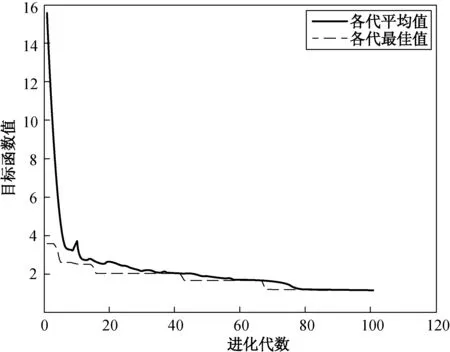
图3 GA-ELM算法目标函数迭代进化过程Fig．3 The objective function iterative evolution process of GA-ELM

输入样本数据，并将GA优化后的输入权值及矩阵代入ELM模型，得到的试验结果如图4所示．由图4可知基于GA-ELM模型的预测结果与真实结果比较接近．

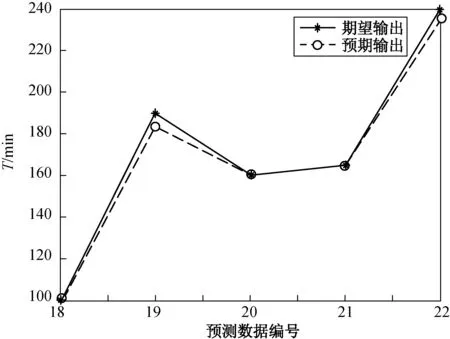
图4 预测样本与真实值比对图Fig．4 Figure of forecast data compared with true value

将预测结果经统计和整理后得到表3所示的数据.

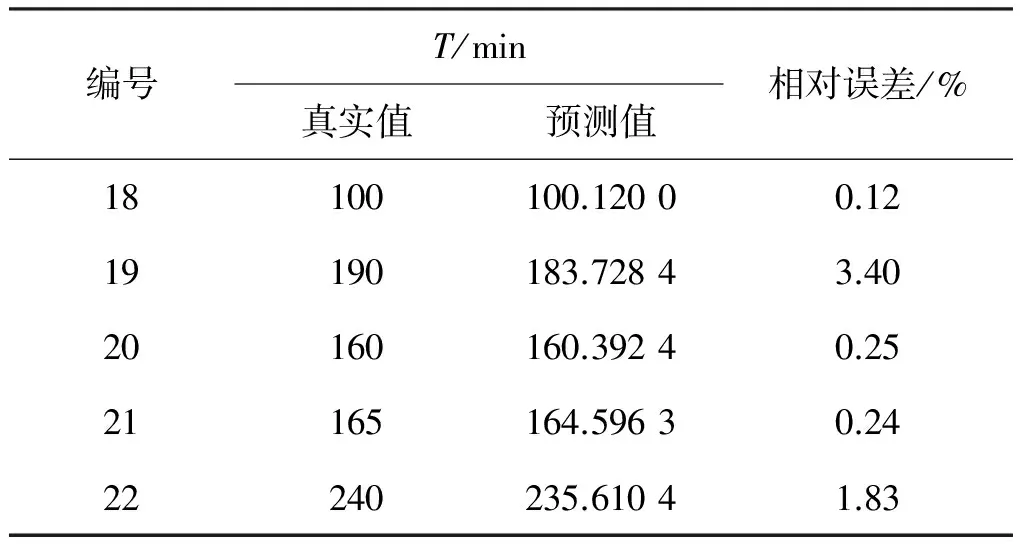
表3 基于GA-ELM模型预测结果分析Table 3 Analysis of model predictions based on GA-ELM

由表3可知，刀具寿命预测结果的相对误差比较小，除编号19外，其余预测刀具寿命相对误差基本都控制在2%以内，由此可表明GA-ELM模型在刀具寿命预测上取得了良好的效果．

3．3模型对比

本文数据样本来源于文献[9]，为了验证GA-ELM模型对刀具寿命预测的优越性，与文献[9]中的试验结果进行综合比对，该文献中应用3种算法对刀具寿命进行预测，分别为基本BP算法、优化后的BP算法以及基于粒子群优化的BP算法．文献[9]研究表明：基本BP算法得到的刀具寿命相对误差值高达17．37%，并且测试样本的相对误差均值要远远大于训练样本的相对误差均值，进而验证了基本BP算法泛化能力比较差；通过权值优化的BP模型得到的刀具寿命相对误差为12.00%，较基本BP算法有了一定提高，但是泛化能力依旧没有改善；基于粒子群优化的算法较上述两种算法有了明显的提升，刀具寿命相对误差为6.00%左右，并且泛化能力有了很大改善．本文采用基于GA-ELM算法模型得到的刀具寿命最大相对误差仅为3．4%，且泛化能力强，收敛性好．

4 结 语

本文基于GA改进ELM模型，通过GA对输入权值及阈值进行优化，获得性能最佳的参数来确定出最终的ELM预测模型．将本文的算法模型与文献[9]中应用的算法进行对比，表明本文采用的基于GA-ELM的算法模型具有更好的准确率和泛化能力，在铣刀寿命预测中具有明显的优势．

[1] 张锴锋，袁惠群，聂鹏．基于切削声信号与优化SVM的刀具磨损状态监测[J]．振动测试与诊断，2015，35(4)：727-732．

[2] 柳洋，陈永洁，杨文恺，等．刀具磨损在线监测研究现状与发展[J]．机床与液压，2014，42(19)：174-180．

[3] ZHANG Z， LI L， ZHAO W． Tool life prediction model based on GA-BP neural network[J]． Material Science Forum，2016，836/837：256-262．

[4] 丁怡，何卫平，张维，等．基于BP神经网络的刀具寿命预测模型[J]．航空制造技术，2010(8)：93-96．

[5] 侍红岩，吴晓强，张春友．基于支持向量回归机的刀具寿命预测[J]．工具技术，2015，49(11)：47-50．

[6] 卫敏，余乐安．具有最优学习率的RBF神经网络及其应用[J]．管理科学学报，2012，15(4)：50-57．

[7] HUANG G B，ZHU Q Y，SIEW C K．Real-time learning capability of neural networks[J]． IEEE-Transaction on Neural Networks，2006，17(4)：863-878.

[8] HUANG G B，ZHU Q Y，SIEW C K．Extreme learning machine： Theory and applications[J]． Neurocom-puting， 2006，70(1/2/3)：489-501.

[9] 薛宏．企业级刀具全生命周期管理系统研发[D]．重庆：重庆大学机械工程学院，2015．

[10] 刘芳文．影响刀具耐用度的因素[J]．现代技能开发，2001(10)：53．[11] 杨建国，熊经纬，徐兰，等．基于改进极限学习机的纱线质量预测[J]．东华大学学报(自然科学版)，2015，41(4)：494-497．

[12] 王银年．遗传算法的研究与应用[D]．无锡：江南大学机械工程学院，2009．

(责任编辑：徐惠华)

StudyonPredictionModelofCNCMillingCutterLifeBasedonGA-ELM

ZHOUYaqin，YANGJianguo，LIUKaiqiang，YOUXiang

(College of Mechanical Engineering， Donghua University， Shanghai 201620， China)

In the process of machining， the wear condition of the tool has an important effect on the machining quality of the parts． Accurately predicting the tool life is one of the key functions that the intelligent manufacturing system must have． Based on the analysis of the influence factors of the life of CNC (computer numerical control) milling cutter， the extreme learning machine (ELM) algorithm model is introduced to establish the life prediction model of CNC milling cutter． In the process of life prediction， the input weight and hidden layer threshold of ELM model are optimized by genetic algorithm (GA)， and the life prediction model of CNC milling cutter based on GA-ELM is established． The prediction results are compared and analyzed with basic BP neural network， BP neural network， based on particle swarm optimization BP neural network, the results show that the tool life prediction model based on GA-ELM is superior to the other three algorithms， which is an effective and accurate tool life prediction algorithm．

tool life； genetic algorithm (GA)； extreme learning machine (ELM)

K 826．16

A

1671-0444 (2017)04-0515-05

2017-04-05

上海市自然科学基金资助项目(15ZR1400600)；上海仓储物流设备工程技术研究中心资助项目(17DZ2283800)

周亚勤(1977—)，女,江苏盐城人，副教授，博士，研究方向为智能生产调度.E-mail：zhouyaqin@dhu.edu.cn