ARIMA模型在LMT数据处理中的应用

邓方进， 王绪本， 李德伟

(成都理工大学 地球物理学院,成都 610059)

ARIMA模型在LMT数据处理中的应用

邓方进， 王绪本， 李德伟

(成都理工大学 地球物理学院,成都 610059)

为了解决LMT时间序列出现的缺失和强干扰现象，根据实测资料数据量大、非线性、非平稳性等特点，首次采用ARIMA模型进行预测和填补，基于平稳性检验和贝叶斯信息准则确定模型阶数，采用最小二乘原理确定模型参数，建立双向预测模型和线性合并方法进行预测，并对比ARIMA模型和AR模型预测数据的准确度。实例表明，ARIMA模型预测结果准确，精度比AR模型高，且误差不会累积，解决了原始资料的不连续性和强干扰的问题。

ARIMA模型; 预测; 大地电磁测深; 资料处理; 缺失数据

0 引言

在大地电磁测深(Magnetotelluric，MT)资料处理过程中，为了得到研究区域合理的地电属性特征，就必须保证有较高质量的野外原始观测数据。方胜[1]总结了在大地电磁野外数据采集过程中，如何保证数据质量的操作经验。但是实际的长周期大地电磁测深(Long period Magnetotelluric，LMT)的数据测量位置选在远离城区电磁干扰较小的平坦地区，测量周期长达半个月甚至数个月，在LMT仪器的运行过程中，由于仪器的响应问题，采集到的电磁场时间序列偶尔会出现部分缺失和随机强干扰现象。数据的缺失对长周期资料处理影响非常大，长周期数据地处理需要半个月甚至几个月的数据进行分析和处理，并且时间序列是需要连续不间断的。为了保证大地电磁测深资料的准确度，就需要选择一个适当的方法对缺失数据进行填补。

Box&Jenkins[2]提出著名的差分自回归滑动平均模型(Autoregressive Integrated Moving Average Model, ARIMA)时间序列预测方法，能够准确地预测非平稳时间序列，只需要给出时间序列的前N个连续数据，就可以采用该预测模型进行数据的预测，并针对澳大利亚1972年到1991年的居民消费价格指数(Consumer Price Index，CPI)，根据自相关函数和偏自相关函数的性质确定模型阶数建立ARIMA模型，预测未来四年的CPI数值；许立平等[3]根据1973年1月至2010年11月伦敦黄金月度价格建立ARIMA模型，预测2011上半年的黄金价格走势，并得出短期上涨的结论；张勃等[4]将ARIMA模型用于生态足迹动态模拟和预测。关于ARIMA模型在地球物理领域的应用，唐恒专[5]应用AR模型对地震信号P波初至时段及其后一时段进行建模，求出预测误差并将其作为特征判据对地震信号进行分类和识别。

1 MT数据缺失和强干扰现象

MT资料处理的目的是从采集到的大地电磁时间序列中，提取出能够反映研究区域的地电特性的各种频率成分，通过计算得到准确的阻抗张量要素、视电阻率、相位以及其他相关的大地电磁响应函数，从而获得研究区域的电性结构，为资料解释提供依据[6]。目前，大地电磁测深数据处理方法有远参考法[7]、Robust法[8]、Hilbert-Huang变换法[9]、S变换[10]等。常使用的方法是采用傅里叶变换将大地电磁场的时间序列向频率域转换，这些处理方法都是针对原始资料的时间序列是连续的。

LMT数据采集仪器将采集到的数据保存到TF存储卡里，存储卡中的数据包含了表征地电结构的原始数据和其他干扰数据，其中干扰数据来源于外界影响和内部影响，其中外界影响包含了人为电磁场干扰和自然电磁场干扰，如高压输电线、工厂、磁暴和雷电等；内部影响由于仪器内部元件的影响，如电极、磁棒和仪器主机的故障。在资料整理过程中，需要尽量剔除噪声干扰数据，常用平滑滤波的方法筛选出质量较高的数据，将挑选出来的数据再进行下一步处理。但是实际的野外工作中，随机干扰数据可能会导致原始资料在某一段时间内出现电磁场数值特别大或者特别小的情况。对于这种情况，采用滤波方法进行消除就会对资料的有效信号产生影响，所以可以采用一种合理的方法将随机干扰数据进行置换。

为了得到低频段的资料，要尽可能减小截断效应，增大记录长度，保证低频段也有足够多的叠加次数，由于探测深度的不同，长周期大地电磁信号对应的周期范围在10 s～20 000 s，通常要保证记录长度不低于最低频率所对应周期的6倍，则需要在测点上采集足够长的时间。经过长期的野外测量工作，特别是针对采集时间长达半个月甚至数个月的LMT探测会出现这样的问题：在野外的数据采集过程中，LMT测量仪器会偶尔出现故障，仪器工作不稳定的状况，这种偶然情况就会导致记录到的电磁场数据出现缺失，缺失数据1个～30个不等。在进行资料处理时，对于这种原始资料缺失情况导致时间序列不连续，可能会造成在记录状态下的高质量数据无法利用。因此，找到一种合理的预测模型对有缺失的LMT数据进行填补，弥补由于仪器硬件原因造成的不足，可以提高LMT资料的利用率。

对LMT数据的分析及处理，张伟[11]在信号去噪和时频分析等方面做了很多研究，张春虹等[12]将无激励的AR预测模型用于预测大地电磁测深缺失数据，但是存在预测精度和预测个数的不足。

2 大地电磁场信号特征分析

2.1 信号的分类

在实际信号的过程中，尽管信号的处理方法和基本原理都相同，但是针对不同学科领域的不同信号或者同一学科的不同信号，处理过程也会存在很多差异。所以在做信号处理之前，首先要明确信号的类别，现代信号处理中对信号的特征将信号分为以下几类[13]：

1)线性信号和非线性信号。线性信号就是基于线性系统的信号，该系统具有齐次性和可加性两个性质；而非线性信号不满足上述线性系统的性质。

2)平稳信号和非平稳信号。平稳信号满足平稳性特征，最大特点是它的统计特征与时间分布无关。其特征为：①序列均值为常数; ②序列二阶矩有界; ③序列协方差函数与时间无关，只与时间间隔有关; ④序列联合概率分布函数与时间无关，只与时间间隔有关。不满足以上特征的信号为非平稳信号。

3)高斯信号和非高斯信号。高斯信号定义为概率密度分布为正态分布的随机信号。在随机过程中使用偏斜度和峭度两个常量来描述该随机过程，高斯信号的偏斜度和峭度都为零，而不满足该类条件的随机信号都为非高斯信号。

通过对信号进行分类，确定信号的类型，在处理数据时，根据信号特征选择合适处理的方法，才能“对症下药”，准确地对信号进行处理，得到合理的处理结果。

2.2 实测大地电磁信号特征分析

大地电磁场是指地球天然电磁场中随时间变化的电场和磁场，频率范围宽。它们是由太阳不断射出的粒子流与电磁辐射在地球周围空间所引起的电磁效应所形成的。通过采集天然变化的电磁场分量，将电磁场信号转换成视电阻率曲线和相位曲线，反演求得各地层的电阻率和厚度值。

20世纪中期，进行大地电磁数据处理前，通常假设天然场的大地电磁信号是具有线性、因果性、平稳性和最小相位性等特征的随机信号，并且统计特征满足高斯分布。21世纪初期，随着现代信号处理方法的发展，对信号特征的分析研究取得了新的进展，大地电磁信号的研究思路也发生了重大转变。王书明等[14]根据大量实测资料进行分析研究，其结果表明大地电磁信号的零极点图不满足最小相位系统的要求；分析实测资料的高阶统计量，证明了大地电磁信号是非高斯性，通过相关系数证明信号是非平稳的，并且不满足线性要求。

LMT野外资料采集时间长，本次试验采样频率为1 Hz，以200 h的观测时长进行计算，那么采集的电磁场一个分量数据达到了720 000个，电磁场包含了电磁的5个分量，那么五道数据就共计3 600 000个，数据文件大小近百兆。

图1为陕西某地LMT采集资料中某一天的记录数据，使用LEMI-417仪器，采样率为1 Hz，采集大地电磁场五分量数据，包含两个电场分量Ex和Ey，三个磁场分量Hx、Hy和Hz。

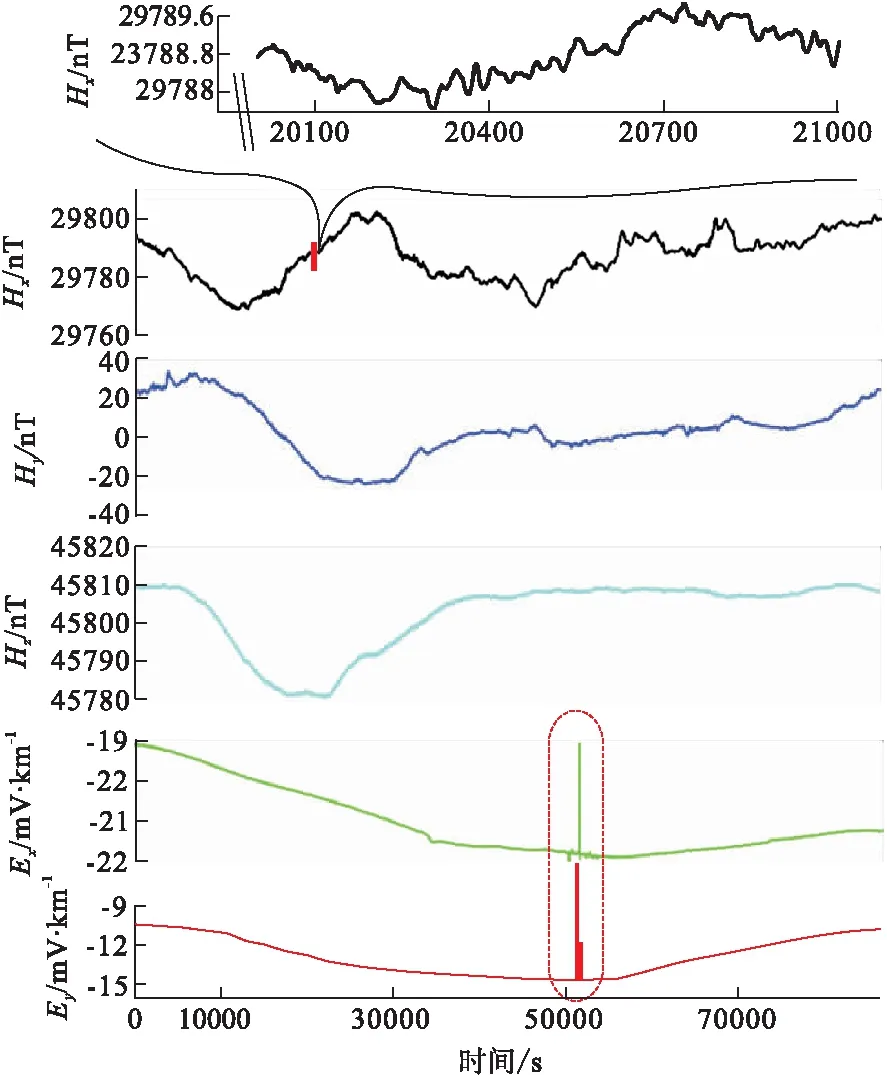
图1 陕西某地实测一天的LMT数据曲线图Fig.1 Graph of LMT data in Shanxi province

由图1可以看出，每一条曲线图没有一个明确的趋势，很难用一个确切的函数来表达。整个时间序列中，每一道数据的振幅的幅值极值相差不大，变化较小，相对来说，磁场的变化比电场的变化大，电场的曲线趋势相对平稳。但是在其中50 000～55 000数据区间中，见红色虚框内，电场两个方向的都出现了一个明显的跳动(这是偶然现象，出现次数不多)，出现跳动的时间点一致，证明这些时间点的数据存在信号干扰。将Hx道中数据中20 000～210 000中的1 000个数据(约17 min)提出来另成图像，可以看出，在相对上升趋势的曲线中，也存在诸多类似正余弦信号的叠加信号。

随着时间序列非平稳性的提出，单位根检验目前已经成为宏观数据建模前首先要进行的工作。为此，Dickey等[15]提出了著名的单位根检验方法(Augmented Dickey-Fuller test， ADF检验)，用于检验序列的平稳性。

ADF检验是通过下面三个模型完成的：

模型1：

(1)

模型2：

(2)

模型3：

(3)

式中：t为时间变量；α为常数项；βt为趋势项；εt为残差Xt项；Xt为原始序列；为ΔXt差分序列。原假设H0:δ=0，检验时从模型3开始，然后模型2，最后模型1，若检验拒绝H0:δ=0，则原始时间序列不存在单位根，即序列为平稳序列，即可停止，若检验接受H0:δ=0，则序列为非平稳序列。通过对大地电磁场的电磁数据进行平稳性分析，检验结果为非平稳。

长周期大地电磁仪所采集的五分量大地电磁场时域数据，属于时间连续的随机非周期信号，并且具有非线性、非高斯性、非最小相位性等特点。野外测量时间长，在时域表现出数据量庞大和非平稳性的特征，这些特征为后续信号处理方法的选择提供了依据。

3 ARIMA模型及其预测方法

3.1 ARIMA预测模型

ARIMA 模型的基本原理：把时间序列视为随机过程，用一个数学模型来描述或模拟；可用该时间序列的过去值和现值来预测未来值。该模型考察了时间序列的动态、持续特征，揭示了时间序列过去与现在、将来与现在的相互关系。

若序列{X}能通过d次差分后变成平稳序列{Y}，则：

yt=Δdxt

(4)

那么可以建立模型

(5)

(6)

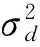
3.2 ARIMA模型阶数的确定及参数估计

对于非平稳序列，相应的措施是进行差分处理使其平稳。在连续变化的时间范围内，变量X关于时间t的变化率用dX/dt来表示；对于离散的变量{X}，我们常取在规定的时间区间上的差商ΔX/Δt来表示变量的变化率，如果选择Δt=1，则

ΔXt=Xt-Xt-1

(7)

其中：时间t取非负数；ΔXt则为差分序列。对差分序列再进行ADF检验，若检验结果还是非平稳，则继续进行差分处理，直到检验结果为平稳。期间所进行的差分次数则为ARIMA模型的差分阶数d。

确定了差分次数，接下来确定阶数p(AR模型的阶数)和q(MA模型的阶数)。常用的定阶方法：最终预测误差[16]、阿凯克信息准则(Akaike information criterion，AIC)[17]、BIC[18]以及奇异值分解[19]等。

AIC准则法的原理是使得式(8)最小。

(8)

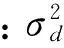
笔者采用贝叶斯信息准则法(Bayesian Information Criterion，BIC)，是一种改进的AIC准则法。原理是使得式(9)为最小，BIC的准则比AIC更严格。

(9)

根据经验法[20]，当N=20～50时，AR模型最大阶数定为N/2,当N=50～100时，最大阶数选在N/3～N/2,当N=100～200时，最大阶数定在2N/ln(2N)效果会相对比本文好，所以在进行模型定阶时，可以依据经验法缩小阶数确定范围。

模型参数的精细估计采用最小二乘准则来进行，并有近似极大似然估计等估计方法。

3.3 双向预测和线性合并

通过对比大量的预测数据与真实数据，发现随着时间地增长，其预测误差会越来越大。结合LMT缺失数据的特性，数据的缺失部分不会出现在数据的开头和结尾部分，那么就可以结合从前往后的预测结果和从后往前的预测结果综合决定最后的结果。具体方法是首先从缺失数据前的N个数据预测k个数据，采用ARIMA模型的预测结果为ans1(k)，然后从缺失数据后的N个数据反向预测k个数据，预测结果为ans2(k)，设计线性比例a(k)和b(k)：

(10)

与

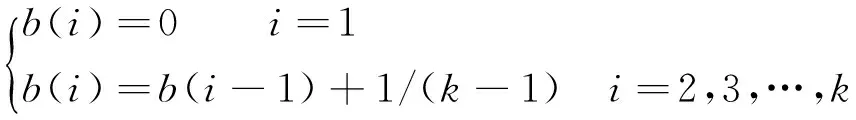
(11)

通过线性比例，将两次前后分别进行的预测值进行合并，最后的合成结果为ans(k)：

ans(i)=a(i)*ans1(i)+b(i)*ans2(i)

i=1,2,…,k

(12)

将此序列作为最终的预测结果，因此随着预测个数的增加，预测值和实测值误差不会累积，理论上预测数据的开头和结尾部分误差相对较小。

3.4 ARIMA模型预测步骤

采用ARIMA预测模型对含有缺失数据的序列进行预测，对需要置换的数据进行修补，程序流程如图2所示。

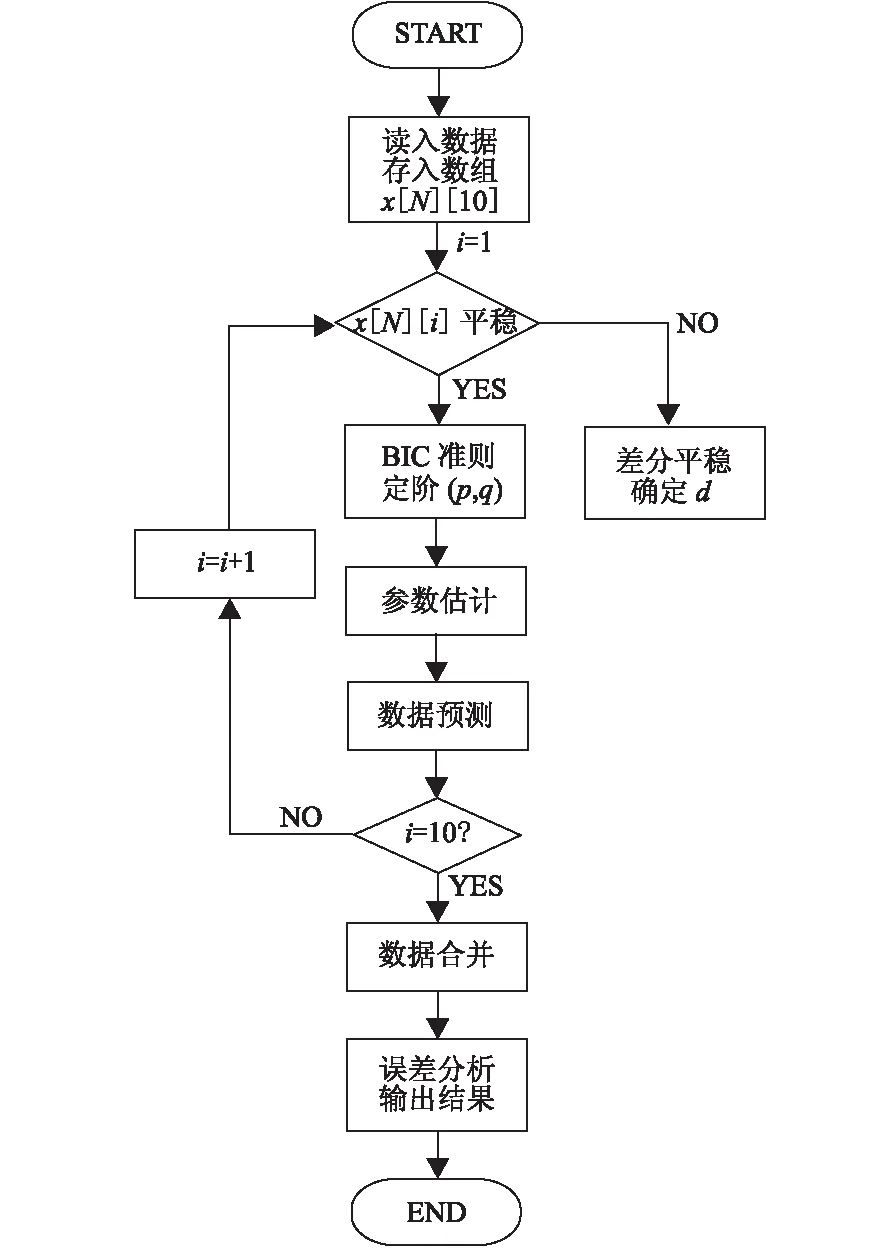
图2 ARIMA模型数据预测流程图Fig.2 The flow chart of predict data using ARIMA model

1)输入需要进行预测的大地电磁序列，确定序列个数N，预测数据个数k，提取预测区间前N列和后N列，分离有用数据存入二维数组x[N][10]。

2)将预测区间后N列数据进行反向处理，然后对每列数据进行平稳性检验，如果检验结果非平稳，则进行差分处理，直到序列平稳。

3)通过BIC准则确定模型阶数，采用最小二乘方法进行参数估计，再进行参数估计及数据预测，并通过双向预测进行数据合并。

4)进行预测数据与真实数据的误差分析，并输出结果。

4 ARIMA预测模型应用实例

4.1 大地电磁缺失数据的预测

以LEMI-417长周期大地电磁仪所采集的五分量大地电磁场数据为例，利用ARIMA模型分别对LMT资料的时间序列中磁场x分量(Hx)、磁场y分量(Hy)、磁场z分量(Hz)、电场x分量(Ex)和电场y分量(Ey)中缺失的时域数据进行预测，笔者以采样率为1 s的LMT时域序列作为实验样本数据，随机取430个约4 min的数据作为分析模型(图3)。

图3中包含了电磁场五个分量的曲线图，每个分量的形态不一，有相对平稳序列如Ex；非平稳序列，如Hz存在下降趋势；数据波动较大的曲线如Ey。图3中红色虚线内的数据(200-230)作为本次试验的预测目标数据，ARIMA预测模型所使用到的数据包含预测区间前200个数据和预测区间后200个数据。

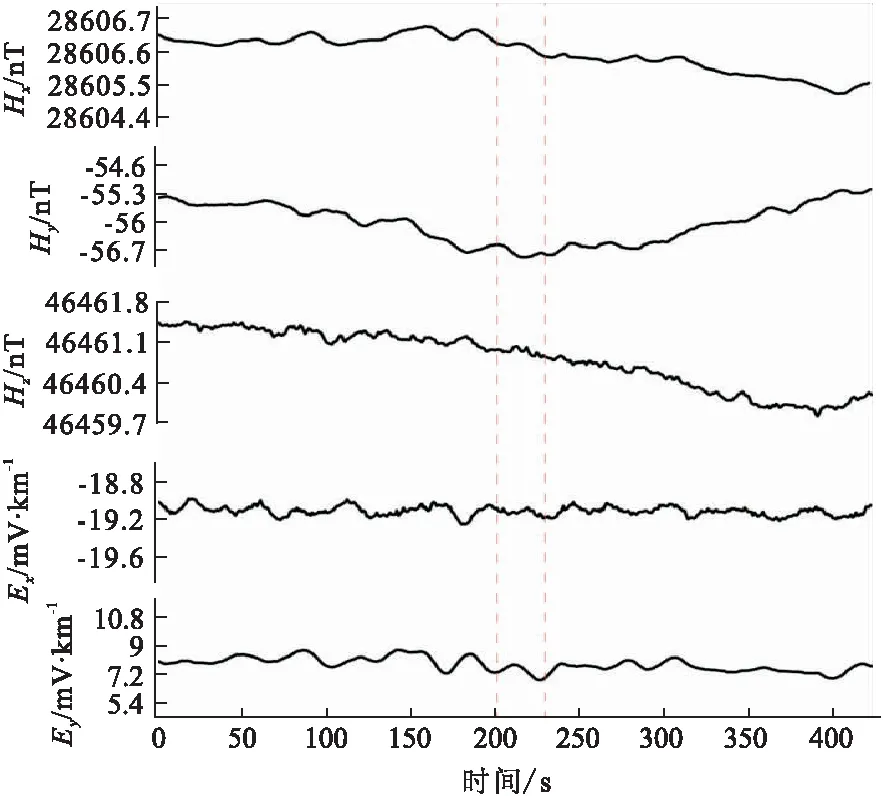
图3 原始LMT时间序列曲线图Fig.3 Time series graph of raw LMT data

4.2 预测结果分析

通过ARIMA模型对时间序列缺失的30个数据进行预测填补后，将预测结果与实测数据进行对比，为了直观反映预测结果与实测数据进行对比，图4给出了ARIMA模型预测后的各分量的缺失数据和实际样本数据的散点图比较。

图4 预测数据和实测数据误差对比图Fig.4 The comparison of predicted data and observed data

由图4可以看出，ARIMA预测的数据和实测数据基本重合，其曲线走向基本一致。AR模型预测的数据当曲线走势较为平稳时，其效果较好，但是当曲线有明显的上升或者下降的趋势时(如Ey)，其预测结果前5个的准确度较高，而其后面的数据误差则越来越大，这是因为误差累积造成的。所以ARIMA模型预测的结果准确度比采用AR模型预测的结果高，随着预测个数的增加，预测数据值和真实值的误差并没有像常规预测方法那样会出现误差的累积而造成误差逐渐增大。对于数据本身波动较大的情况，预测误差相对较大。

表1为ARIMA模型预测数据与真实数据的误差值，表1中ΔHx、ΔHy和ΔHz分别表示磁场的x分量、y分量和z分量预测值和真实值的误差绝对值，ΔEx和ΔEy分别表示电场x分量和y分量预测值和真实值的误差绝对值。

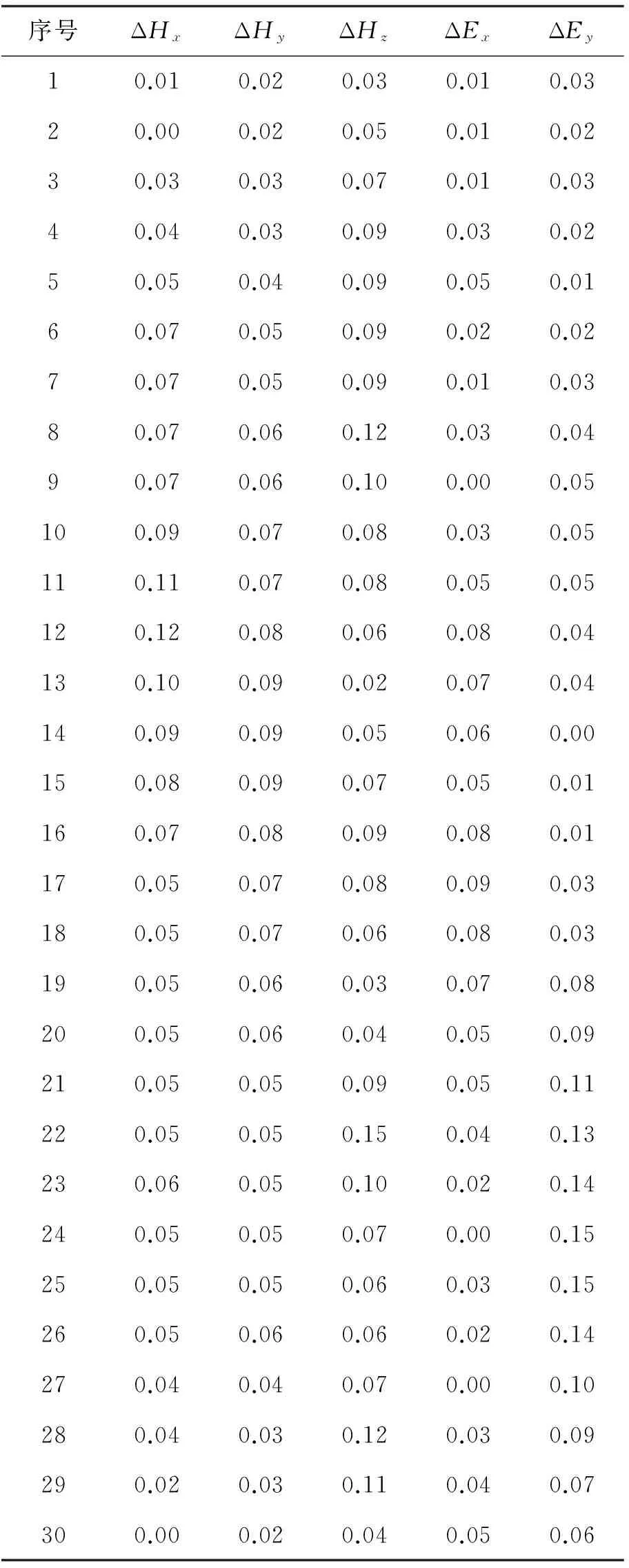
表1 预测数据与实测数据误差表

从表1中可以看出各个分量的整体误差值都比较小，通过计算平均误差为0.06，可以满足作为资料处理的要求。

为了直观地表示ARIMA预测模型和AR预测模型预测数据与实测数据的误差对比，对两者的误差数据绘制误差散点图，如图5所示。

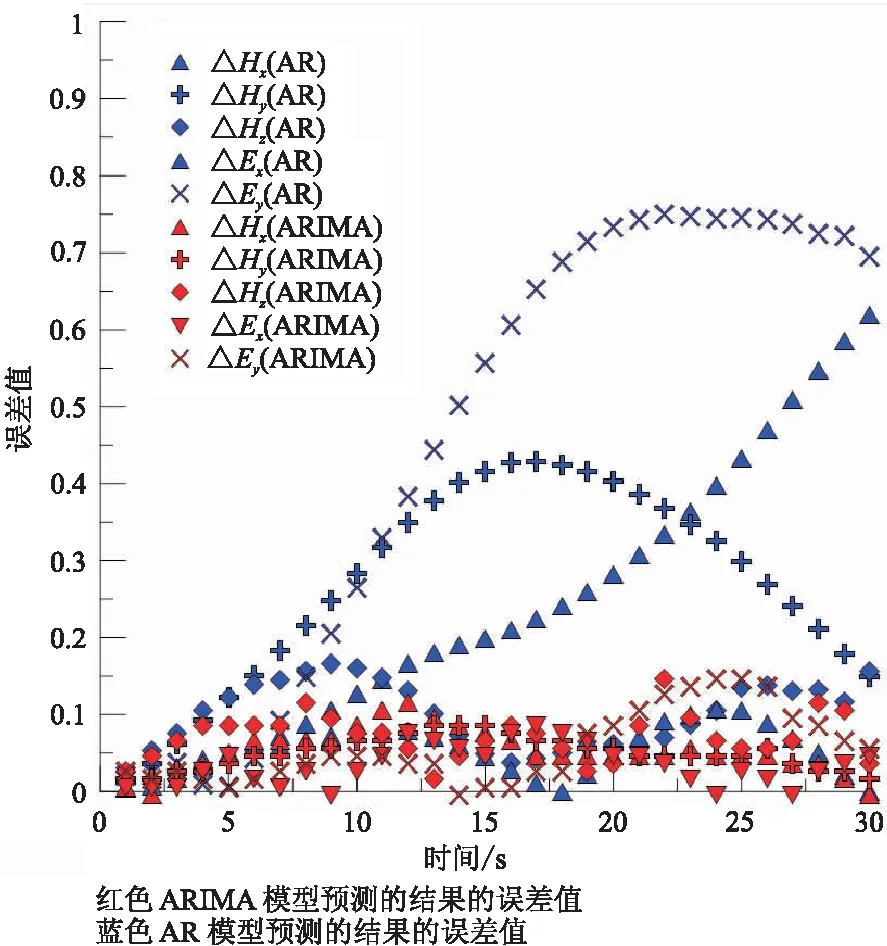
图5 预测数据与实测数据误差散点图Fig.5 Error scatterplot of predicted data and observed data

由图5可以看出，ARIMA模型预测数据的误差绝对值都保持在0.2以下，并且误差值不会随着预测个数的增加而增加。而采用AR模型预测的结果的误差总体偏大，最大可达到0.8，由于误差累积，随着预测个数的增加，整体呈现上升的趋势。通过图5的对比可知，采用ARIMA预测模型预测的结果误差值比AR预测模型的结果误差值小，且误差相对稳定。所以采用ARIMA预测模型对LMT缺失的30个数据进行预测填补的方法是可行，且结果较好。

为了进一步验证ARIMA模型预测数据的准确定，反映经过ARIMA模型对缺失数据进行填补后的数据在大地电磁测深资料处理中的影响，分别对实测原始数据和经过ARIMA模型预测填补后的数据进行频谱分析。原始数据前后平均选取共计2 048(211)个数据，预测数据根据原始数据选取的原则在相同位置选取相同个数的数据，进行傅里叶变换，将时域数据变换到频率域，则得到预测填补后的数据与实测数据的频谱对比(图6)。

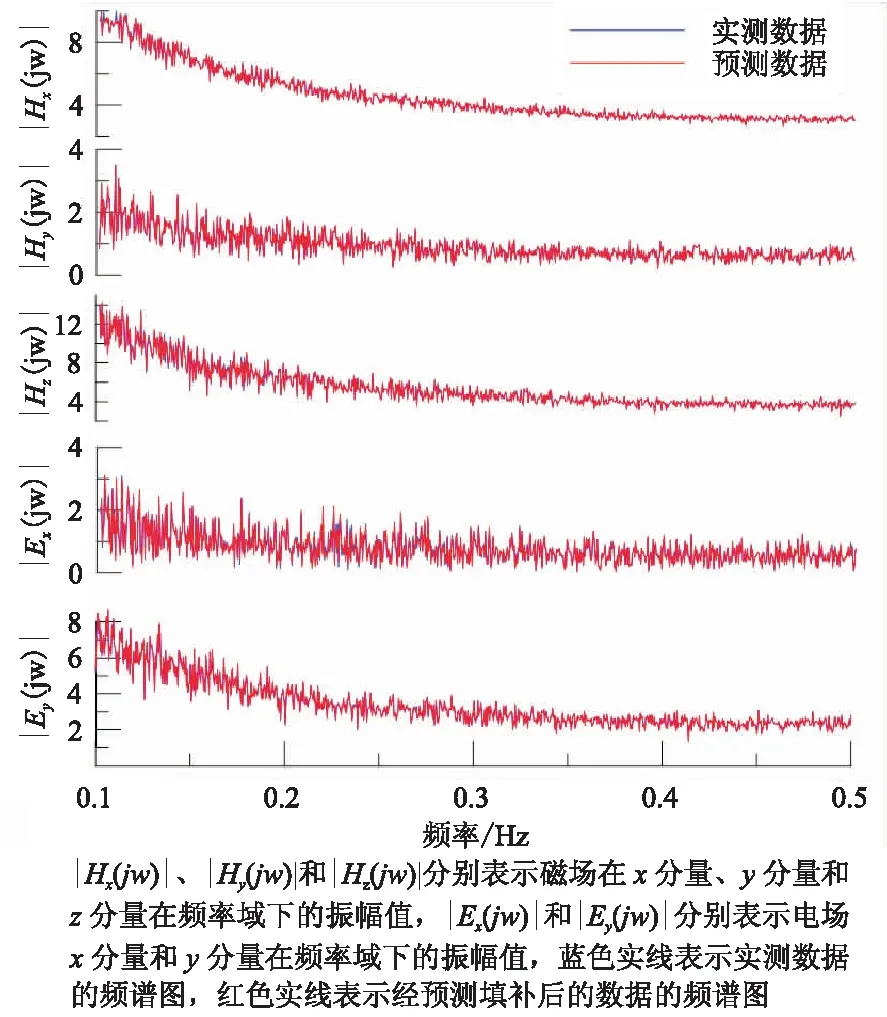
图6 预测填补后的数据与实测数据频谱对比Fig.6 Comparision of the spectrum of observed data and the predicted data

由图6可以看出，红色实线和蓝色实线基本重合，表明经ARIMA模型预测填补后的数据频谱与原始数据的频谱差值很小，基本可以忽略，故经预测填补后的数据对整体数据频谱基本不会产生影响。所以采用ARIMA模型与缺失数据进行预测和填补是可行的。对于强干扰数据(如图1中的电场跳点)，就可以直接将干扰数据定义为缺失数据进行处理，采用预测数据进行置换，但是当野外采集到的数据出现长时间的数据缺失现象或者干扰数据较多时，就需要重新对数据进行采集，以便得到更加准确的原始数据。

5 结论

笔者将ARIMA预测模型应用到LMT缺失数据的填补中，可以较好地还原野外数据采集过程中缺失的数据。实验结果表明，ARIMA预测模型预测结果精度比AR模型高，随着预测个数的增加，预测误差值不会逐渐累加而增大，而是保持在一定范围之内。ARIMA预测模型对原始LMT数据进行预处理，可以得到完整的野外观测资料，置换由于强干扰导致数据出现的跳点，满足大地电磁资料处理过程中对数据完整性的要求，提高了野外采集数据的利用率。因ARIMA预测模型对于缺失数据个数较多的数据其预测结果误差较大，对于出现长时间的数据缺失或者干扰数据较多时，建议对该测点进行从新测量，以获得更准确的原始资料。

[1] 方胜.如何保证大地电磁测深原始资料的质量[J].地球科学,1990(S1):14+80.

FANG S. The way to guarantee the quality of magnetotelluric sounding raw data[J]. Earth Science,1990(S1):14+80.(In Chinese)

[2] BOX G E P,JENKINS G.Time series analysis forecasting and control[J].Journal of the Operational Research Society,1976,22(2):199-201.

[3] 许立平,罗明志.基于ARIMA模型的黄金价格短期分析预测[J].财经科学, 2011(1):26-34.

XU L P, LUO M Z. Short-term analysis and prediction of gold price based on ARIMA model[J].Finance&Economics, 2011(1):26-34. (In Chinese)

[4] 张勃,刘秀丽.基于ARIMA模型的生态足迹动态模拟和预测——以甘肃省为例[J].生态学报,2011,31(20):6251-6260.

ZHANG B, LIU X L. Dynamic ecological footprint simulation and prediction based on ARIMA model: a case study of Gansu province, China[J]. Acta Ecologica Sinica, 2011,31(20):6251-6260. (In Chinese)

[5] 唐恒专.AR模型预测误差比在地震事件识别中的应用[J].数据采集与处理,2004,19(4):446-449.

TANG H Z. Predication error ratio of AR model and its application to seismic event discrimination[J]. Journal of Data Acquisition & Processing,2004,19(4):446-449. (In Chinese)

[6] TRAVASSOS J M,BEAMISH D.Magnetotelluric data processing—a case study[J].Geophysical Journal International,1988, 93(2):377-391.

[7] 田绍耕.远参考法大地电磁测深[J].石油地球物理勘探,1983,18(3):232-235.

TIAN S G. Magnetotelluric using remote reference method[J]. Oil Geophysical Prospecting, 1983,18(3):232-235. (In Chinese)

[8] SUTARNO D, VOZOFF K. Robust M-estimation of magnetotelluric impedance tensors[J]. Exploration Geophysics, 1989, 20(20):383-398.

[9] 汤井田,化希瑞,曹哲民,等.Hilbert-Huang变换与大地电磁噪声压制[J].地球物理学报,2008,51(2):603-610.

TANG J T,HUA X R,GAO Z M,et al.Hilbert-Huang transformation and noise suppression of magnetotelluric sounding data[J].Chinese J.Geophys,2008,51(2):603-610. (In Chinese)

[10] 景建恩,魏文博,陈海燕,等.基于广义S变换的大地电磁测深数据处理[J].地球物理学报,2012,55(12):4015-4022.

JING J E, WEI W B, CHEN H Y, et al. Magnetotelluric sounding data processing based on generalized S transformation[J]. Chinese J. Geophys,2012,55(12):4015-4022. (In Chinese)

[11] 张伟.长周期大地电磁法信号处理关键技术研究与应用[D].成都:成都理工大学,2011.

ZHANG W. Research and application in key single processing technology of Long-period Magnetotelluric[D]. Chengdu:Chengdu university of technology,2011. (In Chinese)

[12] 张春虹,张刚.AR模型在大地电磁测深资料处理中的应用[J].地球物理学进展,2013,28(3):1227-1233.

ZHANG C H, ZHANG G. The application of AR model in magnetotelluric data processing[J]. Progress in Geophys., 2013,28(3):1227-1233. (In Chinese)

[13] 张贤达. 现代信号处理:第二版[M]. 北京:清华大学出版社, 2002.

ZHANG X D. Modern signal processing: second edition [M]. Bejing: Tsinghua University Press,2002. (In Chinese)

[14] 王书明, 王家映. 大地电磁信号统计特征分析[J]. 地震学报, 2004, 26(6):669-674.

WANG S M, WANG J Y. Analysis on statistic characteristics of magnetotelluric signal[J]. Acta Seismologica Sinica, 2004, 26(6):669-674. (In Chinese)

[15] DICKEY D A, FULLER W A. Distribution of the estimators for autoregressive time series with a unit root[J]. Journal of the American Statistical Association, 1979, 74(366a):427-431.

[16] AKAIKE H. A new look at the statistical model identification[J]. Automatic Control IEEE Transactions on, 1974, 19(6):716-723.

[17] AKAIKE H. Fitting autoregressive models for prediction[J]. Annals of the Institute of Statistical Mathematics, 1969, 21(1):243-247.

[18] SCHWARZ G. Estimating the dimension of a model[J]. Annals of Statistics, 1978, 6(2):15-18.

[19] KANJILAL P P, PALIT S, SAHA G. Fetal ECG extraction from single-channel maternal ECG using singular value decomposition[J]. IEEE transactions on bio-medical engineering, 1997, 44(1):51-9.

[20] 何正嘉,訾艳阳,张西宁.现代信号处理及工程应用[M].西安:西安交通大学出版社,2007.

HE Z J, ZI Y Y, ZHANG X N. Modern signal processing and application in engineering[M]. Xian: Xi'an Jiaotong University Press,2007. (In Chinese)

TheapplicationofARIMAmodelinLMTdataprocessing

DENG Fangjin, WANG Xuben, LI Dewei

(Chengdu University of Technology,Chengdu 610059， China)

To solve the deletion or skipping of LMT time series which is is large, nonlinear, non-stationary based on observed data, the ARIMA method is applied to predict the missing data and replace the jump-point. The model order number is obtained through the stationarity test and the bayesian information criteria(BIC), the model parameters is determined using the LS theory. Establishing the bi-directional prediction model and linear combination method to forecast the missing data, then compare the predicted data accuracy of ARMA and AR. The result shows that the ARMA method with higher accuracy and without error accumulation, can solve the problem that the observed data is discontinuity and strong interference.

ARIMA model; predict; magnetotelluric; data processing; missing data

P 631.2

A

10.3969/j.issn.1001-1749.2017.05.05

2017-02-17 改回日期： 2017-03-31

“深地资源勘查开采”重点专项(2106YEC0600302);国家高技术研究发计划(2014AA06A612)

邓方进(1992-)，男，硕士，研究方向为固体地球物理学，E-mail：fangjindeng@126.com 。

1001-1749(2017)05-0612-09