重力场欧拉反褶积最优解提取

周 勇， 曹书锦， 侯萍萍， 杨子龙

(1. 湖南文理学院 资源环境与旅游学院，常德 415000；2. 湖南科技大学 页岩气资源利用湖南重点实验室，资源环境与安全工程学院，湘潭 411201；3. 中南大学 地球科学与信息物理学院，长沙 410083;4.湖南文理学院 洞庭湖生态经济区建设与发展湖南省协同创新中心，常德 415000)

重力场欧拉反褶积最优解提取

周 勇1，3，4， 曹书锦2,3， 侯萍萍2， 杨子龙2

(1. 湖南文理学院 资源环境与旅游学院，常德 415000；2. 湖南科技大学 页岩气资源利用湖南重点实验室，资源环境与安全工程学院，湘潭 411201；3. 中南大学 地球科学与信息物理学院，长沙 410083;4.湖南文理学院 洞庭湖生态经济区建设与发展湖南省协同创新中心，常德 415000)

在传统重力场欧拉反褶积中，单一构造指数难于表征多个异弱常源；而枚举构造指数易于导致欧拉解过度发散、欧拉解解集庞大且其中谬解极多。为此，在采用非预测欧拉反褶积方法，避免枚举构造指数的基础上，采用截断奇异值分解法解欧拉齐次方程，以评价欧拉解的不稳定性，在此基础上，构建估计函数以保留位场总场效应相对较弱的异常源。最后通过数值例子进一步表明了方法的有效性和可靠性。

欧拉反褶积； 最优解； 估计函数； 截断误差； 奇异值分解

0 引言

欧拉反褶积是一种快速高效且适应性强的位场解释方法。其以使用先验信息少，不需要准确的解释模型，在某一尺度大小的滑动窗口下，通过人为确定/枚举构造指数从而快速而有效地圈定出异常源的基本轮廓而著称。当多个不同形态的异常场并存时，难于使用单一常数或枚举构造指数表征多个异常源或复杂地质构造异常源，导致通过人工经验选取构造指数的难度加大。由于欧拉超定方程组条件数极大，易于导致欧拉解发散。因而通过枚举构造指数，常使得欧拉解解集庞大且其中谬解极多，导致后续分析处理工作量急剧增大[1-2]。因而如何从众多的欧拉解中分辨和确定最优解一直是困扰人们的一个难题[3-9]。

为有效地剔除欧拉解解集中的谬解和提取最优解[2-3, 10-17]，诸多学者开展了富有成效地研究。姚长利等[12]提出水平梯度滤波准则、距离约束评价准则和聚集度约束评价准则等方法，促进欧拉反演方法进入实用化阶段;鲁宝亮等[2, 13]利用欧拉反褶积建立的超定方程组，求解出一组构造指数，计算出构造指数的可信范围和最佳构造指数，然后利用最佳构造指数欧拉反演计算;Gerovska等[1]用微分相似变换对欧拉解奇异点处的空间坐标、构造指数和线性背景场进行分析以提取缪解，并在此基础上，以欧拉解标准差构造评价标准过滤欧拉解解集中的谬解;Beiki等[18]利用截断奇异值分解方法对误差相对较大的欧拉解进行剔除，以提升欧拉反褶积对磁源异常的确定精度;曹书锦等[5]将截断误差与核密度估计进行相关分析，确定构造指数的一维核密度估计曲线的第二个峰值处的构造指数为最优构造指数，但该方法并没有将欧拉解解集作为多维数据来处理。这导致存在相邻或相似异常源混叠时，难于确定哪些欧拉解标示着同一个异常源。

在欧拉反褶积中，使用单一构造指数，易于导致欧拉解解集趋于发散；而枚举构造指数易使欧拉解解集过于庞大，导致后续分析、处理工作难度增大。针对如何选取最优解的问题，笔者从欧拉超定方程组的条件数过大的问题出发，计算欧拉解的截断误差，分析了不同噪声水平与截断误差的关系，并进一步确定了在异常源的边界上及其异常源中心欧拉解的截断误差最小，即为最优解，通过数值例子进一步表明了方法的有效性。

1 欧拉反褶积反演

假设笛卡尔坐标系于点(x,y,z)存在一个孤立异常源，在观测点(x0,y0,z0)处的重力异常响应f可以写为：

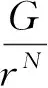
(1)

式(1)满足欧拉齐次方程，则

(2)

式中：∂f/∂x、∂f/∂y和∂f/∂z为f沿笛卡尔坐标系X、Y和Z三轴向的梯度，一般由离散傅里叶变换或离散余弦变换获得；B为消除区域背景场的影响，而引入的一个代表区域背景异常的参数。

将式(1)带入式(2)得到式(3)。

Nf(x-x0,y-y0,z-z0)+NB

(3)

特定地质构造有特定的构造指数，在求解式(3)时，可将构造指数作为一个预设参数，采用步长△N在0～3范围内枚举构造指数，获得欧拉解解集。随着步长△N不断地变小，欧拉解解集急剧增大，导致后续数据处理工作难度增大。为此，将构造指数N作为待求参数，将式(3)重写为式(4)。

(4)

式(1)基于剩余密度计算，背景场B数量级很小，故此这里将B略去。利用某一尺度wx的方形滑动窗口在勘察区域滑动，将滑动窗口内n个观测点的重力异常响应及其梯度，代入到式(4)中构建超定方程组，利用数值方法获取欧拉解，即异常源的空间位置信息(x,y,z)及构造指数N两部分。但由于式(4)本质上仍然是欧拉齐次方程，仍然存在对欧拉反褶积优解提取和缪解剔除的工作。

FitzGerald等[3]系统地给出了传统提取最优解的策略，但在实施上存在诸多限制或需要考虑的因素，如没有给出可靠的可信度评价原则或奇异值的上下限，也不能估计整个欧拉解解集的优良性或确定哪些相类似的解标示同一个异常源。由于系数矩阵条件数很大，欧拉解解集受噪声干扰及滑动窗口大小影响很大。为此，笔者引入误差估计方法对欧拉解进行评价，以对比在不同噪声和不同位置处的欧拉解的分布情况。

2 基于截断奇异值分解法的欧拉解

将滑动窗口内n个观测值f带入到式(4)中，把欧拉反褶积方程构成的方程组写为矩阵的形式：

Gm=d

(5)

由于式(5)为超定方程组，使得欧拉解易受如观测数据噪声、滑动窗口大小、异常源深度等干扰因素影响而扰动。为对欧拉解的误差进行估计，利用截断奇异值分解法对m的误差进行估计。首先对系数矩阵G进行奇异值分解

G=USVT

(6)

式中：U为n×n的酉矩阵；V为4×4的对角矩阵，其对角线上的四个元素为G的特征值；S=diag(σ1,…,σp,…,0,…)，为n×4的矩阵，且对角线上的奇异值有σ1≥σ2≥…≥σp≥0，p=4；向量u1、…、up和v1、…、vp分别对应于矩阵U与V中各列向量。

将式(6)带入到式(5)中，欧拉解可写为

m=V/SUd

(7)

此时，m的误差可由下式估计得到：

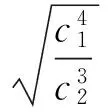
(8)

其中

(9)

其中：b=Ge=m-m*；e为残差；m*=G-1d。

为评价欧拉解稳定性，特设定一个估计函数以过滤欧拉解解集中的缪解[19-20]

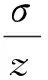
(10)

当欧拉反演对深度估计不准时，如两个异常源相互干扰，易于使得σr所表示的位置偏离异常源中心。基于截断误差的改进的估计函数写为式(11)。

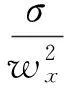
(11)

当σr大于某一特定的阈值σ0，便认为其过滤得到的欧拉解为最优解。

3 模型试验

3.1 算法验证

以重力正演解析解明确且构造指数易于确定的简单几何体(如立方体，其构造指数为2)构建地球物理模型，验证本文欧拉反演算法的正确性。在均匀半空间构造模型I：一个大小为200 m × 200 m × 300 m、顶板埋深为150 m、底板为350 m且剩余密度为0.3 g/cm3的异常体。该模型沿笛卡尔坐标系X、Y和Z三轴向的剖分数分别为32、32和16；测网大小为50 m × 50 m，观测点个数为32 × 32 = 1 024，观测点高度为地面上25 m。利用解析解计算简单规则模型重力异常响应f，进一步利用快速傅里叶变换计算重力响应f沿着笛卡尔坐标系沿三轴向的导数fx、fy、fz。在此基础上，应用欧拉反褶积方法计算异常源的空间位置信息(x,y,z)及构造指数N两部分。

如图 1所示，在欧拉反演解释中，一般将欧拉解逐点画于观测数据上，以标示异常源的分布情况。该立方体异常源的欧拉解均位置异常源中心，且构造指数的值分布于1.91～2.13之间，这与立方体异常源的构造指数的理论值一致，表明了本算法的正确性。

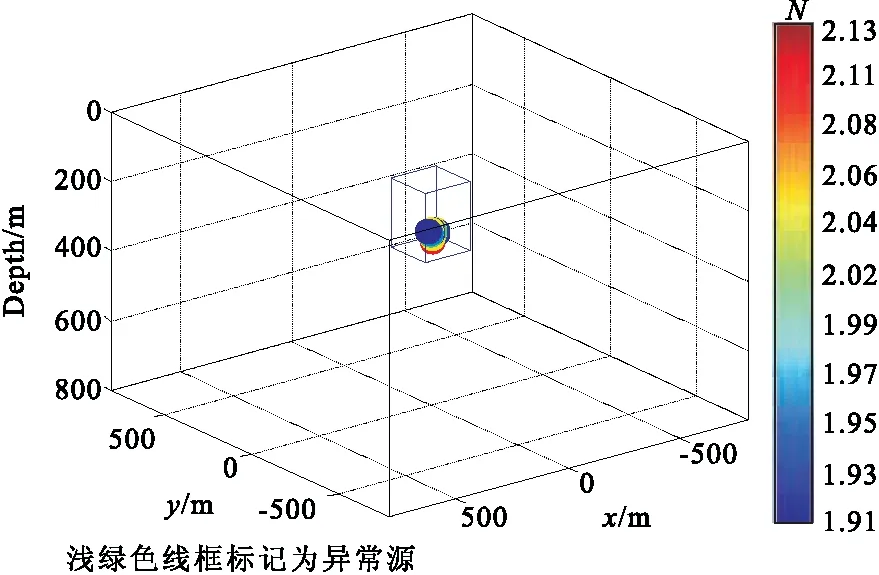
图1 孤立异常源欧拉解分布示意图(未添加噪声)Fig.1 Euler deconvolution solutions of isolated anomaly (without noise)

3.2 孤立异常源

在此基础上，为提取欧拉反褶积最优解，特从孤立异常源、同一深度和不同深度异常源等三个方面研究欧拉解的分布情况。由于欧拉齐次方程为超定方程，易于受观测数据所含噪声的影响,特在模型I正演结果内添加3%的高斯白噪声。

图 2为孤立异常源正演数据添加3%高斯白噪声后的欧拉解分布示意图。通过与图 1进行对比，虽然分布于异常体内部的构造指数值趋近于立方体构造指数的理论值，但分布范围从原有的1.91～2.13变为1.15～2.04。相比于图 1中在异常源外部没有任何缪解，而在图 2中出现大量缪解，表明观测数据的噪声将极大地导致欧拉反褶积的发散。

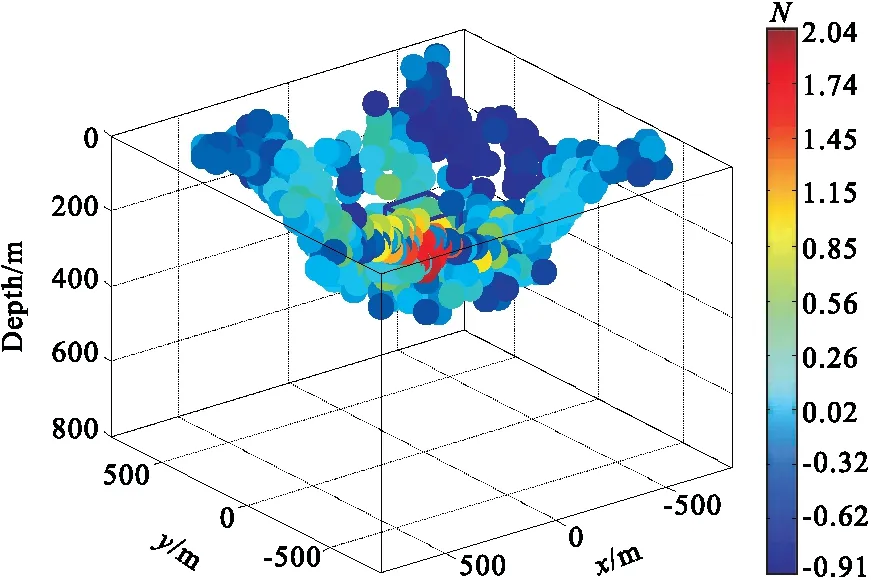
图2 孤立异常源欧拉解分布示意图 (添加3%噪声，未过滤)Fig.2 Euler deconvolution solutions of isolated anomaly (with 3% white Gaussian noise, before filtered)

图 3为基于截断误差估计的孤立异常源欧拉解的阈值示意图。从图3中可以看出，在异常源中心和异常源外部σr的差异性非常小，不利于过滤辨别及过滤欧拉反褶积缪解。主要由于当随着欧拉解远离异常源中心时(图 2)，其深度z逐渐变小，这导致由式(10)计算得到估计函数σr在异常源内部和外部的差异非常小。

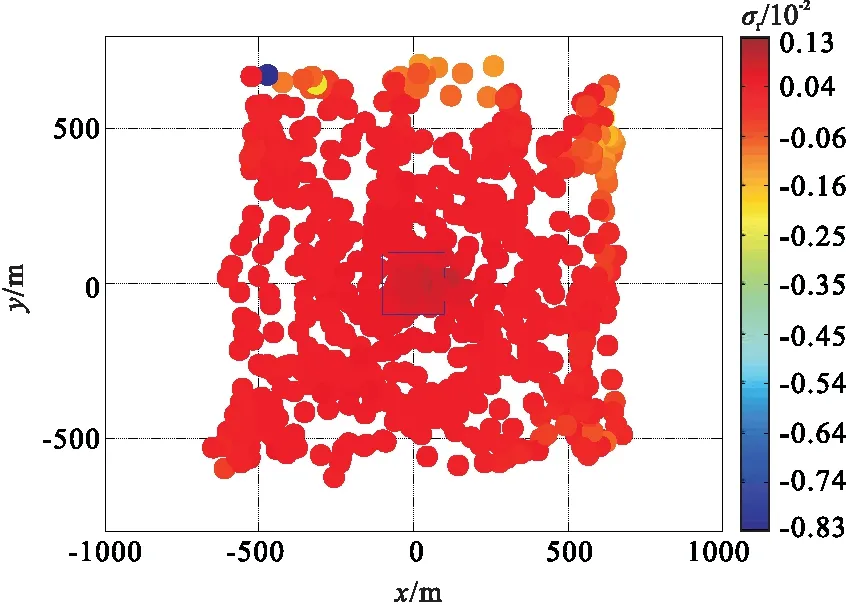
图3 估计函数阈值σr示意图Fig.3 Threshold value of estimation function σr

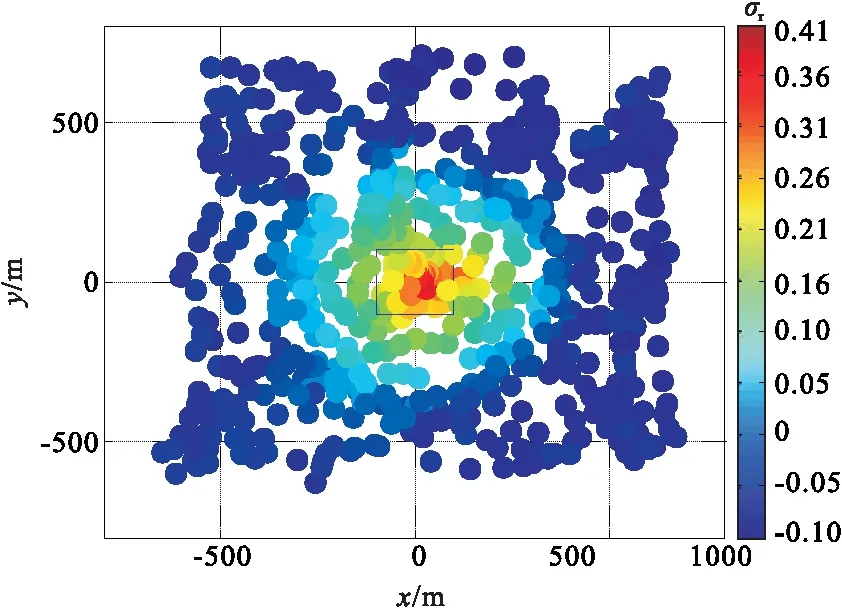
图4 改进的估计函数阈值示意图Fig.4 Threshold value of improved estimation function

图 4为基于截断误差估计的孤立异常源欧拉解的阈值示意图。相比于图 3，改进的σr在异常源外部和异常源内部的差异很大，这便于对欧拉解解集中谬解的剔除。

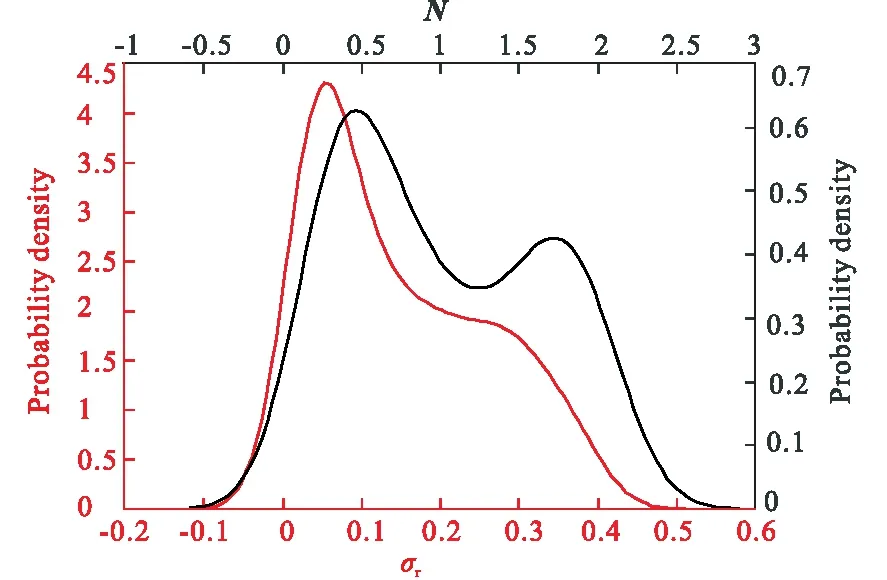
图5 构造指数及截断奇异值分解阈值的概率密度估计Fig.5 Probability density estimation of struct index and threshold of truncated singular value decomposition

为确定σ0，利用核密度估计分析截断奇异值分解阈值曲线和构造指数,并进行相关分析(图 5)，确定采用阈值σ0>0.2作为过滤欧拉解解中缪解的标准。如图 6所示，表明欧拉积解恰处于正演模型的内部中。

图6 欧拉解分布示意图 (添加3%高斯白噪声，过滤后)Fig.6 Euler deconvolution solutions (with 3% white Gaussian noise, before filtered)

从图 1和图 2中可以看出，在未对欧拉解进行过滤时，浅部的欧拉解受噪声干扰比较明显。因此采用估计函数σr以σ0=0.2作为阈值过滤欧拉反褶积缪解。过滤后的欧拉解恰位于异常源中心，这表明了估计函数σr的正确性。相比于传统基于构造指数的过滤策略，如以N<0、0.2、0.5等为标准，过滤欧拉解解中的缪解，采用估计函数σr以σ0=0.2作为阈值过滤欧拉解缪解，则能保留能标示异常源中心但N不接近2的,因而，本文算法更具有优势。

3.3 同一深度异常源

由于改进的估计函数σr与深度无关，故而需要对同一深度和不同深度模型进行对比分析。特构如下地球物理模型 II：由两个均为200 m × 200 m × 200 m，且剩余密度分别为0.3 g/cm3，质心分别为(-400 m, 0 m, 250 m)与(400 m, 0 m, 250 m)的立方体组成。该模型沿着笛卡尔坐标系三轴向的剖分数分别为32、32和16；测网大小为50 m × 50 m，观测点个数为32 × 32 = 1 024，观测点高度为地面上25 m。应用欧拉反演计算异常源异常空间(x,y,z)及构造指数N两部分。

图7 欧拉解分布示意图(未过滤)Fig.7 Euler deconvolution solutions (before filtered)

图8 欧拉解分布示意图(过滤后)Fig.8 Euler deconvolution solutions (after filtered)

图 7和图 8分别为欧拉解过滤前及过滤后分布示意图。由于两异常源的位场总场效应相当，欧拉解的分布呈现出一定的对称趋势。通过图7和图8的对比分析可以发现，采用估计函数σr以σ0=0.2作为阈值过滤欧拉反褶积缪解，能有效地标示两相邻异常源中心。

3.4 不同深度异常源

在上一算例研究的基础上，将其中一个异常源的质心移到(400 m, 0 m, 350 m)，而其他参数不变，以研究不同深度异常源对估计函数σr影响。

从图9可以看出，深部异常源受到浅部异常源的干扰，欧拉解有上延的趋势；未对欧拉解进行过滤时，表层的欧拉解受噪声干扰比较明显，浅部的欧拉解的分布很杂乱。

图10为不同深度异常源欧拉解过滤后分布示意图。相比于图1、图2和图8，由于深部异常源受到浅部异常源的干扰，构造指数N有逐渐变小的趋势，因而仅通过构造指数过滤欧拉反褶积缪解，可能会遗漏深部位场总场效应相对较弱的异常源。采用估计函数σr以σ0=0.2作为阈值过滤欧拉反褶积缪解，能有效地标示两相邻异常源中心。

图9 欧拉解分布示意图(未过滤)Fig.9 Euler deconvolution solutions (before filtered)

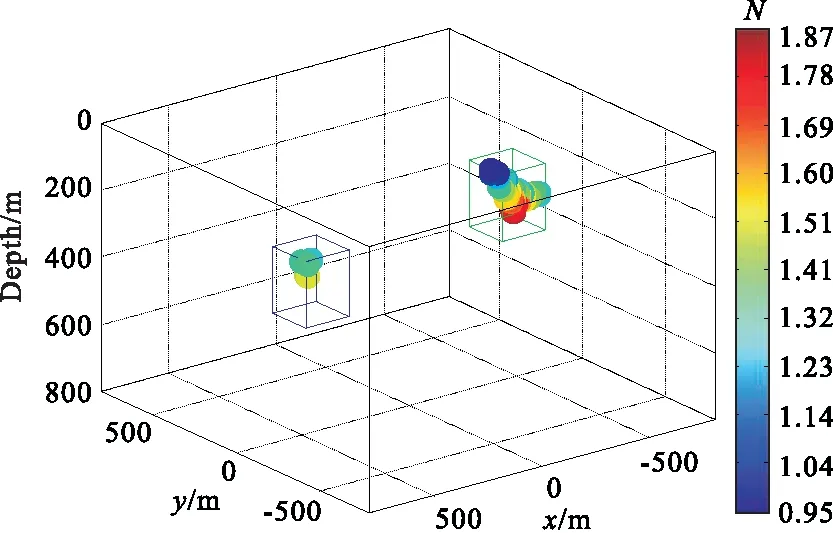
图10 欧拉解分布示意图(过滤后)Fig.10 Euler deconvolution solutions (after filtered)

4 结论与建议

通过对孤立异常源、同一深度和不同深度异常源基于估计函数σr的欧拉反演解释，得到如下结论：

1)由于欧拉齐次方程为超定方程，易于受观测数据所含噪声水平的影响，且深部异常源受到浅部异常源的干扰，构造指数N有逐渐变小的趋势，仅通过构造指数过滤欧拉反褶积缪解，可能会遗漏深部位场总场效应相对较弱的异常源。

2)在异常源中心和异常源外部原有估计函数σr的差异性非常小，不利于过滤辨别及过滤欧拉反褶积缪解。

3)改进估计函数σr能有效地标示同一深度和不同深度两相邻异常源中心，适应性强。

[1] GEROVSKA D, ARAúZO-BRAVO M. Automatic Interpretation of magnetic data based on euler deconvolution with unprescribed structural index[J]. Computers & Geosciences, 2003,29(8):949-960.

[2] 鲁宝亮, 范美宁, 张原庆. 欧拉反褶积中构造指数的计算与优化选取[J]. 地球物理学进展, 2009,24(3): 1027-1031.

LU B L,FAN M N,ZHANG Y Q. The calculation and optimization of structure index in euler deconvolution[J]. Progress in Geophysics, 2009, 24(3): 1027-1031.(In Chinese)

[3] FITZGERALD D,REID A,MCINERNEY P.New discrimination techniques for euler deconvolution[J].Computers and Geosciences,2004,30(5):461-469.

[4] DEWANGAN P,RAMPRASAD T,RAMANA M,et al.Automatic interpretation of magnetic data using euler deconvolution with nonlinear background[J].Pure and Applied Geophysics,2007,164(11):2359-2372.

[5] 曹书锦, 朱自强, 鲁光银. 基于自适应模糊聚类分析的重力张量欧拉解[J]. 中南大学学报(自然科学版), 2012,43(3): 1033-1039.

CAO SH J, ZHU Z Q, LU G Y.Gravity tensor euler deconvolution solutions based on adaptive fuzzy cluster analysis[J]. Journal of Central South University, 2012, 43(3): 1033-1039. (In Chinese)

[6] UGALDE H, MORRIS W. Cluster analysis of euler deconvolution solutions: New filtering techniques and geologic strike determination[J]. Geophysics, 2010,75(3): L61-L70.

[7] QUARTA T. Euler homogeneity equation along ridges for a rapid estimation of potential field source properties[J]. Geophysical Prospecting, 2009,57(4): 527-542.

[8] AGARWAL B, SRIVASTAVA S. Analyses of self-potential anomalies by conventional and extended euler deconvolution techniques[J]. Computers & Geosciences, 2009,35(11): 2231-2238.

[9] STAVREV P,REID A.Degrees of homogeneity of potential fields and structural indices of euler deconvolution[J].Geophysics,2007,72(1):1-12.

[10] HANSEN R, SUCIU L. Multiple-source euler deconvolution[J]. Geophysics, 2002,67: 525-535.

[11] MUSHAYANDEBVU M F, LESUR V, REID A B, et al. Grid euler deconvolution with constraints for 2D structures[J]. Geophysics, 2004,69(2): 489-496.

[12] 姚长利, 管志宁, 吴其斌, 等. 欧拉反演方法分析及实用技术改进[J]. 物探与化探, 2004,28(2): 150-155.

YAO C L, GUAN Z N, WU Q B, et al.An analysis of euler deconvolution and its improvement[J]. Geophysical and Geochemical Exploration, 2004, 28(2): 150-155. (In Chinese)

[13] 范美宁, 孙运生, 田庆君. 关于欧拉反褶积方法计算中的一点改进[J]. 物探化探计算技术, 2005, 27(2): 171-174.

FAN M N, SUN Y S, TIAN Q J. An improvement on calculation of euler decovolution[J]. Computing techniques for geophysical and geochemical exploration, 2005, 27(2): 171-174. (In Chinese)

[14] 史辉, 刘天佑. 利用欧拉反褶积法估计二度磁性体深度与位置[J]. 物探与化探, 2005, 29(3): 230-233.

SHI H,LIU T Y. The application of euler deconvolution to estimating depth and location of the 2-D magnetic body[J].Geophysical and Geochemical Exploration, 2005, 29(3): 230-233. (In Chinese)

[15] 范美宁, 江裕标, 张景仙. 不同数据用于欧拉方程的模型计算[J]. 地球物理学进展, 2008,23(04): 1250-1253.

FAN M N, JIANG Y B, ZHANG J X. Model calculation of euler’s equation for different data types[J]. Progress in Geophysics, 2008,23(4):1250-1253.(In Chinese)

[16] 习宇飞, 刘天佑, 杨坤彪, 等. 欧拉反褶积法用于井中磁测数据反演与解释[J]. 工程地球物理学报, 2008,5(2): 181-186.

XI Y F,LIU T Y,YANG K B,et al. The application of euler deconvolution to borehole magnetic surveys inversion and interpretation[J]. Chinese Journal of Engineering Geophysics, 2008, 5(2): 181-186.(In Chinese)

[17] 卞光浪, 翟国君, 刘雁春,等. 应用改进欧拉算法解算磁性目标空间位置参数[J]. 测绘学报, 2011,40(03): 386-392.

BIAN G L, ZHAI G J,LIU Y C, et al. Computation of spatial position parameters of magnetic object with improved euler approach[J]. Acta Geodaetica et Cartographica Sinica,2011, 40(3): 386-392.(In Chinese)

[18] BEIKI M.TSVD analysis of euler deconvolution to improve estimating magnetic source parameters: An example from the sele area, sweden[J].Journal of Applied Geophysics,2013,90:82-91.

[19] STAVREV P, GEROVSKA D, ARAUZO-BRAVO M. Depth and shape estimates from simultaneous inversion of magnetic fields and their gradient components using differential similarity transforms[J]. Geophysical Prospecting, 2009, 57(4): 707-717.

[20] THOMPSON D T. EULDPH: A new technique for making computer-assisted depth estimates from magnetic data[J]. Geophysics, 1982, 47(1): 31-37.

Extractionoptimalsolutionofeulerdeconvolutionforgravitydata

ZHOU Yong1,3,4, CAO Shujin2,3, HOU Pingping2, YANG Zilong2

(1.College of Resource Environment and Tourism, Hunan University of Arts and Science, Changde 415000, China;2.Hunan Provincial Key Laboratory of Shale Gas Resource Utilization, School of Resource Environment and Safety Engineering, Hunan University of Science and Technology, Xiangtan 411201, China;3.School of Geosciences and Info-physics, Central South University, Changsha 410083, China;4. Construction and Development of Dongting Lake Ecological Economic Zone of Hunan Synergy Innovation Center, Hunan University of Arts and Science, Changde 415000, China)

It is difficult to characterize multiple anomalies by a single structural index. Euler deconvolution's solutions is hugeous with divergent trend caused by enumerated structural index in traditional Euler decomposition. To overcome those problems, unprescribed Euler deconvolution method is introduced to avoid enumerate structural index, and a novel technology roadmap is proposed for estimating instability of Euler solution based on Euler equation of gravity data solving by truncated singular value decomposition method. A new estimation function is presented based on truncation error to filter the spray solutions. Numerical results show that the technology roadmap of Euler deconvolution is feasible, effective, and has better adaptability in this study.

optimal euler solution; Euler deconvolution; estimate function; truncation error; singular value decomposition

P 631.4

A

10.3969/j.issn.1001-1749.2017.05.03

2016-05-01 改回日期： 2017-06-09

国家自然科学基金(4147114，41374120);湖南省自然科学基金项目(14JJ7038, 2017JJ3069)；湖南科技大学博士科研启动基金(E51651)；湖南省教育厅科研项目(2010JD42)；湖南科技大学企业技术服务项目(D11646)；湖南科技大学SRIP项目(SYZ2017010)

周勇(1971-)，男，博士，副教授,主要从事地球物理勘探数据处理与反演研究等，E-mail：zhouyong_csu@163.com。

曹书锦(1983-)，男，博士,讲师,主要从事浅层地球物理正反演方法研究，Email:shujin.cao@163.com。

1001-1749(2017)05-0598-07