预测控制工程应用中预测时域的选取分析①

吴 博 罗雄麟 韦明辉 许 锋

(中国石油大学(北京)地球物理与信息工程学院)

预测控制工程应用中预测时域的选取分析①

吴 博 罗雄麟 韦明辉 许 锋

(中国石油大学(北京)地球物理与信息工程学院)

对现有的预测时域选取方法进行了总结，并且结合工程实际和理论分析，给出了预测控制算法中预测时域可取的范围。在这一范围内，可以快速简捷地选取所有可取的预测时域。最后，通过两个仿真实例分析了在预测时域可取范围内，不同条件下选取的预测时域对于控制性能的影响。

预测控制 预测时域 选取范围

PID由于算法简单、鲁棒性强和可靠性高被广泛应用于实际工业过程控制。但PID算法对于存在非线性、时变不确定性和数学模型不确定的系统往往达不到理想的控制效果。为了克服这些问题，出现了各种先进控制算法。预测控制算法由于对模型的宽容性(参数与非参数、线性或非线性)、有限时域滚动优化的有效性和在设计中可以方便地处理各种软硬约束而成为过程工业中应用最广泛的先进控制方法[1,2]。

20世纪80年代到90年代，随着预测控制方法在工业界越来越多的应用，各种预测控制算法也被总结提出，如模型算法控制(MAC)、动态矩阵控制(DMC)和广义预测控制(GPC)[3～5]。为了使预测控制算法体现其优良特性，各种预测控制的参数选取方法也被学者们所研究。学者们结合工程实际，根据动态响应情况和跟踪误差的分析给出了很多参数选取方法[6～8]。另外一些学者依据系统的稳定性和鲁棒性分析，给出了相应的预测控制器参数[9,10]。

在所有预测控制参数中，预测时域的选取对预测控制性能的影响最大。预测时域的选取是建立在采样时间的基础上的，若选取过小，虽然响应较快，但未必满足稳定性和约束条件[11]；若选取过大，动态过程虽然平稳却很缓慢，较大的预测时域会影响动态特性[12,13]。有些学者为了说明其优化方法的优越性，往往将预测时域选得极大，这显然是不合理的。笔者对前人的研究做了总结，结合工程实际和理论分析，给出了采样时间和预测时域可取的范围，并据此提出了一套简捷的预测时域选取方法。最后通过一个模型预测控制(MPC)和一个MPC-PID串级控制证明了笔者所提选取方法的有效性。

1 预测控制算法简介

DMC因基于阶跃或者传递函数模型而易于实现，是化工过程控制中最常采用的预测控制方法。因此笔者以DMC为例来说明预测控制参数的确定准则。

对于在单位阶跃作用下在N步后达到稳态的时不变SISO系统，阶跃响应{s1,s2,…,sN}构成系统的完整模型，预测输出为：

Y(k|k)=Y0(k|k)+AΔU(k|k)

(1)

则一般DMC算法性能指标为：

(2)

其中E(k|k)=Ys(k|k)-Y(k|k)为跟踪误差，Ys(k|k)为未来输出的参考值。

在无约束条件下，最小化式(1)的结果为：

ΔU(k)=(ATWA+R)-1ATWE0(k)

(3)

但控制问题都是有约束存在的，一般的约束有控制作用速率约束、控制作用物理约束和输出约束，其形式为：

ΔUmin≤ΔU≤ΔUmax

Umin≤U≤Umax

(4)

Ymin≤Y≤Ymax

结合性能指标式(1)和约束式(4)可以构成预测控制的最优化问题，通过二次规划可以求解上述最优化问题，求得ΔU(k)，但是每次当前k时刻，只执行最优控制序列ΔU(k)的第1项，下一时刻重新滚动计算优化问题。

2 预测时域的选取方法

预测控制方法出现了近40年时间，学者们为了提高控制性能，给出了很多参数选取方法。对于DMC算法，主要的参数有采样周期T、模型长度N、预测时域P及控制时域M等。笔者主要根据采样时间和模型长度来研究确定预测时域的可取范围。

2.1 采样时间和模型长度的确定

在预测控制算法中，采样周期T的选取首先必须遵循采样控制系统对采样周期的选取原则，即满足香农采样定理，并且符合被控对象的动态特性。对于采样周期的选取，已有了各种建议，如：对于单容对象，取T≤0.1Tσ，Tσ为对象的惯性时间常数。但对于预测控制算法，采样周期的选取还与模型长度N有着直接关系，通常为了使模型参数si(i=1,…,N)尽量完整地反映过程对象的动态信息，要求在动态响应时间tF后阶跃响应已近似稳态。

通常情况下，T选取得小可以提高精度并及时抑制干扰，但T选取得过小，会造成N值增高，使模型复杂度增加，并且太小的采样周期得到的控制作用无法在底层回路得到充分的响应。因此对于过程量的控制，模型长度N一般取在25～50。由于tF为常数，可确定模型维数N，也可确定采样周期T。

2.2 预测时域上限的确定

预测时域P是根据采样周期T而选取的。根据上述方法确定了T的范围后，Tmin所对应的可选取的最大预测时域是P1max，Tmax所对应的可选取的最大预测时域为P2max，并且有：

(5)

对于可选取采样周期范围Tmin≤T≤Tmax内所对应的最大的预测时域曲线Pmax如图1所示。这样就确定预测时域P的上限。当P取为它能取值的上限时，已经接近稳态，这样导出的控制率比较稳定，但系统的动态响应近似于系统的自然响应，影响系统的快速性，无法体现出预测控制的优势。并且在文献[12,13]中也分析论证了P选取得越大，控制效果未必越好。

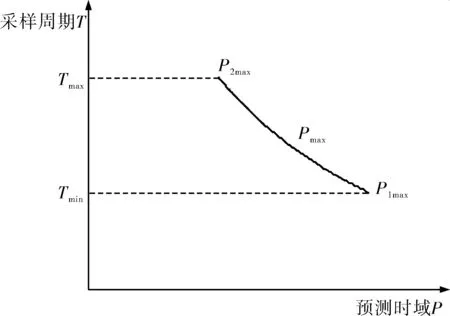
图1 预测时域选取上限曲线

2.3 预测时域下限的确定

首先为了满足物理意义，预测时域P选取得要比控制时域M大，即P≥M+1。

为了使预测控制稳定，P不能选得太小。从20世纪70年代末预测控制方法出现以来，研究者们对于其稳定性的研究已经给出了较成熟的理论。对于DMC算法，最常用的稳定性理论为在控制增量变化不大的范围内若在P步内选取的动态过程方向与最终稳态方向一致，则预测控制系统为稳定的，由此控制时域M可确定预测时域选取的下限，定义符合条件的关系曲线为Pmin1(T)。

在工程应用中，一般取P步要覆盖部分动态响应过程，即应至少覆盖反向响应部分和时滞：

(6)

曲线Pmin1(T)和Pmin2(T)有3种情况(图2，阴影区域即预测时域可以选取的最大范围。)：

a. 一般情况，Pmin1(T)在Pmin2(T)右侧，如图2a所示；

b. 有较大时滞时，曲线Pmin1(T)和Pmin2(T)相交，如图2b所示；

c. 当时滞非常大时，Pmin1(T)在Pmin2(T)左侧，如图2c所示。

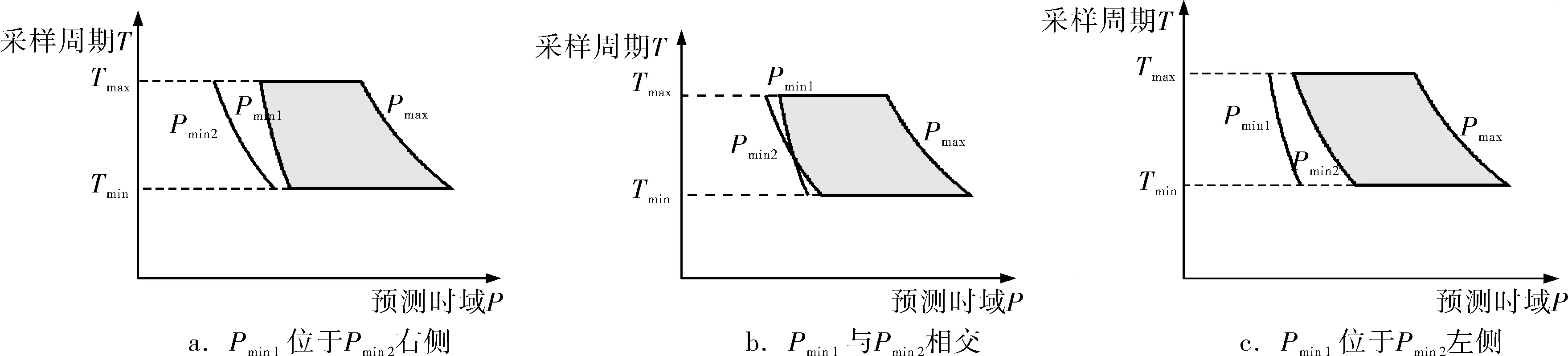
图2 预测时域可选取区域

根据上述分析，把Pmin1(T)和Pmin2(T)所确定的预测时域选取下限的曲线定义为Pmin(T)。这样即可根据曲线Pmax(T)、Pmin(T)与采样周期T的取值范围做出预测时域可以选择的区域，如图2所示。预测时域P可以选取的值为该区域内任一整数，与采样周期相对应。

在实际应用中，一般不会将预测时域取到上限值或者下限值，取上限值的缺点已在2.2节讨论过。当P值取得过小时，对于有约束的预测控制，每步求得的控制率会接近约束的上下限。而预测控制方法应用时往往采用透明控制，即上层为预测控制回路，底层为PID回路。当控制率变化过大时，底层回路无法完全响应，会影响控制效果。

上述讨论均是针对单变量系统的，但是该方法很容易推广到多变量系统。对于多变量系统，在工程中为了应用简捷，往往会对不同变量选取相同的采样周期，而且预测时域也会尽量选取的相同。

按上述方法绘制每个变量的预测时域-采样周期区域图。因为对于不同变量要选取相同的采样周期，而采样周期的交集为Tmini≤T≤Tmaxj，Tmini为所有变量可取采样周期下限中的最大值，Tmaxj为所有变量采样周期可取上限中的最小值，因此取采样周期的交集为多变量系统所有变量采样周期可选择区域中的公共部分。

为了方便讨论，对每个变量预测时域下限的选取按照图2a的方法选取，此时对于每个变量，曲线Pmax、Pmin都为一簇平行的双曲线，P取值为双曲线与采样周期范围包围区域内的整数。

对每个变量绘制预测时域-采样周期区域图，在采样周期的交集范围Tmini≤T≤Tmaxj内所包含的公共区域即多变量系统预测时域P可以选取的范围，如图3a阴影部分所示。

图3 多变量系统预测时域可选取区域

对于某些特殊的情况，例如TITO系统，最大动态响应时间为50min，最小动态响应时间为25min。对于此系统按照上述方法选取的预测时域-采样周期的交集不是一个区域，而是一条直线，如图3b所示。若要选取相同的预测时域P，则需从直线范围中选取。综上所述，对于预测时域的选取可以归结为以下几步：

a. 按照2.1节中的方法确定模型维数和采样周期；

b. 根据采样周期的范围按照2.2节的方法确定预测时域的上限；

c. 根据2.3节的方法确定预测时域选取的下限；

d. 对此变量绘制如图2所示的区域图；

e. 对于多变量系统，对每个变量重复以上步骤，取所有区域的交集。

如果各变量的预测时域-采样周期区域无重合，则表明各变量的动态响应时间差别过大，存在多个时间尺度，此时的系统为病态系统，因此无法选择统一的采样周期，此时应对整个系统进行分解，分解为不同时间尺度的多个子系统，再分别进行预测控制系统的采样周期和预测时域设计。

3 实例研究

假设一个TITO系统的传递函数为：

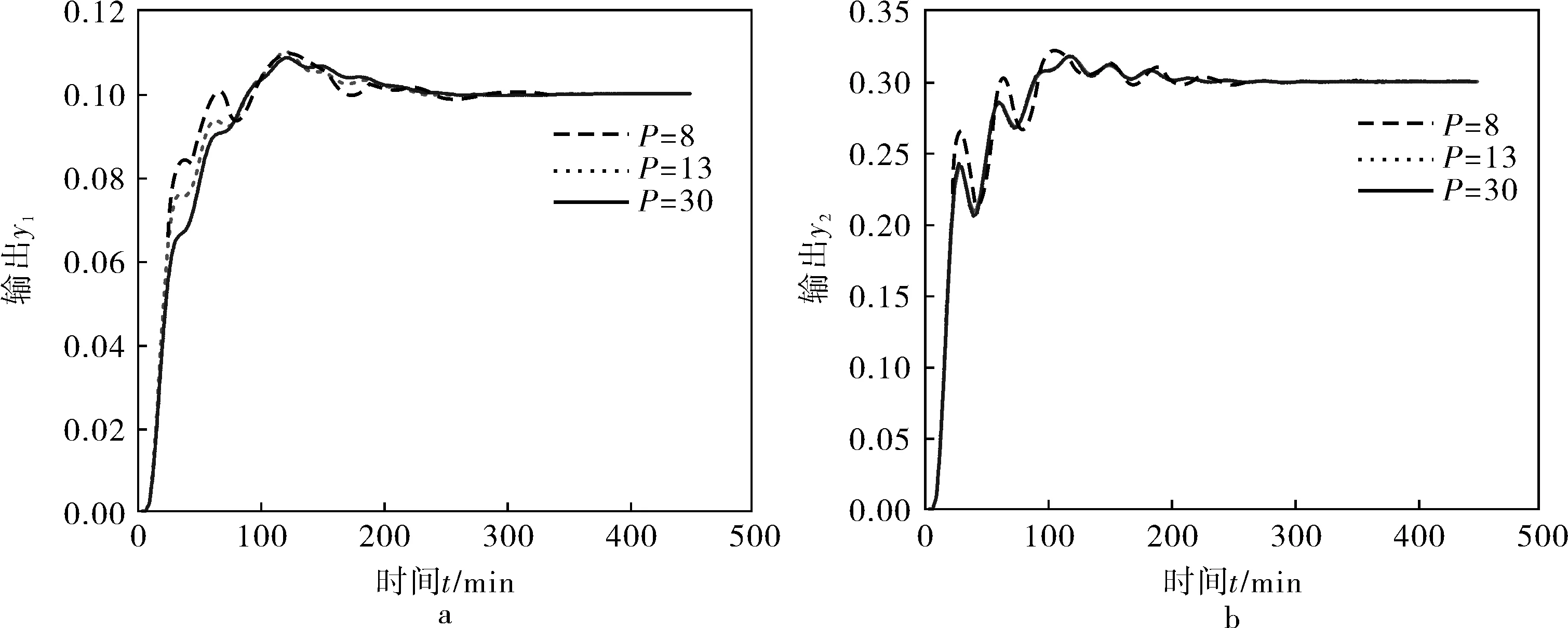
通过阶跃测试，变量y1的动态响应时间为100min，变量y2的动态响应时间为80min。将N分为25～50，则采样周期的取值范围为2.0～3.2min。由于Pmin1

图4 TITO系统预测时域可选取区域

当采样周期T=2.0min时，按照图4所示区域，预测时域最小可选取P=13。在此区域内分别选取预测时域P为13、18、30和45进行仿真实验，结果如图5所示。

图5 采样周期为2min时的响应曲线

由图5可见，选取的预测时域的响应曲线都符合要求。当按照上文方法选取最小可取的P=13时，响应较快，但波动较大。适当增加P，选取P=18，可得较平稳的曲线，并且不影响响应速度。当P较大时，选取P=30、P=45，可以看出此时响应曲线已基本一致，而且相比于P=18时的响应曲线，动态特性并未提升，反而增大了运算负担。

当采样周期T=3.0min时，按照图4所示区域，预测时域最小可选取P=8。在此区域内分别选取预测时域P为8、13和30进行仿真实验，结果如图6所示。可以看出，选取的3个预测时域的控制效果都可以接受。同时P=13和P=30的响应曲线已基本重合，结合图5中P=18、P=30和P=45的情况，分析可知当预测时域能覆盖一定区域后继续增大预测时域已无意义，只会增加运算负担，并且对于某些波动，预测时域选取太大会使动态响应变慢，不利于快速跟踪目标值。

图6 采样周期为3min时的响应曲线

在本例中，采样周期选取2.0min和3.0min，可以看出二者区别较小，说明了在合理范围内采样周期选取得不同对系统无较大影响。

4 结束语

对预测控制方法中预测时域的选取方法进行了讨论，在总结前人研究经验的基础上，给出了预测时域可选取的区域，在此区域内可以方便快捷地找出可选取的预测时域。该方法对于单变量和多变量系统同样适用。通过仿真实例验证了该方法的有效性。

[1] Alpbaz M, Karacan S, Cabbar Y，et al. Application of Model Predictive Control and Dynamic Analysis to a Pilot Distillation Column and Experimental Verification[J].Chemical Engineering Journal, 2002, 88(1-3): 163～174.

[2] Brian F J.Model Predictive Control—Building a Bridge between Theory and Practice with Direction-dependent Dynamic Responses[J]. Computers and Chemical Engineering, 2006, 30(10-12): 1426～1435.

[3] Rouhani R, Mehra R K. Model Algorithmic Control (MAC): Basic Theoretical Properties[J]. Automatica, 1982, 18(4):401～414.

[4] Cutler C R, Ramaker B L. Dynamic Matrix Control—A Computer Control Algorithm[C].Proceedings of Joint Automatic Control Conference.Piscataway:IEEE, 1980: WP5-B.

[5] Clarke D W, Mohtadi C, Tuffs P S. Generalized Predictive Control[J]. Automatica, 1987, 23(2): 137～160.

[6] Likar B, Kocijan J.Predictive Control of a Gas-Liquid Separation Plant Based on a Gaussian Process Model[J].Computers and Chemical Engineering, 2007, 31(3): 142～152.

[7] Qin S J, Badgwell T A. A Survey of Industrial Model Predictive Control Technology[J].Control Engineering Practice, 2003, 11(7): 733～764.

[8] Muske K R, Badgwell T A. Disturbance Modeling for Offset Free Linear Model Predictive Control[J].Journal of Process Control, 2002, 12(5): 617～632.

[9] James B R, Kenneth R M.The Stability of Constrained Receding Horizon Control[J].IEEE Transactions on Automic Control, 1993, 38(10): 1512～1560.

[10] Mosca E, Zappa G, Lemos J M. Bartlett, Robustness of Multi-predictor Adaptive Regulators:MUSMAR[J].Automatica, 1989, 25(4): 521～530.

[11] Rahul S, Douglas J C, Godfrey K R.A Novel Tuning Strategy for Multivariable Model Predictive Control[J].ISA Translations, 1998, 36(4): 273～280.

[12] Clarke D W, Scattolini R. Constrained Receding-horizon Predictive Control[J].IEE Proceedings D-Control Theory and Applications, 1991, 138(4): 347～354.

[13] Mayne D Q, Rawlings J B, Rao C V,et al. Constrained Model Predictive Control: Stability and Optimality[J]. Automatica,2000, 36(6): 789～814.

AnalysisofSelectingPredictiveHorizonsinEngineeringofModelPredictiveControl

WU Bo, LUO Xiong-lin, WEI Ming-hui, XU Feng

(CollegeofGeophysicsandInformationEngineering,ChinaUniversityofPetroleum(Beijing))

The existing selection methods for the prediction horizon were summarized. Through having the engineering practice considered and theoretical analysis implemented, the prediction horizon’s selectable range in the predictive control algorithm was presented and within this range, all selectable prediction horizons can be chosen simply and directly. Through two simulation examples, the influence of prediction horizon selected in desirable ranges and under different conditions on the control performance was analyzed.

predictive control, prediction horizon, selectable range

吴博(1987-)，博士研究生，从事化工系统工程与过程控制的研究。

联系人罗雄麟(1963-)，教授，从事控制理论与过程控制、化工系统工程及机器学习等的研究，luoxl@cup.edu.cn。

TP273

A

1000-3932(2017)06-0553-06

2016-10-20，

2017-05-11)