一种基于加权平均的改进型小波阈值降噪算法①

刘书俊 李生林 蒋 明 宋志强 毕金友

(1.中国人民解放军后勤工程学院；2.76166部队)

一种基于加权平均的改进型小波阈值降噪算法①

刘书俊1李生林1蒋 明1宋志强1毕金友2

(1.中国人民解放军后勤工程学院；2.76166部队)

通过分析传统硬、软阈值小波降噪算法的原理和特点，提出一种改进型小波阈值降噪算法。该算法基于加权平均原理，结合了硬、软阈值降噪的优点，克服了硬阈值函数在阈值处不连续的缺点，使重构信号具有更加良好的光滑度；同时克服了软阈值函数存在固定偏差的不足，提高了重构精度，优势明显。通过实验对传统硬、软阈值小波降噪算法与改进型小波阈值降噪算法进行了对比分析，结果表明：改进型小波阈值降噪算法的降噪效果更好，信噪比更高，均方根误差更小。

小波阈值降噪 磁记忆检测 加权平均 硬、软阈值

在信号处理领域，小波变换是一种全新的分析方法，具有良好的时频局部化特性，即在低频部分具有较高的频率分辨率和较低的时间分辨率，而在高频部分具有较高的时间分辨率和较低的频率分辨率[1,2]。由于小波可以提供一个随频率改变的“时间-频率”窗口，是信号处理的理想工具，因此也被誉为“数学显微镜”[3]。由于真实信号和噪声的小波系数在不同尺度上具有不同的性质，因此，小波阈值降噪实际上就是根据先验性知识，进一步构造相应的处理规则，最后在小波域采取相应的数学处理方法对含噪信号的小波系数加以处理[4,5]。在实践中，以Donoho提出的硬、软阈值小波降噪算法应用最广[6]，该算法原理简单、计算量小，但由于它自身存在缺陷，降噪效果还不够理想。因此，笔者提出一种基于加权平均原理的改进型小波阈值降噪算法。

1 硬、软阈值小波降噪算法

1.1 算法原理

在硬、软阈值小波降噪算法中，软阈值函数为：

(1)

硬阈值函数为：

(2)

式中T——系数处理的阈值；

Wj,k——含噪信号经过小波变换后的小波系数；

图1、2分别为硬、软阈值函数图形，其中x表示阈值化处理之前的小波系数，y表示经过阈值化处理的小波系数。

图1 硬阈值函数

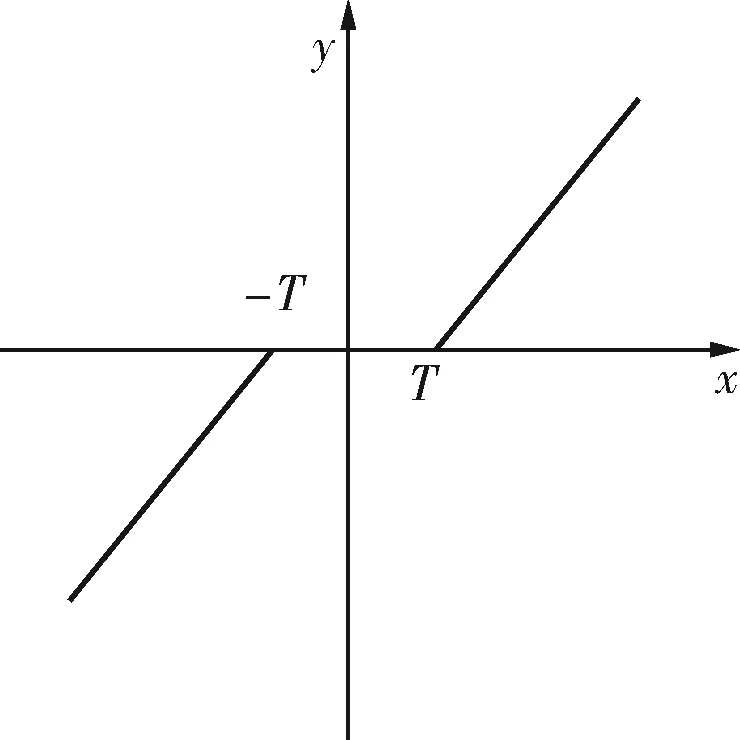
图2 软阈值函数

硬、软阈值方法自身具有一定的优点，但仍然存在一些缺陷：虽然软阈值算法处理的小波系数整体连续、光滑性好，但对于大于阈值的小波系数采取恒定压缩的方式，自然会损失一些有用的高频信息，从而影响重构信号的真实性；硬阈值算法可以避免软阈值的恒定偏差，但是由于小波系数在阈值T处是不连续的，这不可避免地会给重构信号带来一些附加振荡，使重构后信号的光滑度变差。因此，如果直接使用软阈值或硬阈值函数对信号进行降噪处理，可能无法获得理想的降噪效果[7,8]。

1.2 阈值函数的改进

为了有效弥补以上方法的不足，在硬、软阈值的基础上对阈值函数进行改进，引入权重指标，使用加权平均法，将硬、软阈值函数用加权平均的方法结合起来。令阈值函数为：

(3)

其中，α=ab；b=-(|Wj,k|-T)2/n2；α为加权因子；a和n为常数，且a>1，a是一个与信号有关的常数，可通过实验确定。

图3 改进后的阈值函数

2 算法验证

采用MFL-4032漏磁/磁记忆检测仪对一段长1 000mm的管道进行磁记忆检测[9]，为简化试验过程，采用双通道磁记忆检测探头进行检测。该管道共有9处裂纹，分别位于L1=136mm、L2=181mm、L3=322mm、L4=372mm、L5=526mm、L6=569mm、L7=752mm、L8=776mm、L9=959mm处。检测所得原始信号如图4所示，图5为相应的梯度曲线。

图4 检测信号曲线

图5 信号梯度曲线

根据俄罗斯动力诊断公司关于应力集中区或缺陷的判定准则[10,11]，对比分析检测信号曲线改变符号且过零点和曲线梯度值极大值，由于信号被噪声干扰，检测信号曲线存在较多峰值毛刺，严重影响对信号过零点的标示；同时，由于该磁记忆信号本身较为复杂，包含较多的噪声成分，此时的曲线梯度变化实际上不能反映真实的磁记忆信号梯度变化趋势，在这种情况下，梯度曲线本身也就失去了分析的意义。因此，由于噪声的干扰，导致无法根据应力集中区或缺陷的判定准则对应力集中位置或缺陷位置进行判定。

2.1 硬、软阈值小波降噪效果分析

将信号进行硬、软阈值小波降噪，由于软阈值降噪效果与硬阈值降噪效果基本相同，此处仅以软阈值为例进行说明。

图6、7分别为图4所示的磁记忆检测信号经过小波软阈值降噪后的曲线和相应的梯度曲线，其中，小波函数选用DB2小波，分解层数J=3。观察磁场强度法向分量Hp(y)，基于小波软阈值的磁记忆信号降噪可以消除部分噪声的影响，磁记忆信号曲线峰值毛刺大量减少，可以明显地看出曲线在L为181、371、529、565mm处过零点，在上述位置，磁记忆信号的梯度值也存在极大值，因此根据磁记忆检测判定准则，可以初步判定钢管以上位置存在应力集中或缺陷。但在100～150mm、315～330mm、725～800mm、925～970mm处，可以很明显地看出，由于采用的降噪算法存在局限性，导致降噪效果不够理想，磁记忆信号仍然存在峰值毛刺的干扰，光滑度不好，从而导致无法进一步对应力集中或缺陷位置进行判定。

图6 软阈值降噪后信号曲线

图7 软阈值降噪后信号梯度曲线

2.2 改进型算法降噪效果分析

采用改进型算法对信号进行降噪，得到降噪后的信号曲线和梯度曲线如图8、9所示。

图8 改进型算法降噪后信号曲线

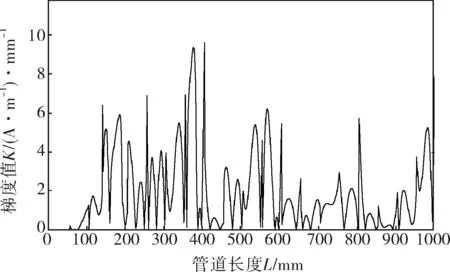
图9 改进型算法降噪后信号梯度曲线

对比采用软阈值降噪后的信号曲线及其梯度曲线(图6、7)，可以看出，改进型算法降噪效果明显优于小波阈值降噪。磁记忆信号经过改进型降噪后，波形平滑，基本消除了峰值毛刺的干扰，无相位失真和信号损失，有效抑制了噪声，信号梯度变化也可以很好地指示钢管应力集中区域。根据俄罗斯动力诊断公司的定性判断应力集中规则，磁记忆信号曲线在L为136、181、324、371、529、565、750、777、958mm处过零点，在上述位置，磁记忆信号曲线的梯度值K均存在极大值。因此，根据磁记忆判定准则，很容易判定管道在上述位置存在应力集中或缺陷，考虑到检测误差等人为因素的影响，这样的检测结果与实际情况是基本吻合的。

信号降噪效果可以采用信噪比(SNR)和均方根误差(RMSE)来评价[12]。其中：

(4)

(5)

式中N——信号采样点数；

s(n)——降噪前信号；

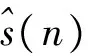
软阈值算法和改进型算法的信噪比与均方根误差对比见表1。可以看出，改进型算法的信噪比和均方根误差指标均优于软阈值算法，具有明显的优势。

表1 两种降噪算法的性能指标对比 dB

3 结束语

基于加权平均的改进型小波阈值降噪算法，结合了硬、软阈值降噪算法的优点，用MFL-4032漏磁/磁记忆检测仪对一段长1 000mm的管道进行磁记忆检测，结果表明：改进型算法克服了硬阈值函数在阈值处不连续的缺点，使重构信号具有更加良好的光滑度；同时克服了软阈值函数存在固定偏差的不足，提高了重构精度。改进型算法的降噪效果显著，并且提高了降噪后信号的信噪比，减少了信号的失真与振荡。

[1] 张建,杨娜,郑修凯,等.高速列车经过时跨线天桥表面风压小波分析[J].振动与冲击,2015,34(4):53～58.

[2] 郭健,查吕应,庞有超,等.基于小波分析的深基坑地表沉降预测研究[J].岩土工程学报,2014,36(z2):343～347.

[3] 李力,魏伟,唐汝琪,等.基于改进S变换的煤岩界面超声反射信号处理[J].煤炭学报,2015,40(11):2580～2586.

[4] 李明,陈卫忠,杨建平.隧道结构在线监测数据分析方法研究[J].岩土力学,2016,37(4):1208～1216.

[5] 曲巍崴,高峰.基于噪声方差估计的小波阈值降噪研究[J].机械工程学报,2010,46(2):28～33.

[6] 苏文胜,王奉涛,朱泓,等.双树复小波域隐Markov树模型降噪及在机械故障诊断中的应用[J].振动与冲击,2011,30(6):47～52.

[7] 魏振春,王婿,徐娟.基于改进阈值自适应冗余小波的振动信号去噪[J].计算机仿真,2014,31(11):192～197.

[8] 贺岩松,刘程,徐中明,等.基于软阈值和遗传自适应阈值的车辆制动信号的联合小波去噪[J].汽车工程,2014,36(6):703～708.

[9] 陈海龙,王长龙,朱红运.基于磁梯度张量的金属磁记忆检测方法[J].仪器仪表学报,2016,37(3):602～609.

[10] Doubov A A.Development of a Metal Magnetic Memory Method[J].Chemical and Petroleum Engineering,2012,47(11):837～839.

[11] 任吉林,林俊明,任文坚,等.金属磁记忆检测技术研究现状与发展前景[J].无损检测,2012,34(4):3～11.

[12] 陶珂,朱建军.多指标融合的小波去噪最佳分解尺度选择方法[J].测绘学报,2012,41(5):749～755.

AnImprovedWaveletThresholdDe-noisingAlgorithmBasedonWeightedAverageMethod

LIU Shu-jun1, LI Sheng-lin1, JIANG Ming1, SONG Zhi-qiang1, BI Jin-you2

(1.PLALogisticsEngineeringUniversity; 2.No.76166TroopofPLA)

Basing on analyzing the principle and characteristics of conventional hard and soft threshold de-nosing algorithms, an improved wavelet threshold de-noising algorithm was proposed, which has weighted average method based and advantages of the classic soft and hard threshold algorithms adopted and the hard threshold’s shortcoming such as the discontinuousness at threshold point overcome to make the reconstruction signal become into smoothness; meanwhile, this algorithm solves the fixed differential existed in the soft threshold meth-

刘书俊(1985-)，讲师，从事电磁无损检测技术的研究，jjxyliushujun@163.com。

TH865

A

1000-3932(2017)03-0239-05

(Continued on Page 318)

2016-05-23，

2016-12-12)