“等可能条件下的概率”易错点

王 芳

“等可能条件下的概率”易错点

王 芳

概率问题在每年中考中都占有不可忽略的地位，但是不少同学在计算概率时常会犯一些错误，导致失分，令人痛心.下面就同学们在概率问题中出现的常见错误举例加以分析.

易错点1 对等可能性理解不透彻

例1 判断下列各试验的结果哪些具有等可能性.

（1）抛掷一枚均匀的正方体骰子，面朝上的点数是奇数与面朝上的点数是偶数的结果；

（2）抛掷一颗图钉，顶尖朝上和朝下的结果；

（3）一只不透明的袋中装有3个红球和5个蓝球，这些球除颜色外都相同，搅匀后从中任意摸出一个球，出现红球和蓝球的结果.

【错解】（1）（2）（3）的试验结果都具有等可能性.

【正解】（1）的试验结果具有等可能性，（2）（3）两个试验结果不具有等可能性.

【错解辨析】抛掷一枚均匀的正方体骰子，面朝上的点数是奇数和偶数各有3种等可能的结果，所以试验（1）的结果具有等可能性.因为图钉不均匀，在抛掷中钉尖朝上和朝下的机会不均等，所以试验（2）的结果不具有等可能性.错解认为抛掷的图钉只有钉尖朝上或朝下两种结果，所以试验的结果具有等可能性.从一只装有3个红球和5个蓝球的袋子中任意摸出一个球有8种等可能的结果，而从中摸出红球和蓝球的结果出现的机会不均等，所以这个试验的结果不具有等可能性.错解认为袋中有两种颜色的球，所以摸到每种颜色的球的机会是均等的，所以这个试验的结果具有等可能性.

易错点2 求概率时忽略等可能条件

例2 已知甲袋中有2个红球，1个白球，乙袋中有1个红球，1个白球，从甲、乙两袋中各摸出一个球，摸出的两个球都是红球的概率是多少？（两种球只有颜色不同.）

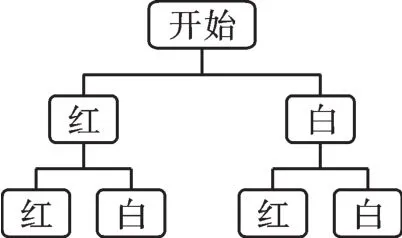
【错解】用树状图列出所有可能的结果如下图所示.从树状图可以看出一共有4种等可能的结果，其中两个球都是红球的结果有1种，所以摸出的两个球都是红球的概率为

【正解】分别用白、红1、红2表示甲袋中的3个球，用树状图列出所有可能的结果如下图所示，从树状图可以看出一共有6种等可能的结果，其中两个球都是红球的结果有2种，所以摸出的两个球都是红球的概率为

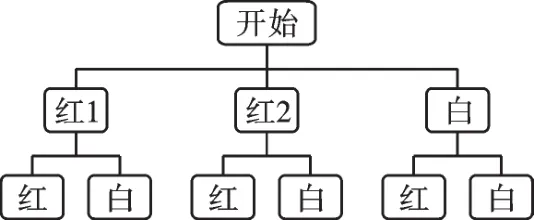
【错解辨析】甲袋中有2个红球、1个白球，故摸出红球和白球的可能性不相同.错解认为只有两种颜色的球，摸出红球和白球的可能性相同，从而造成解题错误.应将甲袋中的两个红球编号，编号为红1、红2，这样摸出白球、红球1、红球2才是等可能的.利用表格或树状图求概率直观形象，但是有时由于考虑问题不全面，常会出现遗漏，造成解题错误，因此在列表或画树状图时，一定要全面考虑，将所有可能出现的结果都列出来，做到不重不漏.

易错点3 审题不清

例3 不透明的口袋里装有白、黄、蓝三种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为

（1）试求袋中蓝球的个数；

（2）第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表法，求两次摸到的球都是白球的概率.

经检验，x=1是原方程的解，所以蓝球有1个.（2）画树状图如图所示.

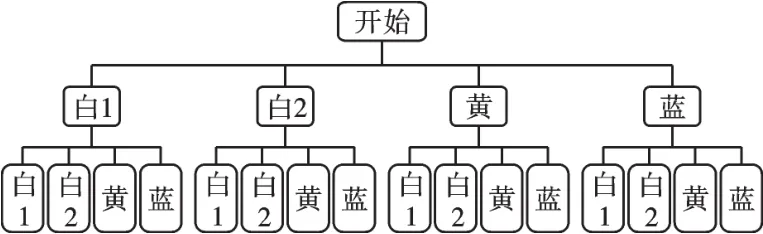
经检验，x=1是原方程的解，所以蓝球有1个.（2）画树状图如图所示.故两次摸到的球都是白球的概率

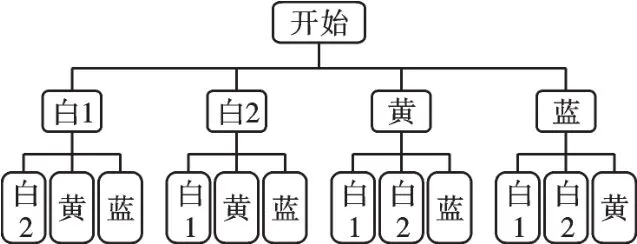
【错解辨析】题目中明确要求“第一次任意摸一个球（不放回）”就意味着第二次不可能摸到第一次已摸出的球.所以认真审题是解题的关键，忽略任意一个小的细节都会造成整个题目的错解.

小试牛刀

1.如图，电路图上有四个开关A、B、C、D和一个灯泡，闭合开关D或同时闭合开关A、B、C都可使灯泡发光.

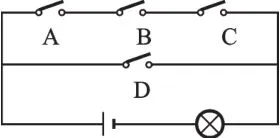
（1）任意闭合其中一个开关，则小灯泡发光的概率为多少？

（2）任意闭合其中两个开关，请用树状图或列表的方法求出小灯泡发光的概率.

2（.2015·株洲）从2，3，4，5，6中任意选两个数，记作a和b，那么点（a，b）在函数图像上的概率是多少？

3.（2015·荆门）在排球训练中，甲、乙、丙三人相互传球，由甲开始发球（记作为第一次传球），则经过三次传球后，球仍回到甲手中的概率是多少？

（作者单位：江苏省常州市金坛区第二中学）