C n中加权解析Lipschitz空间上复合算子的有界性
2017-11-01张彦林肖建斌高智娟
张彦林,肖建斌,高智娟
(杭州电子科技大学理学院,浙江 杭州 310018)
Cn中加权解析Lipschitz空间上复合算子的有界性
张彦林,肖建斌,高智娟
(杭州电子科技大学理学院,浙江 杭州 310018)
单位圆盘上的加权Lipschitz空间中复合算子的有界性与紧性问题已有文献探究,并给出了复合算子的有界与紧性的充要条件;但一直未见文献讨论Cn中加权解析Lipschitz空间上复合算子的有界性问题,刻画了Cn中加权解析Lipschitz空间的特性,并利用空间中诱导距离的性质给出了复合算子Cφ在加权解析Lipschitz空间上为有界算子的充要条件.
单位球;加权Lipschitz空间;复合算子;有界性
0 引 言
复合算子有界性的问题给函数论中的古老课题赋予了新的方法,为函数论算子代数的研究带来了重要的契机.1968年,Eric N.开始将复合算子作为解析函数空间上的线性算子进行研究,近几十年来,对于复合算子有界性问题已得到广泛研究.其中,Konstantin M.D.等[1]对单位圆盘上的Lipschitz空间中复合算子的有界性与紧性问题进行了探究,并给出了复合算子有界与紧算子的充要条件;戴济能[2]对单位球体中Lipschitz空间上的加权复合算子也进行了研究,并给出了加权复合算子有界性与紧性的充要条件.本文研究加权解析Lipschitz空间上复合算子的有界性问题.
1 预备知识及相关引理
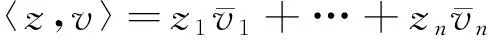
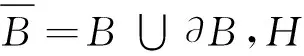
1)∀t>0,ω(t)单调上升;

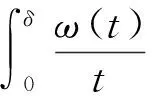

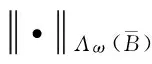
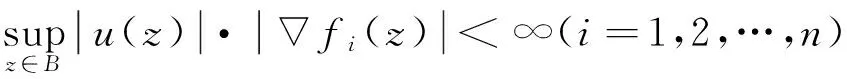
仿照文献[5]中的定理1和文献[6]中的定义4中的证明方法,得到如下命题.
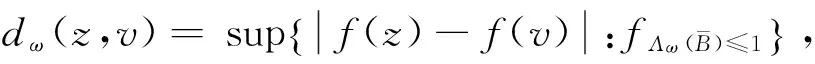
引理2设ω是一个权函数,f∈A(B),则
其中,“≈”表示等价号,在本文中,X≈Y表示存在一个常数C(ω)>0,使得C-1(ω)X≤T≤C(ω)X成立,这里的C(ω)是与权函数ω有关的常数.引理2由文献[1]引理6和定理1可知.
2 主要成果
文献[5]是关于加权复合算子在Cn中的Lipschitz空间上的有界性和紧性问题,但是一直未见有文献讨论Cn中的加权Lipschitz空间以及复合算子在此空间上的有界性问题.本文在此基础上通过空间中的诱导距离探究了Cn中加权Lipschitz空间的复合算子的有界性问题,得到了加权解析Lipschitz空间上的复合算子的有界性的充要条件:
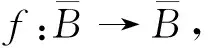
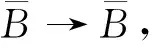
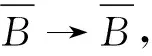
定理1设Cφ为加权Lipschitz空间上的复合算子,则下列条件是等价的:
(i)Cφ为有界算子;
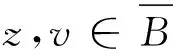
证明(i)⟹(ii).设Cφ有界,则
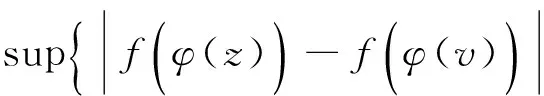
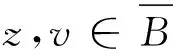
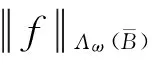
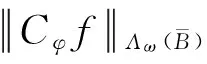
其中,
为φ在点z的导数.
证明设Cφ∶Cφf=f·φ有界,让φ=1,则Cφf=f∈Λω.再让φ=zi(i=1,…,n),则有Cφ∶Cφf=f·φi,故
(Cφf)(z)=(f·φi)(z)=φi(z)f(z)+f(z)φi(z)≤C.
又因f∈Λω,所以φi(z)f(z)≤C,从而∞.

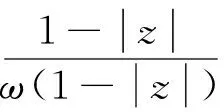

3 结束语
研究加权解析Lipschitz空间上复合算子的有界性和紧性有着实用性的意义,它被广泛的应用在动力系统中的各个应用领域.本文利用加权解析Lipschitz空间中的函数在Cn中的诱导距离给出了该空间上复合算子有界性的充要条件.
[1] DYAKONOV K M. Equivalent norms on lipschitz-type spaces of holomorphic functions[J]. Acta Mathematica, 1997,178(2):143-167.
[2] 戴济能.单位球上Lipschitz空间及其空间上的加权复合算子[J].武汉大学学报(理学版),2012,58(2):95-99.
[3] JINENG D A I, OUYANG C. Composition operators between Bloch type spaces in the unit ball[J]. Acta Mathematica Scientia, 2014,34(1):73-81.
[4] BLASCO O.Operators on Weighted Bergman Spaces(0 [5] 罗罗.某些多复变函数全体函数上的复合算子和一类推广的Hankel算子[D].合肥:中国科技大学,1998. [6] 任全玉,黄玲娣.加权解析Lipschitz空间的复合算子[J].河南师范大学学报(自然科学版),2006,34(1):136-138. TheBoundednessofCompositionOperatorontheWeightedLipschitzSpaceinCn ZHANG Yanlin, XIAO Jianbin, GAO Zhijuan (SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China) On the unit disc, the boundedness and compactness of the composition operator in the weighted Lipschitz spaces have been investigated, besides the necessary and sufficient conditions of the composition operatorCφare obtained. However, there is no discussion about the boundedness of the composition operator on weighted analytic Lipschitz spaces inCn. by describing the properties of weighted analytic Lipschitz space inCn, and combine with the properties of the induced distances in Lipschitz space, the necessary and sufficient conditions of the composition operatorCφin weighted analytic Lipschitz space are obtained. unit ball; weighted Lipschitz space; composition operator; boundedness O177.2 A 1001-9146(2017)05-0100-03 10.13954/j.cnki.hdu.2017.05.019 2016-12-01 国家自然科学基金资助项目(11571104) 张彦林(1988-),女,甘肃武威人,硕士研究生,复分析及其应用.通信作者:肖建斌教授,E-mail:xjb@hdu.edu.cn.
