集成现场标定功能的MEMS加速度传感器

吴迪东，董林玺

(杭州电子科技大学电子信息学院，浙江 杭州 310018)

集成现场标定功能的MEMS加速度传感器

吴迪东，董林玺

(杭州电子科技大学电子信息学院，浙江 杭州 310018)

针对传统机械振动台标定MEMS加速度传感器设备比较复杂且不方便现场标定的情况，设计了一种集成现场标定功能的加速度传感器.采用电磁驱动原理，用通电导线上产生的安培力模拟传统机械振动台惯性力.给出了加速度传感器结构，用有限元仿真软件ANSYS分析了传感器的运动模态和灵敏度，实现了弹性系数以及标定特性的验证.结果表明，所设计的加速度传感器谐振频率为1 528.84 Hz，静态位移灵敏度为0.109 μm/g.该传感器驱动力矩较大，线性好，同时可实现现场传感器性能标定，具有较好的应用潜力.

微机电系统；自标定；电容式传感器；电磁驱动

0 引 言

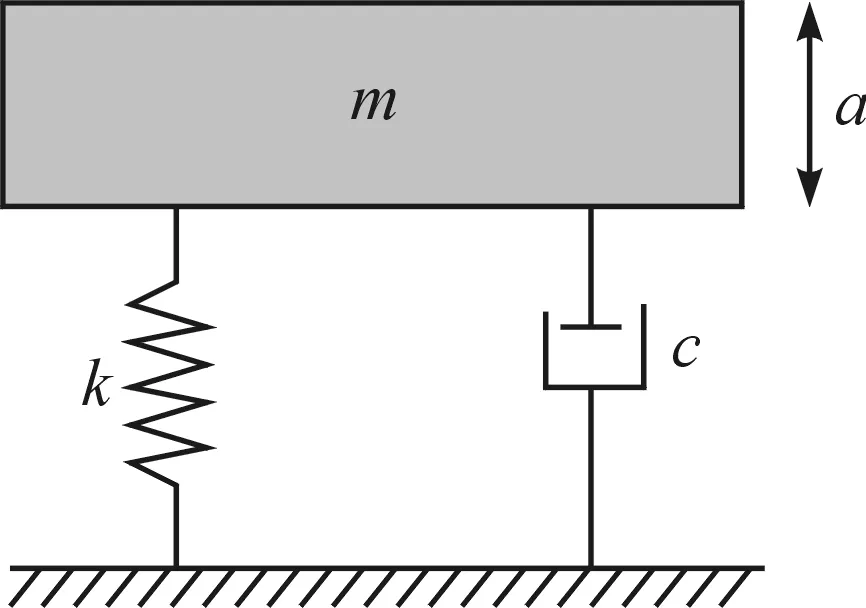
图1 加速度传感器的基本数学模型

微机电系统(Micro-Electro-Mechanical System，MEMS)电容式加速度传感器因温度系数小、灵敏度高等众多优良特性被广泛使用于汽车电子、工程测振等领域.而标定环节对于加速度传感器的准确应用显得至关重要.传统加速度传感器标定方法是机械振动台标定法[1]，即将待标定传感器与参照传感器背靠背绑在一起振动得到相关数据.显而易见，传统标定法虽然精准，但是比较复杂，设备昂贵，更不利于现场标定.为了解决这个问题，研究者提出了许多测试和标定方法，如内建自测试(Built-in self test，BIST)能简单地测试加速度传感器的好坏[2]，基于统计模型能预测三轴加速度传感器的参数[3].文献[4]提出了一种无需物理加速度激励的标定方法，采用静电力驱动代替物理加速度，以实现加速度计自标定.文献[5-6]基于压电特性的多轴微型标定振动台，实现了惯性传感器的现场标定，虽然在小尺寸上实现了真实振动加速度的产生，但是传感器在微小振动台上难以固定，且固定误差较大.此前，文献[7]对静电力标定MEMS加速度传感器做了相关工作，文献[8-9]也对静电力标定MEMS加速度传感器过程中电容边缘效应以及倾斜梳齿的影响进行过相关分析，然而这两者采用的静电驱动方式存在着非线性和驱动力矩小的问题，为此，本文采用电磁驱动方式设计了集成现场标定功能的MEMS加速度传感器.现场标定时，在锚点处电极施加驱动电流，质量块在安培力作用下正弦振动，其中驱动导线所处的均匀磁场由传感器顶部封装的永磁体提供.传感器经过出厂时的振动台校准，能在后续使用过程中实现准确的现场标定.

1 加速度传感器模型

在常规的传感器分析中，可用质量-弹簧-阻尼系统来近似表示MEMS加速度传感器的基本力学模型[10]，系统原理图如图1所示.

加速度a使敏感质量块产生位移x，其数学表达式为：

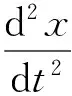
(1)

式中，m为质量块质量，k为弹性系数，c为阻尼系数.

2 电磁驱动的结构设计和标定原理

由于梳栅结构检测电容的特点介于梳齿结构和栅型结构之间，适合制作兼顾分辨率和灵敏度的传感器[11]，因此，本文采用梳栅结构检测电容.传感器结构如图2所示.

1—固定锚点;2—U型弹性梁;3—梳型电容;4—栅型电容;5—均匀磁场;6—固定通电导线;7—敏感质量块;8—连接电极和驱动导线的引线;9—质量块焊点;10—叉指铝电极对;11—梳齿检测电容的焊点;12—固定检测电极焊点;13—玻璃衬底.图2 传感器结构示意图

MEMS加速度传感器沿图2(a)中AA1的剖面如图3所示.图3中，最上层为通电导线所处的金属导线层，绝缘层位于其正下方，中间为硅体层，包括传感器的可动结构，最下层为玻璃衬底，叉指铝电极对位于玻璃衬底上.硅体和玻璃衬底通过硅-玻璃键合工艺键合.传感器三维结构如图4所示.外围4个梳型结构为固定梳齿检测电容，中间带有栅型结构的部分为弹性梁和敏感质量块，质量块上方附着金属导线，箭头为均匀磁场.

图3 自标定加速度传感器沿AA1剖面图

加速度传感器置于磁场之中，图2中5表示方向垂直纸面向内的均匀磁场B.传感器上铺设有金属导线.用外部金丝球焊技术将驱动导线和金属引线通过引出电极连接到封装管壳引脚上.以图2中箭头所示电流I为例，根据左手定则，通电导线受到竖直向下的安培力FB=BIL，使质量块产生向下的位移，其中L为通电导线长度.通电导线受力示意图如图5所示.由于传感器结构的对称性，驱动导线对受到的安培力相互叠加，而引线受到的安培力相互抵消，因此敏感质量块不会在标定时产生扭转，该结构是稳定的.

图4 传感器三维立体图

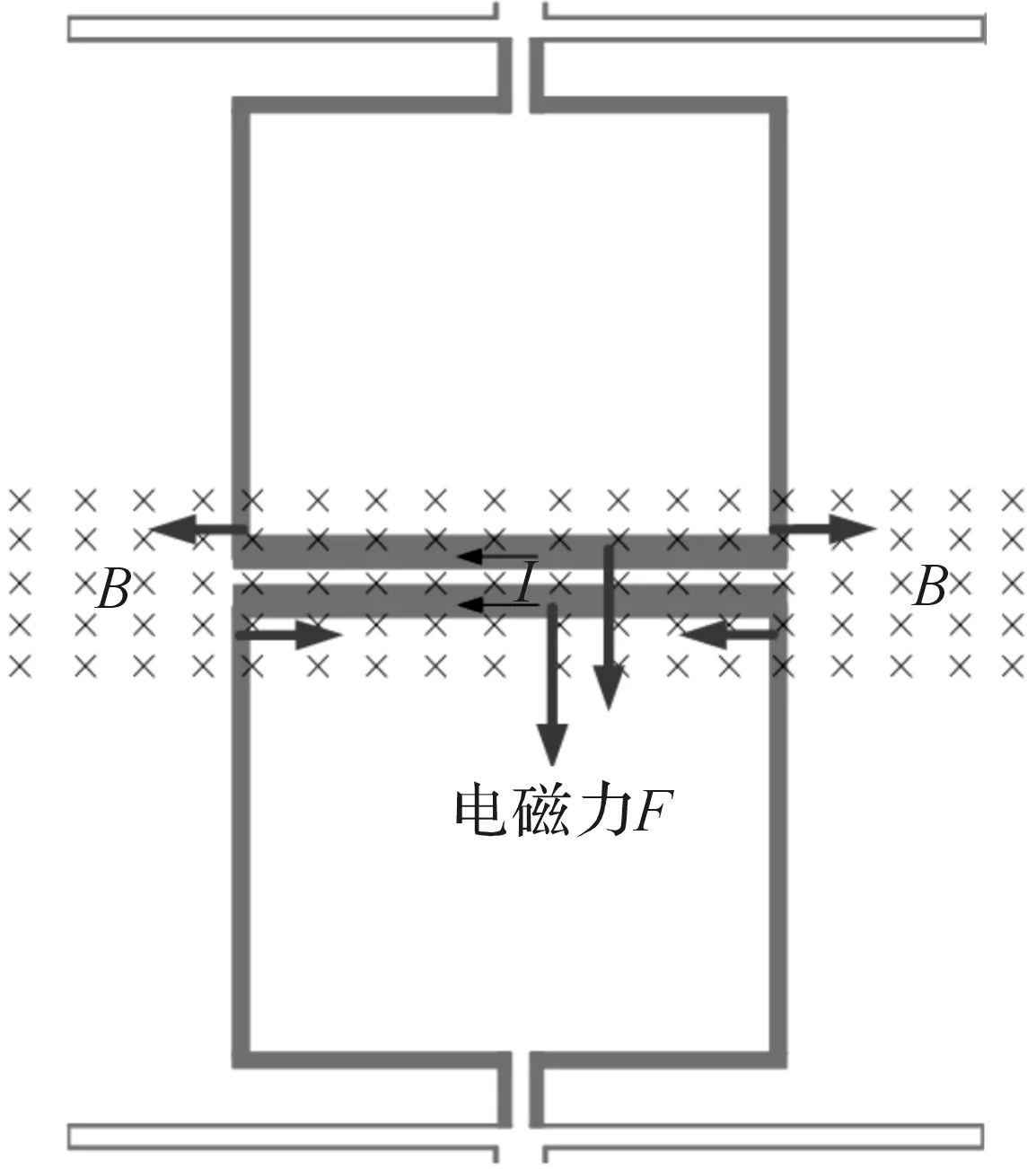
图5 通电导线受力示意图

本文设计的加速度传感器的部分参数如表1所示.

表1 加速度传感器部分参数

由于采用通电导线受到的安培力模拟外部加速度引起的惯性力，式(1)变为：

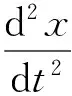
(2)

标定的目的是使敏感质量块呈正弦振动，假设正弦振动的曲线为：

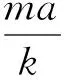
(3)

k为弹性系数，根据卡氏第二定理，可以推导出图2所示传感器结构的弹性系数公式为k=2Eb3t/l3.其中，E为杨氏模量，b为梁宽度，t为梁厚度，l为梁长度，ω为正弦振动的角速度.根据微积分基本知识，有

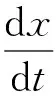
(4)

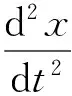
(5)

通电导线运动时，由于有效面积会改变，而磁感应强度B保持不变，因此磁通量会发生变化，根据法拉第电磁感应定律可知，通电导线产生感应电动势，形成感应电流，且总是沿着阻碍磁通量变化的方向.因此需要考虑感应电流对标定的影响，通电导线实际受到的力变为：

(6)

其中，v为磁场中导线切割磁感线的速度，R为闭合电路的等效电阻，i(t)为驱动电流.将式(4)—(6)代入式(2)，得到：

(7)

由于阻尼系数随着振动产生变化，为设计简便，忽略空气阻尼作用时，式(7)变为：

(8)

i(t)即为电磁驱动标定加速度传感器驱动电流.通电导线上电流方向改变时，敏感质量块受到的安培力也会相应地改变方向，从而使质量块相对平衡位置作正弦振动，达到自标定的目的.

当加速度传感器长时间工作后，由于环境变化、误差累积等因素使加速度传感器的准确性受到一定程度的影响，此时就需要重新对加速度传感器进行再标定.而消费者往往缺少机械振动台等昂贵的设备，且焊接到PCB板上的加速度传感器拆下进行再标定也不现实，因此以往普通的加速度传感器不能很好地应对此情形.本文设计的MEMS电容式加速度传感器能方便地解决此种问题，在需要再标定时，只需在电极处施加相应电流即可快速实现现场的标定.

然而由于工艺条件限制，实际加速度传感器成品在质量m、导线长度L、弹性系数k等参数上不可避免地存在误差，因此需要修正其对标定电流模拟真实加速度的影响.主要通过在传感器出厂前用机械振动台确定工艺误差修正因子的方法解决.大致的流程如图6所示.

图6 工艺误差修正流程

3 传感器性能分析

在设计微机械器件时，由于流片成本很高，常采用有限元软件进行模拟仿真.本文用有限元软件ANSYS对传感器结构进行建模分析.为了验证弹性系数公式的准确性，分别改变弹性梁长度和宽度，得到相应的理论值和有限元仿真值，绘制曲线如图7所示.结果显示，弹性系数随着梁长度增大而减小，随着梁宽度增大而增大，仿真结果符合理论值，验证了其准确性.

图7 弹性系数k仿真结果

在众多分析中，模态分析是基础分析，通过结构的频率、阻尼和模态振型等动力学属性判断设计结构的合理性.经过仿真，得到传感器的前四阶模态频率分别为1 528.84 Hz，11 246.52 Hz，12 255.11 Hz，21 454.22 Hz.其中一阶模态如图8(a)所示，此模态为传感器主模态，谐振频率最小，对加速度信号最为敏感，传感器的工作频率应小于此频率.

灵敏度是加速度传感器重要的静态特性，是指传感器工作状态稳定时(静态或频率很低)输入和输出的对应关系.对于电容式加速度传感器，位移灵敏度为位移和加速度的比值，即为S=Δx/a.当给传感器施加敏感方向的大小为1 g的加速度信号，其位移量如图8(b)所示，敏感质量块相对于平衡位置产生了0.109 μm的偏移量，因此本文设计的加速度传感器静态位移灵敏度S为0.109 μm/g.

图8 传感器静态特性

传感器的自标定响应曲线如图9所示.设定均匀磁场强度为0.06 T，传感器工作频率500 Hz，回路电阻为1 000 Ω，自标定幅值为1 g.根据输入电流得到质量块位移，方形实线代表质量块相对平衡位置的位移，星形虚线代表输入的自标定电流.位移峰值为0.109 μm，电流峰值为0.192 A.进一步分析感应电流对自标定的影响，以1/8周期为例，此时自标定电流为0.136 A，而感应电流仅为2.034×10-11A，感应电流远小于标定电流，因此可以忽略电磁感应产生的影响.

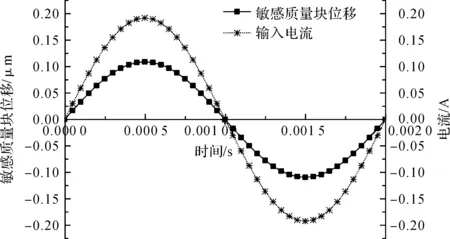
图9 传感器动态标定特性曲线

4 结束语

本文针对机械振动台标定方法不利于现场标定的问题，设计了一种集成电磁驱动标定功能的MEMS加速度传感器.采用通电导线安培力代替外界加速度，实现了用电流驱动的方式达到机械振动台同等效果.与研究较多的静电驱动方式相比，其电磁驱动力矩较大，并且避免了非线性.传感器产品携带方便，并通过了振动台校准，解决了消费者因缺少设备而不能现场标定的问题.下一步主要研究空气阻尼效应对于传感器标定的影响，使设计的传感器更好地契合实际工作情况.

[1] 陈传俊,陈志高.基于振动台的加速度传感器灵敏度的标定[J].大地测量与地球动力学,2013(z1):168-171.

[2] KOLPEKWAR A, BLANTON R D. Development of a MEMS testing methodology[J]. 1997:923-931.

[3] 林生荣,张辉.三轴加速度传感器校正方法研究[J].传感器与微系统,2011,30(11):72-74.

[4] DAR T, SURYANARAYANAN K, GEISBERGER A. No Physical Stimulus Testing and Calibration for MEMS Accelerometer[J]. Journal of Microelectromechanical Systems, 2014,23(4):811-818.

[5] NADIG S, ARDANUÇ S, LAL A. Monolithic piezoelectric in-plane motion stage with low cross-axis-coupling[C]//IEEE, International Conference on MICRO Electro Mechanical Systems. IEEE, 2014:524-527.

[6] AKTAKKA E E, NAJAFI K. A six-axis micro platform for in situ calibration of MEMS inertial sensors[C]//IEEE, International Conference on MICRO Electro Mechanical Systems. IEEE, 2016:243-246.

[7] DENG L, KUNDUR V, NAGA N S J, et al. Electrical calibration of spring-mass MEMS capacitive accelerometers[C]//Design, Automation & Test in Europe Conference & Exhibition(DATE), 2013. IEEE, 2013:571-574.

[8] DONG L, PAN Y, LOU J, et al. Study of the influence of fringe edge on MEMS capacitive accelerometers self-calibration[J]. Microsystem Technologies, 2015,21(6):1179-1186.

[9] 董林玺,楼进峰.倾斜梳齿的MEMS电容式加速度传感器自我标定特性研究[J].传感技术学报,2013(10):1357-1363.

[10] NAGA J, SAI N. Calibration of MEMS capacitive accelerometers using Electrical Stimulus BIST[J]. Dissertations & Theses-Gradworks, 2014.

[11] 董林玺,李寿洛,陈金丹,等.不同检测电容结构对MEMS电容传感器性能的影响分析[J].传感技术学报,2010,23(4):501-507.

AMEMSAccelerationSensorwithFieldCalibrationFunction

WU Didong, DONG Linxi

(SchoolofElectronicInformation,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

With the problem that the traditional mechanical MEMS vibration table is complicated and inconvenient to calibrate on the spot, an accelerometer with integrated field calibration function is designed. The principle of electromagnetic drive is used to simulate the inertia force of traditional mechanical vibration table. The structure of the accelerometer is given. The motion mode and sensitivity of the sensor are analyzed with the finite element simulation software ANSYS, and the elasticity and calibration characteristics are verified. The elastic coefficient and the calibration characteristics are verified. The results show that the resonant frequency of the designed accelerometer is 1 528.84 Hz and the static displacement sensitivity is 0.109 μm/g. The sensor has high driving torque and good linearity. At the same time, it can realize the on-site performance calibration, which has good application potential.

MEMS; self-calibration; capacitive sensor; electromagnetic drive

TP212.1

A

1001-9146(2017)05-0012-05

2016-11-07

吴迪东(1991-)，男，浙江嵊州人，硕士研究生，传感器原理及其应用.通信作者：董林玺教授，E-mail:donglinxi@hdu.edu.cn.

10.13954/j.cnki.hdu.2017.05.003