改进TOPSIS法的装备可靠性评估方法

史金朋

(中国人民解放军93868部队，银川 750025)

改进TOPSIS法的装备可靠性评估方法

史金朋

(中国人民解放军93868部队，银川 750025)

装备的可靠性是完成遂行任务必备条件，对装备可靠性进行评估可为任务决策提供理论支持;目前关于装备可靠性评估方面的研究大多数都是基于概率统计学的，而概率统计的准确性受限于样本的大小，从而使得基于概率统计学的装备可靠性评估因装备样本的大小而产生不可避免的或大或小误差;为解决这一评估受样本大小制约的问题，引入逼近理想点(TOPSIS)法;同时，针对TOPSIS法受主观因素影响较大的问题，修定了该法评估指标权重及理想解的确定方法，并在评估结果中引入了“合格分数线”的概念，使得评估结果等级划分有了量化依据，从而体现出了客观性和科学性，然后构建了某装备基于该改进TOPSIS法的可靠性评估模型;最后，通过示例分析，利用MATLAB计算验证了本文方法的正确性，评估结果可为装备的使用者或指挥者提供决策依据。

装备评估；可靠性；TOPSIS法

0 引言

装备的可靠运行是完成既定目标任务的首要前提之一，评估装备可靠性对分析预想目标的可行性具有重要意义。然而，当前在用装备交融了多门学科、众多领域的知识结构，传统的“望闻问切”等方法已不能很好检测或评价其可靠性。

对此，已有部分研究取得了较好成绩，主要表现为基于概率统计学的装(设)备可靠性评估[1-5]，但这类方法的评估结果受装备样本数据影响较大。尤其在评估单一装备时，由于历史样本数据较少，此种可靠性评估方法评估结果将不可避免地产生较大误差。然而，基于概率统计学外的装备可靠性评估研究却很少见，如：文献[6]通过主客观打分建立了非线性指标聚合的评估方法，虽不受样本数据大小影响，但以主观“打分”为基础评估可靠性在一定程度上削减了客观性。本文引入并改进了逼近理想点(Technique for Order Preference by Similarity to Ideal Solution，以下统称TOPSIS)法，将评估对象置于所履行的目标任务当中，构建可靠性评估模型，并以评估指标的边界为依据在评估结果中计算“合格”标准，以此划分评估结果等级，以期为装备的使用者提供较为准确、客观的评估结果。

1 现代装备特性分析

在技术创新的有力驱动下，现代装备在宏观上呈现出学科属性交叉、知识领域交互、理论边界模糊等特点，更向着综合化、集成化、系统化的方向发展；在微观上则呈现出电子与机械融合、硬件与软件兼容等特点，更向着精细化、信息化、智能化的方向发展。这对装备的操作使用、维护保养、测试维修、安全可靠等方面都提出了新的研究课题。

就可靠性而言[7]，是指装备在规定的条件下和规定的时间内，完成规定功能(目标任务，以下简称任务)的能力。对装备可靠性的评估就是通过算法量化给出这种能力的大小，为装备指挥者提供决策依据。对具体装备来说，由于装备的复杂性和高整合性，使得其可采集到的能表征其可靠性的参数指标比较少，如何利用有限的数据准确评估装备的可靠性是这一研究领域的瓶颈问题。

2 TOPSIS法改进策略

TOPSIS法是于1981年提出的一种分析多目标、多属性问题的决策方法。

2.1 TOPSIS法基本思想

TOPSIS法的核心是构造正理想解和负理想解，以判断目标问题与正、负理想解的偏离程度来确定决策方案的优劣性。即当目标解越与正理想解近，且越与负理想解远时，则该目标解就越优。TOPSIS法基本流程[8]如图1所示。

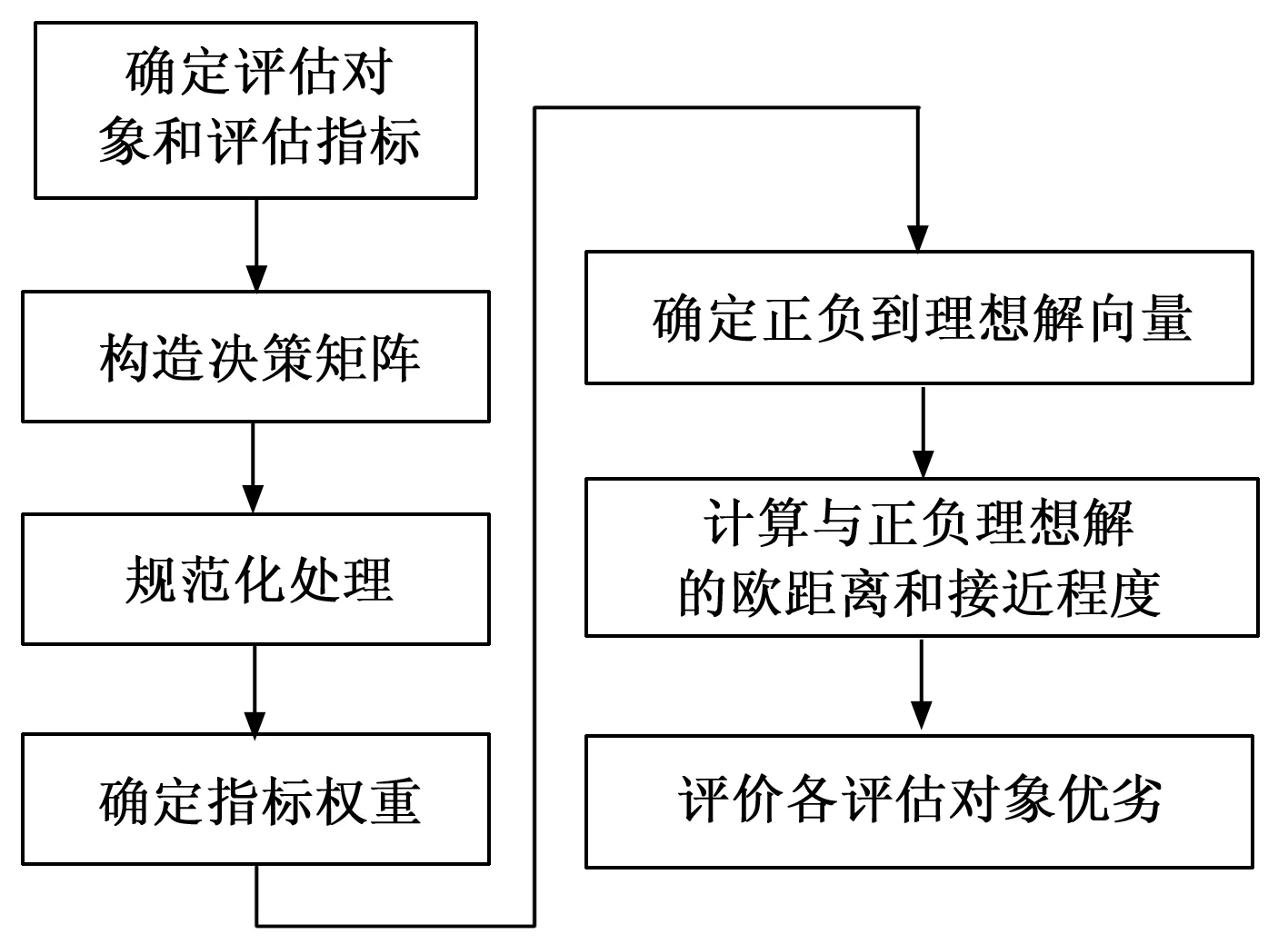
图1 TOPSIS法基本流程

图1中,设有m个评估对象，n个评估指标的决策矩阵为X=[xij]m×n，其中i=1,2,…,m，j=1,2,…,n。由式(1)进行规范化处理得到规范化决策矩阵Y=[yij]m×n，其中：

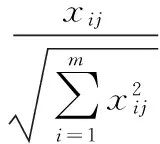
(1)

实际上，每个评估指标在评估体系中所占的比重不尽相同，即设对应指标权重为向量w=(w1,w2,…,wn)，其中w1+w2+…+wn=1，由此得到加权规范化决策矩阵Z=[zij]m×n，其中zij=wjyij。再设正理想解向量为Z+=(zj+)1×n，Z-=(zj-)1×n，其中：

(2)

需要说明的是：式(2)中max表示最优解，而不是最大值；min表示最劣解，并不是最小值。又设评估对象到正负理想解的距离分别为d+和d-，则:

(3)

(4)

评估对象与正理想解的相对接近程度用C表示，则:

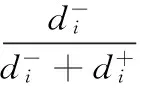
(5)

最终，评估对象的优劣顺序由C值确定，其值越大说明对应评估对象越优。

2.2 TOPSIS法分析

TOPSIS算法简单易掌握，便于计算，可信度较高，且不受评估对象样本大小、分布形态等方面的限制。但其受主观因素影响较大，使得评估结果可信度在一定程度上打了折扣，主要体现在：1)评估指标权重的选取；2)正、负理想解的确定。

原TOPSIS法的评估指标权重选取主要凭借经验判断或专家打分等主观方法，或大或小地削弱了评估结果的准确性。研究表明[9]：对于选取多方案决策类的评估可通过引入信息熵权通过指标变异程度的大小来解决这一问题，但本文是对装备可靠性的评估，不能单纯依指标变异程度来衡量其重要性。

原TOPSIS法的正、负理想解来源于评估对象样本数据的最值。一般情况下，样本数据的采集受测量者工作态度、精神状态及文化程度及评估对象本身属性等方面要素影响较大。由此确定理想解，用于特定装备可靠性评估时，会出现理想解“跑偏”的现象，从而会导致评估结果出现偏差。

2.3 TOPSIS法的改进

基于以上分析，本文改进主要针对评估指标权重和评估对象正负理想解的确定两个方面。

2.3.1 评估指标权重修定方法

考虑到装备的可靠性是针对其完成具体任务而言的，将评估指标权重与既定的任务相关联是合理的。这里区分装备的评估指标与任务之间的逻辑关系而施行不同的处理策略。评估指标与装备完成任务之间的逻辑关系(如图2所示)简化表征为“与”和“或”关系，若不是简单的与或关系可通过逻辑关系计算变换为与或关系。

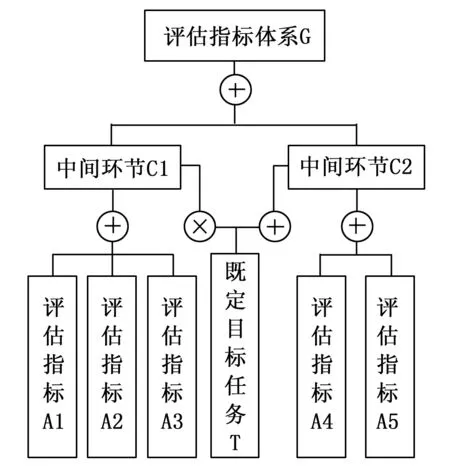
图2 装备评估指标与任务逻辑关系

图中，“⊕”表示逻辑或关系、“⊗”表示逻辑与关系。由图可见任务T分别与指标A1、A2、A3构成逻辑与关系，又分别与指标A4、A5构成逻辑或关系。注：在实际计算中，任务T只体现逻辑关系而不参与数值计算。

实际上：评估指标与目标任务逻辑“与”关系体现为“必须正常”，如果此类“与”指标出现异常则“一票否决”。因此，这此指标权重一律平等，不应区分大小，为计算方便设定权重为1；对于逻辑“或”关系，则指标权重不受目标任务限制，其权重有大小之分。为消减主观因素影响，这里采用信息熵权方法确定逻辑“或”的指标权重w°j[9]，即：

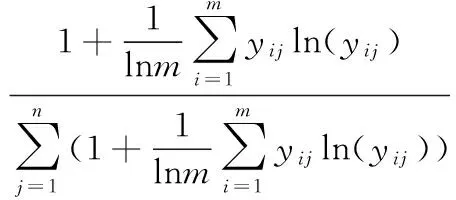
(6)

式中，yij为规范化矩阵元素。

最后，将所有权重进行归一化处理后，确定为最终权重向量。

2.3.2 评估对象理想解的确定

为避免如奇异值等非客观样本数据被选定为正、负理想解，本文将正理想解定义为对应评估指标的装备出厂或研制定型时的理论数据。对于没有此数据的指标，取该评估指标样本数据中最优的1/10样本平均值，如果样本不能被10整除则向下取整但不能少于1。负理想解的选取与原TOPSIS法相同。

3 某装备的可靠性评估模型

装备的可靠性评估是针对装备在完成某项既定目标任务而开展的预评价。评估指标应选取能表征装备健康状态的参数，且应以任务为依据，将能体现完成任务的参数也纳入评估指标体系。

某装备的基于改进后TOPSIS法的可靠性评估算法流程描述如下：

STEP1：确定评估装备对象、目标任务和评估指标，并构建决策矩阵；

STEP2：规范化处理决策矩阵，得到规范化决策矩阵；

STEP3：确定指标权重。首先分析梳理出各指标与目标任务的与或逻辑关系：“与”关系，确定对应指标权重为1；“或”关系，对应指标权重依式(6)计算。其次，所有指标权重确定后，进行归一化处理，使权重之和等于1。

STEP4：对STEP3中构成“与”关系指标首先进行评估，如果该指标当前数据超出临界值则一票否决：装备不可执行此任务。否则转STEP5。

STEP5：分别依据2.3.2节方法及式(2)确定正、负理想解向量。

STEP6：依式(3)和式(4)计算评估对象与正负理想解距离。注：对于单一装备，分别计算史上最优(出厂理论解)、临界值、当前数据与正负理想解的距离；对于多台同型装备，分别计算各台装备平均史上最优(出厂理论解)、临界值、各台装备当前数据与正负理想解的距离。其中，临界值是指装备某一指标数据的合格范围边界，当指标临界值的组合较多时应分别计算。

STEP6：依式(6)计算各接近程度。其中，当指标临界值的组合较多时，选取接近程度最大作为“合格分数线”值。

STEP7：输出评估结果。

装备可靠性评估结果分为优秀、良好、合格、不合格4个等级，其中合格线以计算各指标“临界值”的接近程度确定。所以，装备可靠性评估等级是一个动态过程：优秀、良好、合格区间边界在合格线确定后向最优方向三等分确定。装备评估结果如表1所示。

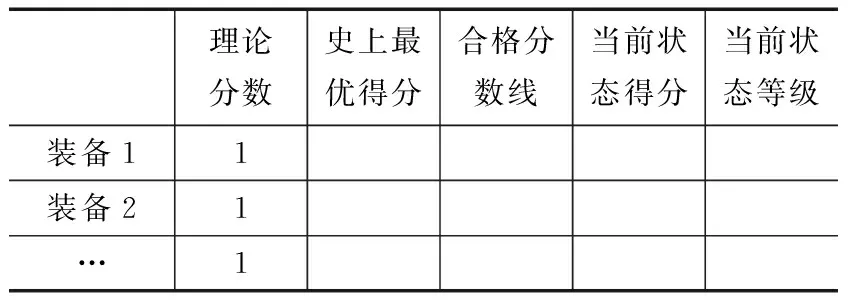
表1 装备可靠性评估结果

表1中：“理论分数”指装备在研制定型或出厂给出的理论指标数据下的接近程度，定义为1；“史上最优得分”是本装备历史最好时的指标数据下的接近程度；“合格分数线”是本装备各指标“临界值”下的接近程度；“当前状态等级”是根据本装备当下指标数据计算得出的评估结果等级。

4 示例分析

某装备的评估指标为：电阻1(允许范围为1.0～1.5 Ω)、电阻2(允许范围为0.6～1.0 Ω)、电压(允许范围为4～6 V)、振动频率。目标任务为正常使用。其中电阻1、电阻2、电压与其构成“与”关系，振动频率为“或”关系。为节省篇幅，经筛选后其基本样本数据如表2所示。

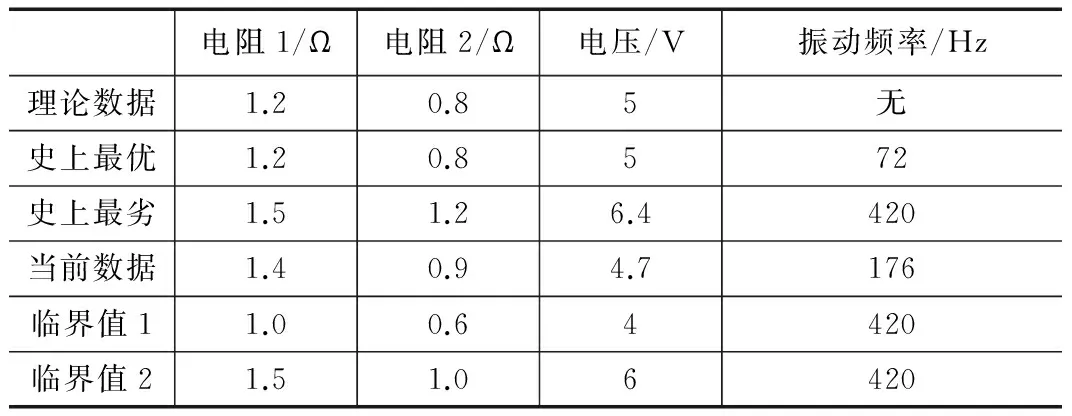
表2 某装备评估指标基本数据

取振动频率的“理论数据”为历史最好前10位平均值83 Hz。考虑到部分指标临界值关于理论数据对称，将临界值组合简化为两个，其中临界振动频率取史上最劣频率，则该装备的评估决策矩阵为：

利用Matlab7.1进行依本文第2和第3节内容计算，得：权重向量为(0.2848，0.2848，0.2848，0.1456)；选取的正、负理想解分别为(1.2，0.8，5，83)和“史上最劣值”对应的加权规范化决策矩阵值(0.1063，0.0800，0.1099，0.0160)和(0.1328，0.1200，0.1407，0.0809)；“史上最优”、“史上最劣”和“当前状态”、“临界值1”和“临界值2”接近程度分别为0.9765、0、0.7082、0.5540和0.2229。由于当前状态数据均在指标的允许区间内，不存在“一票否决”。即，该装备可靠性评估结果如表3所示。

表3 某装备可靠性评估结果

根据表3，可见0～0.554为不合格，0.554～0.703为合格，0.703～0.852为良好，0.852～1为优秀。根据当前状态得分可见该装备当前状态良好，可以完成既定目标任务。另外，根据表3还可以得出：该台装备基本上完成了研制定型的指标要求；状态虽处于良好，但接近合格，可能处于“亚健康”状态，需加强维护保养。以上结果与该装备实际情况相符。为防止采集到的当前指标数据异常，可依此方法通过最近多批次数据进行评估验证再得出结论。

5 结论

改进后的TOPSIS法，使装备评估指标权重更加客观、理想解的来源更加合理：权重的选取以装备所履行的目标任务为依据区分逻辑关系分别确定，这样将装备置于任务中进行评估更具科学性；理想解首选装备研制或出厂的理论数据更具“理想”性，同时克服了以最优“样本”为理想解的样本本身带来的误差。装备评估结果中引入“合格分数线”使评估结果等级不再是一个无量化依据的模糊量，使评估结果的可信度更高。

本文方法简单易懂，评估过程紧贴装备所担负目标任务等实际情况，评估不受装备评估指标样本大小影响，结果较准确可靠，既适合单一装备的可靠性评估也适用于多台装备的可靠性评估。

[1] 郭忠来，吴 华，胡永刚,等.基于数据深度的设备状态评估模型研究[J].系统工程与电子技术，2014，36(5):897-899.

[2] 宋 飞.多机协同条件下机载雷达的效能评估研究[D].郑州：郑州大学，2015:28-39.

[3] 严英杰，盛 戈，王 辉,等.基于高维随机矩阵大数据分析模型的输变电设备关键性能评估方法[J].中国电机工程学报，2016，36(2):435-445.

[4] 马庆跃.武器装备体系作战效能综合评估技术研究[J].哈尔滨工业大学，2015:7-20.

[5] 何 迪，章 禹，郭创新.一种面向风险评估的输电线路故障概率模型[J].电力系统保护与控制，2017，45(7):69-75.

[6] 王义冬，刘 义，石伟峰.基于作战效能的武器装备可靠性指标评估方法[J].现代防御技术，2011，39(5):166-170.

[7] 贾治宇.武器装备通用特性指标体系研究[A].大型飞机关键技术高层论坛及中国航空学会2007年学术年会论文集[C].2007:1-5.

[8] 胡元潮，阮江军，杜志叶.基于TOPSIS法的变电站一次设备智能化评估[J].电力自动化设备，2012，32(12):22-27.

[9] 党兴华，李全升.基于熵权改进TOPSIS的陕西国家级高新区创新发展能力评价[J].科技管理研究，2017，3:75-83.

A Reliability Evaluation Method of Equipment on Improved TOPSIS

Shi Jinpeng

(No.93868 Unit of PLA, Yinchuan 750025, China)

The reliability of equipment was necessary to carry out the task conditions, equipment evaluation could provide theoretical support for the decision task.Most reliability research of equipment evaluation was on probability statistics, however, the accuracy of probability and statistics was limited by the size of the sample, so that the reliability evaluation based on probability and statistics was inevitable which was either largly or smally. In order to solve the problem that the evaluation was restricted by sample size, the method of TOPSIS was introduced. At the same time, aiming at the problem that TOPSIS method was influenced by subjective factors, the ascertained method of evaluation index weight and ideal answers on the TOPSIS were improved, and the evaluation model of equipment reliability based on this improved TOPSIS was build.This paper get rid of the restraint of sample capacity,and also the concept “qualified point line” was introduced into the evaluation result, so that the classification of the evaluation results had a quantitative basis, which reflected the objectivity and scientific. Lastly, the method on this paper was checked to be correct by the example and MATLAB,The evaluation results could provide the decision basis for the user or the commander of the equipment.

equipment evaluation; reliability; TOPSIS

2017-04-18；

2017-05-09。

史金朋(1986-)，男，河北广平人，技师，主要从事装备评估方向的研究。

1671-4598(2017)08-0300-04

10.16526/j.cnki.11-4762/tp.2017.08.077

TP302.7

A