条干均匀度仪波谱图算法设计与实现

李 征, 马建伟

(河南科技大学 信息工程学院，河南 洛阳 471000)

条干均匀度仪波谱图算法设计与实现

李 征, 马建伟

(河南科技大学 信息工程学院，河南 洛阳 471000)

条干均匀度仪的波谱图能够精确地反映出纱疵的周期性特征，从而可以快速地确定出纺纱工艺流程中故障的位置;但是如何将波谱图快速准确地实现一直是研究的难点;基于数字信号处理中的重采样定理，通过对不同机械故障所产生的纱线信号进行分析，改进了条干均匀度仪波谱图算法，该算法在需要观测的波长范围内构建了110个不同频带的带通滤波器，根据相邻滤波器频带关系分组进行波谱分析;通过DSP28335微处理器的数据采集、信号处理和上位机波谱图显示的系统进行实验，结果证明了该算法的可行性；其改进后的算法极大地减小了以往所用硬件的复杂度、提高了运算速度并拓宽了波谱图的可观测范围，且能够更精确的检测出故障位置。

波谱图；机械故障；带通滤波器

0 引言

随着人们对衣物舒适度要求的不断提高，减少纱疵成为纺纱企业的核心任务。纱线的波谱分析是减少纱疵，提高纱线质量，增加企业利润的最直接有效的方式。纱线的波谱图是通过纱线信号经过多组通带不同的带通滤波器产生的。滤波器的数目越多，滤波效果越好，分析得到的结果越精确。在不影响系统实时性的情况下，如何获得更精确的结果是实现波谱图设计面临的最主要问题。

目前，国内条干均匀度仪厂家技术相对落后，大多是通过使用模拟元件搭建多个带通滤波器对纱线传感器信号进行滤波完成的[1]。国内条干均匀度仪市场基本被国外厂家垄断。采用模拟电路实现，电路结构异常复杂，同时电路的可靠性和准确性都大大降低。一旦出现故障，维修耗时耗力。伴随着嵌入式技术大量地被运用于工业生产中，使用微控制器实现波谱图成为了历史的必然。但如果不进行任何算法优化，单纯地采用数字滤波器方式来单独实现每一个滤波器，则滤波器计算会耗费大量的CPU资源。势必使系统的实时性极大地减弱，导致其他功能无法正常实现。

本文通过对不同工艺故障产生的纱线信号进行分析，得到纱线信号的数学模型。基于数字信号处理中的重采样定理，提出了一种滤波器分组优化算法。在此基础上，搭建了以DSP28335为核心控制器的数据采集，信号处理和上位机波谱图显示系统。该算法的提出不仅解决了硬件电路复杂和软件实时性差的问题，同时还提高了波谱图显示的精度，能够更加准确地定位出纺纱过程中产生故障的机械设备位置。通过大量重复试验，产生的波谱图与行业标准乌斯特条干均匀度仪波谱图相比较，波形轮廓和对应幅值基本一致，证明了该系统的准确性和稳定性。

1 纱线信号数学模型

在纺纱过程中，由于纱线需要经过多种工艺设备，任何一种工艺设备异常都会在纱线上形成纱疵。把所有工序中可能形成纱疵部位的波长计算出来，与波谱图中异常波长相对比，即可快速确定故障的具体位置，便于工人维修。常见的部分可形成纱疵部位的波长见表1。

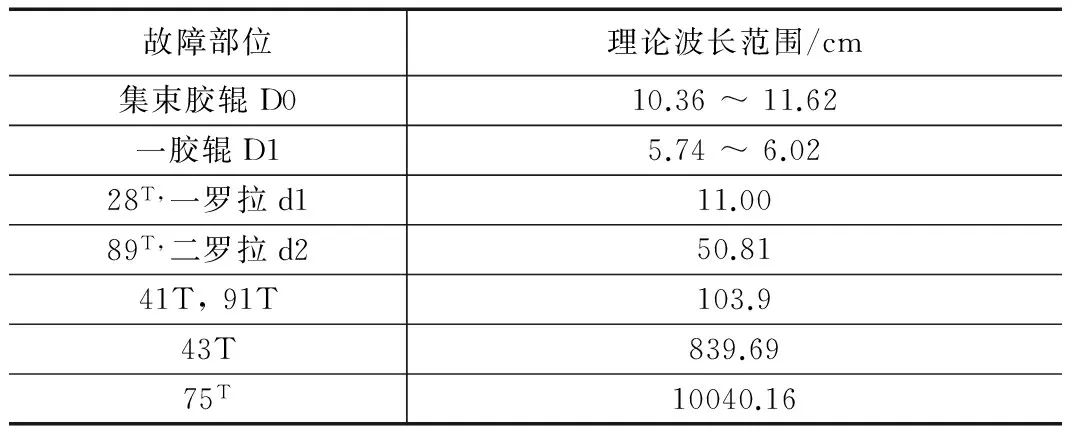
表1 常见故障部位波长

待检测的纱线信号可等效为无限带宽、幅值在有限范围内随机波动的数字信号叠加而成，如图1所示。设t时刻纱线信号的幅值为At，频率为f的纱线信号幅值为Aft，则纱线信号可表示为：

(1)

从表1我们可以得到，常见部位纱疵的波长在5.74 ～10 040.16 cm之间，若纱线的速度为1 000 m/min，则频率范围在292.43～ 0.166 Hz内。总的频率范围为300 Hz。理论上纱线信号的频率范围为0～+∞ Hz，波长范围为0～ m。实际处理时将其看作有限范围幅值、有限频率的数字信号进行处理。考虑到系统的采样频率fs是固定值，如果直接对采样的数据进行处理，那么高于fs/2的频率分量被当作低于fs/2的分量再次出现在频谱中，破坏了低于fs/2的频谱分量的完整性。为减少数据分析误差，采取了数据压缩算法和抗混叠滤波处理。由于CPU频率的限制，不可能对每一微小片段纱线直径信号都进行采样，因此采取1 cm采样一个点的方式来采集。若纱线速度为V/(m/min)，则采样频率:

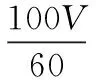
(2)

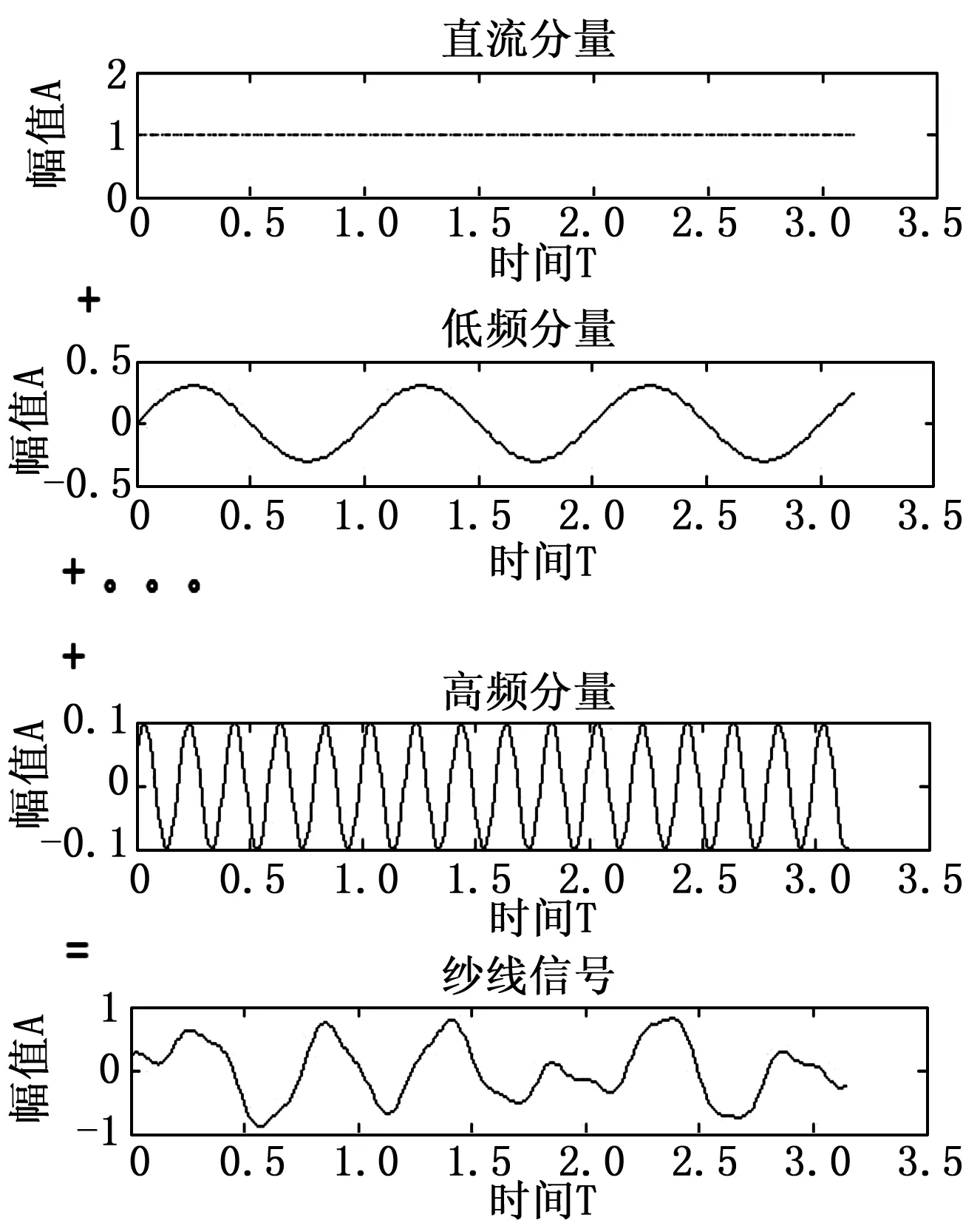
图1 纱线信号的叠加

2 滤波器分组优化算法

通过分析可以得到每隔10个频段，相应的频率带宽正好变化一倍。根据数字信号处理中的重采样定理可知，在其他参数不变的情况下，采样频率升高为原来的两倍，则滤波器的滤波频率也会变为原来的两倍，总带宽也变为原来的两倍。由此可将110个带通滤波器分为11组，最高频率的10个带通滤波器为一组，下一组滤波器的频率为上一组滤波器频率的一半。由此可知，只需设计出频段最高一组的10个滤波器，然后依次对采样数据进行1/2重抽样再通过这10个滤波器中，即可相当于实现110个带通滤波器。算法结构如图2所示。

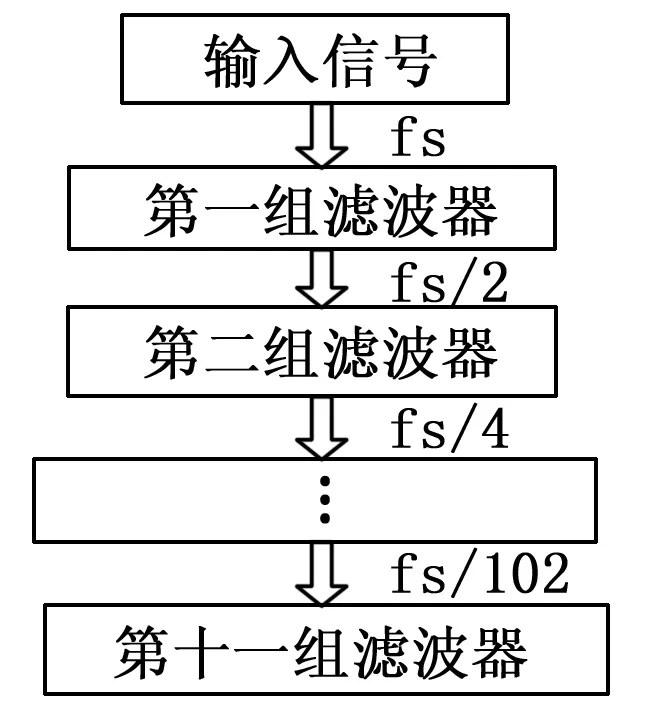
图2 滤波器分组优化算法

若不加任何优化算法实现，则需要首先设计110个频带不同、频带窄且精度高的带通滤波器。若采样数目为N，每个采样点都需要经过110个带通滤波器，则计算次数为110*N次。若采用分组优化算法，则只需要设计出频率最高的十个带通滤波器，大大减少了滤波器的数目，降低了实现的难度。第一次N个采样点通过这10个带通滤波器，第二次N/2个采样点再次通过这10个带通滤波器。以此类推，计算次数为：20N(1-1/211)。经过分组优化算法后，系统的运算量仅为常规算法的18.17%，极大地提高了DSP的效率。

3 硬件系统设计

整个系统的工作流程为：通过电容式传感器检测纱线直径的变化，输出的电压模拟量通过抗混叠滤波电路输入到DSP28335中。DSP对采集到的数据进行数据压缩处理后，按照分组优化算法进行滤波处理，同时DSP将处理后得到的数据经过RS485总线传输到上位机进行显示。系统原理如图3所示。

图3 系统原理框图

系统采用电容式传感器来检测纱线信号，信号幅值的波动代表了纱线直径的改变。由于纱线直径变化很小，系统实时性要求也很高，所以对选用的电容式传感器灵敏度和动态响应要求很高，必须能够检测出微小的电容变化量。经综合考虑，电容传感器选择Acam公司的PCap01。PCap01芯片内部带有内部接地补偿和外部漂移寄生电容补偿的单片机处理单元，完美地融合了高精度测量，低功耗测量以及快速测量的优点[2]。测量频率高达500 kHz，同时具有超高的温度稳定性，超低温漂，每摄氏度温漂仅为30 af。性能特点完全符合该系统的要求。PCap01芯片支持单一接地模式、单一传感器漂移模式、差分传感器接地模式、差分传感器漂移模式等连接方式[3]。本次实验采用差分传感器接地模式。

纱线信号经过低通滤波器(抗混叠滤波器)滤除超过900 Hz以上的高频部分，避免发生信号混叠现象。如果不使用抗混叠滤波电路，会在信号频带内产生位于期望频带之外的噪声信号。抗混叠减弱了大于采样频率fs/2以上的全部噪声频谱。低通滤波器由模拟运放组成，该电路同时把电压调整到合适的范围以便输入AD转换芯片。为了把放大器对检测单元的影响降到最低，在对信号进行放大之前，首先选用了由集成运放构成的跟随器对电路进行了隔离处理。运算放大器选用了具有更高输入阻抗、具有极低输入电流和高速性的ADTL084ARZ。由集成运算放大器组成的放大电路相比于差分放大电路和晶体管放大电路具有以下优点：1)硬件电路简单明了，元器件少，减小了电路板的面积；2)放大倍数和共模抑制比好，温漂小；3)集成度高，可靠性好；4)价格低廉，易于购买。由集成运放组成的信号调理电路如图4所示。

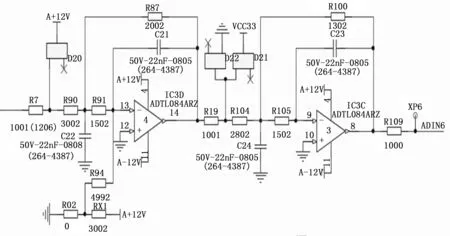
图4 信号调理电路

A/D转换采用的是TI公司的ADS7871。ADS7871是一款精密可编程的、14位逐次逼近式的模数转换器。为提高系统的电磁兼容性能，A/D输出部分需要外加隔离电路。DSP在该系统中处于核心地位，不仅仅需要设计带通滤波器和波谱分析同时还需要和上位机通信。在数据通信中，常用的方式有RS485总线、工业以太网和can总线等。综合考虑后，选用了硬件电路简单、传输速度快、实时性好的RS485通讯。

所设计的RS485通讯电路采用的芯片是SN65HVD08。SNH65HVD08结合了三态差分内联驱动器和差分线路接收器，用于和ANSITIA/EIA-485-A和ISO-8482E标准的设备进行互操作。该芯片的工作电压范围为3～5.5 V。可采用与DSP28335相同的电压3.3 V。减少电源电路的复杂性。

DSP通过RS485总线方式把数据传递给上位机进行实时显示。上位机程序采用的是基于.NET Framework的高级程序设计语言C#。C#比其他语言更适合现代开发工具，同时具有Visual Basic语言的易用性和C++的高性能、低内存访问。系统核心控制器采用的是TI公司的TMS320F28335，该芯片是一款32位的浮点型DSP，工作频率为150 MHz，具有独立的硬件乘法器，指令以流水线方式运行，运算速度很快[4]。并且DSP28335在逻辑上有4M*16位的程序空间和4M*16位的数据空间，可以缓存大量的监测数据。DSP28335具有很强的数字处理能力，完全满足该系统的实时性要求。

4 软件系统设计

利用TI官方的软件开发工具CCS6.1.3来进行系统软件开发。CCS6.1.3是官方推出的最新包含在线调试功能的开发工具，极大地方便了程序的编写和调试。采样部分采用数据压缩算法。A/D采用通过DSP28335的定时器中断中完成。采样频率为10 K，利用采样压缩算法将采样频率压缩至2 K。采样压缩流程如图5所示。

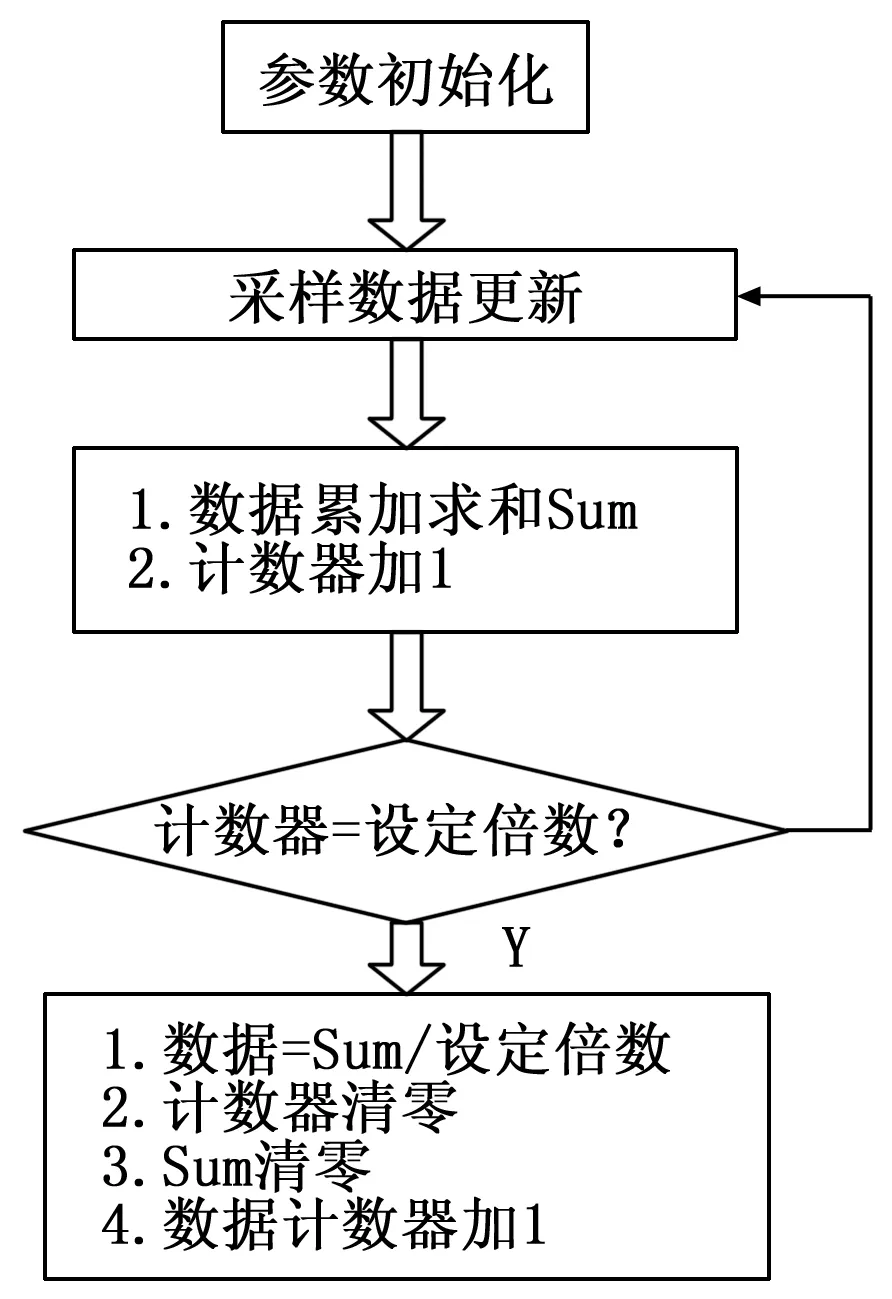
图5 采样压缩流程图

利用MATLAB软件的FDATool模块来设计第一组滤波器。数字滤波器可以分为IIR和FIR两种[5-6]，IIR数字滤波器适用于待分析数据量大，实时性要求高，对边缘频率要求精确的场合。FIR滤波器适用于待分析数据量小，实时性要求不高，对相位要求高的场合[7]。系统由于主要分析波长和纱线直径信号的幅频关系，对相位不做特殊要求，边缘频率要求高，实时性好，综合分析后采用IIR数字类型滤波器。Chebyshev型滤波器在通带内呈等波纹振荡，阻带内单调下降并且适用于数据量大的场合[8]。Butterworth滤波器阻带衰减不均匀，适用于待处理数据量略小的场合。为保证系统的实时性和可靠性，最终选用IIR型的Chebyshev滤波器。

IIR从结构上可以分为直接I型、直接II型、级联型和并联型4种[9]。现在常用的是级联型，主要优点是存储单元少，硬件结构简单，计算量小。具体级联结构如式：

(3)

根据滤波器设计原则：设计的滤波器的最小衰减倍数必须大于A/D所能表示的最小信号。故设计的滤波器最小衰减αs为-78 dB，通带允许的最大衰减αp为0.1 dB。若设置纱线速度为1 000 m/min，通过压缩采样算法后数据采样频率设置为1 000 Hz，滤波器的阶数设置为四阶。则设计出的第一个滤波器的幅频响应曲线如图6所示。

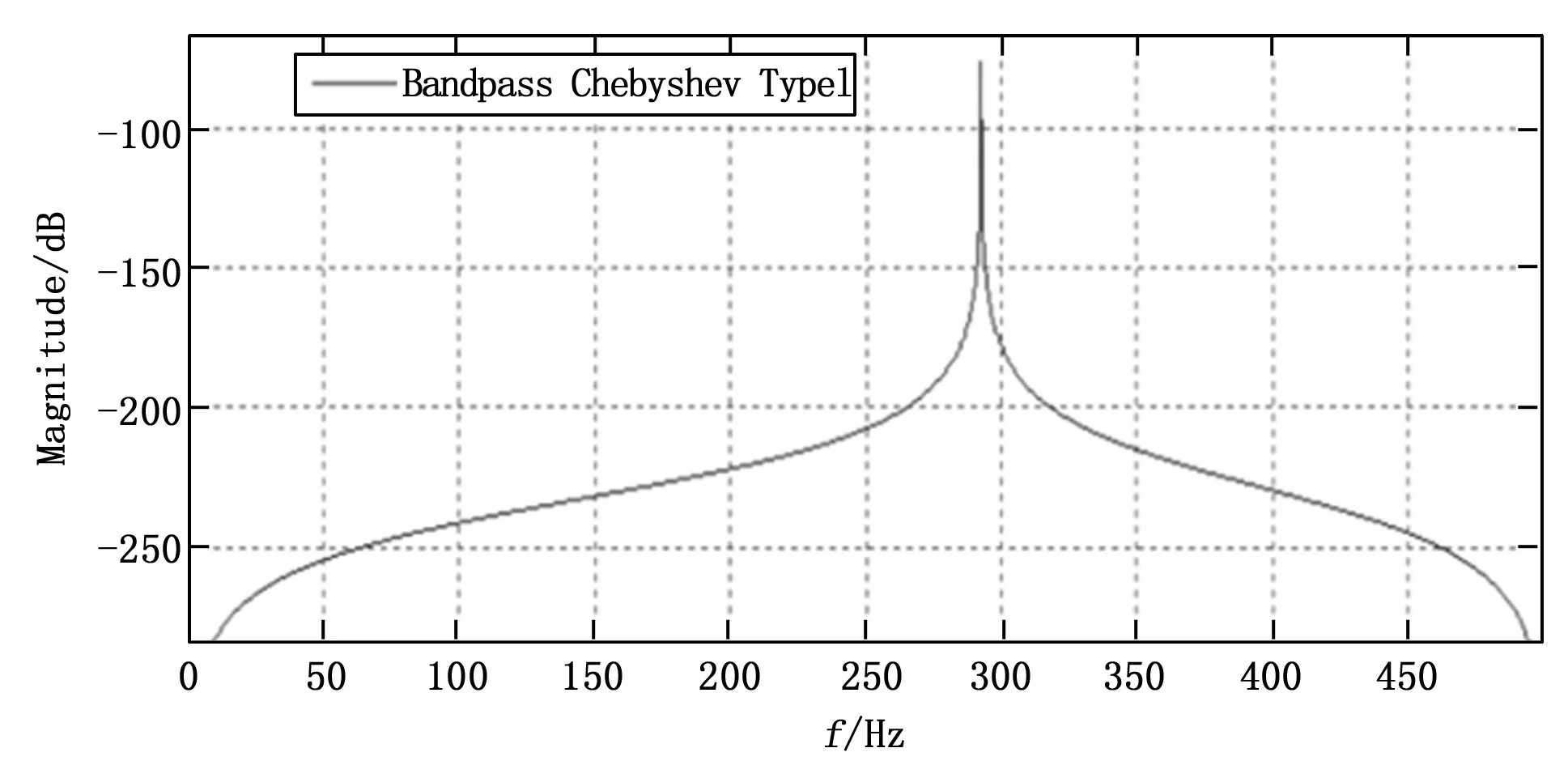
图6 第一个带通滤波器的幅频特性曲线

用相同的方法设计出另外的九个带通滤波器，导出包含有滤波器参数的C语言头文件,利用TI官方的库函数即可实现。当检测到数据计数器达到一定值后，让压缩后的数据经过第一组的10个带通滤波器，保留结果。然后对数据进行1/2重采样后，再次经过设计的10个带通滤波器。以此类推，共进行10次重抽样，每一次处理的数据量都是上一次数据量的1/2，记录输出结果。软件中利用采样数组的下标i来控制进入滤波器。第一次滤波时，采样数据全部通过10个带通滤波器；第二次下标为i和2求余等于0的数通过这十个滤波器。第n次时，下标为i和2n-1求余等于0的数通过这10个滤波器。

最后，利用RS485总线传递给上位机进行输出显示。根据纱线行业标准，波谱图横坐标为波长，纵坐标为波长对应的幅值，利用将所得到的频率与幅值的关系转化为波长与幅值的关系。同时由于分组后相邻两个滤波器波段长度是等比关系，因此选取波长的对数为横坐标。

5 实验结果与分析

根据上述对系统各模块的分析，最终设计完成了基于DSP28335的条干均匀度仪波谱图显示系统。为检测所设计系统的准确性，用该系统检测一管纱线得到波谱如图7所示。

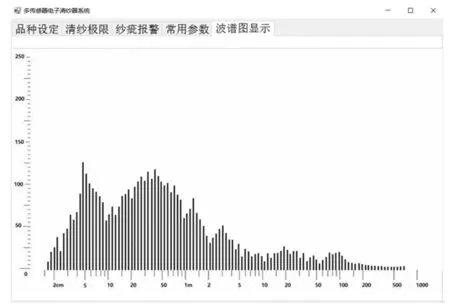
图7 纱线波谱图

由分析可知，纱线信号可视为幅值在一定范围内波动的随机信号，不具有任何周期性特征。波谱图上如果有某一波长的幅值相对比较突出，则说明该波长相对应的机械设备部位有故障，需要对该部位进行检查维修。将实验获取到的波谱图与作为棉纺行业标准的乌斯特条干均匀度仪获取到的波谱图进行对比分析，可以发现在各个波段幅值基本相同，波形的轮廓也基本相似。相对于国内条干均匀度仪产生的55个波段的波谱图，110个波段能够更精确、全面地反映出纱线的波谱结构。同时为检测系统的稳定性，对同一批纱线进行多次测量对比后，结果也基本一致。实验结果验证了该算法的可行性。

6 结论

在纱线生产过程中，条干均匀度仪波谱图通过检测纱疵的周期性特征来确定机械设备的故障位置，在实际的工业生产中具有重要的意义。采用优化算法后实现的波谱图解决了硬件电路复杂和软件计算量大的问题，采用110个带通滤波器也提高了波谱图显示的精度和显示范围，更为全面地反映出纱线的特征。系统如果想提高波谱图显示的精度，可考虑增加滤波器的数目、重新分组或优化滤波器参数等方法。这样都能够更精确快速地找到故障部位，但同时对滤波器的频带范围和DSP的运算速度有了更高的要求。该算法也可用于其他工业生产中，用来检测类似工序中的故障部位。

[1] 李俊美, 谢经明, 陈 冰, 等. 基于DSP的棉条信号波谱分析及系统实现[J]. 计算机测量与控制, 2012, 20 (3): 761-763,767.

[2] 蔡成涛, 郑 佳,韩光照. 多段电容式锅炉液位测量系统设计[J]. 计算机测量与控制, 2016, 24(7): 35-38.

[3] 招惠玲, 周美娟, 胡远忠. 电容式液位测量系统的设计[J]. 传感器技术, 2004, 23 (3): 40-41.

[4] Texas Instrument Corporation. TMS320F 28335 Digital Signal Controllers Data Manual[Z]. Texas Instrument Corporation, 2007.

[5] Johansson H. On the design of IIR bandpass filters with an adjustable bandwidth and centre frequency[J]. Circuits and Systems, 2004, 16 (1): 1-12.

[6] 宋毅珺, 宋耀良, 李文渊. 分数阶IIR和FIR滤波器及其逆系统的研究[J]. 电路与系统学报, 2011 (06): 41-45.

[7] 胡广书. 数字信号处理：理论、算法与实现(第三版)[M]. 北京：清华大学出版社，2012.

[8] 王易炜, 张金鹏, 王 龙. 基于MATLAB的数字滤波器设计及其在数据处理中的应用[J]. 航空兵器, 2011(4): 43 -47.

[9] 谢海霞, 孙志雄. IIR滤波器的DSP实现[J]. 电子器件, 2013(2): 194-196.

Realization of Spectro Graphic Algorithm of Strip Evenness

Li Zheng，Ma Jianwei

(College of Information Engineering,Henan University of Science and Technology,Luoyang 471000, China)

The spectrogram of the dryness uniformity instrument can accurately reflect the periodic characteristics of the yarn defect, so that the position of the fault in the spinning process can be quickly determined. But how to quickly and accurately realize the spectrum is always the focus of the study. Based on the resampling theorem in digital signal processing, this paper analyzes the yarn signal generated by different mechanical faults, and improves the spectral algorithm of the uniformity of the strip. The algorithm builds 110 different wavelengths bandpass filter in the wavelength range that needs to be observed, according to the adjacent filter band relationship grouping analysis. Through the DSP28335 microprocessor data acquisition, signal processing and host computer spectrum display system experiments, the results prove the feasibility of the algorithm. The improved algorithm greatly reduces the complexity of the hardware used in the past, improves the operation speed and increases the observable range of the spectrum, and can detect the fault position more accurately.

spectro graphic; mechanical failure; bandpass filter

2017-02-15；

2017-03-03。

国家自然科学基金项目(U1504617)。

李 征(1991-)，男，河南省平顶山市人，硕士研究生，主要从事嵌入式系统开发方向的研究。马建伟(1965-)，男，河南巩义人，教授，博士生导师，主要从事自动化测量、控制与组合导航方向的研究。

1671-4598(2017)08-0179-04

10.16526/j.cnki.11-4762/tp.2017.08.046

TN911.72

A