对认证加密算法AES-OTR的伪造攻击
2017-11-01郑秀林付伊鹏宋海燕
郑秀林 付伊鹏 宋海燕
1(北京电子科技学院 北京 100070)
2(西安电子科技大学 陕西 西安 710071)
对认证加密算法AES-OTR的伪造攻击
郑秀林1,2付伊鹏2宋海燕2
1(北京电子科技学院 北京 100070)
2(西安电子科技大学 陕西 西安 710071)
AES-OTR算法是CAESAR竞赛中的一个竞选算法,CAESAR竞赛是2014年在国际密码协会IACR主办下由日本发起面向全球的征集认证加密算法的竞赛活动。AES-OTR凭借自身独特的优点顺利进入了第三轮的筛选,该算法加密和认证都是基于分组密码AES。但是AES-OTR加密时各块的相对独立性以及简单的标签产生方法,使得存在有效的伪造攻击方法。针对该算法的这些缺点,提出在已知明文条件下,当关联数据和公共消息数重用时对AES-OTR的伪造攻击方法,同时证明了伪造方法的有效性,并且计算了伪造方法成功的概率。
AES-OTR算法 认证加密 伪造攻击 分组密码
0 引 言
我们知道保密性[1]和完整性[2]是信息安全的两大核心目标,保密性是对抗敌手的被动攻击,保证信息不泄露给未经授权的一方。完整性是对抗敌手的主动攻击,防止信息被未授权的一方修改、伪造。认证加密算法能够同时保证信息的机密性和完整性,是一种同时具有加密和认证两种属性的密码算法。目前大量的信息在传输过程中不但需要保密,而且接收者收到信息后还需要对信息进行认证,保证信息在传输过程中的保密性、完整性和真实性。因此对于认证加密算法的设计和研究就显得非常必要了,CAESAR竞赛[3]共征集到 57个算法,要经过三轮筛选,预计到2017年12月底公布最终的胜选算法,目前正处于第三轮安全性评估阶段。认证加密算法不同于之前的加密算法,其加密后的输出不仅有密文C,还有与密文或明文有关的标签T,在发送给接收方时,C和T要一起发送过去。当接收方收到信息后,分离出C和T,之后用解密算法对密文C进行解密,同时产生一个新的标签T′ ,这个标签与由C解密后得到的明文有关,因此如果密文C在传输过程中被人篡改,那么产生的T′和T是不一样的,这时解密得到的密文是无效的,如果T′和T相等,那么解密得到的明文是有效的明文,文献[4]的第17章对认证加密算法的定义及发展情况有详细的描述。伪造攻击[5]就是在改变密文的情况下,同时又做到不被接收方察觉,也就是能够通过解密验证,使得解密后的明文是有效的。
AES-OTR[6]算法是基于分组密码AES[7]设计的认证加密算法,该算法在密文产生阶段用到了公共消息数N,标签产生阶段用到了关联数据A。
1 AES-OTR算法的描述
1.1 基本符号
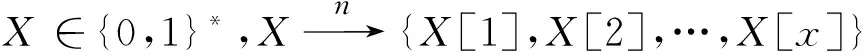
如果没有别的说明n一般取128,Ek代表的是AES加密函数,其中的密钥为k,|k|∈{128,192,256}。对于X,Y∈{0,1}n,Y=Ek(X)表示明文X在密钥k下,通过AES加密后的密文是Y。
1.2 输入和输出
Κae、Nae、Aae、Mae、Cae、Tae分别表示密钥集合、公共消息数集合、关联数据集合、明文集合、密文集合和标签集合,在这里,Kae∈{0,1}|K|,Nae∈{0,1}|N|,Aae={0,1}8*,Mae=Cae={0,1}8*,Tae={0,1}τ其中τ∈{32,40,…,128}。
加密算法需要下列序列:
• 密钥K∈Κae
• 公共消息数N∈Νae
• 关联数据A∈Αae
• 明文M∈Μae
输出序列为:密文(C,T)∈Cae×Tae
解密算法需要下列序列:
• 密钥K∈Κae
• 公共消息数N∈Νae
• 关联数据A∈Αae
• 密文(C,T)∈Cae×Tae
输出序列为:明文M∈Μae或者为无效的信息记为⊥。
1.3 AES-OTR的加密和标签的产生
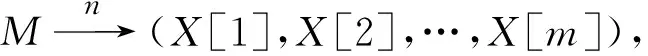
C[2i-1]=Ek(2i-1L⊕M[2i-1])⊕M[2i]
(1)
C[2i]=EK(2i-1L⊕δ⊕C[2i-1])⊕M[2i-1]
(2)
因为是两两分组,所以分为m是奇数和偶数两种情况,这两种情况的不同之处是对最后一块明文的处理不同,如图2所示。加密过程用到L和δ,这两个参数都是对公共消息数N进行处理得到的,图3是对关联数据A的处理,由关联数据得到TA,标签T的产生过程用到了TA。图4中Σ的表达式与m的奇偶有关,当m为偶数时:
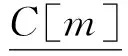
(3)
L*=2l-1L⊕δ
(4)
当m为奇数时:
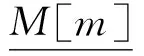
(5)
L*=2l-1L
(6)
发送者将图1、图2和图4得到的密文C和标签T发送给接收方,其中C=C[1]‖C[2]‖…‖C[m]。
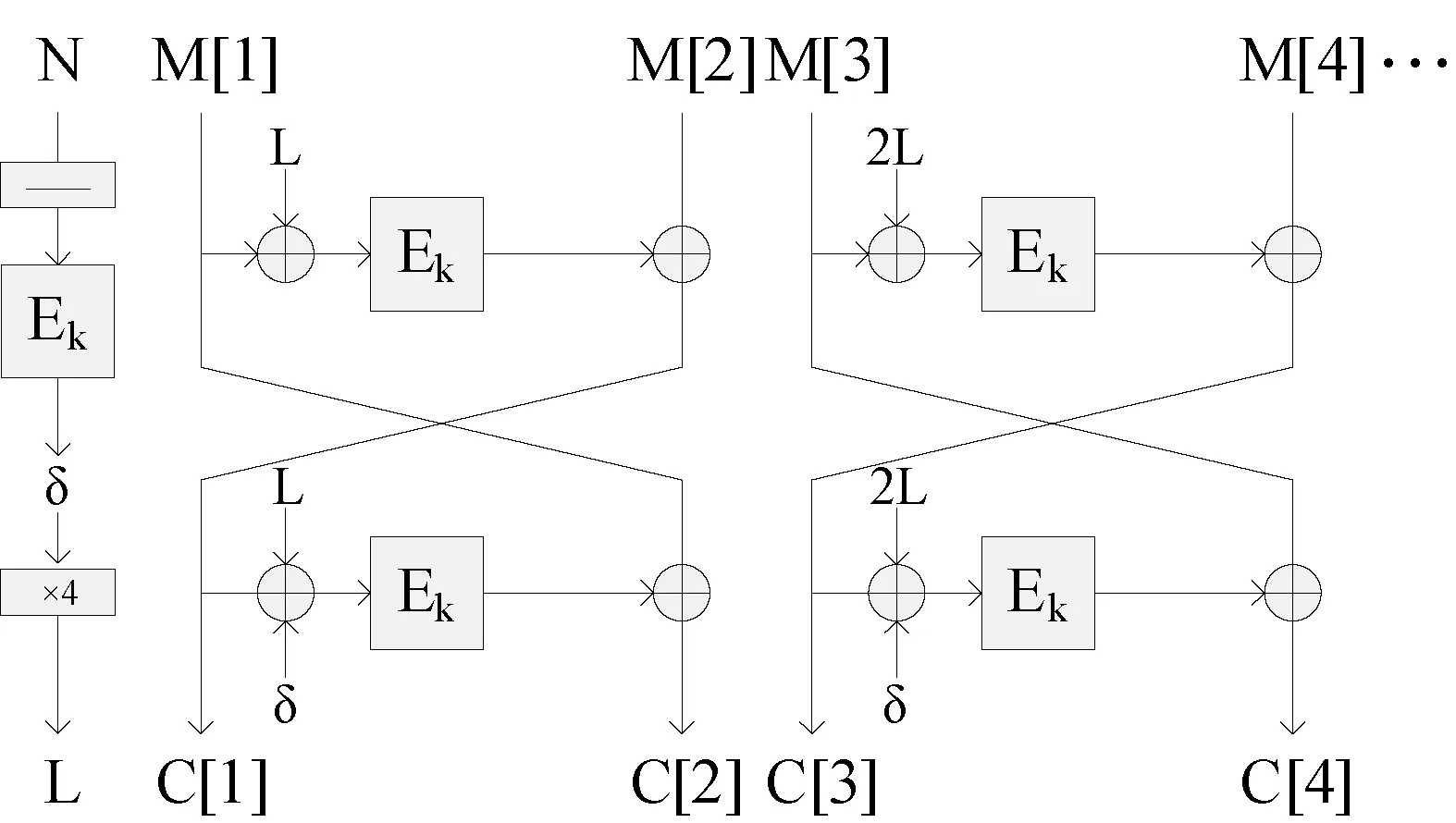
图1 AES-OTR算法对明文(除去最后一组)的处理过程
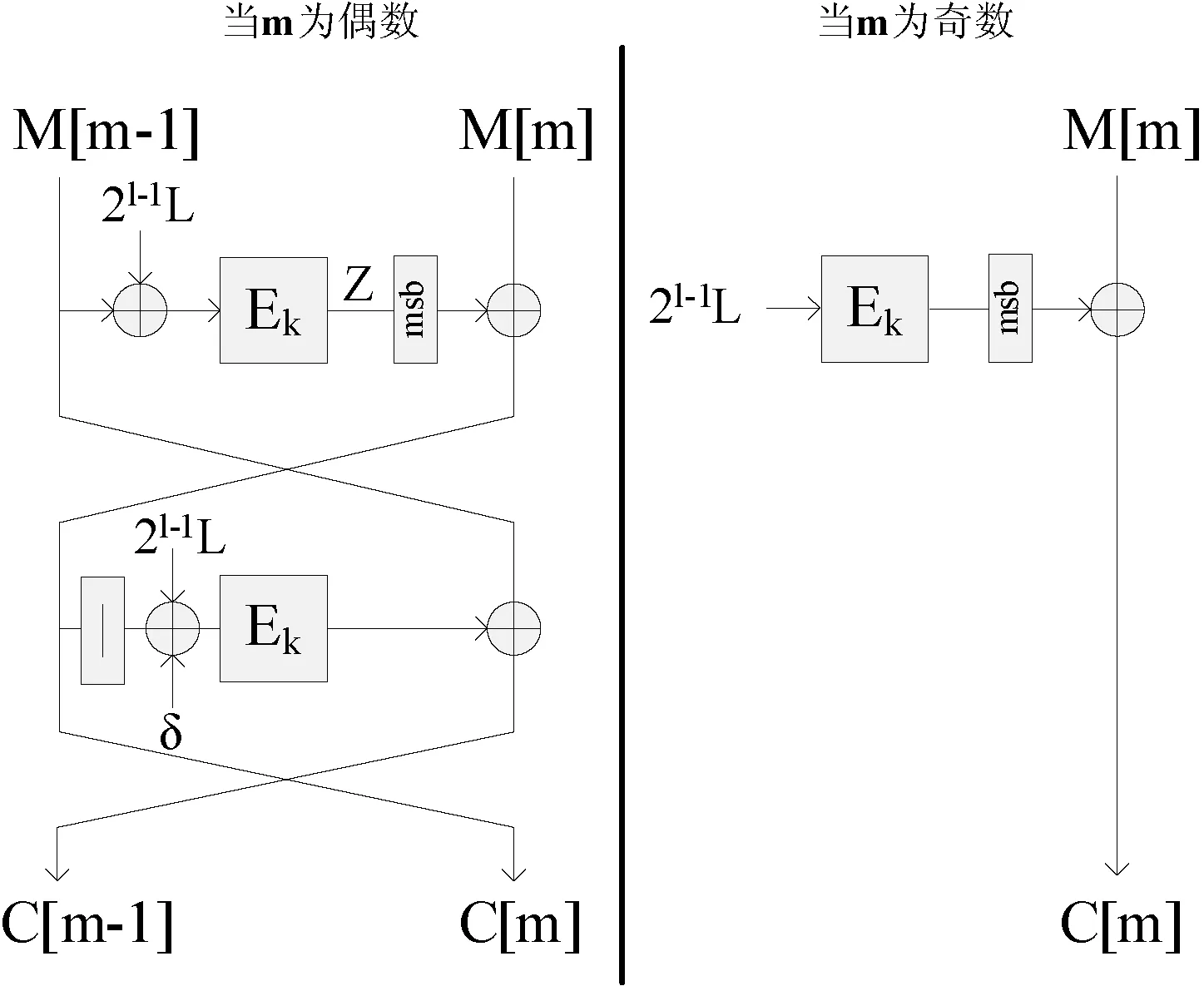
图2 AES-OTR对最后一组明文的处理过程
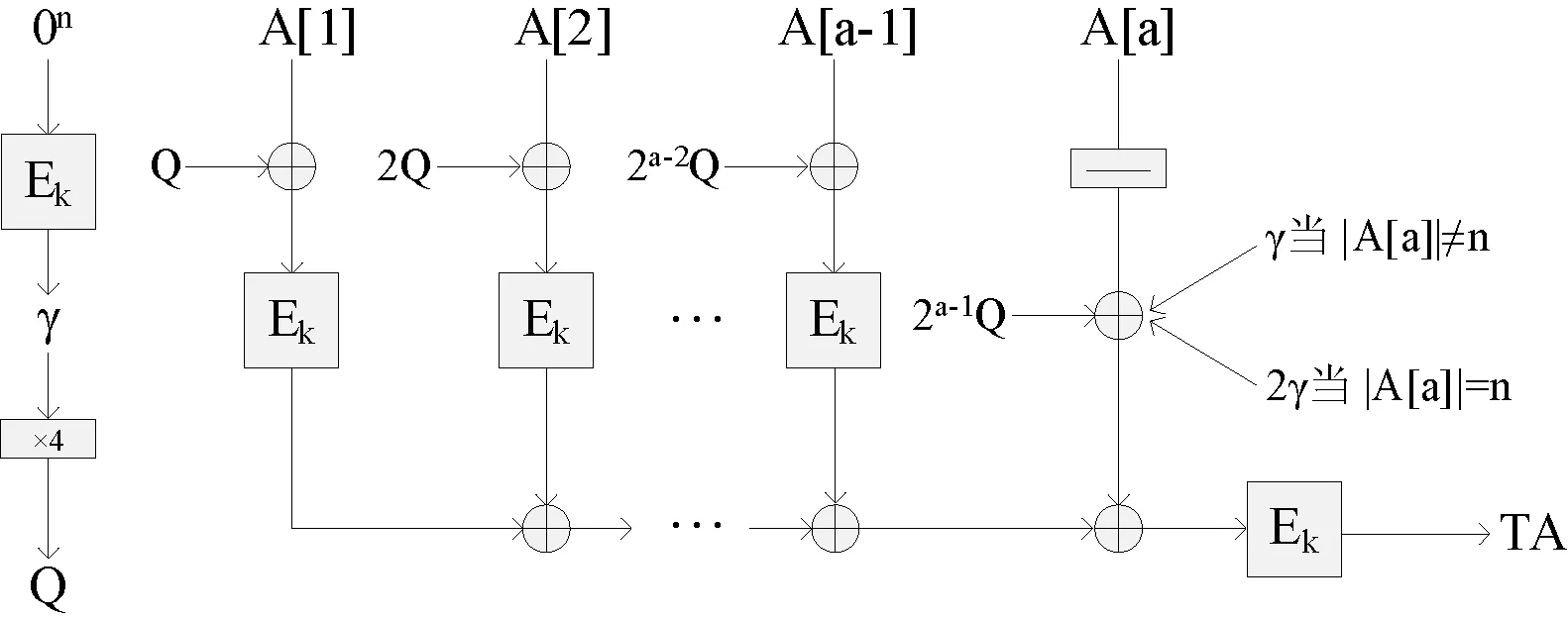
图3 由关联数据A得到TA

图4 标签的生成过程
1.4 AES-OTR的解密和验证
当接收方收到(C,T)后,通过N、A、C和解密算法可以得到M和T′。如果T′=T,那么解密得到的明文M是有效的,如果T′≠T,那么得到的M是无效的。解密过程和加密过程非常类似,这里不再赘述,具体过程可以参考文献[2]。
2 对AES-OTR的伪造攻击
设我们手中有s+1对明密文,下面分别讨论s=0和s>0这两种情况下伪造成功的概率,当s=0时,也就是仅仅知道一对明密文,当s>0时,即知道多对明密文。
2.1 s=0时的伪造攻击
设已知的明文为M,经加密后得到(C,T),伪造的密文记为(C*,T*),解密后的明文记为M*。
2.1.1 伪造方法介绍
首先对明文M和C进行分块(在这里要求明文长度|M|必须是n的倍数,且为奇数倍),
其中m是奇数且对于1≤i≤m,|M[i]|=n,我们设M*和C*的分块结果为:
其中m是奇数,最后一块的长度不一定是n。设r=(m-1)/2,下面分三种情况进行讨论:
1) 如果存在一个i∈{1,2,…,r}满足如下式子:
C[2i-1]⊕M[2i]=C[2i]⊕M[2i-1]
(7)
通过式(1)和式(2)我们得到:
δ=M[2i-1]⊕C[2i-1]
(8)
如果我们选择|M*[m]| pad(M*[m])=M[m]⊕M[2i-1]⊕C[2i-1] (9) 当1≤k (10) 那么其解密后对应的密文为: 当1≤k (11) C*[m]=msb|M*|(C[m]⊕M[m])⊕M*[m] (12) 因此我们选择式(11)、式(12)所示的密文,标签选择T*=T,此时(C*,T*)是有效的。 2) 如果存在两个不等的数i,j∈{1,2,…,r}满足: C[2i]⊕M[2i-1]=C[2j]⊕M[2j-1] (13) 通过式(2)得到: 2i-1L⊕C[2i-1]=2j-1L⊕C[2j-1] (14) 对式(14)进行变形得到: 2i-1L⊕M[2i-1]= 2j-1L⊕C[2j-1]⊕ M[2i-1]⊕C[2i-1] (15) 通过式(1)和式(15)得到: C[2i-1]⊕M[2i]= Ek(2j-1L⊕C[2j-1]⊕M[2i-1]⊕C[2i-1]) (16) 如果我们选择如下明文: M*[2j-1]=C[2j-1]⊕M[2i-1]⊕C[2i-1] (17) M*[2j]=C[2i-1]⊕M[2i]⊕C[2j-1] (18) M*[m]=M[m]⊕M[2j]⊕C[2i-1]⊕ M[2i]⊕C[2j-1] (19) 当k∉{2j-1,2j,m}时,M*[k]=M[k] (20) 由明文得到密文为: C*[2j]=C[2j]⊕M[2j-1]⊕C[2j-1]⊕ M[2i-1]⊕C[2i-1] (21) C*[m]=C[m]⊕M[2j]⊕C[2i-1]⊕ M[2i]⊕C[2j-1] (22) 当k∉{2j,m}时,C*[k]=C[k] (23) 因此我们选择式(21)-式(23)所示的密文,标签选择T*=T,此时(C*,T*)是有效的。 3) 如果存在两个不等的数i,j∈{1,2,…,r}满足: M[2i]⊕C[2i-1]=M[2j]⊕C[2j-1] (24) 通过式(1)得到: M[2i-1]⊕M[2j-1]=2i-1L⊕2j-1L (25) 如果我们选择如下明文: M*[2j]=M[2i]⊕M[2i-1]⊕M[2j-1] (26) M*[2i]=M[2j]⊕M[2i-1]⊕M[2j-1] (27) 当k∉{2j,2i}时,M*[k]=M[k] (28) 其对应的密文是: C*[2j]=C[2i]⊕M[2i-1]⊕M[2j-1] (29) C*[2i]=C[2j]⊕M[2i-1]⊕M[2j-1] (30) C*[2i-1]=C[2j-1]⊕M[2i-1]⊕ M[2j-1] (31) C*[2j-1]=C[2i-1]⊕M[2i-1]⊕ M[2j-1] (32) 当k∉{2j,2i,2j-1,2i-1}时,C*[k]=C[k] (33) 因此我们选择式(29)-式(33)所示的密文,标签选择T*=T,此时(C*,T*)是有效的。 2.1.2 证明(C*,T*)的有效性 要想证明(C*,T*)的有效性,需要证明C*解密后得到的标签T′和收到的标签T*相等。 对于情况一,首先M*[m]的长度不是n,由图4我们知道标签的产生发生了变化,因为TA未变化,因此要想证明T′=T*(即T),需要证明TE′=TE,由式(8)和式(9)得到pad(M*[m])=M[m]⊕δ,由TE的产生方法以及3L*未变化,可以得到TE*=TE,那么解密得到的标签T′=T即T′=T*。 对于情况二,由式(18)和式(19)我们得到M*[2j]⊕M*[m]=M[2j]⊕M[m],由此我们保证了Σ的值没有变化,而3L*、δ和明文最后一块的长度也没变化,因此,保证了标签值未变化,即T′=T,也就是T′=T*。 对于情况三,由式(26)和式(27)我们得到M*[2i]⊕M*[2j]=M[2i]⊕M[2j],由此我们保证了Σ的值没有变化,而3L*、δ也没变化,因此保证了标签值未变化,即T′=T,也就是T′=T*。 2.1.3 计算伪造成功的概率 计算成功的概率P,需要把式(7)、式(13)、式(24)成功的概率相加,设式(7)、式(13)、式(24)成功的概率分别为P1、P2、P3,则: (34) 进一步计算得P=r2·2-n。 假设我们的手中有s+1对明密文对可用,分别记为M0、M1、…、Ms,他们对应的密文和标签分别记为(C0,T0)、(C1,T1)、…、(Cs,Ts),我们的目标是伪造出一对有效的带标签的密文,不妨借用M0的标签,伪造的密文记为(C*,T*),其中T*=T0。 2.2.1 伪造方法介绍 伪造算法F0: 第一步在加密过程中,首先对s+1对明文进行分块,如下所示: ⋮ 以上s+1对明文对应的密文分块为: ⋮ 我们设m=min(m0,m1,…,ms),r=「m/2⎤-1。 第二步我们寻找满足下面等式的明文块, M0[k1]⊕M0[k2]⊕…⊕M0[ki]= Mt1[k1]⊕Mt2[k2]⊕…⊕Mti[ki] (35) 其中2≤i≤r,k1,k2,…,ki∈{2,4,…,2r}且k1 第三步找到一组(k1,k2,…,ki)和(t1,t2,…,ti),那么我们伪造的密文C*是将C0中的C0[kj-1]和C0[kj]替换为Ctj[kj-1]和Ctj[kj];这样就得到C*,用公式表示即对于1≤q≤r: C*[2q-1]‖C*[2q]= (36) 对于2r (37) 此时我们已经构造出了C*,标签为T*=T0。 2.2.2 证明(C*,T*)的有效性 要证明(C*,T*)的有效性,根据前面介绍的AES-OTR解密验证,我们需要证明C*解密后的得到的标签T′满足T′=T*(即T0)。 首先计算C*解密后得到的明文的表达式,根据式(36)和式(37),以及已知的明密文的对应关系,我们可以得到M*的表达式,用公式表示即当1≤q≤r时: M*[2q-1]‖M*[2q]= (38) 对于2r (39) 由图4我们知道了标签T由Σ、|M|、N和A决定,N和A没变,根据式(38)和式(39)我们知道|M*|=|M0|,接下来只需要证明Σ*=Σ0即可。 根据AES-OTR的加密,我们得到Σ*和Σ0的计算公式(这里我们假设m0为偶数,奇数情况与此类似)。 (40) (41) Σ*⊕Σ0=Mt1[k1]⊕Mt2[k2]⊕…⊕Mti[ki]⊕ M0[k1]⊕M0[k2]⊕…⊕M0[ki] (42) 根据式(35)得到: Σ*⊕Σ0=0 (43) 即Σ*=Σ0,综上(C*,T*)是有效的。 2.2.3 计算伪造成功的概率 下面我们伪造算法成功的概率,在这里我们假设已知的明文都是随机且独立[9]的。 设Pi表示式(35)成功的概率,那么伪造算法F0成功的概率为: (44) 根据文献[9]中的概率论知识,我们可以得到: (45) 那么: (46) 对于i≥2,下面不等式(47)一定成立: (47) 则式(46)可以变为: (48) 将常数项提到前边,并且进一步计算得到: (49) 当r较大时(如r>10),r+1相比于2r可以忽略;我们知道2n(n一般取128)是一个非常大的数,因此根据文献[10]中等价无穷小的知识,我们可以得到1-(1-1/2n)s2的等价无穷小为s2/2n。 因为s+1对明密文对中有s+1个标签可用,所以伪造成功的概率为s2(s+1)2r-n。 明密文对各自也可独立进行伪造,方法和第一种情况一样,但是因为这个概率相比于s2(s+1)2r-n非常的小,并且还要求明文最后一块必须是n的倍数且m必须是奇数,因此2.2.3节的计算忽略了这个概率。 本文针对AES-OTR 算法的特点,分别提出了仅仅知道一对明密文和多对明密文的情况下的伪造攻击方法,并且分别证明了算法的有效性,计算了算法成功的概率,这对于AES-OTR算法的安全性分析有重要参考意义的。式(7)、式(13)、式(24)三个式子的编程查找是容易实现的,而式(35)的快速有效的编程查找并不容易,将作为下一步的研究目标。 [1] Lo A,Grotevant H,McRoy R.Privacy and Confidentiality in Adoption Research:Perspectives from the Minnesota/Texas Adoption Research Project[D].University of Massachusetts Amherst,2016. [2] Sumra I A,Hasbullah H B,AbManan J B.Attacks on security goals (confidentiality,integrity,availability) in VANET:a survey[M]//Vehicular Ad-Hoc Networks for Smart Cities.Springer Singapore,2015:51-61. [3] CAESAR-Competition for Authenticated Encryption:Security,Applicability,and Robustness(2014)[OL].http://competitions.cr.yp.to/Caesar.html. [4] 吴文玲.分组密码的设计与分析[M].北京:清华大学出版社,2009:371-391. [5] Nandi M.Forging attacks on two authenticated encryption schemes COBRA and POET[C] //International Conference on the Theory and Application of Cryptology and Information Security.Springer Berlin Heidelberg,2014:126-140. [6] Minematsu K.Parallelizable rate-1 authenticated encryption from pseudorandom functions[C] //Annual International Conference on the Theory and Applications of Cryptographic Techniques.Springer Berlin Heidelberg,2014:275-292. [7] Daemen J,Rijmen V.The design of Rijndael:AES-the advanced encryption standard[M].Springer Science & Business Media,2013. [8] Suzaki T,Minematsu K.Improving the generalized Feistel[C]//International Conference on FAST Software Encryption.Springer-Verlag,2010:19-39. [9] 王志江.概率论与数理统计[M].北京:高等教育出版社,2011. [10] 赵修坤.微积分[M].3版.北京:国防工业出版社,2012. FORGINGATTACKSONAUTHENTICATEDENCRYPTIONALGORITHMAES-OTR Zheng Xiulin1,2Fu Yipeng2Song Haiyan2 1(BeijingElectronicsScienceandTechnologyInstitute,Beijing100070,China)2(XidianUniversity,Xi’an710071,Shaanxi,China) AES-OTR algorithm is a campaign of CAESAR competition, the competition is sponsored by the international cryptography Association IACR and launched by Japan in order to collect authentication and encryption algorithm to the whole world. AES-OTR has successfully entered the third round of screening by virtue of its unique advantages. Encryption and authentication of AES-OTR algorithm are all based on block cipher AES. But the relative independence of each block and label generation method is relatively simple make AES-OTR exists effective methods of forgery attack. For the disadvantages of this algorithm, this paper shows forgery attack on AES-OTR in the known plaintext conditions and association data and public message number are reused. At the same time, the validity of the methods is proved, and the probability of the success of the method is calculated. AES-OTR algorithm Authentication and authorization Forgery attack Block cipher TP309.7 A 10.3969/j.issn.1000-386x.2017.10.057 2016-12-22。郑秀林,教授,主研领域:分组密码和序列密码的设计与分析。付伊鹏,硕士生。宋海燕,硕士生。2.2 s>0时的伪造攻击

3 结 语
