基于DSP的机器人末端力控制系统设计
2017-11-01汪步云许德章
王 志,汪步云,许德章
(1.芜湖安普机器人产业技术研究院,安徽 芜湖 241000; 2.安徽工程大学 机械与汽车工程学院,安徽 芜湖 241000)
基于DSP的机器人末端力控制系统设计
王 志1,汪步云2,许德章2
(1.芜湖安普机器人产业技术研究院,安徽 芜湖 241000; 2.安徽工程大学 机械与汽车工程学院,安徽 芜湖 241000)
工业机器人的运动分为自由运动和受力约束运动两种不同的运动类型;受力约束运动不仅要进行精确的位置控制,而且要对接触力进行精确控制;文章对机械臂的末端力控制系统进行了研究;采用了高精度电动滑台作为力控制系统的执行机构,在电动滑台末端增加了柔性单元,从而克服了系统柔性不足的缺点,并且依据Lyapunov稳定性理论确定系统的二阶参数,使用Narendra提出的稳定自适应设计方法构建了电动滑台的数学模型;对机械臂末端柔顺系统的系统设计及算法进行了研究,消除了外界噪声对系统的干扰,解决了力控制的基本控制策略问题,优化了力控制时系统的响应特性。
工业机械臂;阻抗控制;受力约束运动
0 引言
传统规划控制算法对受力约束控制无法达到令人满意的控制效果,力约束控制不仅要进行精确的位置控制,而且必须对力接触进行精确控制,如果不能对力进行精确控制,则可能在工作过程中损坏设备[1]。受力约束控制又称为柔顺控制,柔顺控制就是利用能反映外部力的传感器对工业机器人的运动轨迹进行调整,使得工业机械臂对外界空间力的变化有响应的能力,因此,我们称工业机械臂对外界环境具有柔顺性[2]。文章采用阻抗控制方法对系统进行力控制。
1 系统的整体设计方案
总体设计思想是:利用高精度轻载电动滑台作为执行机构,当柔顺机构处于位置控制模式运动时候,系统根据预先规划好的路径运动;当外界接触力超过切换阀值时,切换至力控制模式,同时,力控制模式下根据事先设定好的额定压力值进行运动,这个模式也称之为恒力控制模式[3]。这个过程就是完整的力控制。整体设计思想如图1所示。
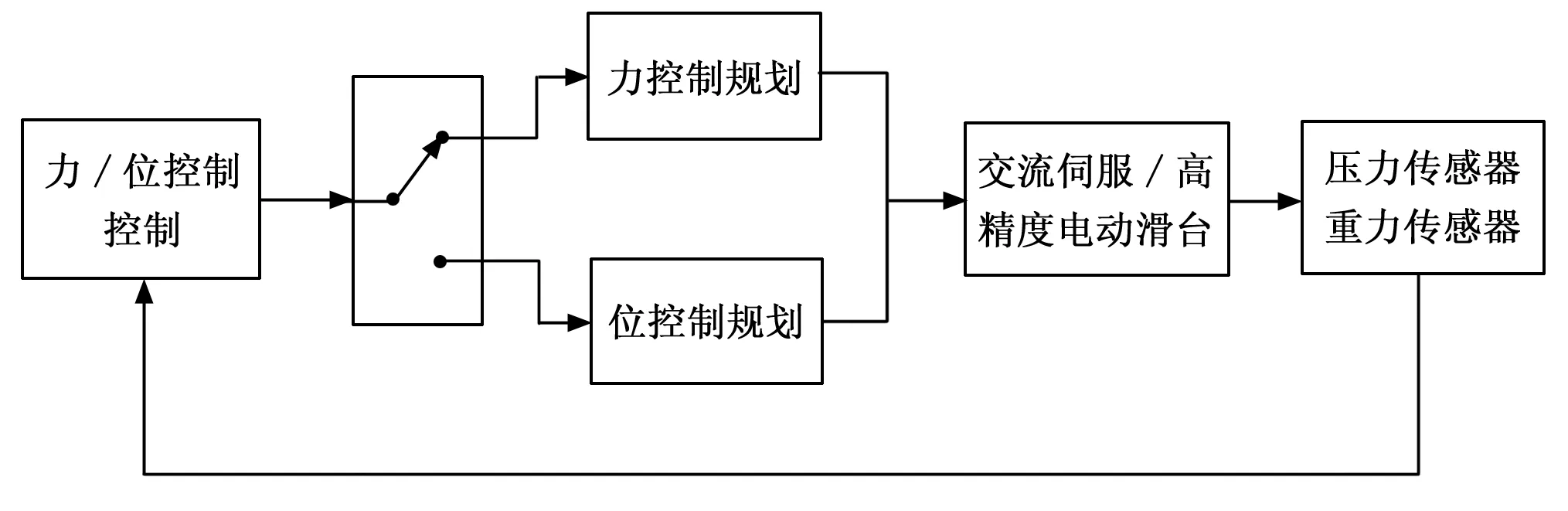
图1 柔顺控制总体设计方案
2 高精度电动滑台的数学建模
柔顺系统的电动滑台的动力学模型为图2所示。
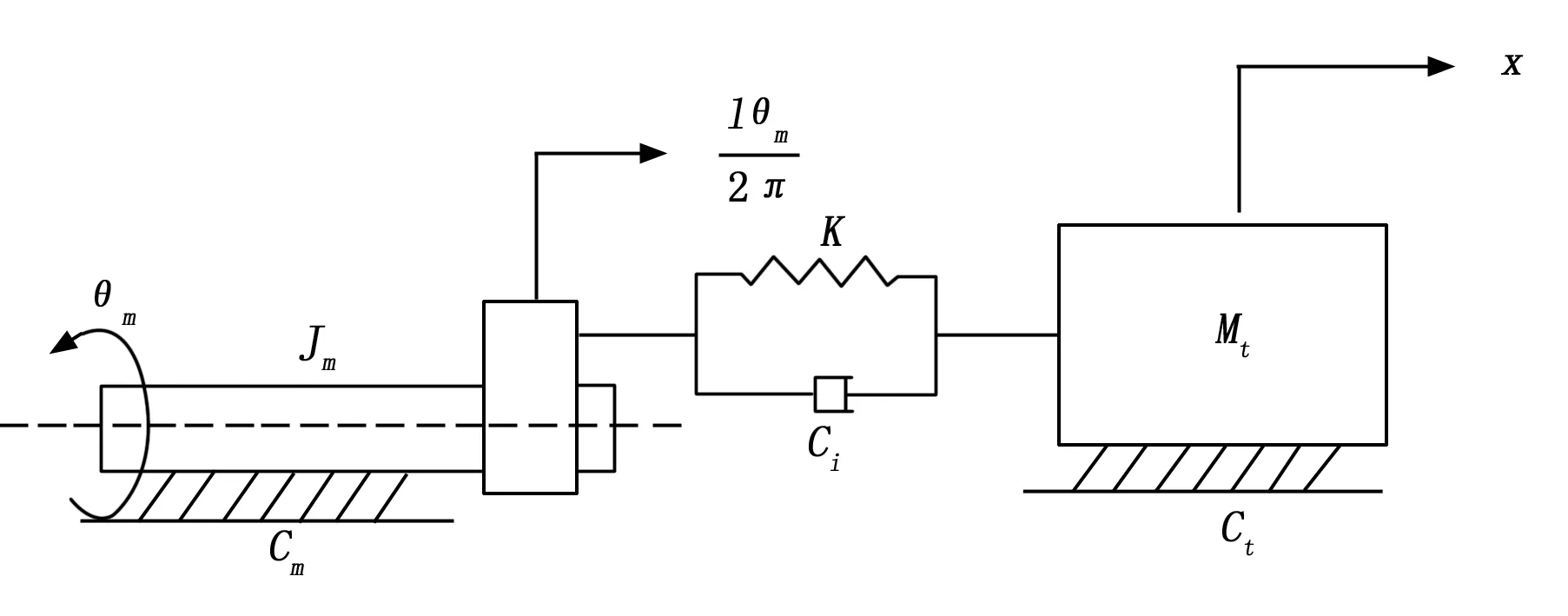
图2 电动滑台动力学模型
图2中,Jm为旋转零件的总转动惯量;θm为滚珠丝杠的转角;T为伺服电机的力矩值;K为传动系统的轴向刚度;ct为直线导轨的粘性摩擦系数;ci为传动系统轴向粘性摩擦系数;cb为旋转零件的总粘性摩擦系数;Mt为柔性元件和滑台的质量。
文章根据Lyapunov稳定性理论确定系统的二阶参数,使用Narendra提出的稳定自适应设计方法构建了电动滑台的数学模型[5]。由此得到电动滑台的传递函数:
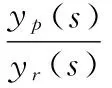
(1)
将电动滑台的主要技术参数带入公式(1),得到传递函数:
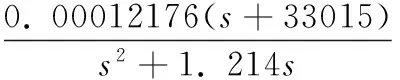
(2)
3 柔性元件的数学建模
柔性元件主要由圆柱螺旋弹簧、3D打印结构部件、阻尼器、圆柱导轨及直线轴承构成。
由物理学分析可以把阻尼元件、圆柱导轨和直线轴承视作阻尼器;结构部件和压力传感器视作质量块(物体);圆柱螺旋弹簧视作理想弹簧。柔性元件的力模型简化如图3所示。

图3 柔性元件力学模型
根据材料的已知特性:论文把圆柱形螺旋弹簧视作理想的弹簧,忽略弹簧的阻尼[6]。且已知弹簧的弹性系数k=0.5 N/M;阻尼器的阻尼系数随着速度的变化而发生变化,且其摩擦力和速度的大小成正比关系,论文把比例系数设为阻尼系数c=0.1;压力传感器和3D打印结构质量和为0.25 kg;由于圆柱导轨和直线轴承之间的摩擦力非常小,所以论文取摩擦力f0=0。
设系统的输入力大小为u(t),输出力大小为y(t),柔性元件的阻尼器其摩擦力大小为fdy(t)/d(t),可以的得到系统的运动方程:
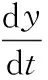
(3)
则可以得到系统的传递函数为:
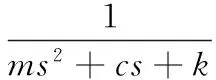
(4)
把已知值代入传递函数,可以得带柔性元件的传递函数:
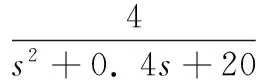
(5)
4 压力信号的改进型小波阀值降噪
信号在采样和传输过程之中,难免会夹杂一些噪声信号,从而造成信号的失真,若直接将染上噪声的信号作为控制系统的输入信号,则会极大地影响传感器补偿后的精度,增加系统误差,降低了传感器补偿的意义。因此,文章采用改进型小波阀值算法进行力信号的降噪处理。改进型小波阀值函数如公式(6)。
(6)
为了验证改进型阀值函数的降噪效果,在MATLAB的小波工具箱中采用DB4小波为母小波;输入的原信号使用sref信号,干扰信号使用高斯白噪声;采样的数据长度为2000,小波的分解层数为4层,并与传统软阀值降噪算法、硬阀值降噪算法、文献[4]算法作了比较,验证算法降噪效果。

图4 软阀值及硬阀值降噪信号

图5 改进型小波阀值函数降噪及文献[4]算法出现的剧烈振荡

降噪算法硬阀值降噪软阀值降噪改进型阀值降噪信噪比/db24.861124.819924.8842均方误差/db1.33711.40501.0339
图4左上图是原始方波信号,右上图是加过高斯白噪声后的信号,左下图是通过小波软阈值函数处理过的信号,右下图是小波硬阈值函数处理过的信号。综合图4可以看出软阀值降噪在细节处理上较为模糊,不过没有明显的振荡;在对细节信号的处理上,硬阀值降噪比软阀值降噪好,但是可以看到处理后的信号有明显的振荡。图5中改进型阀值降噪相对于软阀值降噪细节部分保留较好,也没有硬阀值算法和文献[4]算法降噪时明显的振荡,其最终降噪效果要好于其它三种算法。
根据表1信噪比SNR数据进行分析,可以看出改进型阀值降噪的信噪比SNR值为24.884 2,稍大于硬阀值和软阀值算法;再从MSE均方误差来看,改进型阀值降噪均方误差值位1.033 9,远小于前两种传统的算法;根据表1分析新的算法在降噪效果上较传统算法有一定优势。
5 力控制的PI参数模糊自整定
机械臂末端柔顺系统的参数模糊自适应整定的原理如图6所示。

图6 PID参数模糊自整定
图6中,FD是系统预设的压力值;Fm是经过重力补偿后得到的力传感器测量值,也就有实际接触的力;Fecc是当前的力误差和上一时刻力误差间的差,也就是力误差变化量;Fec是期望力值和实际接触力值之间的差,也就是力误差;模糊控制系统的输入力误差变化量Fecc与Fec,通过模糊推理后输出量即ΔKp、ΔKi、ΔKd,也就是PID比例、积分、微分参数的调整量;θ是通过运动学计算后控制器发给力控制系统的控制量;x0是DSP的预设轨迹;Vn是PID控制的输出量,也就是机器人末端柔顺系统在工件坐标系里的调整速度。
以控制系统的响应速度、稳定性、稳态精度和超调量几方面作为指标来进行分析,Kp、Ki、Kd三个调整量的作用如下。Kp:加快系统的响应速度,提高系统的精度;Ki:消除控制系统静态误差;Kd:改善了控制系统的动态特性,抑制系统的偏差变化量。根据实验及仿真可以得出模糊自适应调整PI参数的调整规则如表2所示。
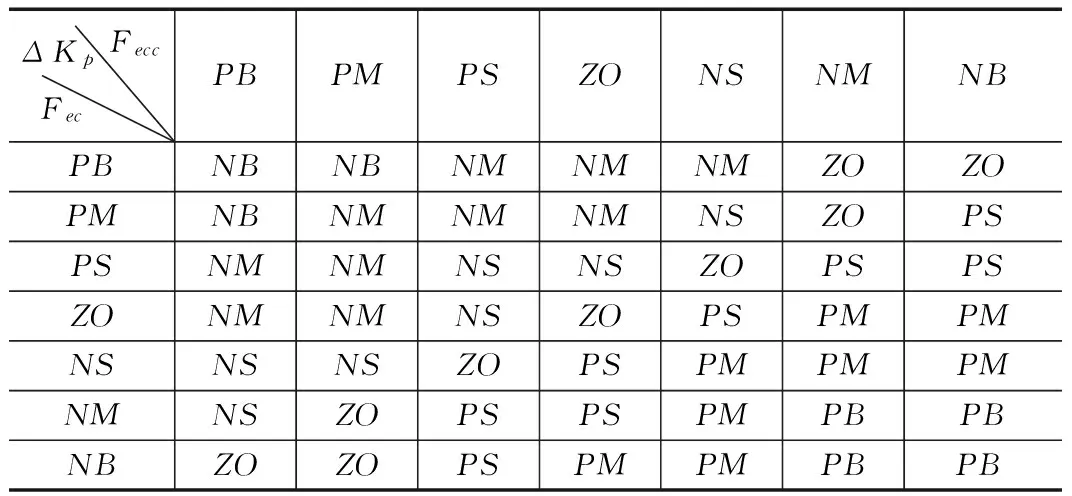
表2 参数ΔKp调整模糊规则
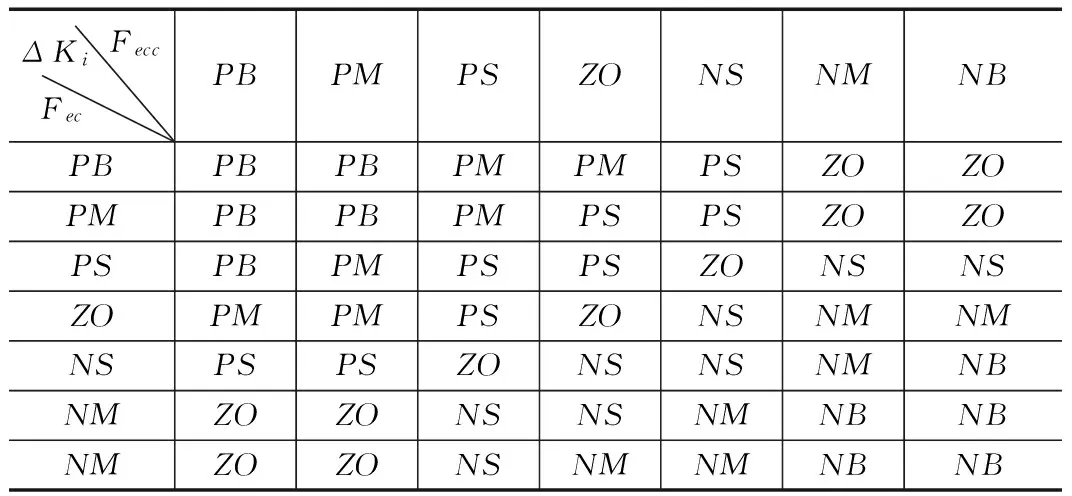
表3 参数ΔKi调整模糊规则
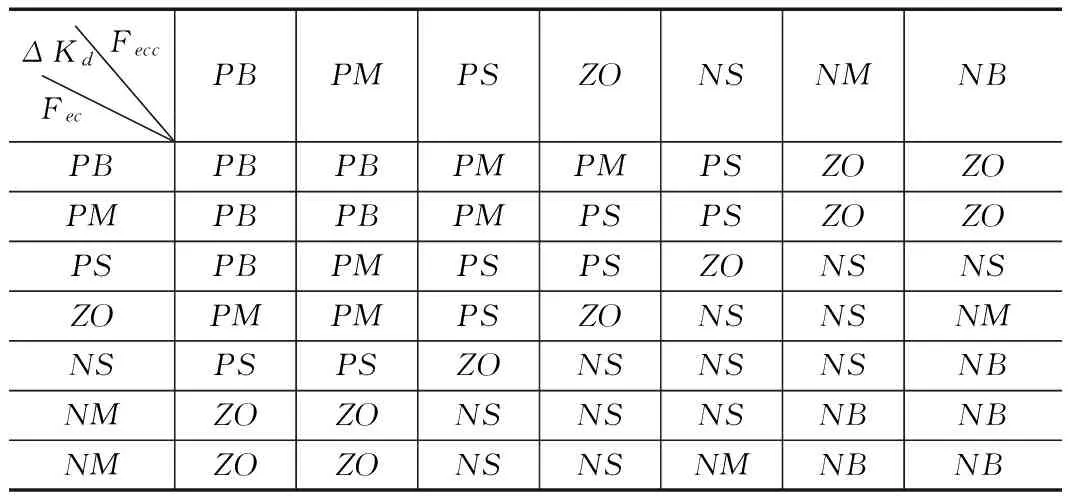
表4 参数ΔKd调整模糊规则
根据图6的PID参数模糊自整定方法,并带入前文的电动滑台和柔性单元的传递函数,可以得到系统的模糊控制SIMULINK仿真图见图7。
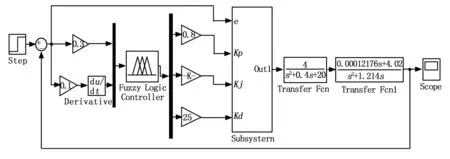
图7 PID参数模糊自整定仿真
带入整定好的模糊参数,仿真设定接触力为4.5 N,仿真结果见图8,其中实线是期望力,虚线是系统跟踪力曲线;在0.3 s时,期望力为4.5 N,系统跟踪曲线在0.6 s左右达到4.5 N收敛并趋于稳定,系统没有出现明显的超调。
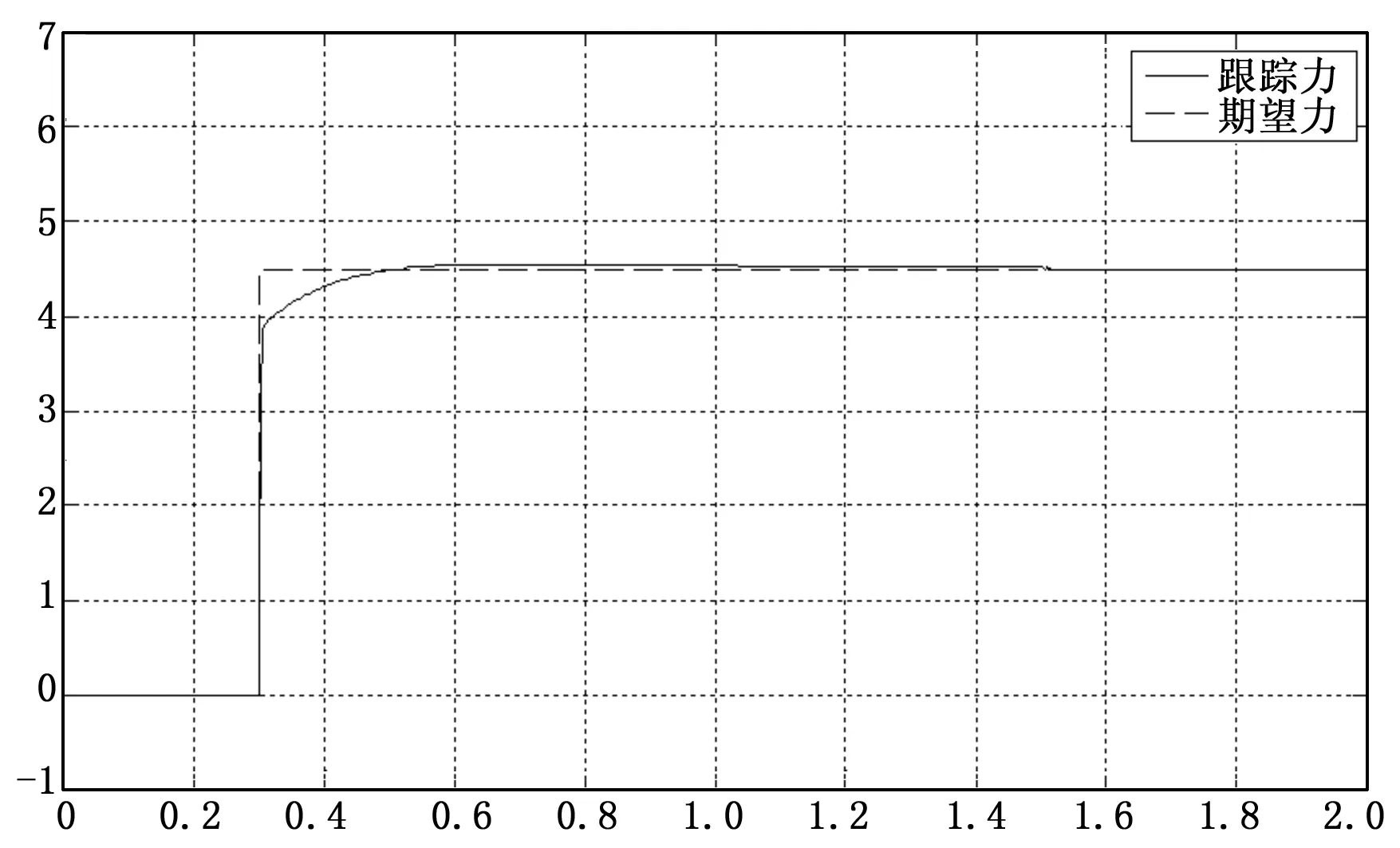
图8 PID参数的模糊自调整仿真
6 实验结果
实验采用华盛科技的6轴机械臂作为本体,将末端力控制系统安装在第6轴上。控制器采用TI公司的TMS320F28335型DSP。
实验设定接触时,末端力控制系统把力控制在4.5 N。图9是接触时DSP采集到的力反馈数据示意图。
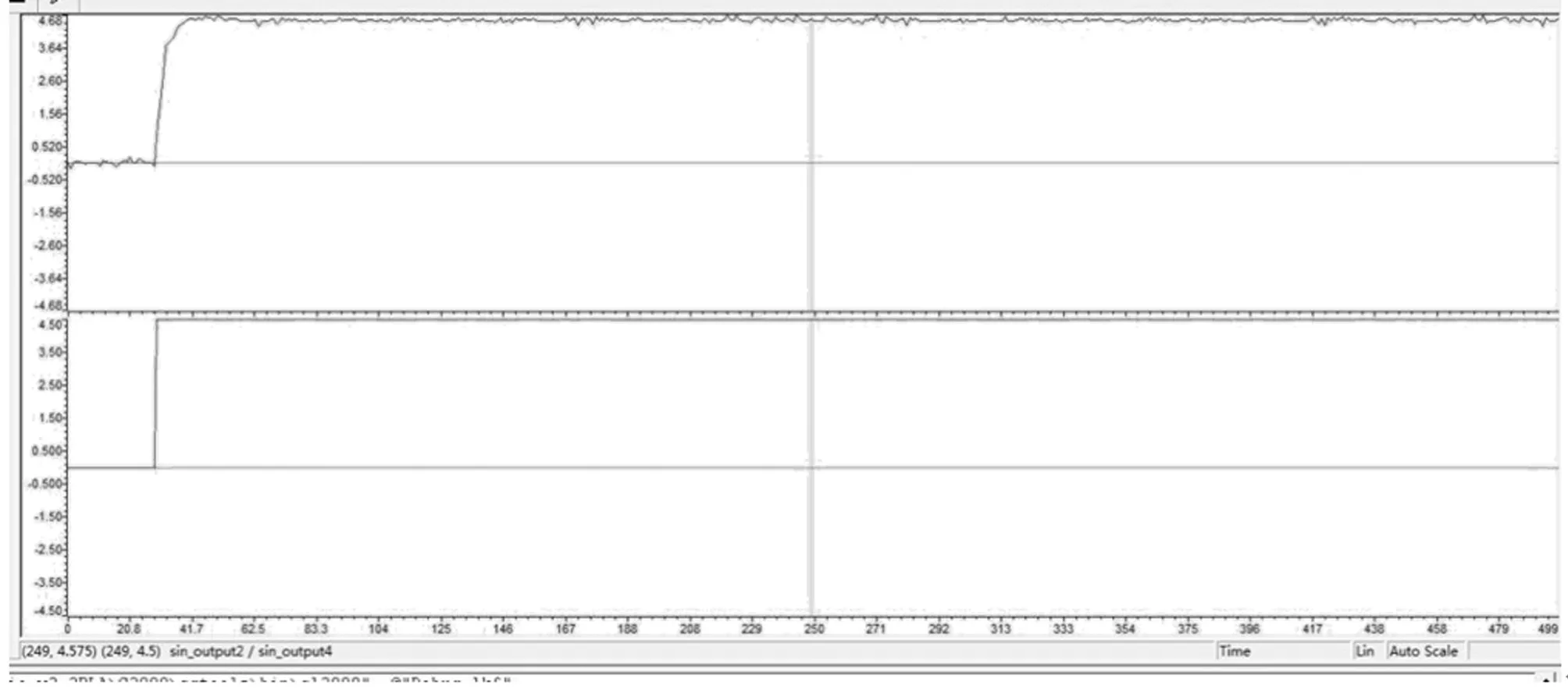
图9 接触时的力反馈值
7 结论
图10中,上面的图形是力反馈信号,下面的是期望的力信号。在碰撞发生之前,系统受力为零,处于不受约束的运动状态;在第30个采样周期左右时,碰撞发生。从上图可看出,系统没有发生明显振荡,但是出现少量超调,持续时间约40个采样周期;峰值约4.75 N,发生在第42个采样周期左右。之后经过20个采样周期,系统收敛并进入稳定状态,接触力保持在期望值4.5 N左右。上述实验结果与仿真结果接近,达到了预期效果。
[1] 毕 胜.国内外机械手发展现状[J].机械工程师,2008(7):5-8.
[2] 李晓燕.机械手力位置控制方法研究与应用[D].河北大学,2011.
[3] 盛国栋,曹其新,潘铁文,等.主从式机械手系统中力反馈的实现 [J].中国机械工程,2009,S2:106-111.
[4] 吴光文,王昌明,包建东,等. 基于自适应阈值函数的小波阈值去噪方法[J].电子与信息学报,2014(6):1340-1347.
[5] Le T H,Tamura Y,Matsumoto M.Spanwise pressure conherence on prisms using wavelet transform and spectral proper orthogonal decomposition based tools[J].Journal of Wind Engineering and Industrial Aerodynamics,2011,99(4):499-508.
[6] 周 尧,张丰华,田 沣,等.基于 Matlab 的圆柱螺旋弹簧设计计算与优化[J].设计与制造,2015,28(1):124-125.
Design of End Force Control System of Robot Based on DSP
Wang Zhi2, Wang Buyun2, Xu Dezhang2
(1.Wuhu Anpu Robot Industrial Technology Research Institute, Wuhu 241000,China;2.School of Mechanical and Automotive Engineering, Anhui Polytechnic University, Wuhu 241000,China)
The industrial robot motion can be divided into two different motion types of free motion and force- constrained motion. Not only the position of the force-constrained motion is controlled accurately, but also the contact force is controlled accurately. The paper studies the control system of end force of mechanical arm. High-precision electric sliding table is adopted as the actuator of the control system, and the flexible unit is added at the end of the electric sliding table, so that the drawback of system flexibility deficiency is overcome. The second order parameter of the system is determined based on the Lyapunov stability theory, and the stable adaptive design method proposed by Narendra is used to build the mathematical model of electric sliding table. The paper studies the design and algorithm of the soft system of the mechanical arm end. The influence of outside noise on the system is eliminated, the basic control strategy problem of force control is solved, and the response characteristics of the system is optimized when the system is controlled by force.
industrial mechanical arm; impedance control;force-constrained motion
2016-12-30;
2017-03-10。
安徽省科技攻关项目(1604a0902125);安徽省自然科学基金项目(1608085QF154);芜湖市科技计划项目(2016cxy03)。
王 志(1987-),男,安徽芜湖人,硕士研究生,主要从事运动控制系统分析与设计方向的研究。许徳章(1964-),男,安徽庐江县人,博士,教授,主要从事机器人信息感知,服务机器人与特种机器人方向的研究。
1671-4598(2017)08-0046-04
10.16526/j.cnki.11-4762/tp.2017.08.013
TP273
A
