SPH法切削破岩数值仿真

欧阳义平，杨启，2*，程旭东

（1.上海交通大学海洋工程国家重点实验室，高新船舶与深海开发装备协同创新中心，上海 200240；2.上海交大海洋水下工程科学研究院有限公司，上海 200231；3.中国铁建港航局集团有限公司，广东 珠海 519070）

SPH法切削破岩数值仿真

欧阳义平1，杨启1，2*，程旭东3

（1.上海交通大学海洋工程国家重点实验室，高新船舶与深海开发装备协同创新中心，上海 200240；2.上海交大海洋水下工程科学研究院有限公司，上海 200231；3.中国铁建港航局集团有限公司，广东 珠海 519070）

借助LS-DYNA计算软件，用SPH法求解偏微分方程进行切削破岩数值仿真，并以不同切削参数的切削破岩实验为原型进行计算，得出切削力与实验结果进行对比。数值仿真结果与实际相符，刀齿附近岩样单元应力和塑性应变均最大，切削过后岩样上形成切削槽，两侧存在破碎角，比以往数值仿真更接近实际情况，且破碎角大小与剪胀角有密切关系。大量仿真结果显示，计算所得切向力无论变化规律还是数值均与实验吻合较好，尤其是平均切向力，证实了SPH法仿真切削破岩的可行性，为切削破岩研究提供了一种新方法。

切削破岩；SPH法；LS-DYNA；数值仿真；切削力；破碎角

0 引言

切削破岩在隧道挖掘、航道和港口建设中有广泛应用。但切削破岩中岩石破碎机理复杂，切削力计算困难。通过实验方法研究其破碎机理虽然可靠，但成本太高。目前国内外越来越多学者通过数值仿真研究切削破岩。在切削破岩中使用的数值方法主要为有限元法和离散元法。Yu[1]和夏毅敏等[2]基于有限元法用LS-DYNA对切削破岩进行数值仿真。Su等[3]，Huang等[4]和 Van 等[5]用离散元法模拟切削破岩，并求得切削力。上述研究仍无法准确估计切削力和再现刀齿切削岩石破碎情况。近来SPH（Smoothed Particle Hydrodynamics）法在岩石破碎研究中有不少应用，且在研究受压作用下岩块破碎机理和破碎形态[6-8]，冲击破岩[9]，岩石坍塌[10]取得较好效果。Zhang等[11]和Li等[12]用SPH法仿真镐齿切削岩石，探讨了刀齿中应力峰值和岩石变形、失效情况，但均未涉及切削力。本研究借助LS-DYNA用SPH法对刀齿切削破岩进行数值仿真，重点分析该方法对切削力和破碎情况的预测能力，结合实验结果，探讨SPH法用于切削破岩研究的可行性。

1 计算方法

SPH法在天体物理学问题研究中诞生，目前越来越多应用于固体力学研究。该方法是一种无网格拉格朗日法，用于数值求解偏微分方程，其基础是插值理论[6-7，10]。无网格的特点使其能够处理许多不规则结构和复杂变形问题。其基本原理是：将几何体离散为许多具有一定体积和质量的粒子，以粒子取代单元；每个粒子携带了必要的物理量（如：密度、速度、压力和内能等），任意时刻，空间任意一点的物理量通过对该时刻临域内所有粒子插值求和得到，从而得到连续场的近似；最后用离散化的场函数求解偏微分方程。SPH法引入了核函数对场函数进行光滑，所得这种场的“近似”也叫场的核估计。场函数f在任意一点i的核估计＜f（xi）＞等于以点i为球心（圆心），2h为半径的球形（圆心）区域内所有粒子的场函数值插值的和（h为光滑长度），即，

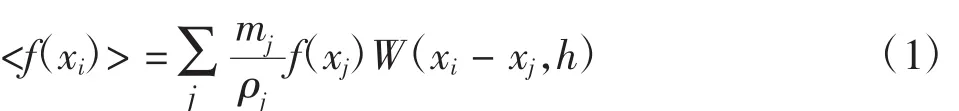
式中：xi为点i的位置坐标；xj为粒子j的位置坐标，均在空间固定坐标系下；f（xj）为粒子j处场函数的值；W为核函数，反映点的距离与贡献程度大小；h为光滑长度，通常与点i距离超过2h的粒子对点i的物理量无贡献，以xi为球心（圆心），2h为半径的球形（圆形）区域也称为点i的影响区域；j为落在点i影响区域内粒子的编号；mj为粒子j的质量；ρj为粒子j的密度。f在点i的微分形式的核估计为：

核函数W是光滑函数，可采用Monaghan[13]给出的三次样条函数。

假定岩石为连续介质，且在切削问题中不考虑重力，则质量和动量守恒方程的离散形式为：

式中：α、β表示坐标方向；vα为速度分量；σαβ为应力张量；∏ij为人工黏性，是为了使数值计算稳定而人为加入的项；δαβ是克罗内克函数，即α=β，δαβ=1，否则为0。为消除边界处单元缺失带来的计算误差，需要对方程（4）采用重整化修正，详见文献[8]和[14]。

2 数值仿真模型

本研究对刀齿切削硬石膏[15]进行数值仿真。原模型中岩样尺寸为0.5 m×0.5 m×0.3 m，岩样正方形面用胶水固定于切削平台上，切削速度为0.15 m/s，切削厚度1.5～7.5 mm。将岩样离散为间距1 mm的SPH单元，如果按照实际模型尺寸建模，并按实际速度切削，完成1 s切削，至少需要用1台普通4核台式计算机计算125万h。受限于计算机内存和计算能力，所取数值仿真模型尺寸比原模型小，如图1，为100 mm×50 mm×30 mm，切削速度提高为10 m/s，仿真时间缩减为0.003 s，该模型下，计算耗时7.5 h。刀齿切削方向平行于岩样上表面，且与岩样端面垂直。在LS-PrePost中建立计算模型，岩样单元间距为1 mm，刀齿划分为用六面体和八面体立体实体单元，单元最大边长为2 mm。岩样两个侧面和底面节点施加固定约束，限制6个自由度，其余面自由。刀齿做刚体平移，除沿着切削方向的平移运动外，其余自由度均被约束。

图1 数值仿真模型Fig.1 Numerical simulation model

岩样选用#173-Mohr-Coulomb材料模型，材料参数见表1[15]，其中岩样剪胀角大小根据文献[16]的研究，约为内摩擦角的一半。因岩石动力参数较难测得，因此本文所取均为准静态参数。刀齿选用#020-Rigid材料模型，密度为7 800 kg/m3，弹性模量为210 GPa，泊松比为0.3。

表1 岩样材料参数Table 1 Rock material parameters

在LS-DYNA的*Control中设置体积黏性和沙漏能控制，均按默认值设定。能量计算中将所有能量均包含在内，包括沙漏能和耗散能。*Control_SPH中设置计算区域为整个岩样区域和岩样正上方10 mm以内的区域。仿真时间为0.003 s，每隔5×10-6s进行1次采样，输出刀齿和岩样的相互作用力，岩样内部应力和应变。

3 仿真结果与分析

将LS-PrePost生成计算K文件导入LS-DYNA进行计算，再将结果导入LS-PrePost查看结果。得到的RCFORC文件可直接用MATLAB进行处理和绘图。

3.1 岩样的应力和塑性变形

用宽度为10 mm的刀齿切削岩样，切削厚度为4.5 mm，切削前角为20°。图2给出了数值仿真中t=0.001 5 s时刀齿齿尖附近岩样的等效应力和塑性变形，应力单位为MPa，图中未显示刀齿。图2（a）为过齿尖且垂直于切削方向所在截面的应力和刀齿对称面所在截面的应力。从图知，与刀齿刀刃接触的岩样单元应力最大，尤其是与刀齿两个齿尖接触的单元，随着与刀具距离的增加，岩样单元受到的应力值逐渐减小。随着切削推进，最大应力区域也不断向前移动，但刀齿附近岩样的应力分布情况基本相同。在边界附近的岩样单元应力值非常小，这说明岩样模型尺寸变小后与原模型差异不大，可以近似视为相同。图2（b）为与图2（a）相同截面上的塑性变形。切削中，与刀齿接触的岩样塑性变形很大，且这些单元的相邻单元的塑性变形也很大。刀齿向前切削，使其前方的岩样单元逐渐失效并将其从岩样上剥离，刀齿两侧和底部附近的岩样单元均有较大塑性变形，岩样被切削破坏。

图2 t=0.001 5 s时刀齿附近岩样的范式等效应力和塑性变形Fig.2 Von Mises stresses and plastic displacements of rock elements near the cutter in different moments at t=0.001 5 s

3.2 岩样破碎情况

刀齿切削过后，岩样上会留下一条切削槽，切削槽各垂直于切削方向的截面形状差异不大，且均有破碎角（breakout angle[15]）存在。图3给出了不同剪胀角下，仿真所得距离起始端面距离为5 mm处切削槽截面形状。从图可知，剪胀角越大，切削槽破碎角越明显（越大）。实际切削中，切削槽两侧均存在破碎角，但在此前的数值仿真均未提及。仿真中破碎角的出现能在现象上更接近实际，另外，它也改变了切削槽形状，当刀齿再次切削经过切削槽附近时，刀岩相互作用情况将与不存在破碎角时不同，进而影响后续切削，这恰好是实际应用中经常碰到的问题，因此将会有重要意义。

图3 不同剪胀角下切削槽形状Fig.3 Shape of grooves at different dilation angles

3.3 切削力

切削中刀齿与岩石的相互作用力为切削力，可视为切向力、法向力和侧向力的合力。由于仿真模型对称，侧向力理论上为零，实际仿真中侧向力相对于切向力和法向力也很小，不考虑。图4为切向力和法向力随时间变化曲线。从刀齿与岩样接触开始，切削力迅速增加，而后在一定范围内波动，与实际相符，但切削力波动幅度要比各自平均值小很多，这与实际有差异。

为便于将仿真结果与实验结果对比，求出切削力最大值和平均值。考虑到切削破岩中功耗主要受切向力影响，只对切向力进行分析。按照表2中的切削参数调整仿真模型，其余参数保持不变，得到仿真结果，并求得最大切向力和平均切向力，见表2。从表可知，仿真所得切向力与实验结果比较接近，平均切向力差异更小。

图4 切削力时历曲线Fig.4 Cutting force vs time

表2 切削力实验结果与数值仿真结果对比Table 2 Comparison of the experimental results and numerical simulation results of cutting forces

用最小二乘法将仿真与实验中所得切向力进行拟合，如图5，图中符号含义与表2相同。结果显示，数值仿真结果与实验有较高相关性，尤其是平均切向力。数值仿真结果普遍比实验结果大，结合表2可知，切削前角为-10°和0°时，数值仿真所得最大切向力要比实验值大；切削前角为10°和20°时吻合得非常好；切削前角为30°时，仿真结果比实验值略小。平均切向力随切削前角变化亦有类似规律，但不如前者明显。这可能是切削前角较小时，岩样在发生剪切失效之前已经存在其他形式失效，因此切向力无需达到剪切失效所需值。

图5 数值与实验切向力拟合Fig.5 Fitting of numerical and experimental tangential cutting forces

4 结语

1）借助LS-DYNA计算软件，用SPH法求解偏微分方程，进行刀齿切削破岩数值仿真，所得结果与实验结果较吻合。

2）在切削过程中，与刀齿接触的岩样单元受力和塑性应变均最大，随着离刀齿距离增加，应力和塑性应变均减小。最高应力区始终出现在刀齿前刃面附近，随着刀齿切削前进而移动。

3）切削过后，岩样上形成的切削槽两侧出现破碎角，比此前的类似仿真更接近实际情况。仿真结果显示，破碎角与剪胀角关系密切，剪胀角越大，破碎角越大。

4）数值仿真所得切削力时历曲线与实际比较吻合。所得平均切向力大小与实验值接近。

[1]YU B,KHAIR A W.Numerical modeling of rock ridge breakage in rotary cutting[C]//Rock mechanics:meeting society's challenges and demands.Proceedings of the 1 st Canada-US rock mechanics symposium.Vancouver,Canada:American Rock Mechanics Association,2007:519-526.

[2] 夏毅敏，薛静，周喜温.软岩切削过程的三维数值模拟[J].长安大学学报：自然科学版，2010，30（4）：102-106.XIA Yi-min,XUE Jing,ZHOU Xi-wen.3-D dimensional numerical simulation of soft rock cutting process[J].Journal of Chang′an University:Natural Science Edition,2010,30(4):102-106.

[3] SU O,AKCIN N.Numerical simulation of rock cutting using the discreteelementmethod[J].International Journal of Rock Mechanics and Mining Sciences,2011,48(3):434-442.

[4]HUANG H,LECAMPION B,DETOURNAY E,et al.Discrete element modeling of tool-rock interaction I:rock cutting[J].International Journal for Numerical and Analytical Methods in Geomechanics,2013,37(13):1 913-1 929.

[5] VAN WYK G,ELS D N J,AKDOGAN G,et al.Discrete element simulation of tribological interactions in rock cutting[J].International Journal of Rock Mechanics and Mining Sciences,2014,65(1):8-19.

[6]DAS R,CLEARY P W.Effect of rock shapes on brittle fracture using Smoothed Particle Hydrodynamics[J].Theoretical and Applied Fracture Mechanics,2010,53(1):47-60.

[7]MA G W,WANG X J,REN F.Numerical simulation of compressive failure of heterogeneous rock-like materials using SPH method[J].International Journal of Rock Mechanics and Mining Sciences,2011,48(3):353-363.

[8] TANG X W,ZHOU Y D,LIU Y L.Factors influencing quasistatic modeling of deformation and failure in rock-like solids by the Smoothed Particle Hydrodynamics method[J].Mathematical Problems in Engineering,2013(1):681-703.

[9]SHAH Q H,HAMDANI A.The damage of unconfined granite edge due to the impact of varying stiffness projectiles[J].International Journal of Impact Engineering,2013,59(1):11-17.

[10]KAREKAL S,DAS R,MOSSE L,et al.Application of a mesh-free continuum method for simulation of rock caving processes[J].International Journal of Rock Mechanics and Mining Sciences,2011,48(5):703-711.

[11]ZHANG Q,LI S J.Simulation study of the strength of pick based on LS-DYNA in different hardness of rock[J].Advanced Materials Research,2012,567(1):232-235.

[12]ZHAO L J,ZHOU Z H,GUAN Q Z,et al.Application of SPH in numerical simulation of roadheader hard rock cutting[J].Advanced Materials Research,2013,619(1):203-206.

[13]MONAGHAN J J,GINGOLD R A.Shock simulation by the particle method SPH[J].Journal of Computational Physics,1983,52(2):374-389.

[14]RANDLESPW,LIBERSKYLD.SmoothedParticleHydrodynamics:some recent improvements and applications[J].Computer Methods in Applied Mechanics and Engineering,1996,139(1-4):375.

[15]NUH Bilgin.Investigations into the mechanical cutting characteristics of some medium and high strength rocks[D].Newcastle Upon Tyne:University of Newcastle Upon Tyne,1977.

[16]ZHAO X G,CAI M.Influence of plastic shear strain and confinement-dependent rock dilation on rock failure and displacement near an excavation boundary[J].International Journal of Rock Mechanics and Mining Sciences,2010,47(5):723-738.

Numerical simulation of rock cutting using SPH method

OUYANG Yi-ping1,YANG Qi1,2*,CHENG Xu-dong3
（1.State Key Laboratory of Ocean Engineering,Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration,Shanghai Jiao Tong University,Shanghai 200240,China;2.Shanghai Jiao Tong University Underwater Engineering Institute Co.,Ltd.,Shanghai 200231,China;3.CRCC Harbour&Channel Engineering Bureau Group Co.,Ltd.,Zhuhai,Guangdong 519070,China）

Rock cutting of different cutting parameters were simulated by using SPH method to solve the partial differential equation with the help of LS-DYNA software,the rock cutting experiment with different cutting parameters is carried out as a prototype,and the cutting force is compared with the experimental results.The numerical results were in accord with the experimental results.The Von Mises stresses and plastic strains of those elements which contacted with the cutter were maximum.The cutting groove was formed on the rock sample after cutting,and there are breakout angles on both sides,which was much similar to the actual situation than former simulation results,and the size of the breakout angle is closely related to the dilatancy angle.A series simulation results show that the change law and the numerical value of the cutting force is in accord with the experiments,especially the mean tangential cutting forces.It is proved to be a suitable method that using SPH method to simulate rock cutting,and provides a new method for rock cutting research.

rock cutting;SPH mothed;LS-DYNA;numerical simulation;cutting force;breakout angle

U615.31；TU45；V448.253

A

2095-7874（2017）10-0013-05

10.7640/zggwjs201710003

2017-03-17

2017-05-23

国家自然科学基金项目（51179104）

欧阳义平（1987— ），男，湖南永州人，博士在读，主要从事船舶与海洋和疏浚设备研究。

*通讯作者：杨启，E-mail：yangqi110@sjtu.edu.cn