VSC-HVDC PI参数的系统级优化研究
2017-11-01李红日史迪锋
李 冲,袁 敏,李红日,史迪锋
(1.国网浙江省电力公司嘉兴供电公司,浙江 嘉兴 314033;2.嘉兴恒创电力设计研究院有限公司,浙江 嘉兴 314033)
VSC-HVDC PI参数的系统级优化研究
李 冲1,袁 敏2,李红日1,史迪锋1
(1.国网浙江省电力公司嘉兴供电公司,浙江 嘉兴 314033;2.嘉兴恒创电力设计研究院有限公司,浙江 嘉兴 314033)
以海上风电厂为代表的柔性直流输电系统近年来得到了大力发展。柔性直流输电系统包含整流侧和逆变侧以及直流输电线路,控制器参数的确定对整个系统都有很大影响,现阶段整流侧和逆变侧控制系统参数都是单独整定,因此无法得到系统级的最优参数。在直流输电线路等效模型基础上,建立了系统传递函数,根据时间乘绝对误差积分(ITAE)准则,利用粒子群算法进行了多目标下的系统级参数优化。仿真结果验证了系统传递函数以及优化算法的有效性和正确性。
柔性直流输电;解耦模型;参数优化;粒子群优化
0 引言
随着海上风电的迅速发展,其并网问题日益凸显,已成为制约海上风电发展的瓶颈之一。利用VSC-HVDC(柔性直流输电)可以有效实现海上风电的并网,改善系统运行特性及电能质量。因此,VSC-HVDC作为海上风电场并网的核心技术,已有了工程应用,其相应的控制、保护方案已较成熟。目前,国内外工程中VSC(电压源换流器)闭环控制系统基本都选用PI控制器[1],因此选取合适的PI控制器参数是确保系统获得良好特性的关键。
针对并网型VSC,目前国内外在HVDC的PI参数选择与整定方面的研究相对较少,在实际工程中,常采用试凑法或者经验法来整定PI参数,但这需要一定的技巧,且未必能得到满意的结果[2]。文献[3]通过试凑法结合经验调节天生桥—广州直流工程中的PI参数,并在PSCAD/EMTDC中进行了仿真验证,使系统满足动态响应的要求。文献[4]针对Simulink中的HVDC模型,提出了离线和在线2种优化PI控制器的方法,但由于此类方法没有考虑整流侧、逆变侧之间的相互影响,只是单纯地整定出每一端的PI参数,比较理想化,因此没有求得系统级的最优参数。
针对上述不足,以下对海上风电场VSC-HVDC系统,引入输电线路模型并研究了两侧换流器参数的联合优化问题。利用粒子群算法进行了多目标下的参数优化,通过仿真实验证明,优化后的参数具有更好的动态运行效果。
1 VSC控制系统模型
对于一个典型的VSC,通过解耦控制,有功功率Pc只与isd相关,无功功率Qc只与isq相关[5-8]。当只关心VSC-HVDC的外部输入-输出特性,忽略内环控制器的影响后,相应的简化解耦控制原理如图1所示。

图1 简化控制系统结构
VSC解耦整定模型构建后,其工作状态划分为有功功率类控制和无功功率类控制[9-12]。其中,典型有功类控制研究包括定有功功率控制,定直流电压控制;典型无功类控制研究包括定无功功率控制、定交流电压控制。
1.1 有功类整定模型
(1)定有功功率控制
图2为解耦后的定有功功率控制系统模型,其开环传递函数的表达式为:

其中: G0(s)=Kp+Ki/s ,
G1(s)=1/(1+3Tss) ,
G2(s)=(3/2)Usd,
G3(s)=1/(1+Tss) ,
式中: G0(s)为 PI控制环节; G1(s)为简化电流内环;G2(s)为 d 轴电流到有功功率的增益;G3(s)为反馈回路的时延;Ts为PWM(脉宽调制)整流器开关周期。

图2 定有功功率控制器的整定模型
(2)定直流电压控制
图3所示定直流电压控制器开环传递函数的表达式为:
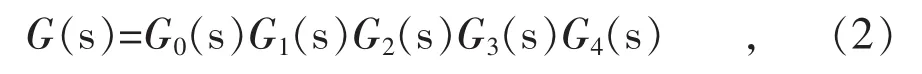
式中:G3(s)=1/sC为直流电流到直流电压的增益;其余环节同上文所述。
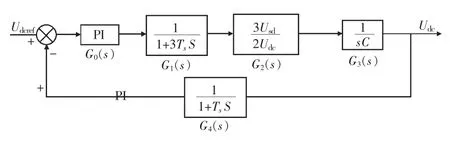
图3 定直流电压控制器的整定模型
1.2 无功类整定模型
(1)定无功功率控制
图4所示定无功功率控制器开环传递函数的表达式为:

式中:G2(s)为q轴电流到无功功率增益;其余环节同上文所述。

图4 定无功功率控制器的整定模型
(2)定交流电压控制
如图5所示定交流电压控制器开环传递函数的表达式为:
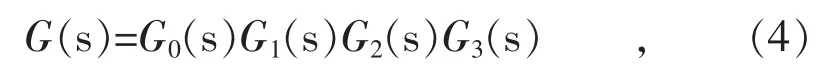
式中:G2(s)=Xs为交流系统内电抗;其余环节同上文所述。

图5 定交流电压控制器的整定模型
1.3 直流线路等效模型
直流线路∏型等效电路如图6所示[13]:
此直流线路为二端口网络,则频域下的Z参

图6 直流线路∏型等效电路
数方程为:
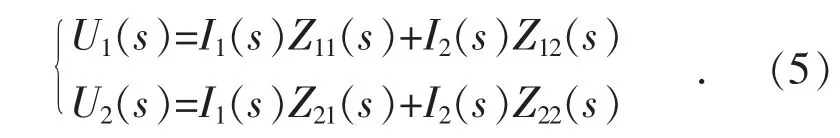
令式(5)中的 I2(s)=0,则:

进一步推导,得:

因此阻抗转移函数为:

1.4 系统级传递函数
VSC-HVDC系统由整流器、逆变器和直流线路组成。对于整流侧定有功功率、逆变侧定直流电压系统,在上述等效模型基础上,传递函数结构如图7所示,图中相关参数同上。

图7 定有功功率、定直流电压系统级传递函数
对于整流侧直流电流、逆变侧定直流电压系统,传递函数结构见图8,图中相关参数同上。
2 基于粒子群算法的系统级参数优化
PSO(粒子群优化)算法是一种新型的随机优

图8 定直流电流、定直流电压系统级传递函数

式中:fi为评估控制器操作性能的性能指标;ej(t)为第j个控制变量真实值和其参考值之间的误差;ωj为第j个控制变量的ITAE准则的权重因素,整流侧有功类控制变量和逆变侧有功类控制变量有着同等重要的地位,因此假定他们的权重系数一样,都为0.5。
以整流侧定有功功率、逆变侧定直流电压系化算法,由 Eberhart R.C博士和Kennedy J博士于1995年提出[14-15],该算法通过随机初始化一组值迭代搜寻最优值,目前已广泛应用于函数优化、数据挖掘、模糊系统控制及其他领域。
群体规模取50,维数为2,惯性因子w取1,加速因子c1=2,c2=2;最大迭代次数Tmax取60。具体步骤如下:
(1)初始化。初始化种群中所有粒子的位置和速度,通过随机方法把初始化的粒子位置和适应值设为最优值。
(2)根据粒子的位置,计算每个粒子的适应值。通过比较当代粒子的适应值和历史最优粒子的适应值,选取此次最优粒子。
(3)综合比较历史最小适应值粒子作为全局最优粒子,记录全局最优粒子位置。
(4)根据速度和位置更新方程,对粒子的速度和位置进行更新。
(5)如果达到终止条件,则迭代终止,输出算法的优化结果;如果没有达到终止条件,则继续迭代寻优。
对于一个VSC-HVDC系统,其包括多个控制回路,此时目标函数是最小化各个控制系统的ITAE(时间乘绝对误差积分)指标加权和,即:统为例,由解耦后的VSC整定模型,根据常用整定方法,可以得到PI控制器的初始参数,不再赘述。参照图7给出的系统级传递函数以及式(11)所示目标函数计算方法,根据初始值(直流线路电容值C为1 μF,等效电阻R为2 Ω)计算出控制回路目标函数,采用粒子群算法优化前后参数值如表1所示。

表1 优化前后PI控制器参数
3 仿真分析
整流侧和逆变侧三相交流相电压峰值310 V,等效电阻R均为0.5 Ω,L均为10 mH。直流线路电容值C均为1 μF,等效电阻R为2 Ω,开关频率f=27×50 Hz,仿真时间为3 s。
(1)逆变侧电压恒定,整流侧功率抬升实验。
由图9—16可知,在逆变侧直流电压参考值恒定的情况下,整流侧有功功率参考值1 s时由5 000 W抬升到6 200 W,优化后直流电压、有功功率、直流线路电压电流响应速度很快,为毫秒级,过冲和波动都不大,稳态精度高,超调量也在理想范围内,系统的各项性能指标都比较理想。

图9 整流侧定有功功率控制
(2)整流侧功率恒定,逆变侧电压抬升实验。
由图17—24可知,在整流侧有功功率参考值恒定的情况下,逆变侧直流电压参考值1 s时由500 V抬升到620 V,优化后的整流侧有功功率、相电压、相电流,逆变侧直流电压、相电压、相电流,以及直流线路电压电流响应比优化前速度更快,超调量更小,满足系统稳定性要求。

图10 整流侧交流a相电压

图11 整流侧交流a相电流

图12 送端直流线路电压

图13 受端直流线路电压

图14 逆变侧定直流电压控制

图15 逆变侧交流a相电压

图16 逆变侧交流a相电流
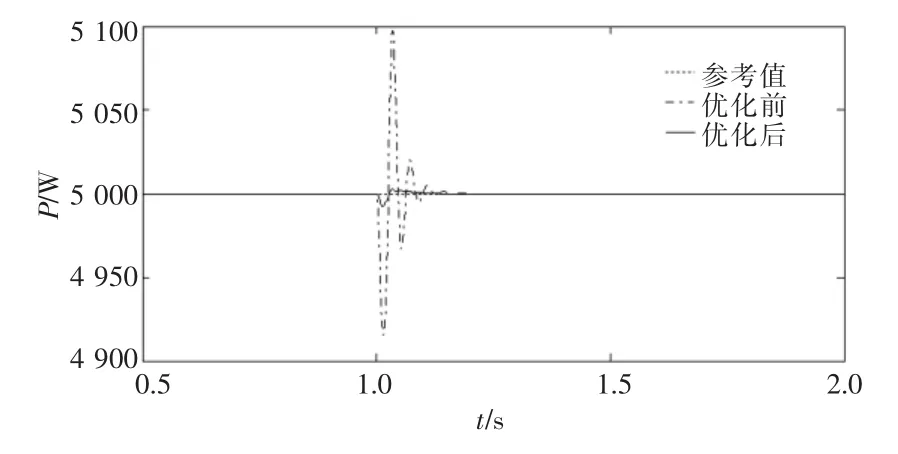
图17 整流侧定有功功率控制

图18 整流侧交流a相电压

图19 整流侧交流a相电流

图20 送端直流线路电压

图21 受端直流线路电压
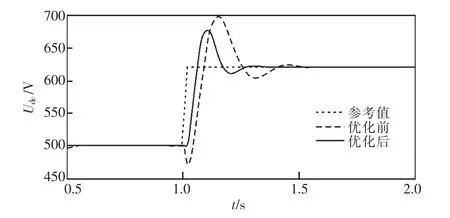
图22 逆变侧定直流电压控制

图23 逆变侧交流a相电压
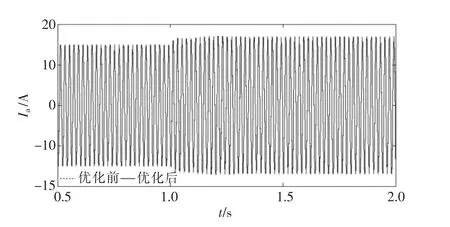
图24 逆变侧交流a相电流
4 结语
VSC-HVDC作为海上风电场并网输电的核心技术,已应用于实际工程,其相应的控制策略、保护策略已经成熟,研究选取合适的PI控制器参数是确保系统获得良好稳定性及动态响应特性的一个关键问题。
(1)VSC-HVDC系统包含整流侧和逆变侧,并且两侧有功相互影响,因此研究控制器参数的系统级优化很有必要。
(2)在VSC-HVDC控制系统模型以及直流线路模型的基础上,推导出了整流侧和逆变侧系统级传递函数。在ITAE准则下,根据粒子群算法对系统及参数进行了优化,仿真结果验证了系统模型及优化方法的有效性和准确性。
(3)提出的系统级传递函数及参数优化方法在理论以及仿真中得到了很好的证明,下一阶段可以在实际应用中进一步验证。
[1]DASH P K,ROOTRAY A,LIEW A C.Design of an energy function based Fuzzy tuning controller for HVDC links[J].Electrical Power and Energy Systems,1999,21(5)∶337-347.
[2]李伟.过程控制系统整定方法的研究[J].山东建筑工程学院学报,2003,18(1)∶63-67.
[3]JING YONG,REN ZHEN,OU KAIJIAN,et al.Parameter estimation of regulators in Tian-Guang HVDC transmission system based on PSCAD/EMTDC[C].Proceedings of 2002 International Conference on Power System Technology,Kunming,2002.
[4]李天云,刘智铭,党振宇,等.基于Simulink的HVDC PI控制器参数优化方法[J].电力自动化设备,2012,32(1)∶45-61.
[5]陈谦.新型多端直流输电系统的运行与控制[D].南京:东南大学,2004.
[6]姚为正,邓祥纯,易映萍,等.基于dq0同步坐标的柔性直流输电控制策略及仿真研究[J].电力系统保护与控制,2009,37(22)∶71-76.
[7]陈谦,李冲,金宇清,等.基于并网型VSC解耦模型的控制器参数优化[J].高电压技术,2014,40(8)∶2478-2484.
[8]张昕,杜俊杰,曾东,等.含VSC-HVDC系统的风光并网极限容量的研究[J].浙江电力,2016,35(12)∶64-68.
[9]汤广福.基于电压源换流器的高压直流输电技术[M].北京:中国电力出版社,2010.
[10]陈海荣,徐政.向无缘网络供电的VSC-HVDC系统的控制器设计[J].中国电机工程学报,2006,26(23)∶42-48.
[11]陈海荣,徐政.适用于VSC-MTDC系统的直流电压控制策略[J].电力自动化设备,2006,30(19)∶28-33.
[12]TAJJUDIN M,ADNAN R,ISHAK N,et al.Model reference input for an optimal PID tuning using PSO[C].Control System,Computing and Engineering (ICCSCE),2011 IEEE International Conference on.IEEE,2011.
[13]邱关源.电路[M].北京:高等教育出版社,2006.
[14]KENNEDY J,Eberhart R.Particle Swarm Opitimization[C].In∶IEEE Int 1 Conf on Neural Networks.Perth,Austraial,1995.
[15]阮立煜.基于粒子群算法的VSC-HVDC控制参数优化[J].浙江电力,2015,34(1)∶9-13.
下期要目
●智慧电厂与智能发电技术方向及关键技术综述
●即插即用就地化保护技术方案探讨
●储能型电动汽车充电站研究进展
●1 000 kV特高压变电站断路器失灵保护配置方案
●电阻抗扫描成像技术在变电站接地网故障诊断中的应用研究
●高压电缆缺陷模拟及状态评估技术评述
●变电站进线档导线不同步风摆动力学模型与分析
●源网荷用户400 V紧急切负荷控制实现
●能源互联网背景下的客户侧分布式电源综合运营服务平台及其关键技术研究
●融合配电自动化技术的海岛微电网控制策略研究及实现
Research on Combined Optimization of PI Parameters for VSC-HVDC
LI Chong1, YUAN Min2, LI Hongri1, SHI Difeng1
(1.State Grid Jiaxing Power Supply Company, Jiaxing Zhejiang 314033, China;2.Jiaxing Hengchuang Electric Power Design Institute Co., Ltd., Jiaxing Zhejiang 314033, China)
VSC-HVDC system such as offshore wind farm is widely used in recent years.VSC-HVDC system consists of rectifier side,inverter side and DC transmission lines.The determination of controller parameters has great impact on the whole system.Parameter settings of control system at rectifier side and inverter side are done separately,and thus the system-level optimal parameter can not be concluded.Based on the equivalent model of DC transmission lines,system transfer function is established.According to the integrated time absolute error criterion (ITAE), system-level parameter optimization under multiple objectives is conducted by particle swarm optimization.The simulation result shows that the system transfer function and optimization algorithm are effective and correct.
VSC-HVDC; decoupling model; parameter optimization; particle swarm optimization
10.19585/j.zjdl.201709007
1007-1881(2017)09-0033-06
TM46
A
2017-05-18
李 冲(1987),男,工程师,从事配电网运维工作。
(本文编辑:方明霞)
