A*算法的规模控制与代码实现

蒋晓南

摘要：A*算法是一种在静态路网中求解最短路径的最有效的方法，它是启发式搜索中最具代表性的一种，目前被广泛应用在机器人、自动控制、游戏等多个AI领域。然而A*算法会随着搜索规模的扩大而迅速降低搜索效率，所以有效控制A*搜索的规模才能让它适应更多场合。

关键词：A*算法；规模控制

中图分类号：TP393 文献标识码：A 文章编号：1009-3044（2017）22-0187-03

1概述

A*算法是一种在静态路网中求解最短路径最有效的方法。公式表示为：f（n）=g（n）+h（n），其中f（n）是从起点经由节点n到达终点的估价函数，g（n）是在状态空间中从起始节点到n节点的实际代价，h（n）是从n节点到目标节点的最佳路径的估计代价。能否找到最短路径的关键在于估价函数h（n）的选取，如果估价函数h（n）的值小于等于n到目标节点的距离实际值，这种情况下，搜索的点数多，搜索范围大，效率低，但能得到最优解。如果估价函数h（11）的值大于n到目标节点的距离实际值，这种情况下，搜索的点数少，搜索范围小，效率高，但不能保证得到最优解。

通过上段对A*算法的描述，可知A*算法会随着搜索规模的扩大而迅速降低搜索效率，只有有效控制A*搜索的规模才能让它适应更多场合。本文会首先介绍A*算法的基本思想，接着在讨论如何控制A*算法的规模，最后通过JAVA进行代码实现。

2A*算法的基本思想

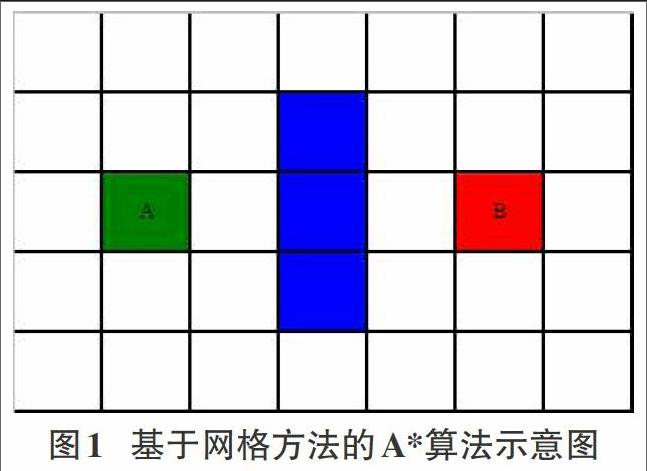
A*算法通常会将搜索区域分割成大小相同的网格，这是对搜索区域进行的有效简化。这样搜索区域就可以用一个简单的二维数组进行表示，数组中的一个元素就代表方格网中的一个方格。另外每个方格都必须被定义一个通过可能性的阀值，表示这个方格能否通过。接着，需要做的就是搜索从A到B需要经过的最短方格路径。如图1，左侧阴影方格A为起点，右侧阴影方格B为终点，中间三个阴影方格为障碍物。

A*算法的搜索过程依赖于“路径代价值”的估算，“路径代价值”的计算公式就是绪论中提到的：f（n）=g（n）+h（n），这里简单记为：F=G+H。

假定每次水平移动和竖直移动的代价为10，根据勾股定理，对角线的长度是两个直角边平方和的2次方根，因此对角的移动代价为14.14。为了简单起见，本文使用10和14。

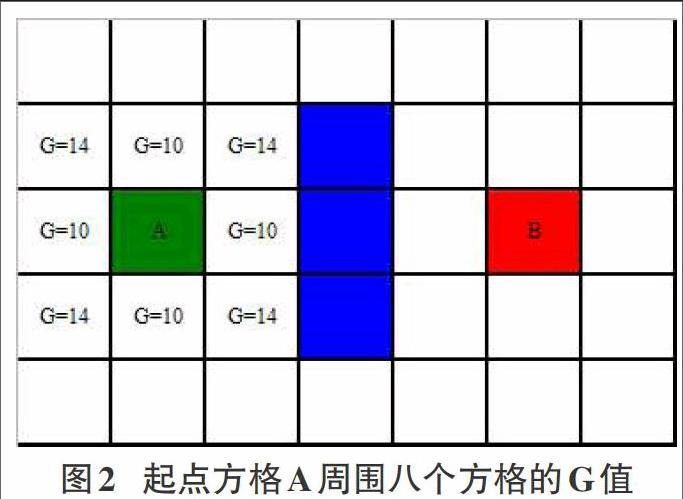
G是从起点A移动到给定方格的实际移动代价值。计算给定方格G值的方法是，用其移动路线中前一个方格的G值加上10或者14，分别对应水平竖直移动和对角线移动。那么，前一个方格的G值如何计算呢？不用担心，因为不断往前延伸，总会找到起点，而起点的G值是0。图2为起点方格A周围八个方格的G值。

H是从给定方格移动到终点B的预估移动代价值。之所以称为“预估”，是因为这只是一个猜测，它不考虑移动中可能遇到的障碍，只计算从给定方格水平或竖直移动到终点经过的方格总数，并忽略对角移动和障碍物，然后将方格总数乘上水平或竖直移动一格的代价值10，以得到H值。图3为起点方格A周围八个方格的H值。

F是从起点经由给定方格到达终点的综合代价值，即G和H的简单相加。图4为起点方格A周围八个方格的G、H、F值。

接下来A*算法会通过对F和G值的判断找到最短路径，但由于A*搜索过程复杂，本文不在这里赘述。

从图中不难看出，如果想让搜索到的路径更加精确，必须将方格划分的更小。然而这样一来方格数量就会激增，从而增加A*搜索的规模，降低搜索效率。那么，如何才能在满足应用要求的情况下，降低搜索规模呢，这是本文下面要讨论的内容。

3A*算法規模控制

实际应用中，目标往往只出现在某些固定的点，不会毫无规律；又或是应用本身对精度要求并不高，只需要找到目标所在区域即可。基于这样的思路，作者提出两个降低搜索规模的可行方案。

如图5所示，传统方法会将搜索区域进行这样的划分，并进行A*搜索。本文下面以这张图举例分析如何降低搜索规模。

节点网：

如图6所示，如果目标只会出现在图中小圆点位置，那完全没有必要将图划分成那么多方格，只要将节点连接起来形成一张节点网，就可以使用A*算法找到这些点之间的最短连接路径。

节点网和传统网格方法的本质是一样的，它们都是对算法难以操作的状态空间进行简化，但是节点网比传统网格方法存储代价低得多，但缺点是不能很好地适应动态障碍。对于这个问题，较好的解决方法是在节点网中融合进避障系统，利用避障系统来对付移动障碍，利用节点网来实现在地图中的常规穿行，这样即使在常规行进的路线上出现障碍物，壁障系统也能帮忙躲开它。

区域网：

如图7所示，搜索区域被划分成几个多边形区域，如果对搜索精度要求不高，只需要确定目标在某个区域，那么就可以使用这种区域网。设计时可以把多边形区域的中心点作为节点，从而形成节点网。

区域网具有节点网的大多数优点，而且更加节省存储空间，但必须使用避障系统，而且如果构建区域网的方法本身不够智能，那么就会出现一些看起来非常奇怪的路径。

避障系统：

本文前面提到的避障系统，是一种利用磁铁同性相斥原理设计出来的避开障碍物的系统。

简单得说，就是当探路者根据A*算法搜索出来的最佳路径行进时，突然遇到移动障碍物，或是因为路径计算不够精确而与障碍物有碰擦的危险，就对探路者施加一个反作用力，距离越近反作用力越强，好像同极性的两块磁铁，以此来避开障碍物。有了它，节点网和区域网就有了用武之地。

4代码实现

由于本设计是用JAVA语言进行程序实现与测试，因此以下给出的均为JAVA源代码。

节点网和区域网中都牵涉到节点问题，所以节点的设计尤为关键。

以下是“节点”类的成员变量和重要成员函数：

classNode{

private Node parentNode；//父节点，此变量非常重要，是获得最佳路径的线索

private Stringid；//为了便于测试，加人一个节点id，作为将来的输出显示

private boolean attainability；//节点是否可通过

private int X，Y；//节点的位置信息

private int G；//当前点到起点的移动耗费

private int H；//当前点到终点的移动耗费

privateint F；//f=g+h

public Node[]getNeighborNodes（Node[][]map）{…}//获得周围节点

publicintgetNeighborNodeCostG（Node neighborNode）{…}//获得相邻节点G值

public void costGHF（Node endNode）{…}//计算当前节点GHF值

getNeighborNodes函数用于获得当前节点周围的节点，并自动给无效的节点作出标记（即给无效节点赋值null）。入口参数为一个Node类型的二维数组，返回一个Node类型的一维数组。

getNeighborNodeCostG函数用于获得当前节点的相邻节点的G值。人口参数为一个相邻节点，返回一个整型的G值。

costGHF函数用于计算当前节点的GHF值。入口参数为A*搜索的终点，无返回类型。

以下是“寻路”类的成员变量和重要成员函数：

public class PathFinding{

private intnodeMapRow；//节点地图行数

private intnodeMapColumn；//节点地图列数

private Node[][]nodeMap；//地图数组

private Node startNode；//起点

private Node endNode；//终点

private Stack open；//开启列表

private Stack close；//关闭列表

private Node getMinCostNode（Stack s）{…}//获得最小代价节点

private void Astar（）{…}//A*算法

public

Stack

getPath（intstartX，intstartY，intendX，intendY）{…}//获得最佳路径

public

void printPathontstartX，intstartY，intendX，intendY）{…}//打印最佳路径

getMinCostNode函数用于从提供的开放列表中获得最小代价值节点，同时将其从开放列表中删除。函数入口参数为一个堆栈类型的开放列表，返回一个最小代价的节点。

Astar函数用于A*搜索，是本文最核心的函数之一。此函数既无人口参数也无返回类型，原因在于很多准备工作已在其他类和函数中完成。

getPath函数用于获得A*算法搜索出的路径节点。入口参数为起点和终点的X、Y坐标，返回的路径节点用堆栈存储。

printPath函数用于打印getPath获得的最佳路径。入口参数为起点和终点的X、Y坐标，无返回类型。此函数在A*搜索中并不起任何作用，只是为了测试A*搜索而编写的。

5结论

测试结果：

图8和图9，是使用本设计之前和之后针对同一个搜素区域进行1000次循环搜索的对比。采用本设计后的搜索时间只有传统方式的1/5，显然大大缩减了搜索时间，提高了搜索效率。需要指出的是，本设計虽然有效降低的搜索规模，但并非适用于所有场合。至于所适用的场合在前文中已有讨论，不在此赘述。