疲劳荷载作用下的三维弹塑性弯曲裂纹尖端张开位移

杨大鹏，潘海洋，刘邦先，张平萍，杨新华

(1.中钢集团郑州金属制品研究院有限公司，河南 郑州，450001；2.华中科技大学土木工程与力学学院，湖北 武汉，430074；3.郑州职业技术学院机械工程系，河南 郑州，450121；4.郑州职业技术学院城市轨道交通系，河南 郑州，450121)

疲劳荷载作用下的三维弹塑性弯曲裂纹尖端张开位移

杨大鹏1,2,3，潘海洋4，刘邦先3，张平萍1，杨新华2

(1.中钢集团郑州金属制品研究院有限公司，河南 郑州，450001；2.华中科技大学土木工程与力学学院，湖北 武汉，430074；3.郑州职业技术学院机械工程系，河南 郑州，450121；4.郑州职业技术学院城市轨道交通系，河南 郑州，450121)

综合考虑疲劳作用应力、三维塑性区域边界上的交变正应力与交变剪应力，利用二阶摄动方法建立了计算疲劳载荷作用下三维弹塑性弯曲裂纹尖端张开位移的理论模型。用数值解法进行求解，并作图分析了三维弹塑性弯曲裂纹尖端张开位移的最大值和变化幅值与三维裂纹体几何尺寸及外载荷之间的变化关系。结果表明，随着裂纹体厚度的增大，三维弹塑性弯曲裂纹尖端张开位移的最大值与变化幅值不断减小；当裂纹体几何尺寸相同时，弯曲裂纹尖端张开位移的最大值与变化幅值均随外载荷的增加而逐渐增大。

三维裂纹体；弯曲裂纹；张开位移；疲劳荷载；二阶摄动方法

目前关于弯曲裂纹扩展路径的研究大多局限于二维线弹性断裂和二维弹塑性断裂问题[1-7]，而针对疲劳载荷作用下三维裂纹体弹塑性弯曲裂纹的路径预测、三维裂纹体弹塑性弯曲裂纹尖端塑性区域交变应力场的计算、张开位移最大值与变化幅值的确定等问题的研究相对缺乏。在工程实际中，裂纹体材料的厚度通常是不可忽略的，而且往往比较大。因此，研究三维疲劳弹塑性弯曲裂纹的断裂特性是非常有必要的。本文将运用二阶摄动方法计算出疲劳载荷作用下三维弹塑性弯曲裂纹尖端张开位移的最大值与变化幅值，从而更精确地服务于工程实际。

1 相关符号与说明

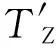
αZ、βZ、γZ为三维弯曲裂纹的形状参数，kIZ、kIIZ、bIZ、bIIZ、TZ是与二维弯曲裂纹相对应的三维弯曲裂纹断裂特性参量；HZ为三维弯曲裂纹以及塑性裂纹的直线部分的长度,RZ为三维弯曲裂纹尖端塑性区在裂纹直线部分延长线上的射影长度，RZ可以根据文献[11-13]提供的思路、方法与力学模型求解，aZ为三维弯曲裂纹于裂纹直线部分延长线上的投影长度，令cZ=RZ+aZ，δZ为三维弯曲延伸裂纹尖端张开位移。弯曲裂纹尖端场的奇异性特征严重依赖于材料的本构类型，本文中的材料本构是理想塑性的。

2 三维疲劳弯曲裂纹尖端张开位移的确定

本文采用经过拓展的弯曲裂纹Dugdale模型计算三维疲劳弯曲裂纹尖端张开位移，这个拓展模型的合理性已经在文献[13]中得到证明。根据文献[11-13]，可得如下关系式：

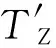
exp[-B1(z/B)(r/B)B2(z/B)]

(1)

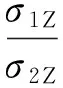
(2)

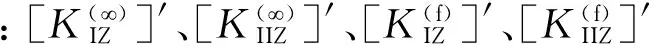
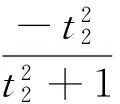
(3)

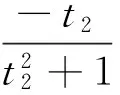
(4)

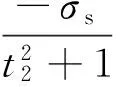
(5)

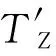
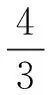
(6)

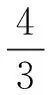
(7)

(8)

(9)

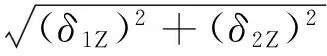
(10)

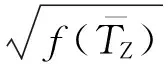
(11)

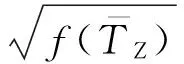
(12)

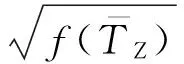
(13)

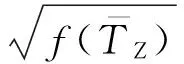
(14)

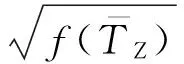
(15)

式(11)～式(15)中：kI、kII为应力强度因子；bI、bII、T均为系数，取决于裂纹弯曲延伸扩展之前的边界值问题的解。

同时，可以确定疲劳载荷作用下某一时刻三维弯曲裂纹尖端I型张开位移δ1Z、II型张开位移δ2Z的大小：

(16)

(17)

在疲劳荷载作用下，裂纹尖端塑性区的大小呈交替性变化，三维弯曲裂纹张开位移的周期变化是由于kIZ、kIIZ、bIZ、bIIZ、TZ、RZ等参量的循环增减而引起的，于是可用下列简化函数式表达:

δ1Z=δ1Z(αZ,βZ,γZ,aZ,t2,σs,kIZ,

kIIZ,bIZ,bIIZ,TZ,RZ)

(18)

(δ1Z)max=δ1Z[αZ,βZ,γZ,aZ,t2,σs,(kIZ)max,

(kIIZ)max,(bIZ)max,(bIIZ)max,(TZ)max,(RZ)max]

(19)

(δ1Z)min=δ1Z[αZ,βZ,γZ,aZ,t2,σs,(kIZ)min,

(kIIZ)min,(bIZ)min,(bIIZ)min,(TZ)min,(RZ)min]

(20)

δ2Z=δ2Z(αZ,βZ,γZ,aZ,t2,σs,kIZ,

kIIZ,bIZ,bIIZ,TZ,RZ)

(21)

(δ2Z)max=δ2Z[αZ,βZ,γZ,aZ,t2,σs,(kIZ)max,

(kIIZ)max,(bIZ)max,(bIIZ)max,(TZ)max,(RZ)max]

(22)

(δ2Z)min=δ2Z[αZ,βZ,γZ,aZ,t2,σs,(kIZ)min,

(kIIZ)min,(bIZ)min,(bIIZ)min,(TZ)min,(RZ)min]

(23)

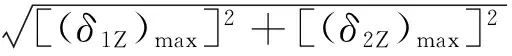
(24)

(25)

ΔδZ=(δZ)max-(δZ)min

(26)

3 三维疲劳弯曲裂纹尖端张开位移最大值与变化幅值的计算与分析

下面以碳钢为例，根据上述公式用数值解法计算材料三维弹塑性弯曲裂纹尖端张开位移，研究张开位移的最大值和变化幅值与三维裂纹体几何尺寸及外载荷之间的变化关系。碳钢的泊松比ν=0.25，屈服极限σs=1725 MPa, 弹性模量E=2.15×105MPa。

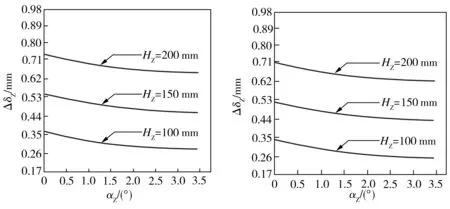
当垂直于初始直线裂纹方向的外应力σaZ=0.5σs、平行于初始裂纹方向的外应力σrZ=0.1σs、σZ=50 mm时，三维弯曲裂纹尖端张开位移的最大值随裂纹形参αZ的变化关系如图1所示。当σaZ=0.33σs、σrZ=0.03σs、aZ=50 mm时，三维弯曲裂纹尖端张开位移的变化幅值随裂纹形参αZ的变化关系如图2所示。

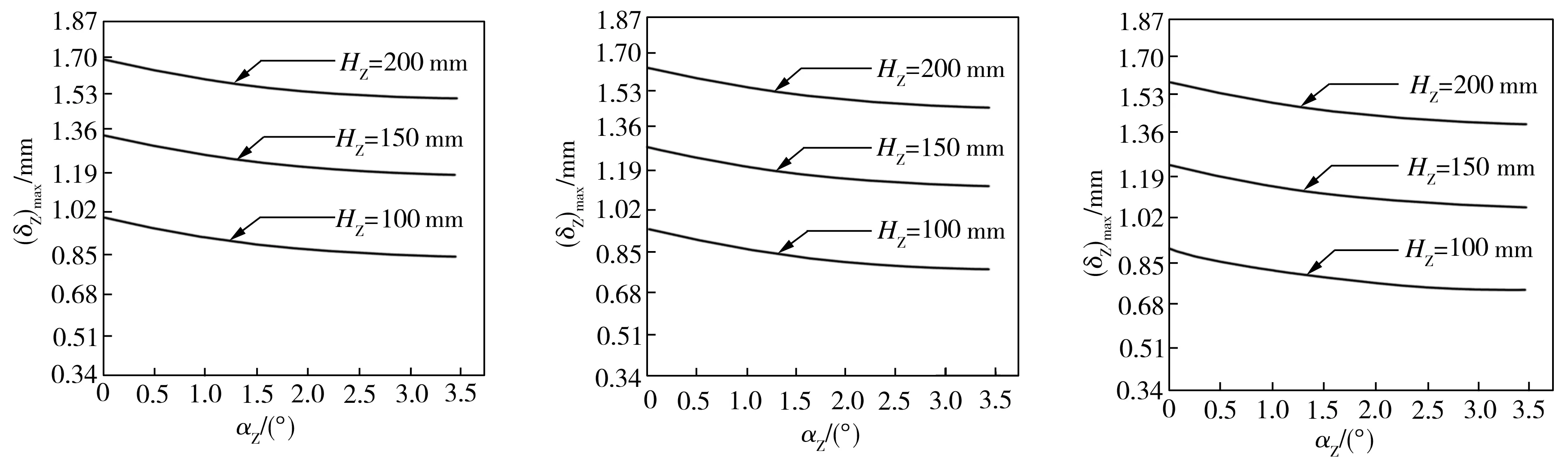
(a)B=10 mm (b)B=20 mm (c)B=30 mm

(d)B=50 mm (e)B=100 mm

图1三维弯曲裂纹尖端张开位移的最大值随裂纹形参αZ的变化(σaZ=0.5σs,σrZ=0.1σs，aZ=50mm)

Fig.1Variationofthemaximumof3DcurvedcracktipopeningdisplacementwiththecrackshapeparameterαZ(σaZ=0.5σs,σrZ=0.1σs，aZ=50mm)

从图1、图2可以看出，在同样的外载荷作用下，相同的三维裂纹直线部分长度对应的弯曲裂纹尖端张开位移的最大值与变化幅值随着三维裂纹形状参数αZ的不断增大而减小。另外，在外载荷、三维裂纹直线部分长度HZ和三维弯曲裂纹形状参数αZ相同的条件下，当三维裂纹体厚度逐渐增加时，裂纹尖端张开位移的最大值与变化幅值均不断减小。

三维弯曲裂纹尖端张开位移的最大值和变化幅值随外载荷(用垂直于初始直线裂纹方向外应力的最大值(σaZ)max及其变化值ΔσaZ与屈服极限σs的比值来表征)的变化分别如图3和图4所示。

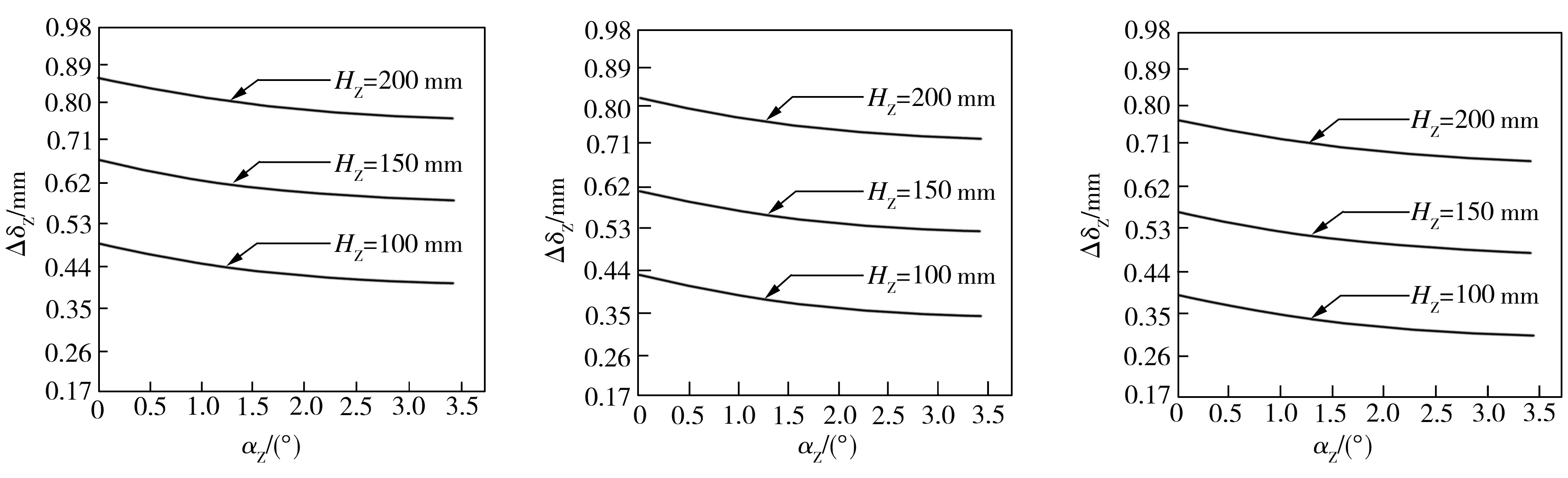
(a)B=10 mm (b)B=20 mm (c)B=30 mm

(d)B=50 mm (e)B=100 mm

图2三维弯曲裂纹尖端张开位移的变化幅值随裂纹形参αZ的变化(σaZ=0.33σs,σrZ=0.03σs，aZ=50mm)

Fig.2Variationoftheamplitudeof3DcurvedcracktipopeningdisplacementwiththecrackshapeparameterαZ(σaZ=0.33σs,σrZ=0.03σs，aZ=50mm)

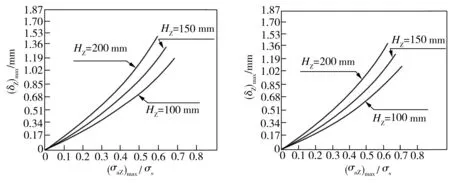
(a)B=10 mm (b)B=20 mm

图3三维弯曲裂纹尖端张开位移的最大值随外载荷的变化(aZ=50mm,αZ=0.5°)

Fig.3Variationofthemaximumof3Dcurvedcracktipopeningdisplacementwiththeexternalload(aZ=50mm,αZ=0.5°)

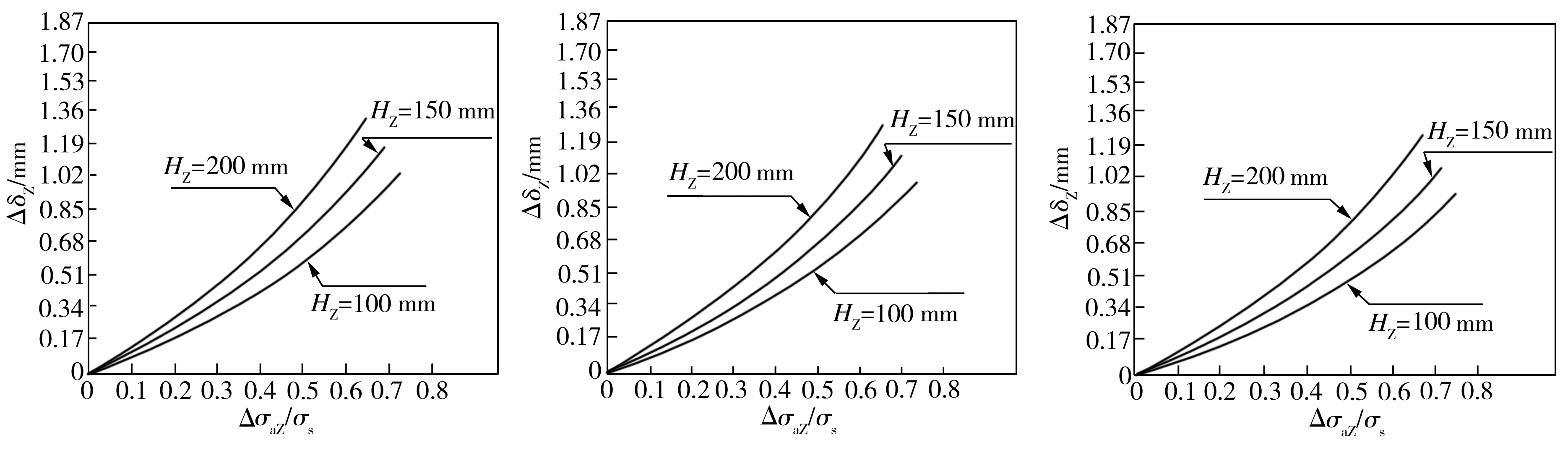
(a)B=30 mm (b)B=50 mm (c)B=100 mm

图4三维弯曲裂纹尖端张开位移的变化幅值随外载荷的变化(aZ=50mm,αZ=0.5° )

Fig.4Variationoftheamplitudeof3Dcurvedcracktipopeningdisplacementwiththeexternalload(aZ=50mm,αZ=0.5° )

从图3、图4可以看出，当三维裂纹体厚度和裂纹直线部分长度相同时，三维弯曲裂纹尖端张开位移的最大值与疲劳载荷最大值正相关，其变化幅值与疲劳载荷变化幅值正相关。另外,随着三维裂纹体厚度的增加，对于相同的裂纹直线部分长度和弯曲程度，三维弯曲裂纹尖端张开位移的最大值随疲劳载荷最大值的提高而不断增大的速度逐渐降低，其变化幅值随疲劳载荷变化幅值的提高而不断增大的速度也逐渐降低。

4 三维疲劳弹塑性弯曲裂纹扩展的判据

根据文献[11-13]可以得到：

(1)疲劳载荷作用下，三维弯曲裂纹的扩展速率为

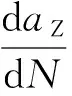
(27)

式中：R为应力比，即R=(σZ)min/(σZ)max；N为疲劳荷载的循环次数；C′、m′均为材料常数；δCZ为三维弯曲裂纹的断裂韧性；ΔδthZ为三维弯曲裂纹张开位移变化幅度的门槛值。

(2)三维疲劳弹塑性弯曲裂纹在远场交变应力作用下稳定存在的条件为

ΔδZ<ΔδthZ

(28)

(3)三维疲劳弹塑性弯曲裂纹在远场交变应力作用下稳定扩展的条件为

ΔδZ≥ΔδthZ，且(δZ)max<δCZ

(29)

(4)三维疲劳弹塑性弯曲裂纹在远场交变应力作用下失稳扩展的条件为

ΔδZ≥ΔδthZ，且(δZ)max≥δCZ

(30)

5 结语

本文运用二阶摄动方法得出三维弹塑性弯曲裂纹尖端张开位移的最大值与变化幅值计算公式，作图分析了三维弹塑性弯曲裂纹尖端张开位移的最大值、变化幅值与三维裂纹体厚度、裂纹直线部分长度、裂纹形状参数以及外载荷之间的关系，并进一步讨论了三维疲劳弹塑性弯曲裂纹扩展的判据。由于三维疲劳弹塑性弯曲裂纹在土木建筑、航空航天、舰船潜艇等工程结构中普遍存在，因此本研究具有重要的理论意义和工程实用价值。

[1] 黄学伟，蔡力勋，包陈，等.基于低周疲劳损伤的裂纹扩展行为数值模拟新方法[J].工程力学, 2011，28(10):202-208.

[2] 廖芳芳，王伟，陈以一.往复荷载下钢结构节点的超低周疲劳断裂预测[J].同济大学学报：自然科学版，2014，42(4)：539-547.

[3] 嵇醒.断裂力学判据的评述[J].力学学报, 2016，48(4)：741-753.

[4] 王清远，刘永杰.结构金属材料超高周疲劳破坏行为[J].固体力学学报, 2010,31(5):496-503.

[5] 魏国前，岳旭东，党章，等.结合S-N曲线和断裂力学的焊接结构疲劳寿命分析[J].焊接学报,2017，38(2):23-27.

[6] Zhao Minghao, Dang Huayang, Xu Guangtao, et al. Dielectric breakdown model for an electrically semi-permeable penny-shaped crack in three-dimensional piezoelectric media[J]. Acta Mechanica Solida Sinica, 2016,29(5):536-546.

[7] Yang Shengqi, Huang Yanhua, Ranjith P G, et al. Discrete element modeling on the crack evolution behavior of brittle sandstone containing three fissures under uniaxial compression[J].Acta Mechanica Sinica, 2015,31(6):871-889.

[8] 丁遂栋,孙利民.断裂力学[M].北京：机械工业出版社,1997:148-169.

[9] 杨卫.宏微观断裂力学[M].北京：国防工业出版社,1995：65-70.

[10] 杨大鹏,赵耀,白玲.准静载作用下弹塑性微弯裂纹尖端塑性区[J].应用力学学报,2010,27(2): 401-405.

[11] 郭万林，于培师.构件三维断裂与疲劳力学及其在航空工程中的应用[J].固体力学学报，2010，31(5):553-571.

[12] 张斌.材料结构宏观三维断裂和微观破坏行为研究[D].南京：南京航空航天大学，2005.

[13] 杨大鹏.微弯延伸裂纹断裂特性的研究[D].武汉：华中科技大学，2006.

Threedimensionalelastic-plasticcurvedcracktipopeningdisplacementunderfatigueload

YangDapeng1,2,3,PanHaiyang4,LiuBangxian3,ZhangPingping1,YangXinhua2

(1.Sinosteel Zhengzhou Research Institute of Steel Wire Products Co., Ltd., Zhengzhou 450001, China; 2.School of Civil Engineering and Mechanics, Huazhong University of Science and Technology, Wuhan 430074, China; 3.Department of Mechanical Engineering, Zhengzhou Technical College, Zhengzhou 450121, China; 4.Urban Rail Transport Department, Zhengzhou Technical College, Zhengzhou 450121, China)

Taking the effects of fatigue stress, cyclic normal and shear stresses on the boundaries of three dimensional plastic area into consideration, this paper has built the theoretical models to calculate three dimensional elastic-plastic curved crack tip opening displacement (CCTOD) under fatigue loads by using second order perturbation method. Numerical solutions were made，and the relation curves between the maximum or amplitude of CCTOD and the crack body geometrical dimensions as well as the external loads were analyzed. The results show that the maximum and amplitude of CCTOD decline with the increase of crack body thickness. When crack bodies have the same size, the maximum and amplitude of CCTOD increase with increasing external loads.

three dimensional crack body; curved crack; opening displacement; fatigue load; second order perturbation method

2017-04-10

国家自然科学基金重大研究计划项目(91016026)；河南省博士后科研资助项目(博士后编号：166053).

杨大鹏(1976-)，男，中钢集团郑州金属制品研究院有限公司博士后工作站以及华中科技大学土木工程与力学学院力学系博士后流动站研究人员，郑州职业技术学院副教授.E-mail: ydpzpysh@163.com

10.3969/j.issn.1674-3644.2017.05.014

TB301

A

1674-3644(2017)05-0395-06

[责任编辑尚晶]