基于自适应占空比扰动法的光伏并网系统仿真分析研究

郑俊观 王硕禾

（石家庄铁道大学电气与电子工程学院 河北石家庄 050043）

基于自适应占空比扰动法的光伏并网系统仿真分析研究

郑俊观 王硕禾

（石家庄铁道大学电气与电子工程学院 河北石家庄 050043）

由于光伏组件输出特性具有明显的非线性，研究中需要根据光伏组件的工程模型建立其通用仿真模型。本文在对经典占空比扰动法进行深入分析的基础上，提出了一种自适应占空比扰动法；同时，利用双闭环控制方法对光伏系统的逆变进行控制；最后，通过对光伏阵列、自适应占空比扰动算法和逆变进行仿真，仿真分析结果表明，所建立的光伏阵列模型能够较好的模拟光伏阵列的特性；所提出自适应占空比扰动法，在一定程度上弥补了扰动法的不足；逆变输出的电流与电网的电压同频同相，达到了并网的要求。

光伏并网系统 光伏阵列 自适应占空比扰动法 双闭环控制

随着能源短缺和环境问题日益严峻，新能源的研究和开发受到了各国的广泛关注。在新能源发电中，光伏发电因具有清洁、零污染、无噪声、适用地域广等特点备受青睐[1]。光伏组件是由多个光伏电池串并联而成，分析和建模具有一定困难，同时，如何根据光伏组件厂家提供的在标准条件下光伏组件4个特性参数（Uoc、Isc、Im、Um）来建立仿真模型，是光伏组件建模需要重要思考的问题之一[2]。为了实现光伏组件输出功率最大，需要采用最大功率跟踪技术。目前比较常用MPPT算法有恒定电压法、扰动观察法和电导增量法，每种算法都有各自的优缺点[2-3]，另外，为了提高系统的鲁棒性，一些学者把智能算法引进到了MPPT算法中，比如人工神经网络控制、模糊控制等[4]。为了把光伏组件逆变成与电网电压同频同相的高质量正弦波的交流电流，通常对逆变器输出侧的电流进行控制，控制方法有双闭环控制、重复控制、滑模控制、无差拍控制等，其中最常用的是双闭环控制[5]，由于光伏逆变器与有源滤波器在结构上有许多相似之处，一些学者提出了光伏并网与有源滤波统一控制的策略[6]。

本文分别从改进MPPT算法和并网控制策略2个方面进行研究。在光伏组件仿真模型的基础上，重点分析了占空比扰动法，针对该算法的不足，在其基础上提出了用可变步长kdU/dP来代替定步长的方案，其中，K为常数，通过仿真证明了改进的MPPT算法能过弥补扰动法的不足。光伏的逆变控制采用改进的双闭环控制，外环为电压环，内环为电流环，为了消除电网电压波动造成的损耗，引入其电压的前馈环节。在上述方案下，通过搭建光伏并网系统仿真模型，仿真结果证明了该控制方法能够达到并网要求。

1 主电路拓扑结构

本文中光伏并网系统主电路的拓扑结构为两级式，前级DC/DC环节完成升压和最大功率点跟踪，后级DC/AC环节完成逆变，使输出的电流与电网的电压同频同相，功率因数为1。将最大功率点跟踪和逆变器的控制分开，实现控制相对容易，效率较高。

图1为两级式拓扑结构主电路图，该电路由光伏电池、DC/DC升压环节、DC/AC逆变环节及电感滤波器构成。其中，Boost升压电路与其他DC/DC电路相比体积小、重量轻、效率高、结构简单和电压调节范围比较宽等特点，所以前级DC/DC环节采用Boost升压电路，同时为了避免光伏电池能量的浪费，要把Boost电路设计在连续工作模式；后级DC/AC环节采用单相全桥式逆变电路，通过对4个功率开关管进行适当控制，使逆变输出的电流与电网的电压同频同相；最后逆变输出的电流通过电感进行滤波后并入电网。

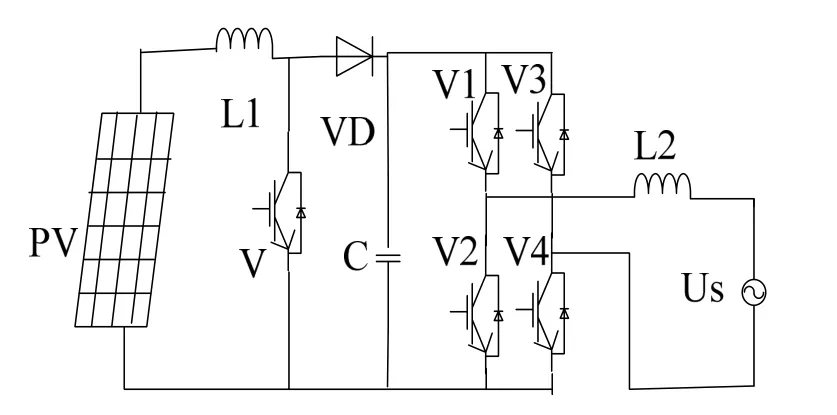
图1 主电路拓扑结构

2 光伏阵列建模

光伏电池是利用光生伏特效应将光能转变为电能的器件，光伏电池输出具有明显的非线性，易受到光照强度、环境温度的影响，工作机理相当于一个半导体发光二极管。单个光伏电池输出的功率、电压和电流都很小，实际应用通过多个光伏电池进行串并联封装在一起组成能够输出大功率的光伏组件。光伏电池模型主要分为物理模型和工程模型[7]，物理模型能够较为准确的反映光伏电池的物理特性，仿真精度高，但是，该方法复杂，需要光伏电池的内部参数；工程模型是基于物理模型基础上进行简化，利用光伏组件伏安外特性法，对开路电压、短路电流以及拟合曲线系数经行修正，使模型特性与实际光伏组件在不同光照强度和温度下特性相似，模型简单，与光伏产品提供参数对应，在研究中被广泛地使用。

2.1 工程模型

根据电子学理论知识，光伏电池典型等效电路形式为单二极管形式[8]如图2所示。

图2 光伏电池等效电路图

从图2中可以得到光伏电池的输出特性方程为：

式中：Iph为光伏电池内部光生电流，I0为光伏电池内部等效二极管的PN结反向饱和电流，q为电子电荷，K为玻尔兹曼常数，T为光伏电池所处的绝对温度，A为光伏电池内部PN结的曲线常数，Rsh为光伏电池内部的等效旁路电阻，Rs为光伏电池内部的等效串联电阻。

由急诊医师对出现严重多发伤患者实施床旁超声评估，部位包括脾肾隐窝，左肺底，右肺底，Morison陷窝，Douglas窝，双侧胸腔和子宫陷窝。CT结果以胸腹腔出现积液为阳性，超声检查以游离液体深度大于2mm为阳性[2]，医院还要对所有接受检查的患者随访3天。

公式（1）能够较好的表示了光伏电池内部基本原理，被广泛用于光伏电池的原理分析中。但是，式（1）中某些参数与外界环境因素有关，难以确定，不适合用于工程。同时，与光伏组件制造厂家提供的光伏组件的参数不同。

在式（1）基础上，文献[8]式（1）进行简化处理，推导出了光伏组件工程数学模型输出特性方程：

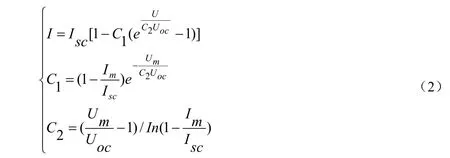
当外界环境发生变化时，通过直接对电池的4个性能参数进行修正，将不同温度及光照条件下电池参数变化曲线与环境变化趋势进行拟合。新的条件下光伏电池4个性能参数计算公式[8-10]如式（3）所示：

式中，ΔS=S/Sref-1，ΔT=T-Tref，Sref=1000W/m2、Tref=25℃为标准条件下光照强度和参考温度；a为电流温度系数，取值为0.0025/℃，c为电压温度系数，取值0.00288/℃；e为自然对数的底数；b=0.5;

根据式（2）和式（3）可以计算出任意光照强度和温度下光伏组件的输出特性。该方法不需要物理模型中复杂的参数，简便灵活，适合工程应用。

在光伏阵列中，若各个光伏组件特性相同时，由NS×NP个光伏组件构成的光伏阵列和单个光伏组件之间的关系如式（4）所示：

式中：U、I、P分别为单个光伏组件的输出电压、电流和功率，Ua、Ia、Pa分别为光伏阵列的输出电压、电流和功率。

2.2 输出特性曲线研究

本文的光伏组件使用的是由山东博泰公司生产的BTSM-180M型号，在标准测试条件下的参数如表1所示：

表1 光伏组件的参数

图3 不同温度下（S=1000w/m2）光伏电池特性曲线

图4 不同光照强度下（t=25℃）光伏电池特性曲线

3 最大功率点跟踪控制

光伏阵列输出特性易受到光照强度和温度的影响，在任意光照强度和温度下都存在一个特定的最大功率输出点。为了有效利用光伏阵列，使它发出更多的电量、输出最大的功率，因此需要最大功率点跟踪来实现光伏阵列的输出功率最大。

3.1 自适应占空比扰动法

占空比扰动法是根据电池工作在每个周期内，通过增大或减小输出占空比来改变输出功率，实现功率的寻优，扰动法步骤少，需要采样的数值少，实现起来比较简单。然而，该算法也存在着不足，扰动法只能在最大功率点附近来回扰动，存在振荡损耗。若扰动步长变小，可以减小振荡，但导致跟踪速度变慢，跟踪时间变长；若扰动步长变大，可以增大跟踪速度，使跟踪时间变短，但导致振荡变大，跟踪精度降低且损失功率增大；当外界环境发生变化时，扰动法可能会出现误判现象[14]。

为了克服占空比扰动法的缺陷，比如动态性能和稳态性能很难两者兼顾等[11]。本文提出了一种自适应占空比扰动法的算法。其控制思想与相比传统的占空比扰动法不同之处在于将扰动步长定步长变为自适应步长，本文中采用自适应步长控制算法如式（5）所示。

其中K为比例系数。

根据公式P=UI，由光伏阵列最大功率点处，dP/dI=0，可以推导出公式（6）[12]。

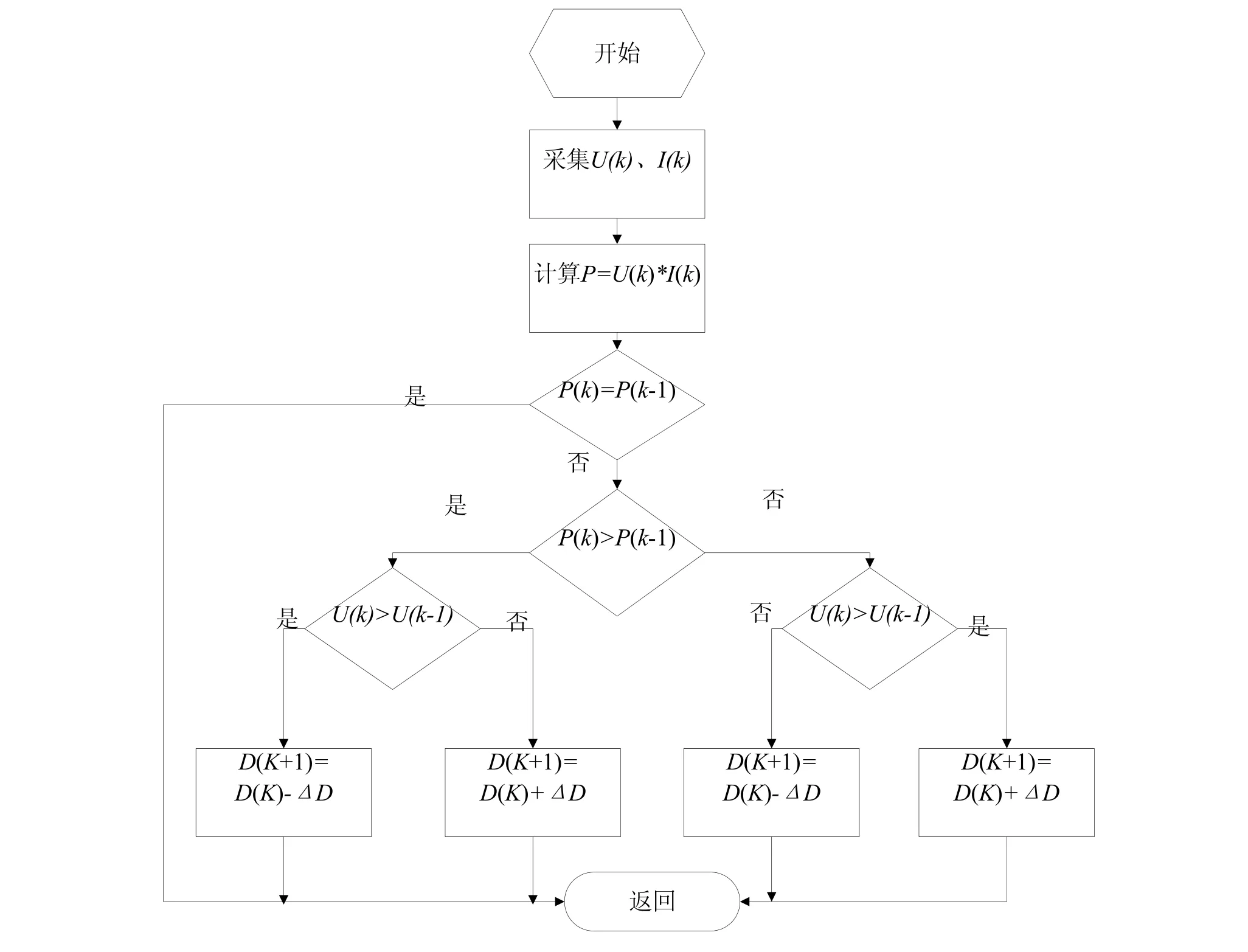
图5 占空比扰动法流程图

根据光伏阵列的P-U特性曲线，从电压为0到最大功率点电压附近左侧时，该段曲线可以近似认为是一条斜率为正的直线；从最大功率点电压附近右侧到最大电压值时，该段曲线可以近似认为是一条斜率为负的直线；在最大功率点附近时，两次采样点间曲线斜率的绝对值小于上述曲线斜率绝对值，从而实现了自适应步长，即远离最大功率点时，扰动步长较大，在最大功率点附近时，扰动步长较小，实现了在增加跟踪速度的同时增加了跟踪精度。当光伏阵列满足公式（6）时，表明此时光伏阵列已工作在最大功率点处且Boost电路中功率器件的占空比不再发生变化，从而该方法消除了光伏阵列在最大功率点的振荡现象，该MPPT算法流程图如图5所示。图中ΔD=K×|ΔP/ΔU|为DC/DC环节Boost电路中功率器件的占空比。

3.2 仿真分析

为了验证自适应占空比扰动法算法，基于Boost电路搭建其仿真模型，仿真时间为2秒，环境温度25℃，初始光照强度为500w/m2，1秒时光照强度变为1000w/m2，1.5秒时光照强度变成1500w/m2，其仿真模型输出的功率的波形图如图6所示。

从图6中可知，光照强度发生变化时，该算法仍能实现MPPT功能，在一定程度上增加了寻优的速度，同时，功率波动非常小。该算法能准确、稳定和快速实现最大功率点跟踪。

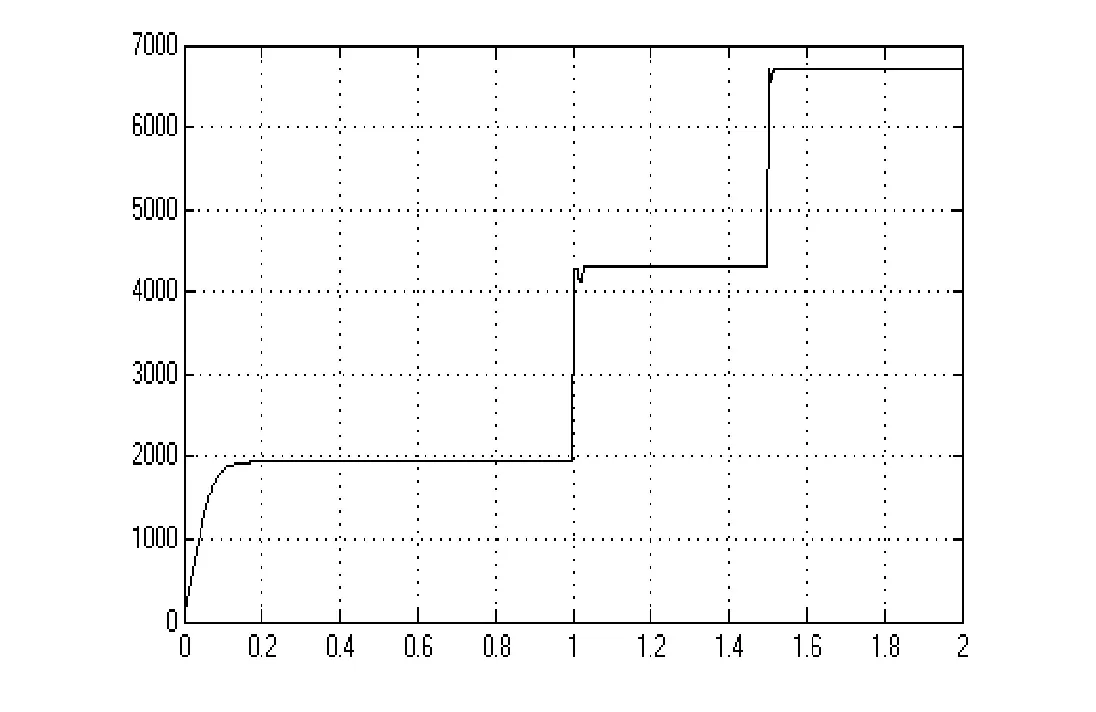
图6 自适应占空比算法的仿真结果

4 逆变控制

光伏并网系统中逆变的任务是跟踪电网电压，逆变成与电网电压同频同相的高质量正弦波的交流电流[13]。

4.1 双闭环控制

图7 双闭环控制框图

本文采用双闭环SPWM控制策略进行并网控制。外环为电压环，目的是为了控制并网逆变器直流输入端电压稳定；内环为电流环，目的是为了控制并网逆变器的输出电流与电网电压同频同相，输送到电网的功率因数近似为1[14]。首先电压环由直流侧基准电压Udref与其实际电压Udc比较，得到两者差值在PI调节器作用下输出的幅值乘以表示电网电压正弦信号后，得到了电流环的电流指令信号I*与实际电流值I0作差，经过PI调节器后得到电压信号，为了消除电网电压波动引起损耗，引入了其电压的前馈信号Uw，这两个的电压值作差后再与三角波进行调制，得到所需要的SPWM波，其控制框图如图7所示。

4.2 仿真分析

基于上述方案，搭建系统仿真模型。在标准条件下，光伏阵列输出的电压经升压后直流母线电压为350V左右，逆变后与220V/50Hz的电网电压进行并网。仿真结果如图8所示。图中为电网电压波形和逆变器输出的电流波形，从图中可知,该逆变控制方法可以快速准确的实现,逆变器输出的电流与电网电压同频同相的跟踪，从图9中可知并网电流THD含量小于5%. 达到并网的要求。

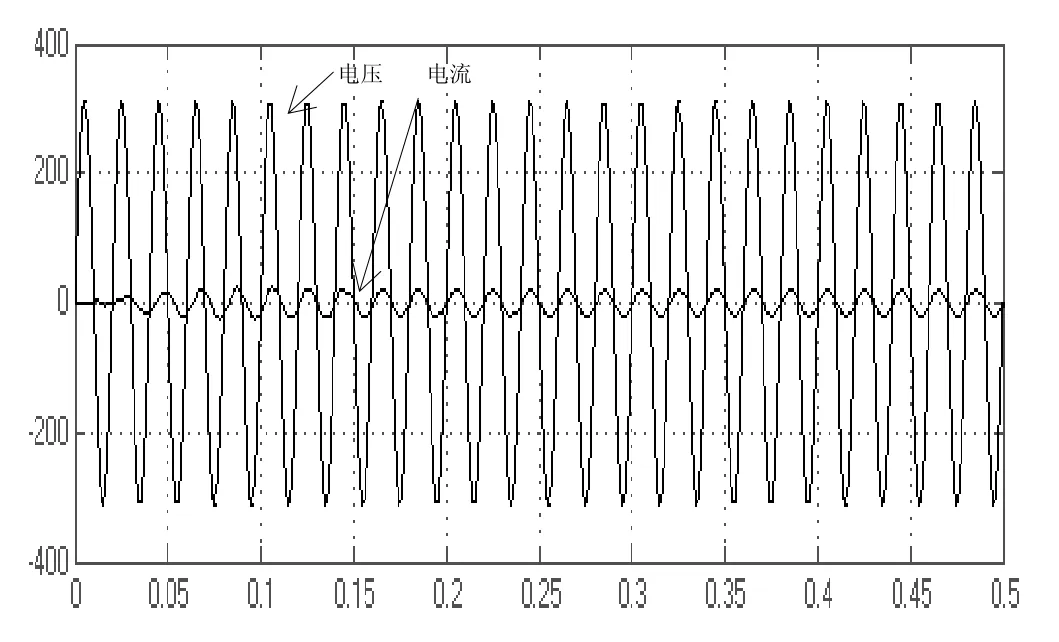
图8 并网电流与电网电压波形

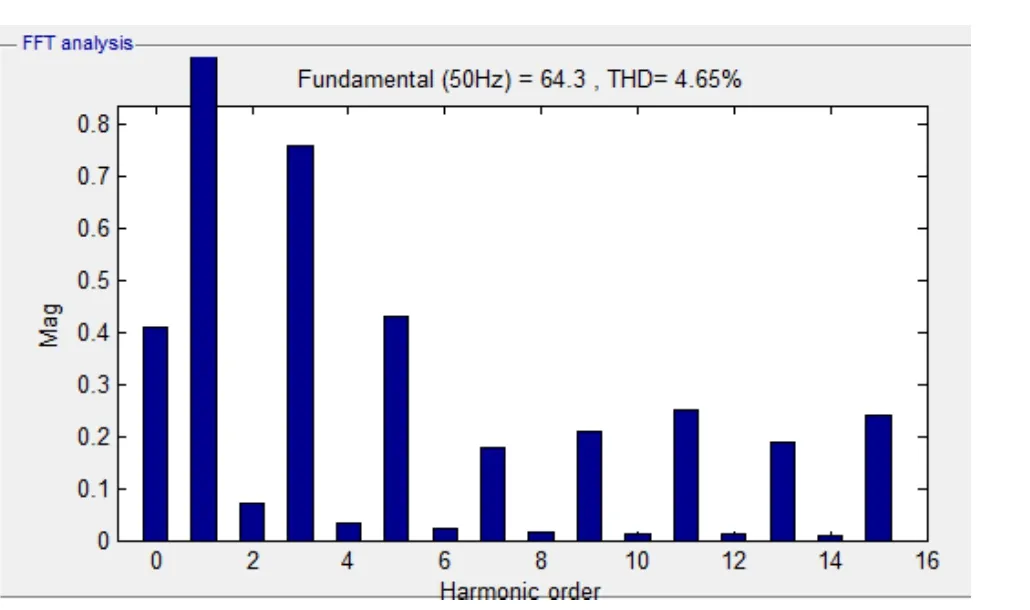
图9 并网电流FFT分析结果

5 结论

本文研究了单相两级式光伏并网系统，对系统中的光伏阵列输出特性、最大功率点跟踪技术和并网控制策略进行了仿真分析研究，得出以下结论：

（1）根据光伏电池单二极管形式数学模型进行简化推导得到了光伏组件工程模型，在此基础上，建立光伏阵列的通用仿真模型，仿真结果表明该模型能够正确反映光伏阵列在任意光照强度和温度下的输出特性，同时，也证明了光伏组件的工程数学模型能过正确的反映出光伏组件的输出特性。

（2）在对占空比扰动法的工作原理进行详细分析的基础上，根据该算法的跟踪速度和跟踪精度很难两者兼顾的不足，提出了一种自适应占空比扰动法，该算法能够弥补占空比扰动法的不足，既能提高精度又能提高速度，使光伏电池稳定、快速及准确的工作在最大功率点处。

（3）在双闭环控制中引入电网电压的前馈补偿控制，作为光伏系统的并网控制策略，通过搭建光伏并网系统的仿真模型，结果表明逆变器输出的电流与电网电压同频同相的跟踪，达到了预期的要求。

[1]Chen Hao, Gu J J. Implementation of Three-Phase Switched Reluctance Machine System for Motors and Generator.IEEE/ASME Trans. on Mechatronics, 2010, 15(3)∶421-432.

[2]杨永恒,周克亮.光伏电池建模及MPPT控制策略[J].电工技术学报,2011,26(1)∶229-234.

[3]陈丹平.光伏发电系统常用MPPT算法仿真分析综述[J].研究与设计,2012,15(7)∶9-13.

[4]郑必伟,蔡逢煌,王武.一种单级光伏并网系统MPPT算法的分析[J].电工技术学报,2011,26(7)∶90-96.

[5]杨贵恒,强生泽,张颖超,等.太阳能光伏发电系统及其应用[M].北京∶化学工业出版社,2011.

[6]吴春华,黄建明,陈卫民,等.单相光伏并网与有源滤波的统一控制[J]. 电工技术学报,2011,26(10)∶103-109.

[7]张纯杰,赵志刚,桑虎堂.光伏电池的建模综述[J].电源技术,2016,140(4)∶927-930.

[8]高金辉,邢倩,马高峰锋.光伏电池新型仿真模型及MPPT控制器的研究[J].电测与仪表,2014,51(17)∶107-111.

[9]李会平.光伏发电系统建模及并网控制策略研究[D].天津大学硕士论文,2014.

[10]WOLF P, BENDA V. Identification of PV Solar calls and modules parameters by combining statistical and analytcal methods [J]. Solar Energy. 2013. 93(7)∶ 151-157.

[11]刘邦,银段善,旭刘飞,等. 基于改进扰动观察法的光伏阵列最大功率点跟踪[J].电工技术学报,2009,24(6)∶91-94.

[12]张峥,南海鹏,金白阳. 基于MATLAB/Simulink的两级式光伏并网系统仿真分析[J].可再生能源,2010,28(1)∶81-84.

[13]Chen Xiaogao, Fu Qing, Wang Donghai. Performance analysis of PV grid-connected power conditioning system with UPS[C]. IEEE Conference on Industrial Electronics and Applications, Xi’an, 2009∶ 2172- 2176.

[14]李冬辉,王鹤雄,朱晓丹,等.光伏并网发电系统几个关键问题的研究[J].电力系统保护与控制,2010,38(21)∶208-214.

Research on the Simulation Analysis of Photovoltaic Power Grid-connected System Based on Improved P&Q Algorithm

ZHENG Jun-guan WANG Suo-he
(Shijiazhuang Tiedao University Shijiazhuang Hebei 050043 China)

The output characteristics of PV calls are no-linear. A practical model for photovoltaic cell was designed by using MATLAB/Simulink based on the engineered model of photovoltaic cell model. PV systems-perturb and observe algorithm（P&Q）is investigated. A modified P&Q algorithm is proposed for the improvement of P&Q algorithm. The control of photovoltaic grid-connected system is founded by the technology of double closed-loop control. Finally a photovoltaic generation system is constructed with simulation software. Simulation results demonstrate the validity of the model of PV array can be simulated in any condition the output characteristics of PV calls .The improvement of P&Q algorithm make the photovoltaic system quickly and track the maximum power point accurately .Besides，the output current of PV system and the voltage of public power grid with same frequency and phase through the double closed-loop control.

photovoltaic grid-connected system pv array the improvement of MPPT algorithm double closed-loop control

A

1673-1816(2017)03-0072-08

2016-06-18

郑俊观（1992-），男，硕士研究生，研究方向新能源发电与控制技术方面的研究。