基于改进刚体弹簧方法的断续双裂隙砂岩强度及裂纹扩展特征研究

， ，，

(1.南昌大学 建筑工程学院，南昌 330031；2.湖州职业技术学院 建筑工程学院，浙江 湖州 313000)

基于改进刚体弹簧方法的断续双裂隙砂岩强度及裂纹扩展特征研究

牛江瑞1,2，姚池1，杨建华1，周创兵1

(1.南昌大学 建筑工程学院，南昌 330031；2.湖州职业技术学院 建筑工程学院，浙江 湖州 313000)

为研究含非共面双裂隙砂岩的强度及裂纹扩展特征，以室内试验结果标定砂岩细观参数，建立含不同岩桥倾角的双裂隙数值计算模型，采用改进刚体弹簧方法对其单轴压缩过程进行模拟。基于模拟结果，研究了岩桥倾角对起裂应力、峰值强度、破坏模式和裂纹扩展特征的影响。结果表明：岩桥倾角<60°，起裂应力和峰值强度均随岩桥倾角增大而减小，岩桥倾角>60°，均随岩桥倾角增大而增大；根据岩桥倾角不同，裂隙试样破坏模式呈现单一翼裂纹轴向贯通破坏、翼裂纹与翼裂纹搭接贯通破坏和翼裂纹与预制裂纹搭接贯通破坏3种类型；岩桥倾角对岩桥破坏程度有影响，60°岩桥贯通最易，0°和120°岩桥贯通最难。研究结果可为岩土工程的稳定分析提供参考。

断续双裂隙砂岩； 裂隙扩展；各向异性；岩桥倾角；裂纹贯通；刚体弹簧方法

1 研究背景

自然界岩石中广泛存在着不同分布形式和规模的裂隙、弱面、孔洞和断层等初始缺陷，导致岩石材料在外部荷载作用下展现出不连续性、非均质性、各向异性和非线性等复杂的力学性质[1-2]。研究表明，岩石工程的失稳破坏主要是由于其内部初始缺陷的起裂、扩展和贯通过程所控制。因此，深入开展裂隙岩石强度特性和破坏过程中微裂纹扩展贯通规律的研究，对于确保岩土工程的稳定具有重要的实践意义。

国内外学者对裂隙岩体力学行为进行了大量卓有成效的研究。Park等[3]对含张开和闭合预制裂隙的类岩石材料分别进行单轴压缩试验，观察到了翼裂纹、共面和倾斜次生裂纹3种裂纹类型，并发现闭合裂隙试样和张开裂隙试样的主要区别是，其起裂应力大于张开裂隙试样的起裂应力；Yang等[4-5]通过在真实岩石试样上预制单裂隙和双裂隙，分析了裂隙几何分布对岩石强度变形、声发射分布规律和裂纹扩机制的影响，并总结了9种裂纹扩展类型；康石磊等[6]采用颗粒流程序(PFC)对含有2种倾角组合的类岩石裂隙试样压缩过程中裂隙增长与轴向应力和接触应力的关系进行了分析，得出了裂隙增长与应力增长有一定关系，但不成比例的结论；陈新等[7-8]通过对一组多裂隙试件的室内压缩试验，探讨了节理倾角、间距和连通率等对岩体强度和变形的影响。室内试验对裂隙岩体的研究局限于试样的宏观力学行为，而数值模型相对室内试验更为经济，对于进一步揭示岩石的细观破坏机理，提高对岩石破坏过程的认识水平具有重要意义。Zhang等[9-10]通过分析单、双裂隙数值试件裂纹扩展过程中细观位移场和力场的演化规律，揭示了裂纹扩展贯通的力学机理；唐谦等[11]模拟并分析了不同围压下含张开单裂隙岩体的裂纹扩展过程，利用位移场从细观角度对裂纹的扩展机制进行了探讨；姚池等[12]采用改进刚体弹簧方法，模拟得到不同围压下不同倾角数值试件的破坏模式和抗压强度，定性和定量地描述了由于软硬互层结构引起的抗压强度各向异性。

近年来，数值模拟在岩石材料力学性质研究方面取得了显著进展，但是已有研究成果大都基于离散元法来模拟岩石材料的损伤过程。虽然离散单元法是一种相对适合于解决非连续问题的数值方法，但是其所需细观参数无法直接通过试验获得，且不少方法具有明显的网格依赖性。鉴于此，本文采用姚池等[12-14]提出的以随机均布Voronoi图[15]为基本网格形式，很大程度上消除了一般离散单元法所具有的网格依赖性(主要指强度和弹性模量对网格的依赖性)的改进刚体弹簧方法来对预制张开双裂隙岩石的单轴压缩室内试验进行模拟，研究了岩桥倾角对裂隙岩石试样强度参数及裂纹扩展特征的影响。

2 改进刚体弹簧方法基本原理

改进刚体弹簧方法是一种可以显示模拟微裂隙开裂、扩展和贯通渐进破坏过程的细观数值方法。其将岩石材料看作由多边形刚性颗粒胶结而成的复合材料，相邻块体界面应力通过界面上均布的法向和切向的弹簧控制，当界面应力超过抗拉强度和抗剪强度时，胶结界面会发生拉裂破坏或剪切滑移破坏。相比于最初提出的刚体弹簧方法，改进刚体弹簧方法采用均布弹簧代替形心处的弹簧，可以有效描述界面的渐进破坏。界面的弹性性质由法向刚度(kn)和切向刚度(ks)2个参数表征，应力与界面相对位移相关。在二维条件下有

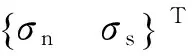
(1)

其中

(2)

式中：σn和σs分别为法向应力和切向应力；{Δu}为界面两侧的相对位移向量。利用虚功原理，并对域中所有界面和边界进行积分，可以得到总体的线性平衡方程，即

[K]{U}={Q}。

(3)

式中：[K]为总体刚度矩阵；{U}为总体位移向量；{Q}为总体荷载向量。总体刚度矩阵和总体荷载向量的获得过程与有限元类似，为所有块体平衡方程的集合。矩阵和向量的具体形式参见文献[13-14]。与常规离散单元方法不同，改进刚体弹簧方法的界面刚度参数与材料的宏观弹性参数可以建立显式的关系，对于各向同性材料，前期研究得到了如下关系：

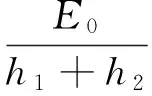
(4)

r=ks/kn=4.025v4-6.087v3+

6.022v2-3.966v+1 ；

(5)

E/E0=-0.629 1r4+1.617r3-1.678r2+

1.174r+0.516 2。

(6)

式中：E和v分别为材料的宏观弹性模量和泊松比；h1和h2分别为界面到相邻两块体形心的距离；E0和r为中间变量。因此，宏观弹性模量和泊松比可以直接作为输入参数，然后通过式(4)、式(5)、式(6)计算界面细观刚度参数。

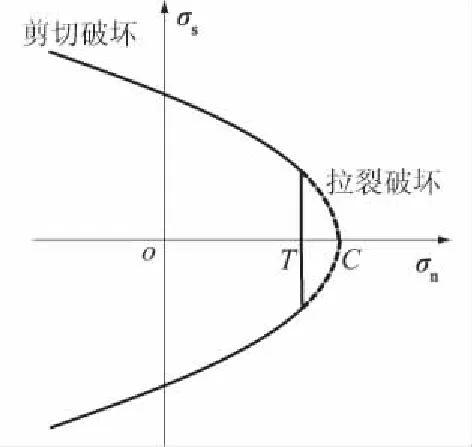
图1 界面破坏准则Fig.1 Failure criterion of interface

3 破坏准则

在刚体弹簧方法中，材料的宏观力学行为完全受界面的控制。同样地，宏观开裂过程也直接依赖于界面的细观强度,因此，需要采用合适的细观界面破坏准则。这里，考虑2种独立而互补的破坏模式，即拉裂破坏和剪切滑移破坏。当界面法向正应力σn超过界面抗拉强度T时，发生拉裂破坏;当界面切向应力超过界面抗剪强度时，发生剪切破坏。对于岩石材料，剪切强度与法向应力相关，且通常具有非线性关系。因此，采用二次非线性的抗剪强度准则来定义界面的抗剪强度。本文采用的破坏准则可以表述为

(7)

式中：Fs为剪切应力；Ft为张拉应力;B和C为破坏参数。屈服面在应力空间中的形态如图1所示。

4 数值模型构建及细观参数标定

4.1 数值模型构建

本文采用改进刚体弹簧法对文献[5]中预制双裂隙砂岩单轴压缩试验进行了模拟，分析了不同岩桥倾角β(0°，30°，60°，90°，120°)对其强度及裂纹扩展特征的影响。该砂岩尺寸为80 mm×160 mm×30 mm的棱柱体，预制裂隙长2a=15 mm，宽d=2 mm，裂隙倾角α=30°，岩桥长2b=18 mm，倾角为β，如图2(a)所示。根据Voronoi网格均匀随机生成算法，构建相同尺寸的数值岩样模型如图2(b)所示，共包含8 537个大小相近的多边形块体颗粒，颗粒接触面通过均布的法向和切向弹簧传递力的作用，如图2(c)所示。模拟采用位移控制的加载方式，试件下端固定，上端施加位移荷载，分1 000步加载，每步位移5×10-6m。基本力学参数见表1。

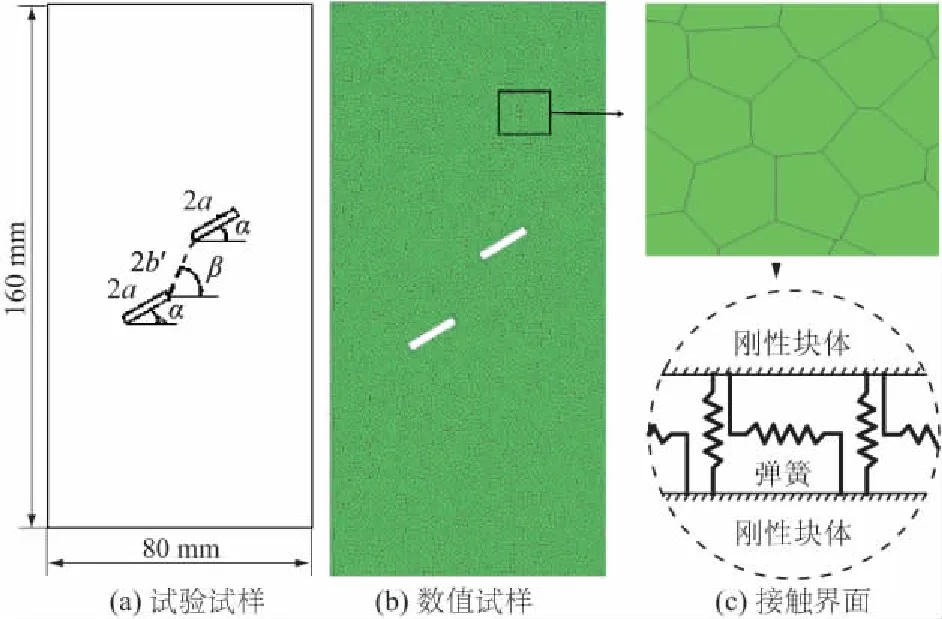
图2 含张开单裂隙砂岩试样示意图Fig.2 Sketch of sandstone sample containing a single open fissure

4.2 细观参数标定

为了得到与真实岩石性质接近的力学特性，校准通过试错法进行，通过反复调整模型强度参数(B，C，T)，最终得到一组细观参数，如表2所示。

表1 完整砂岩试样宏观力学参数Table 1 Macro-mechanical parameters of intact sandstone

表2 数值模拟所用细观参数Table 2 Input micro-parameters for simulation

模拟得到的完整岩石单轴压缩应力-应变曲线和破坏模式与试验结果基本吻合，如图3所示。

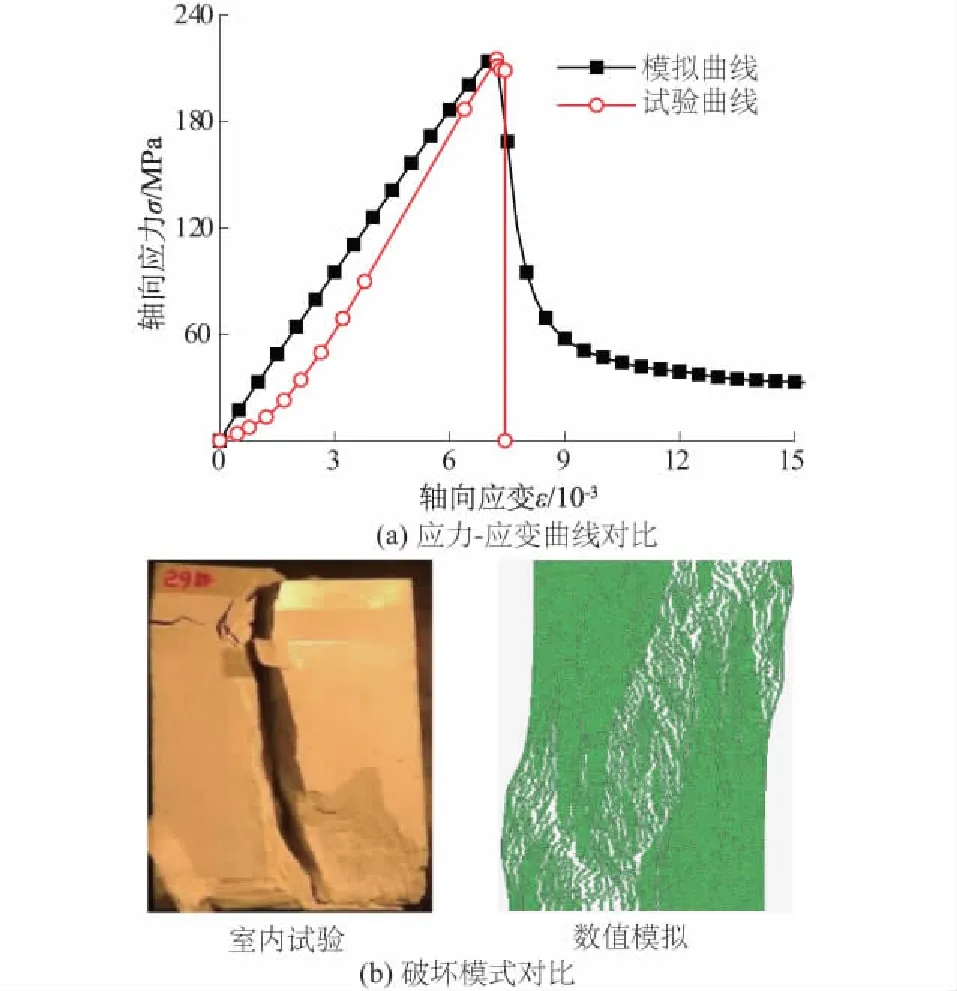
图3 完整砂岩试样试验和模拟结果对比Fig.3 Comparison between laboratory test and numerical simulation on intact rock under uniaxial compression

由图3(a)可知，数值模拟和室内试验得到的单轴抗压强度分别为213.86 MPa和215.98 MPa，相差0.9%；峰值应变分别为7×10-3和7.24×10-3，相差3.31%，相差较大，造成此差距的原因可通过应力-应变曲线对比来解释。图3(a)中试验曲线从加载开始没有直接进入线性阶段，而先出现真实岩样初始缺陷闭合的下凹段；模拟试样内部微粒均匀分布，且没有考虑初始裂隙存在，不能体现初始的非线性压密阶段，从而使得轴向应变较试验值小。但总体上模型模拟得到的完整砂岩试样的单轴压缩应力-应变曲线和室内试验结果吻合良好。由图3(b)可以看出，数值模拟和室内试验的最终破坏模式也比较接近，均为轴向张拉破坏。通过以上分析可见，本程序基本可以完整再现砂岩试样破裂过程和破裂模式。

5 模拟结果分析

5.1 岩桥倾角对岩体强度及宏观破坏模式的影响

采用表2中的细观参数，对Yang等[5]室内试验进行模拟，得到起裂应力和峰值强度随岩桥倾角增大的变化趋势，呈 U型分布，见图4。由图4可知，模拟得到的峰值强度随岩桥倾角增大表现出先减小后增大的趋势，此趋势与室内试验结果一致。当岩桥倾角为60°时，峰值强度最低，这是由于其发生预制裂隙内侧岩桥贯通破坏所致。从图4还可以得出起裂应力随岩桥倾角增大表现出与峰值强度相同的变化趋势，起裂应力与峰值强度比值变化范围为0.4～0.5，该比值与当前国际上0.3～0.5的研究结果较为一致。

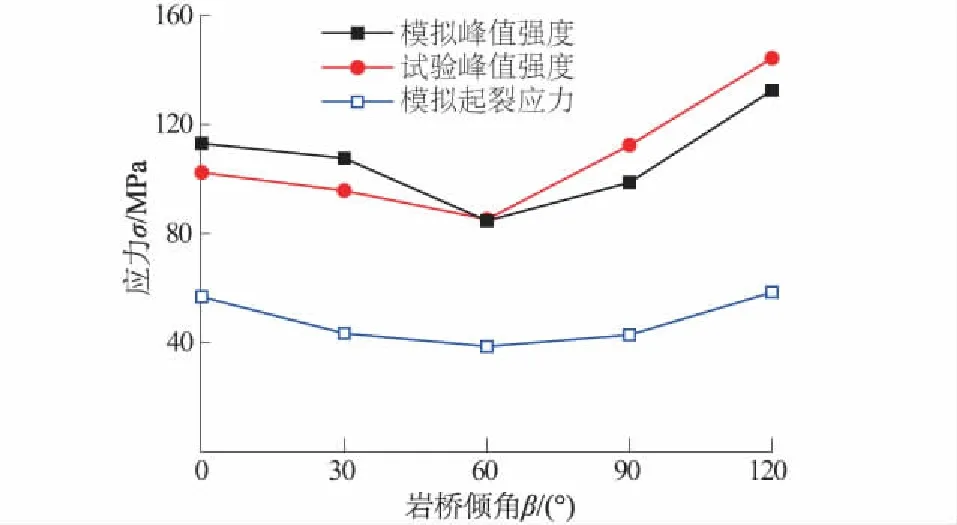
图4 峰值强度及裂纹起裂应力与岩桥倾角之间的关系Fig.4 Relationships between peak stress,crack initiation stress and rock bridge inclination

图5展示了模拟得到的破坏模式与室内试验结果的对比，由该图可知，当岩桥倾角较小时(β=0°和β=30°)，裂隙试样岩桥破坏不明显，翼裂纹自预制裂隙两端起裂，沿最大主应力方向扩展贯通，发生单一翼裂纹轴向贯通破坏；当岩桥倾角β=60°时，预制裂隙外端翼裂纹起裂并沿最大主应力方向扩展，直至贯通，而预制裂隙内端翼裂纹起裂并搭接，导致岩桥贯通破坏，至此试样发生翼裂纹搭接贯通破坏；当岩桥倾角较大(β=90°和120°)时，预制裂隙内部由翼裂纹与预制裂隙搭接，形成“鱼眼”状的破坏区域，预制裂隙外部翼裂纹沿最大主应力方向扩展贯通，发生翼型裂纹与预制裂纹搭接贯通破坏。这些破坏模式均与室内结果表现出良好的一致性。

图5 不同倾角试样最终破坏模式对比Fig.5 Comparison of failure mode between test and numerical simulation for specimens with different rock bridge inclinations

由上述结果可知，模型能够很好地再现裂隙岩样的强度和破坏模式等宏观力学特性，将本模型用于模拟含张开单裂隙试样的破坏过程是完全可行的。下面就岩桥倾角对裂隙岩石微裂纹扩展特征进行一些分析和讨论。

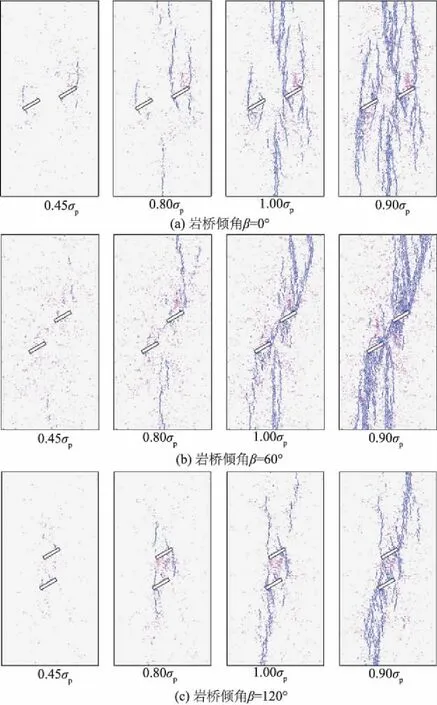
图6 不同岩桥倾角裂纹扩展过程Fig.6 Crack propagations in specimens with different rock bridge inclinations

5.2 微裂纹扩展过程分析

基于不同岩桥倾角的数值裂隙试样，图6分别给出了其对应轴向应力σ=0.45σp，σ=0.80σp，σ=σp和峰后σ=0.9σp时的裂纹扩展图(σp为轴向应力峰值强度)，其中蓝色表示张拉裂隙，红色表示剪切裂隙，长度和粗细表示大小。由图(6)可知：

(1) 当岩桥倾角β=0°时，在加载过程中，首先在预制裂隙外端开裂，然后在预制裂隙内端以及试样上下端部开裂，形成翼裂纹和远场裂纹，这主要是由于预制裂隙端部和试样上下端部容易形成应力集中区所致。在翼裂纹和远场裂纹形成后，均沿最大主应力方向扩展，并最终导致试样失稳破坏。在整个加载过程中，岩桥始终保持完整，这主要是由于岩桥倾角较小，有效剪力虽然不能够驱动与裂隙走向近乎平行的剪切裂纹，但是仍能使预制裂隙端部张拉裂纹起裂和扩展。岩桥倾角β=30°时的破坏过程和0°试样的破坏过程相似,这里就不再赘述。

(2) 当岩桥倾角β=60°时，峰值应力以前，裂纹首先在试样上、下端部萌生，并沿最大主应力方向扩展，最终与翼裂纹搭接。当轴向应力达到峰值强度时，岩桥由2条预制裂隙内侧萌生的翼裂纹交汇贯通，裂纹中既有张拉裂纹又有剪切裂纹，但以张拉裂纹为主。如果继续加载，最终会形成翼裂纹与翼裂纹搭接贯通破坏。由于岩桥倾角为60°的试样，其岩桥易在拉剪复合应力作用下贯通破坏，导致其峰值强度较低。

(3) 当岩桥倾角β=120°时，一方面翼裂纹从预制外端萌生，沿最大主应力方向扩展，并与另一条预制裂隙内端搭接，形成“鱼眼”状的破坏区域；另一方面，翼裂纹又沿最大主应力方向向试样端部扩展。但是这种破坏模式下，岩桥并没有完全贯通。因此岩桥倾角为120°的试样的峰值强度也较大。岩桥倾角为90°时的试样与其具有类似的破坏过程，这里就不再赘述。

6 结 论

采用改进刚体弹簧方法，对预制双裂隙砂岩单轴压缩试验进行了模拟，研究了岩桥倾角对裂隙试样强度特征、破坏模式和破坏过程的影响。基于模拟结果，得出以下结论。

(1) 改进刚体弹簧方法可以从定性和定量2个角度再现双裂隙砂岩试样破坏过程中的强度特征和破坏模式，模拟结果与室内试验观察到的结果表现出良好的一致性。

(2) 与完整砂岩试样相比，裂隙砂岩试样峰值强度明显降低，且降低幅度与岩桥倾角有关。峰值强度和起裂应力均随岩桥倾角增大表现出先减小后增大的趋势，呈 U型分布。当岩桥倾角为60°时，峰值强度和起裂应力最低。

(3) 根据不同岩桥倾角将裂隙试样破坏模式分为单一翼裂纹轴向贯通破坏、翼裂纹与翼裂纹搭接贯通破坏、翼裂纹与预制裂纹搭接贯通破坏3种类型。

(4) 根据裂隙裂纹扩展特征可以看出，0°和30°倾角试样岩桥基本没有破坏；90°和120°试样岩桥形成“鱼眼”状的破坏区域，并未完全贯通；而60°试样岩桥倾角直接贯通。因此60°倾角岩桥试样与其他倾角岩桥试样相比，其峰值强度最低。同时还可以看出不同岩桥倾角试样的3种破坏模式从本质上都是由张拉应力引起的张拉裂纹交汇贯通的结果。

[1] 夏才初,孙宗颀.工程岩体节理力学[M].上海: 同济大学出版社,2002: 100-101.

[2] HUDSON J A,HARRISON J P.Engineering Rock Mechanics: An Introduction to the Principles[M].U.S.A.: Elsevier,2000.

[3] PARK C H,BOBET A.Crack Coalescence in Specimens with Open and Closed Flaws: A Comparison[J].International Journal of Rock Mechanics and Mining Sciences,2009,46(5): 819-829.

[4] YANG S Q,JING H W.Strength Failure and Crack Coalescence Behavior of Brittle Sandstone Samples Containing a Single Fissure under Uniaxial Compression[J].International Journal of Fracture,2011,168(2): 227-250.

[5] YANG S Q,TIAN W L,HUANG Y H,etal.An Experimental and Numerical Study on Cracking Behavior of Brittle Sandstone Containing Two Non-coplanar Fissures Under Uniaxial Compression[J].Rock Mechanics and Rock Engineering,49(4):1497-1515,doi:10.1007/s00603-015-0838-3.

[6] 康石磊,阳军生,杨 峰.含裂隙类岩试样破坏行为的宏细观数值分析[J].长江科学院院报,2016,33(4): 71-77.

[7] 陈 新,廖志红,李德建.节理倾角及连通率对岩体强度、变形影响的单轴压缩试验研究[J].岩石力学与工程学报,2011,30(4): 781-789.

[8] 陈 新,李东威,王莉贤,等.单轴压缩下节理间距和倾角对岩体模拟试件强度和变形的影响研究[J].岩土工程学报,2014,36(12): 2236-2245.

[9] ZHANG X P,WONG L N Y.Cracking Processes in Rock-like Material Containing a Single Flaw under Uniaxial Compression: A Numerical Study Based on Parallel Bonded-particle Model Approach[J].Rock Mechanics and Rock Engineering,2012,45(5): 711-737.

[10] ZHANG X P,WONG L N Y.Loading Rate Effects on Cracking Behavior of Flaw-contained Specimens under Uniaxial Compression[J].International Journal of Fracture,2013,180(1): 93-110.

[11] 唐 谦,李云安.围压对岩石裂纹扩展影响的颗粒流模拟研究[J].长江科学院院报,2015,32(4): 81-85.

[12] 姚 池,李 瑶,姜清辉,等.应力作用下软硬互层岩石破裂过程的细观模拟[J].岩石力学与工程学报,2015,34(8): 1542-1551.

[13] 姚 池，姜清辉，邵建富，等.一种模拟岩石破裂的细观数值计算模型[J].岩石力学与工程学报，2013，32(增2)：3146-3153.

[14] YAO C,JIANG Q H,SHAO J F.Numerical Simulation of Damage and Failure in Brittle Rocks Using a Modified Rigid Block Spring Method[J].Computers and Geotechnics,2015,64: 48-60,doi: 10.1016/j.compgeo.2014.10.012.

[15] FORTUNE S.A Sweepline Algorithm for Voronoi Diagrams[J].Algorithmica,1987,2(1/4): 153-174.

(编辑：姜小兰)

Numerical Study on Strength and Crack Coalescence Behavior ofSandstone Containing Two Pre-existing Non-coplanar FissuresBased on Improved Rigid Body Spring Method

NIU Jiang-rui1,2,YAO Chi1,YANG Jian-hua1,ZHOU Chuang-bing1

(1.School of Civil Engineering and Architecture,Nanchang University,Nanchang 330031,China; 2.Institute of Civil Engineering,Huzhou Vocational and Technical College,Huzhou 313000,China)

In order to study the strength and crack coalescence behavior of sandstone containing two pre-exisiting non-coplanar fissures,a modified Rigid Body Spring Method is proposed to simulate the process of uniaxial compression tests,and a set of micro-parameters calibrated by uniaxial compression laboratory test results was used toset up a model of fissured rock samples containing two pre-exisiting non-coplanar fissures.On the basis of the simulated results,the influence of rock bridge inclination on crack initiation stress,peak strength,failure mode and crack coalescence behavior was investigated.Results show that crack initiation stress and peak strength both decreased in the presence of a rock bridge inclination smaller than 60°,and vice versa.According to the differences of the rock bridge inclination,the failure mode of specimens could be divided into three types: the penetration failure of single wing crack,the penetration failure of the coalescence of wing crack and the penetration failure of the coalescence between wing crack and prefabricated fissures.Rock bridge inclination has some impact on the failure degree of the rock bridge,and it is easy to coalesce for 60° rock bridge but hard for 0° and 120° rock bridge.

two pre-exisiting non-coplanar fissures in sandstone; crack propagation; anisotropy; rock bridge inclination; crack penetration; rigid body spring method

TU45

A

1001-5485(2017)10-0102-05

2016-06-12;

2016-06-29

国家自然科学基金项目(51409138,51509126,51509104)；江西省自然科学基金项目(20161BAB216116)

牛江瑞(1990-)，男，河南安阳人，硕士研究生，主要从事岩土工程理论和数值方面计算的研究，(电话)15067247556(电子信箱)jrniuncu@163.com。

姚 池(1986-)，男，湖北汉中人，副教授，博士，主要从事岩石细观破坏及水力耦合数值模型方面的研究，(电话)18679193769(电子信箱)chi.yao@ncu.edu.cn。

10.11988/ckyyb.20160591 2017,34(10):102-106,113