钢材拉伸试验数据的同质性判别

刘 岑 杨 帆 吴元祥 刘 兵 张 磊 张红卫

(1.湖北轻工职业技术学院 湖北 武汉:430070；2.武汉软件工程职业学院 湖北 武汉:430205)

钢材拉伸试验数据的同质性判别

刘 岑1杨 帆2吴元祥2刘 兵2张 磊2张红卫2

(1.湖北轻工职业技术学院 湖北 武汉:430070；2.武汉软件工程职业学院 湖北 武汉:430205)

具有同质性的拉伸试验数据是确定钢材机械性能指标的依据，判别试验数据的同质性，剔除无效数据，是分析拉伸试验数据具有同质性的前提。应用数理统计理论，建立了试验数据同质性的判别方法。基于桥梁用Q420NHY中厚板拉伸试验数据，在双侧置信度为99%时，判别了试验数据的同质性，确定了Q420NHY钢的机械性能指标。研究表明：拉伸试验数据的同质性对钢材机械性能指标的影响不可忽视。

拉伸试验数据；机械性能；同质性；数理统计；判别；Q420NHY钢

抗拉强度与下屈服强度是钢材的强度指标，断后伸长率是钢材的塑性指标，它们是钢材机械性能指标的重要组成部分，也是确定机械零件材料与进行其强度设计的基础与依据。目前，工程上是通过拉伸试验确定钢材的抗拉强度、下屈服强度与断后伸长率。

钢材的机械性能不但与其化学成分、冶炼方法、结构形式、热处理方法有关，而且涉及到拉伸试验环境条件，因此，我国采用有关标准[1-3]规范钢材的化学成分、冶炼方法、结构形式、热处理方法等因素，使相同牌号的钢材具有基本相同的机械性能，即按相同标准获得的钢材具有同质性；同时还采用有关标准[4]规范钢材的拉伸试验，以获得具有同质性的试验数据，能真实反映钢材机械性能强度与塑性等方面的指标。

从数理统计理论角度可认为，具有同质性的钢材是无限的总体，工程上只能对有限的样本进行试验，获得钢材的试验数据，从而分析与确定同质性钢材的机械性能指标。由于影响钢材同质性的生产与试验因素比较多，试验数据分散性比较大[5-7]，必须对试验数据的同质性进行判别，剔除因意外因素影响而形成的非同质性无效数据；因此，如何判别试验数据的同质性，剔除无效数据，是确定钢材机械性能指标的基础。文中应用数理统计理论和利用概率论的t分布[8,9]，建立了判别试验数据同质性的方法，基于桥梁用钢Q420NHY中厚板的拉伸试验数据，在在双侧置信度为99%时，确定了其抗拉强度、下屈服强度与断后伸长率的平均值与精密度。

1 基本方法

如果根据参考文献[4]通过拉伸试验测量钢材机械性能某一指标X的p组试验数据Xi(i=1，2，…，n)，不难得到n组试验数据的平均值与精密度：

(1)

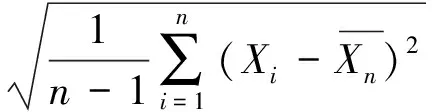
(2)

概率论的t分布是判别试验数据同质性的有效方法[10-16]，如图1所示，在双侧置信度为(1-α)时，由试验数据组数n和t分布性质，可确定t分布系数tn-1,0.5α，作为试验数据同质性的判别依据，文中所用的t分布系数见表1[9]。

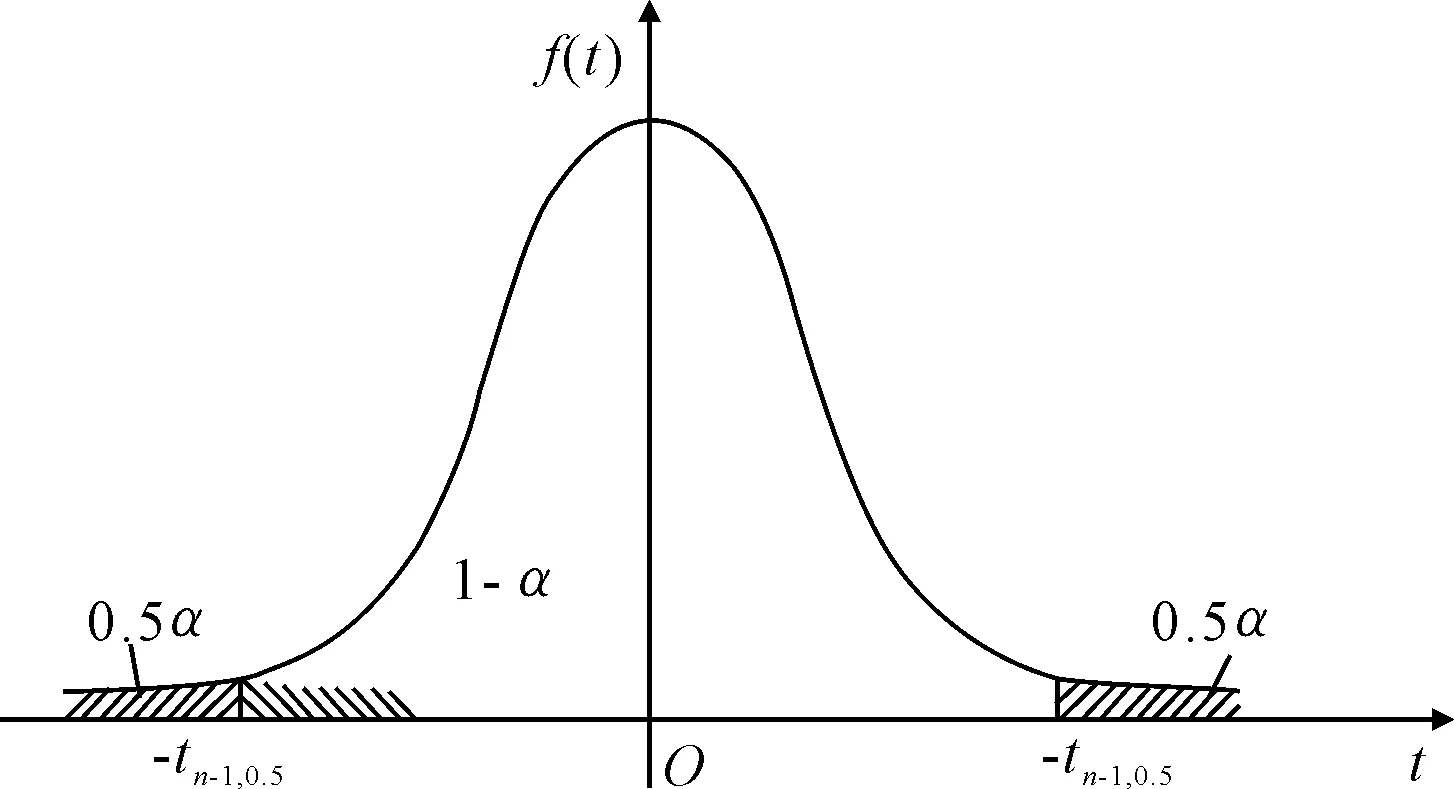
图1 t分布的双侧置信度区间

表1 系数t

在双侧置信度为(1-α)时，第i个试验数据Xi与其他(n-1)个试验数据是否具有同质性的判据为：

(3)

如果

|ti|>tn-1,0.5α

(4)

则有(1-α)的把握认为，Xi与其他(n-1)个试验数据的平均值不具有同质性，不是有效试验数据，需要剔除；剔除无效数据，应从试验数据的最大值或者最小值开始，每剔除1个无效数据，都要计算其余数据的平均值与精密度，再进行同质性判别；在剔除非同质性的无效数据以后，对余下的有效数据需要重新计算平均值与精密度，作为确定机械性能指标均值与标准差的基础，或者作为计算测量不确定度的依据。

从图1可知，α是将同质性的有效数据作为无效数据剔除的风险概率，由于工程上认为小概率事件在一次试验中是不可能发生的，因此通常取α=0.05，0.02或者0.01，本文取α=0.01，即在双侧置信度为99%时，判别试验数据同质性或有效性，同时相应的风险概率只有1%。

2 实例

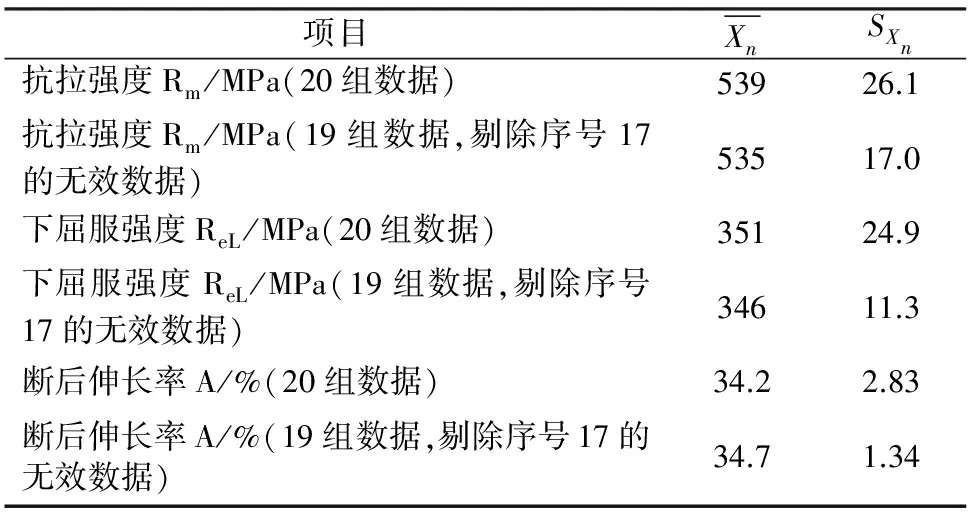
Q420NHY(中厚板)是常用的桥梁用钢，文献[6]获得了其抗拉强度、下屈服强度与断后伸长率的20组试验数据，见表2。

(1)抗拉强度同质性判别。抗拉强度最大值为第17组试验数据Rm17=625MPa，用式(3)与式(4)，可知判据|ti|=3.295>t19,0.005=2.861，因此，该数据不具有同质性是无效的。对余下的19组试验数据重新统计，得到的统计数据列入表3；再一次用式(3)与式(4)可知，余下19组抗拉强度试验数据的判据|ti|

表2 Q420NHY钢的20组试验数据

将表2的试验数据代入式(1)与式(2)，可分别得到20组试验数据的平均值与精密度，见表3。

表3 试验数据统计

(2)下屈服强度同质性判别。下屈服强度最大值为第17组试验数据ReL17=446MPa，用式(3)与式(4)，可知判据|ti|=3.815>t19,0.005=2.861，因此，该数据不具有同质性是无效的。余下的19组试验数据重新统计，得到的统计数据列入表3；再一次用式(3)与式(4)可知，余下19组下屈服强度试验数据的判据|ti|

(3)断后伸长率同质性判别。断后伸长率最小值为第17组试验数据A17=23.5%，用式(3)与式(4)，可知判据|ti|=3.781>t19,0.005=2.861，因此该数据不具有同质性是无效的。将余下的19组试验数据重新统计，得到的统计数据列入表3；再一次用式(3)与式(4)可知，余下19组断后伸长率试验数据的判据|ti|

(4)讨论。1)由表3可知：不具有同质性的无效试验数据，对钢材机械性能指标有比较大的影响，因此，在确定钢材机械性能指标时，必须判别试验数据的同质性，剔除非同质性的无效试验数据；2)有关文献[5,6]在没有判别试验数据的同质性时，利用所有试验数据确定钢材机械性能指标[5,6]或者计算测量的不确定度[7]，是值得商榷的；3)从文中分析可以发现，表2中第17号试验数据的三个指标(抗拉强度、下屈服强度与断后伸长率)分别不具备同质性，因此对于这种用同一试样得到的试验数据，必须分析非同质性产生的原因，以利于改进生产与试验，获得质量稳定的钢材与具有同质性的试验数据。

3 结论

(1)拉伸试验数据的同质性对钢材机械性能指标有较大的影响，如果不剔除非同质性的无效数据，可能得到不正确的结论；文中基于数理统计理论和利用概率论的t分布，在所要求的双侧置信度时，文中建立了试验数据同质性的判别方法。

(2)在双侧置信度为99%时，判别了桥梁用钢(中厚板)Q420NHY拉伸试验数据的同质性，在剔除非同质性的无效试验数据的前提下，认为其抗拉强度的平均值与精密度分别为535MPa与17.0MPa、下屈服强度的平均值与精密度分别为346MPa与11.3MPa，断后伸长率的平均值与精密度分别为34.7%与1.34%。

(3)对于非同质性试验数据，必须分析其产生的原因，以利于改进生产，获得质量稳定的钢材。

[1] GB/T 699-2015.优质碳素结构钢[S].

[2] GB/T 713-2014.锅炉和压力容器用钢板[S].

[3] GB/T 3077-2015.合金结构钢[S].

[4] GB/T 228-2010.金属材料 拉伸试验[S].

[5] 黄泽,缪存坚,李涛,等.预拉伸奥氏体不锈钢常温拉伸力学性能试验研究[J].压力容器,2013,30(6):7-11.

[6] 郑津洋,王珂,黄泽,等.液氮温度下奥氏体不锈钢强度试验研究[J].压力容器,2014,31(8):1-6.

[7] 薛欢.桥梁用钢拉伸试验不确定度的评定[J].武汉工程职业技术学院学报，2017,29(1):11-14.

[8] 徐灏.机械强度的可靠性设计[M].北京:机械工业出版社,1984.

[9] 化学工程手册编辑委员会.化工应用数学[M].北京:化学工业出版社,1983:23-28,369-375.

[10] 刘岑,吴元祥,刘兵,等.奥氏体不锈钢S30408抗拉强度分布规律研究[J].河北工业科技,2016,33(1):31-34.

[11] 刘岑,袁小会,刘兵,等.钢制单层球形容器爆破压力的计算[J].武汉工程大学学报,2016,38(3):299-306.

[12] 李清,袁小会,刘岑,等.有效试验数据对钢材机械性能分布规律的影响[J].武汉工程大学学报,2015,37(4):69-73.

[13] 刘小宁,刘岑,李清,等.钢材屈服与抗拉强度的分布规律和参数研究[J].制造业自动化,2015(17):56-59.

[14] 刘小宁,刘岑，张红卫,等.对“基于实测数据的特种球形压力容器爆破压力计算公式”一文的商榷[J].应用数学和力学,2016,37(5):542-550.

[15] 刘小宁,刘岑,刘兵,等.屈强比对容器爆破压力计算公式精度的影响[J].应用力学学报,2017,34(1):142-148.

[16] 杨帆,刘岑,刘兵,等.钢制薄壁容器爆破压力计算公式评价[J].现代制造工程,2016,38(11):124-128.

HomogeneityIdentificationofSteelTensileTestData

Liu Cen1Yang Fan2Wu Yuanxiang2Liu Bing2Zhang Lei2Zhang Hongwei2

(1.Hubei Light Industry Technology Institute, Wuhan 430070，Hubei; 2.Wuhan Vocational College of Software and Engineering, Wuhan 430205, Hubei)

The tensile test data of homogeneity lay as the basis of examination of steel mechanical properties. Identifying the homogeneity of test data， while excluding invalid data is the premise of analyzing whether the tensile test data is homogeneous. This paper established the discriminating method of homogeneity of test data by applying mathematical statistics. Based on the data of tensile test of steel for bridges Q420NHY (medium thick plate), the homogeneity data is discriminated and the mechanical properties of the Q420NHY steel were determined when confidence was 99% on both sides. The research indicated that the influence of the homogeneity of tensile test data on the mechanical properties of steel could not be neglected.

tensile test data; mechanical properties; homogeneity; mathematical statistics; discriminate; Q420NHY steel

TH140

A

1671-3524(2017)02-0017-03

(责任编辑：李文英)

2017-04-23

湖北省教育厅科研项目(B2016545)；武汉市黄鹤英才(教育)计划

刘 岑(1989～)，女，工学硕士，助教.E-mail：104742579@qq.com