基于应力应变曲线类型的邓肯张模型修正
2017-10-24沈启鹏吴道祥胡雪婷郭佳诚孟祥龙魏东权
沈启鹏, 吴道祥, 胡雪婷, 郭佳诚, 孟祥龙, 魏东权
(1.合肥工业大学 资源与环境工程学院,安徽 合肥 230009; 2.安徽省交通规划设计研究总院股份有限公司,安徽 合肥 230088)
基于应力应变曲线类型的邓肯张模型修正
沈启鹏1,2, 吴道祥1, 胡雪婷1,2, 郭佳诚1, 孟祥龙1, 魏东权1
(1.合肥工业大学 资源与环境工程学院,安徽 合肥 230009; 2.安徽省交通规划设计研究总院股份有限公司,安徽 合肥 230088)
邓肯张模型应用于钙质结核土三轴试验的分析时,发现部分应力应变曲线不能有效地被预测。文章基于本构模型所具有的特性,结合土的结构性及应力应变曲线的特性,分析本构方程参量的作用并引进能有效描述S型应力-应变曲线的参量(密实点D为切线弹性模量为最大值时对应的应力应变点)。通过推广邓肯张模型、建立和修正反正切模型,结合钙质结核土应力应变曲线类型,探究本构模型各自的实用性与适应范围。结果表明:应用于应变硬化的反正切修正模型与邓肯张修正模型,由于变量的增加,而使得对应力-应变曲线的拟合度有所增加;邓肯张修正模型适应于反映应变软化岩土的性质,但其表现岩土物理性质的形式随着参量增加而更加复杂;反正切修正模型能较为简单地体现S型应力应变曲线的性质,表达密实点D的位置。
反正切;邓肯张;修正模型;S型应力应变曲线;密实点
在岩土力学计算分析中,为描述岩土的任何一个物理演变过程,除了需要适应于任何材料的物理定律(力的平衡方程和位移协调方程)外,还要满足与具体岩土相对应的本构模型[1]。本构模型作为嫁接应力场和应变场的桥梁,泛指各种表明状态与变量之间关系的单值方程,如反映材料力学性质的弹性模型、邓肯张模型、蠕变模型,反映材料热学性质的傅里叶热传导定律、克拉伯龙理想气体定律等,因此其是研究岩土物理力学性质的必要工具,也是区分岩土材料性质的依据[2]。
岩土的力学性质不仅受到自身密度、孔隙度、含水率、颗粒级配、矿物成分等固有性质的影响,而且受到应力路径、应力水平、应变程度等外界环境影响,无法建立一个能全面考虑各种性质和因素的理想模型,即使建立了理想模型,在模型求解过程中需要获取的岩土体自身参数和外界环境参数的量是非常多的,甚至部分参数目前还无法有效地获取[3],因此在分析岩土应力应变状态时应抓住其应力-应变的主要特征,忽略次要影响因素。目前,岩土的本构模型主要包括弹性模型、弹塑性模型、黏弹塑性模型3种,在精度方面,黏弹塑性模型能较好地反映土的变形特征和内部机理以及土体的硬化软化和剪胀性质,弹塑性模型次之,具有广阔的发展前景[4]。但非线性弹性模型略去塑性变形、应力路径和第二主应力等因素的影响作用,求解公式简单、实用,适应于工程计算分析[5]。康纳等根据大量土的三轴压缩实验结果,提出用双曲线拟合发生应变硬化的应力-应变曲线。Duncan等人据此提出了被广泛应用的增量弹性模型,即邓肯张模型,因其模型简单、概念清楚,8个参数均有对应的物理与几何意义,并可以通过常规三轴压缩实验获得[6]。然而当荷载较高时,计算沉降值偏差较大;模型对体变难以准确预测,泊松比值误差较大等诸如此类模型本身具有的缺陷[7]。
应变硬化的应力-应变曲线用指数函数A(1-e-Bx)拟合效果也较好,而与双曲线拟合效果相比,当初始弹性模量与极限偏差应力相同时,应力应变曲线变化趋势略有差别。此外含水率较低的钙质结核土或碎石土会呈现出S型应力应变曲线与应变软化,关于此方面的研究不多[8]。钙质结核土是淮北平原广泛分布的一种区域性特殊土,土层中含有大量的大小不一、形状各异、分布形式多样的钙质结核[8]。
1 定义密实点
对于含水率为18%的钙质结核土的常规三轴压缩实验,其应力应变曲线呈现S型。S型应力应变曲线各阶段图如图1所示,结合其变形特征,将其划分为4个阶段,并引入密实点D,即挤密阶段与弹性阶段分界点,此时密实点的切线模量最大,记为ED。
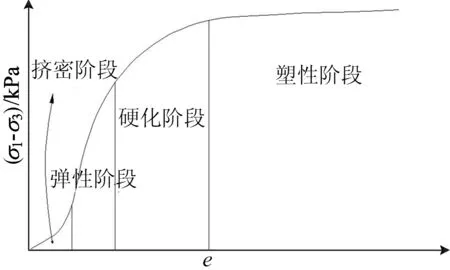
图1 S型应力应变曲线各阶段图
(1) 挤密阶段。剪应力增幅渐渐增大,变形主要为颗粒角度调整,颗粒间没有相对的滑移。
(2) 弹性变形阶段。应力-应变呈直线关系,变形主要为颗粒排列方式改变,颗粒未有破坏面。
(3) 硬化阶段。剪应力增幅渐渐降低,局部剪切破坏面开始形成,颗粒间部分发生滑移。
(4) 理想塑性阶段。剪应力增幅很小,表现为曲线趋平。剪切破坏面已经完全形成[9]。
2 邓肯张模型推广
土具有结构性和散体性等特点,应力场与应变场之间的关系是复杂的、多变的。在描述其之间关系时,需要人为设定有物理与几何意义的参数(如弹性模量、极限偏差应力等),表示应力场与应变场在变化过程中某一特定时刻存在的关系。本构模型与物理参数之间关系如图2所示,可以看出,本构模型包含的参量越多,所表达的应力场-应变场关系与实际岩土所具有的应力场-应变场关系相一致的性质越多,则其反映应力场与应变场之间的关系越精准[10]。

2.1 系数推广
邓肯张模型只容纳初始弹性模量与极限主应力差2个物理参数,不适应于反映应变软化岩土的性质。经过大量的试验与理论研究,众多学者提出在原有邓肯张模型基础上添加参量c,修正邓肯张模型,使其可以体现部分岩土体特有的软化性质,即

(1)
其中,a、b、c为与试验有关的常数[11]。
将邓肯张修正模型与邓肯张模型相比较,发现修正模型的公式在形式上等同于邓肯张模型乘上一个系数(为双曲线函数)。当a与b值相同时,比较曲线变化趋势,通过计算发现两者切线斜率只相差一个系数,同样为一双曲线函数,具体如下:
F(x)=[a+(2c-b)x]/(a+bx)
(2)
c与b大小不同时,系数与应变之间关系如图3所示。邓肯张修正模型中a与b参量值相同、c大小不同时,主应力差与应变关系图如图4所示。由图3、图4结合(1)式、(2)式可以发现:
(1) 当c (2) 当c=b时,系数恒等于1,修正模型变成邓肯张模型。 (3) 当c>b时,修正模型曲线比邓肯张模型曲线的切线斜率递减速度减缓[12]。 图3 c、b大小不同时系数与应变关系 图4 邓肯张修正模型中c不同时主应力差与应变关系 通过分析可以发现,增加系数不会导致模型的初始弹性模量改变,极限主应力差一直存在并仅与增加参量b值有关,改变的是曲线的变化趋势。本文提出了邓肯张修正模型的一般公式,即邓肯张通用模型为: (3) 在对其导数计算过程中发现:① 导数的表达式随着参量的增加越加复杂,而且对具有物理意义的参数也难以表示;② 理论上存在S型曲线,但需要满足条件较多,而且表示密实点D的表达式较为复杂。 2.2 导数推广 对于邓肯张模型,切线模量Et为: (4) 在忽略分母中次要影响因子2abε并积分、调整之后,得到能较好反映应变硬化性质的反正切函数,即 σ1-σ3=a×arctan(bε) (5) 从中不难求解出初始弹性模量为ab、极限应力差为πa/2,从而也可得到类似于邓肯张的其他参数[13]。反正切函数是一个呈S型的奇函数,移动坐标轴可以使曲线用于反映S型应力-应变曲线特征。具体过程[14]为添加一参量c使bε变为bε+c,并减去a×arctanc,称之为反正切修正模型,即 σ1-σ3=aarctan(bε+c)-aarctanc (6) 其中,a、b、c为试验所得常数。 反正切修正模型中,a与b值相同,c不同时,主应力差与应变关系如图5所示。 图5 反正切修正模型中c不同时主应力差与应变关系 从图5可以发现,当c>0时,模型为应变硬化型,c值使曲线切线斜率递减速度变得可控;当c=0时,还原为反正切模型;当c<0时,模型也为应变硬化型,但线型略有不同,呈S型,密实点为-c/b,并且切线模量最大为ab[15]。 3.1 应变硬化曲线 应变硬化型的三轴试验曲线及不同本构模型拟合曲线如图6所示。钙质结核土三轴试验参数用W18~L2-3~H15~B150表示,含水率为18%,结核粒径为2~3 cm,结核体积分数为15%,结核围压为150 kPa。从图6可以看出,邓肯张模型与反正切模型对于应变硬化的应力-应变曲线的预测效果总体较好,局部略有差别。而修正模型、反正切修正模型则能有效地反映,但反正切修正模型为获取更高的拟合度而使得参量取值较大,且可浮动范围也较大。 (a) W18~L2-3~H15~B150 (b) W18~L3-5~H06~B200图6 应变硬化曲线与拟合曲线 3.2 S型应力应变曲线 S型三轴试验曲线及不同本构模型拟合曲线如图7所示。从图7中可以发现,邓肯张模型与反正切模型对于S型应力应变曲线不能作出有效预测。而修正模型尽管从理论上可以拟合S型应力-应变曲线,但由于其需要满足条件较为苛刻而一般难以反映S型应力-应变曲线特点。反正切修正模型则能有效地预测S型应力应变曲线。 图7 S型应力-应变曲线与拟合曲线 3.3 应变软化曲线 应变软化曲线及不同本构模型拟合曲线如图8所示,选用的试样参数为W18~L3-5~H15~B200。从图8可以发现,邓肯张模型、反正切模型及反正切修正模型对于应变软化曲线不能作出有效预测;邓肯张修正模型可以贴切地反映应变软化的变化过程,并且对于应变软化所具有的各个特征能够简单地表达。 图8 应变软化曲线与不同本构模型拟合曲线图 不同应变软化曲线及邓肯张修正模型拟合曲线如图9所示。 图9 应变软化曲线与邓肯张修正模型拟合曲线 图9中,3组实验参数从上向下依次为W18~L1-2~H09~B100、W18~L2-3~H15~B50和W18~L1-2~H03~B50。不难看出,当峰值后曲线存在拐点时,邓肯张修正模型对此不能有效地反映,依据上述参量与物理参数之间关系可知,这是由于邓肯张修正模型本身只包含3个参量,并有各自对应的物理参数。因此要描述拐点的存在需要增加参量,但邓肯张通用模型中参量的增加,各物理参数表达式复杂程度也随之增加。 本文定义新参数密实点,将S型应力应变曲线分为4个阶段;从系数和导数2个方面修正邓肯张模型,使其可以适应于新线型;从应变硬化、S型曲线和应变软化,相比较得出邓肯张模型、反正切模型、修正模型和反正切修正模型分别适应的范围。 [1] 孟志敏.膨胀性应变软化土体工程特性研究[J].湖南交通科技,2008,34(2):119-122. [2] 陆广,罗周全,史秀志,等.基于邓肯张模型多参数协调的强度折减法研究[J].矿冶工程,2016,36(2):6-10. [3] 肖伦斌,张训忠.邓肯-张模型对砂卵石土适用性的试验研究[J].建筑科学,2010,26(7):1-4. [4] 谢定义,齐吉琳.考虑土结构性的本构关系[J].土木工程学报,2000,33(4):35-41. [5] JOHNSON G R,COOK W H.A constitutive model and data for metals subjected to large strains,high strain rates and high temperatures[C]//Proceedings of the 7th International Symposiumon Bauistics.[S.l.:s.n.],1983:541-547. [6] 邵东琛.一种改进邓肯张模型及其在土石坝数值模拟中的应用[J].三峡大学学报(自然科学版),2015,37(4):21-24. [7] 孙陶,高希章.考虑土体剪胀性和应变软化性的K-G模型[J].岩土力学,2005,26(9):1369-1373. [8] 吴道祥,蓝天鹏,刘秋燕,等.土的结构研究现状与展望[J].合肥工业大学学报(自然科学版),2009,32(12):1904-1910. [9] 蓝天鹏,吴道祥,杨远杰,等.钙质结核土及其大型直剪试验研究[J].合肥工业大学学报(自然科学版),2012,35(2):257-261. [10] BAZANT Z P,BELYTSCHKO T B,CHANG T P .Continuum theory for strain-softening[J].Journal of Engineering Mechanics,1984,110(12):1666-1692. [11] 王水林,郑宏,刘泉声,等.应变软化岩体分析原理及其应用[J].岩土力学,2014,35(3):609-622. [12] 王立忠,赵志远,李玲玲.考虑土体结构性的修正邓肯-张模型[J].水利学报,2004,35(1):83-89. [13] 雷国辉,陈晶晶.无黏性土剪胀性的细观认识[J].岩土工程学报,2011(9):1333-1339. [14] STEINBERG D J,COCHRAN S G,GUINAN M W.A constitutive model for metals applicable at high-strain rate[J].Journal of Applied Physics,1980,51(3):1498-1504. [15] 许家雄,曾开华,张常光.考虑中间主应力、剪胀和受扰影响的砂土新邓肯-张模型[J].铁道建筑,2012(12):83-85. Duncan-Changmodelmodificationbasedonstress-straincurvetype SHEN Qipeng1,2, WU Daoxiang1, HU Xueting1,2, GUO Jiacheng1, MENG Xianglong1, WEI Dongquan1 (1.School of Resources and Environmental Engineering, Hefei University of Technology, Hefei 230009, China; 2.Anhui Transport Consulting and Design Institute Co., Ltd., Hefei 230088, China) When Duncan-Chang model was applied to the analysis of three axis test of calcareous soil, it was found that some stress-strain curves could not be predicted effectively. On account of the characteristics of constitutive model, and in view of the soil structure and the characteristics of stress-strain curves, the function of the constitutive equation parameters is analyzed and the parameters which can effectively describe the stress-strain curves of S type are introduced(density point D is the corresponding strain when the tangent elastic modulus is the maximum). By generalizing the Duncan-Chang model, establishing and modifying the arctangent model and considering the type of stress-strain curves of calcareous nodules, the practicability and adaptability of the constitutive model are explored. The results show that the arctangent correction model and Duncan-Chang correction model which are applied to strain hardening make the fitting degree of stress-strain curve increased due to the increase of variables; Duncan-Chang correction model is adapted to reflect the properties of strain softening of rock and soil, but the physical properties of rock and soil expressed by it are more complex with the increase of parameters; the arctangent correction model can simply reflect the character of S type stress-strain curve and express the position of density point D. arctangent; Duncan-Chang; modified model; S type stress-strain curve; density point 2017-01-23; 2017-03-10 国家自然科学基金资助项目(41002117;40872190);合肥工业大学2015年省级大学生创新创业训练计划资助项目(2015CXCYS099)和合肥工业大学2017年校级大学生创新创业训练计划资助项目(2017CXCY351) 沈启鹏(1992-),男,江苏徐州人,合肥工业大学硕士生; 吴道祥(1975-),男,湖北洪湖人,合肥工业大学副教授,硕士生导师. 10.3969/j.issn.1003-5060.2017.09.022 TU411.7 A 1003-5060(2017)09-1264-05 (责任编辑 马国锋)

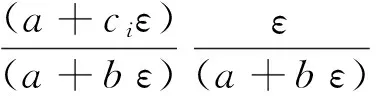


3 模型比较





4 结 论
