基于MPC的无人驾驶车辆的轨迹跟踪
2017-10-24郝亮李金良荣同康邓乐康
郝亮,李金良,荣同康,邓乐康
(辽宁工业大学汽车与交通工程学院,辽宁 锦州 121001)
基于MPC的无人驾驶车辆的轨迹跟踪
郝亮,李金良,荣同康,邓乐康
(辽宁工业大学汽车与交通工程学院,辽宁 锦州 121001)
为了更加好的实现线性时变模型预测控制算法的低速直线轨迹跟踪控制效果验证,该文采用Matlab/Simulink搭建基于运动学模型的线性时变模型预测控制算法,通过实际曲线与理想曲线仿真对比分析,从而有效证明该控制算法能够保证无人驾驶车辆在一定工况下具有良好的稳定性和安全性,为无人驾驶车辆轨迹跟踪控制算法的研究奠定了一定的基础。
线性时变;模型预测控制算法;低速直线轨迹跟踪;运动学模型
前言
随着计算机信息处理技术、传感器技术和车辆控制技术的进展,基于高效环境感知的辅助驾驶技术或全自动驾驶技术迅速发展,以主动控制为核心的先进车辆安全技术必将是现代交通系统和未来高度智能化交通系统的核心技术之一[1][2]。实现全自主无人驾驶车辆在高速和冰雪等复杂路面安全稳定的轨迹跟踪控制具有十分重要的意义,由于线性时变模型预测控制算法相比于非线性模型预测控制算法具有计算简单、实时性好等优点[3],因此,通过MATLAB/Simulink搭建基于运动学模型的线性时变模型预测控制算法,研究在给定工况下的轨迹跟踪特性,具有较强的理论研究价值与应用意义。
1 线性时变模型预测控制原理
以线性状态控制模型为基础,依次推导模型预测控制的预测方程、优化求解及反馈机制[4]。
(1)预测方程
首先,考虑一下离散线性化模型:


可以得到一个新的状态空间表达式:

式中各矩阵的定义如下:

为了进一步简化计算,做出如下假设:

如果系统预测时域为Np,控制时域为Nc,那么,预测时域内的状态量和系统输出量可以用下式计算:
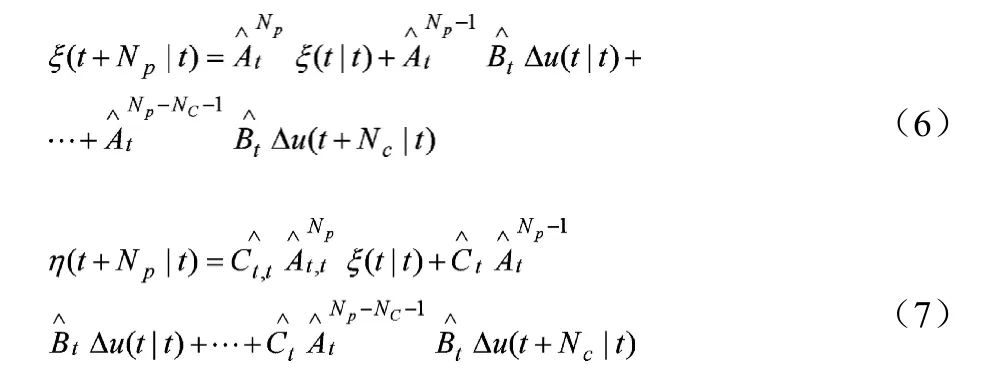
为了使整个关系更加明确,将系统未来时刻的输出以矩阵的形式表达:

式中:

通过观察式(8),可以清楚的看到,在预测时域内的状态量和输出量都可以通过系统当前的状态量ξ(t|t)和控制时域内的控制增量△U(t)计算得到。这也就是模型预测控制算法中“预测”功能的实现。
(2)优化求解
实际上,系统的控制量是未知的,只有通过设定合适的优化目标,并对其进行求解,才能得到时域内的控制序列。目标函数为:

对于以上形式的优化目标,可以通过适当的处理将其转换为二次规划问题。二次规划是一个典型的数学优化问题。它的优化目标是二次实函数,带有线性或者非线性约束。其常用的解法为有效集法和内点法。有效集法适用于解决只有不等式约束的二次规划问题,而内点法适用于任何形式的二次规划问题。
式(9)中以控制量作为目标函数中的状态量,结构简单,易于实现;但也存在一些缺点,比较显著的就是没法对控制增量进行精确约束。当系统对于控制量跳变要求较为严格时,这样的目标函数就无能为力了。此时,可以把控制增量作为目标函数的状态量,优化目标函数可以设为如下形式:

其中,第一项反映了系统对参考轨迹的跟随能力,第二项反映了对控制量平稳的变化要求。Q和R为权重矩阵,整个表达式的功能是使系统能够尽快且平稳地跟踪上期望轨迹。同时,在实际的控制系统中,往往需要满足系统状态量及控制量的一些约束条件,一般如下:
控制量约束:

控制增量约束:

输出约束:

(3)反馈控制
在每个控制周期内完成对式(12)求解后,得到了控制时域内的一系列控制输入增量:
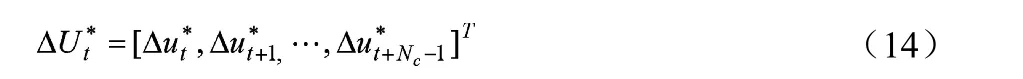
根据模型预测控制的基本原理,将该控制序列中第一个元素作为实际的控制输入增量作用于系统,即:

系统执行这一控制量直到下一时刻。在新的时刻,系统根据状态信息重新预测下一阶段时域的输出,通过优化过程得到一个新的控制增量序列。如此循环往复,直至系统完成控制过程。
2 线性时变模型预测控制仿真
2.1 Matlab仿真条件
无人驾驶车辆从坐标原点出发,以期望纵向速度v=1m/s跟踪一条直线轨迹y=3,采样时间为50ms,仿真总时间设定为20s。
2.2 低速运动学模型线性化处理
由于控制目标是无人驾驶车辆在低速情况下的跟踪控制,因此考虑以车辆运动学方程作为预测模型,低速情况下的车辆运动学方程形式如下[5]:

对其进行线性化,得到线性时变模型为:

式中,各矩阵和状态变量为:

然后按照线性时变模型预测控制原理步骤编译轨迹跟踪程序对轨迹跟踪过程进行仿真,得到仿真结果如图1-图4所示。
2.3 仿真结果
由图1可以看出实际轨迹从原点出发能够跟踪上真实直线轨迹y=3;由图2和图3可知,车辆的横向、纵向位移和前轮偏角均能很好的跟踪理想轨迹,最终达到稳定状态;由图4可知,无人驾驶的控制量纵向速度和角速度均能最终达到稳定的状态。

图1 跟踪理想轨迹的实际运行结果

图2 系统状态量随时间变化

图3 状态量偏差随时间变化
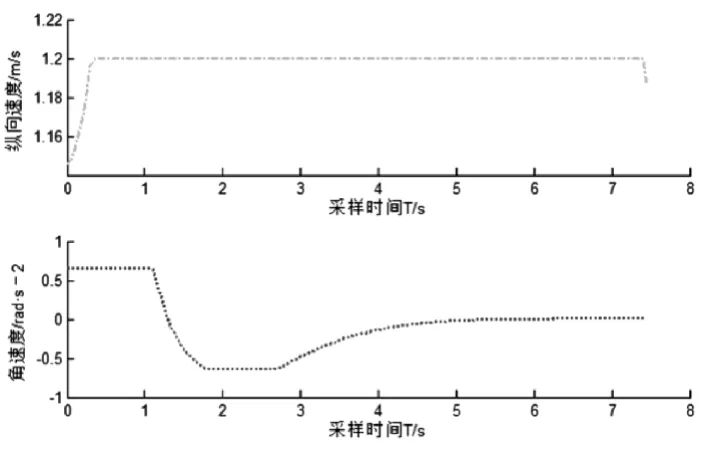
图4 控制量随时间变化
3 结论
建立的线性时变模型预测控制算法能够有效的实时跟踪车辆行驶轨迹,无人驾驶的状态量和控制量均能很好的反映出来车辆在跟踪过程中,无人驾驶车辆实际状态量均能实时跟踪理想的状态量实时状态变化,最终达到稳定状态,控制量也经过一定变化达到最终的稳定状态,这说明在低速跟踪过程中,线性时变模型预测控制算法能够实时跟踪车辆的行驶轨迹,并且保证车辆行驶过程中的实时性和稳定性。
[1] 李波.人在回路的无人驾驶车辆启发式全局路径规划算法研究[D].北京:北京理工大学,2013.
[2] 曾志文,卢惠民,张辉,等.基于模型预测控制的移动机器人轨迹跟踪[J].控制工程,2011,(S1):80-85.
[3] 任慧荣.类车移动机器人轨迹跟踪控制方法研究[D].天津:天津大学,2008.
[4] 宋金泽,戴斌,单恩忠,等.融合动力学约束的自动平行泊车轨迹生成方法[J].中南大学学报:自然科学版,2009,40(1):135-141.
[5] Zhang H,Gong J,Jiang Y,et al.An Iterative Quadratic Regulator Based Trajectory Tracking Controller for Wheeled Mobile Robot[J].Journal of Zhejiang University SCIENCE:Computer & Electro-nics,2012,13(8):593-600.
Unmanned vehicle trajectory tracking based on model predictive control
Hao Liang, Li Ginliang, Rong Tongkang, Deng Lekang
( Automobile & Traffic Engineering College, Liaoning University of Technology, Liaoning Jinzhou 121001 )
In order to validate low speed line trajectory tracking control effect of linear time-varying model predictive control algorithm,matlab simulink software is adopt to build linear time-varying model predictive control algotithm based on kinematics model. The control algorithm can ensure unmanned vehicle to possess good stability and security depended on the actual and ideal simulation curves contrastive analysis under some working condition,so it may lay a certain foundation on unmanned vehicle trajectory tracking control algorithm study.
linear time-varing; model predictive control algotithm; low speed line trajectory tracking; kinematics model CLC NO.: U467.1 Document Code: A Article ID: 1671-7988 (2017)20-53-03
U467.1 文献标识码:A 文章编号:1671-7988 (2017)20-53-03
10.16638/j.cnki.1671-7988.2017.20.018
李金良(1995-),就读于辽宁工业大学,主要研究领域为车辆系统动力学与控制,新能源汽车仿真与控制。郝亮(1979-),博士研究生,讲师。就职于辽宁工业大学。主要研究领域为车辆系统动力学与控制,新能源汽车仿真与控制。项目基金:辽宁省教育厅重大科技平台科技项目(JP2016011);辽宁工业大学大学生创新创业项目(201701027)。
