催化转化器内部瞬态流动过程CFD分析

梅德纯，刘智鑫，涂立志，张宏春

（1.江苏省交通技师学院，江苏 镇江 212028；2.江苏大学汽车与交通工程学院，江苏 镇江 212013）

设计研究

催化转化器内部瞬态流动过程CFD分析

梅德纯1，刘智鑫2，涂立志2，张宏春1

（1.江苏省交通技师学院，江苏 镇江 212028；2.江苏大学汽车与交通工程学院，江苏 镇江 212013）

运用计算流体力学(computational fluid dynamics, CFD)方法分析了催化转化器内部瞬态流场的变化。结果表明：沿催化转化器载体轴向，由于入口处壁面的影响及尾部发生边界层分离，在进出口处分别出现两个气流速度低峰；在载体某一截面径向方向上，气流速度和温度都呈现中央高而边缘低的分布；由于固相热导率和热容量大，催化转化器固相上的温度变化很小；在一个工作循环中，随着曲轴转角变化，由于管壁处形成的漩涡区，催化转化器中气流均匀性系数先降低后升高，而由于流动阻力的影响，压力损失先上升后下降。研究可为催化转化器设计及性能分析提供依据与参考。

催化转化器；流固耦合；流场；热应力

CLC NO.: U464 Document Code: A Article ID: 1671-7988 (2017)20-03-05

引言

三效催化转化器(Three way convertor, TWC)可以高效地将发动机排放的CO、HC和NOx等有害物转化为无害物质，是满足日益严格排放法规的重要的机外净化装置。净化器是排气系统中的高温元件，其内部流动的均匀性及高温尾气产生的热应力极大地影响着净化器的转换效率及工作可靠性。

目前对于净化器的 CFD研究主要集中于其内部稳态流场的数值模拟，对流场结构、速度分布及压力损失等进行分析，但很少考虑实时瞬态条件下的流动特性。净化器内高温瞬态流动将产生热变形和热冲击，对净化器使用寿命有较大影响。本文对瞬态条件下净化器内流动过程进行CFD模拟，分析其瞬态特性，为优化净化器性能提供依据与参考。

1 模型与前处理

1.1 催化转化器模型

诸多大小相同的孔道(如三角形、正方形、圆形及波纹形)构成了催化转化器蜂窝陶瓷载体[1]。通过三维模拟各管道内流场分布，可以精确得到载体内部气流的运动情况，但很难流动计算三维网格为400目/inch2的载体管道。从工程角度看，更注重载体的整体性能及对气流的影响[2]。因此，采用当量连续法，即孔道内的气流在载体内看作是连续分布[3]，研究催化转化器内部气流的分布情况。净化器的几何尺寸如图1所示。

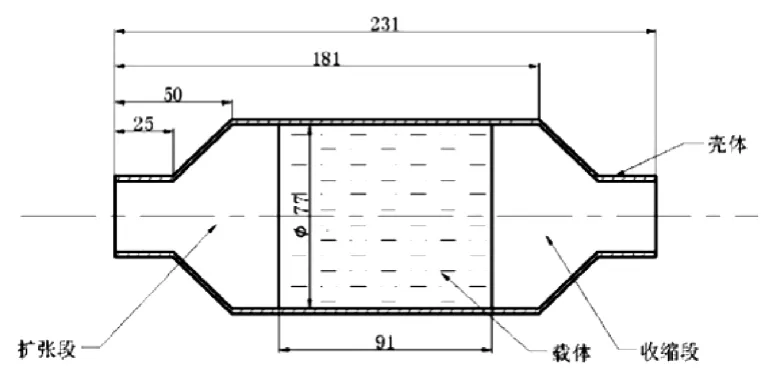
图1 净化器几何模型参数Fig.1 Geometric parameters of the catalytic convertor

依据图1的净化器几何尺寸，使用Pro/E建立催化转化器三维模型，然后划分六面体网格，如图2所示。由于模型简单规则，采用建立块(Block)的方法生成六面体网格，此方法的优势在于可生成高质量的结构网格，并且可以通过节点数和比率灵活控制边界层网格数量。该模型的节点与单元数目分别为 241564和 231040。通过网格质量检查发现Determinant(2×2×2)在0.7-1之间，该模型的网格质量很好，能够满足计算要求。

图2 净化器三维网格划分Fig.2 3D meshing of catalytic convertors

1.2 边界条件设定

以188F汽油机为研究对象，其排量为389ml，标定功率为6.2kW（3000r/min）。净化器内部气体流动遵守质量守恒、动量及能量守恒定律。采用k-ε模型求解湍流方程。考虑排气压力波动，计算时间0.32 s（即8个循环），前7个循环用于保证计算收敛，而最后一个循环用于结果输出[4]。具体模拟参数设置见表1，如图3所示的催化转化器入口处压力和温度实时数据，作为模拟计算的入口边界条件。

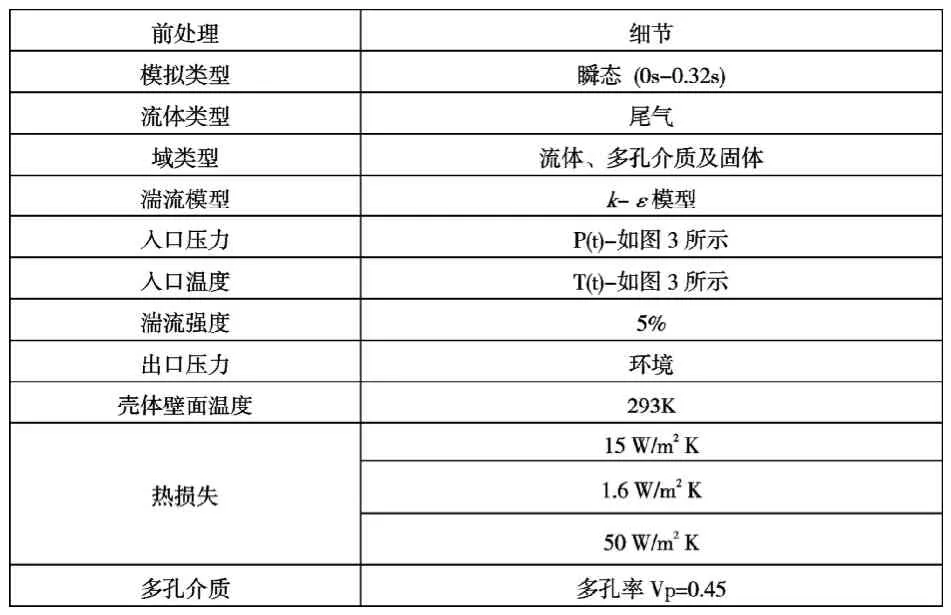
表1 模拟计算参数设置Tab.1 Parameters setting for numeric calculation

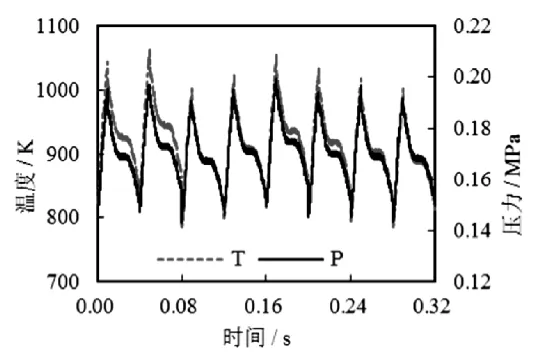
图3 净化器入口瞬时速度和温度Fig.3 Transient velocity and temperature conditions at the convertor inlet

2 催化转化器瞬态拟分析

2.1 模型有效性验证

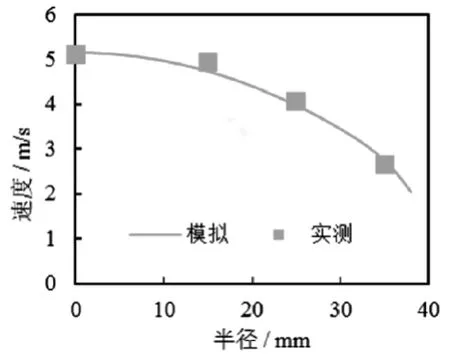
图4 距入口处176mm处速度实测值与计算值Fig.4 Themeasured velocity and the calculated one at the point of 176 mm from the inlet

图4描述了载体后端径向速度分布的试验值与模拟值的对比情况。在标定工况下，在距离进化器入口 176mm的截面上，以静压法分别测量了距离中心 0mm、15mm、25mm和35mm等测点的速度值。从图中可以明显看到，模拟值与试验值变化规律保持一致，即呈现中间流速高边缘流速低的态势，整体趋势吻合较好并且相对误差小于10%。说明催化转化器的三维模型能够较好地反应真实气体流动情况，建立的催化转化器流动数学模型是可靠的。模拟值与测量值之间的存在误差主要与计算模型以及测量误差等有关。

2.2 瞬态流场分析

图5描述了180°范围内不同曲轴转角内催化转化器内部流速、温度和压力轴向分布情况。其中，0.280s、0.282s、0.284s、0.286s、0.288s和0.290s分别对应第8个循环下0°CA、36°CA、72°CA、108°CA、144°CA、和 180°CA。选择 0-180°CA 而非一个循环，是由于在180°CA内出现波动压力的峰值。由速度分布图 5(a)可见，在扩张管壁面附近出现了漩涡区，该漩涡的存在增加了催化转化器内部流场的不均匀性，增加了压力损失。由压力分布图5(b)可见，载体前端存在压力峰值并且压力通过载体层层递减。当t=0.280 s时，载体前端的最高静压不明显，但随着入口压力的增加，该处的静压急剧增加，高静压区的存在导致了载体前端疲劳损坏，降低载体前端的使用寿命。由温度分布图 5(c)可见，温度分布受流速分布影响，温度分布情况与流速分布相似，载体中心前温度较高，原因在于高温气流直接冲刷载体前端。随着时间的推移，高温逐步扩散到载体中心后方以及收缩管处并且轴向和径向向外传送热流，温度倾向于均匀。

(a) 速度分布(b)压力分布(c) 温度分布

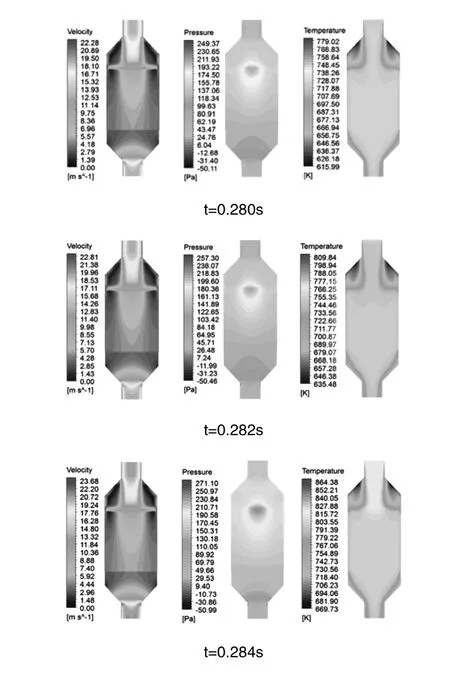
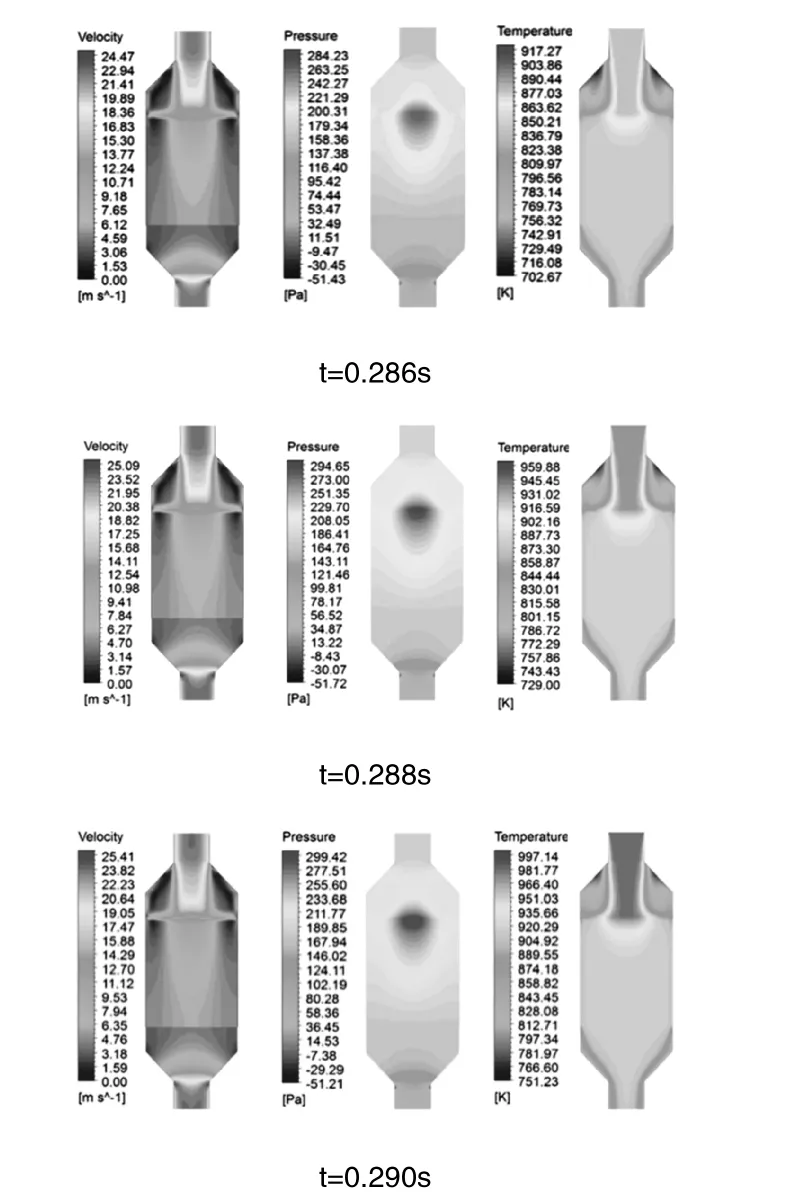
图5 不同时刻净化器内部流速、温度和压力轴向分布情况Fig.5 Distributions of flow velocity, temperature and pressure at various moments

为了更加详细地探究净化器内的瞬态流动特性，通过观察催化转化器轴向与径向速度分布，在催化转化器中心轴线上均匀取点100个，得到180°CA范围内不同曲轴转角下的速度分布情况，如图6所示。由图6(a)可见：进入催化转化器的尾气速度快速下降，在载体前端达到第一个低峰；在载体部分时速度略有增加，从载体部分出来后降至第二个低峰；随后逐渐回升直至稍高于入口速度。第一个低峰的形成是由于尾气撞到载体前端面处产生速度下降；第二个低峰的形成是由于在载体的尾迹出现了边界层分离，由于漩涡区引起了速度下降。图 6(b)描述了180°CA范围内不同曲轴转角下，载体前端10mm处催化转化器内部气流径向速度分布情况。由此可知，气流分布极不均匀，呈现出中间流速高，边缘流速低的趋势，随着时间的推移，此趋势保持不变(与文献[5]结论一致)。另外，近壁流速较高(与文献[6]结论一致)，出现此现象的原因在于：进入催化转化器的气流在通过涡旋区时被挤压，在来流与涡流相互的剪切作用下，部分中心气流在涡流区时产生分离，从而进入边缘通道。

图7描述了180°CA范围内不同曲轴转角下，催化转化器轴向压力分布情况。由图8可知，压力峰值出现在载体前端，并且随着来流压力的增大，其在载体中出现的压力峰值明也显增大。此时存在较大的压力损失，意味着催化转化器的空气动力学性能较差，影响发动机的动力性与经济性。

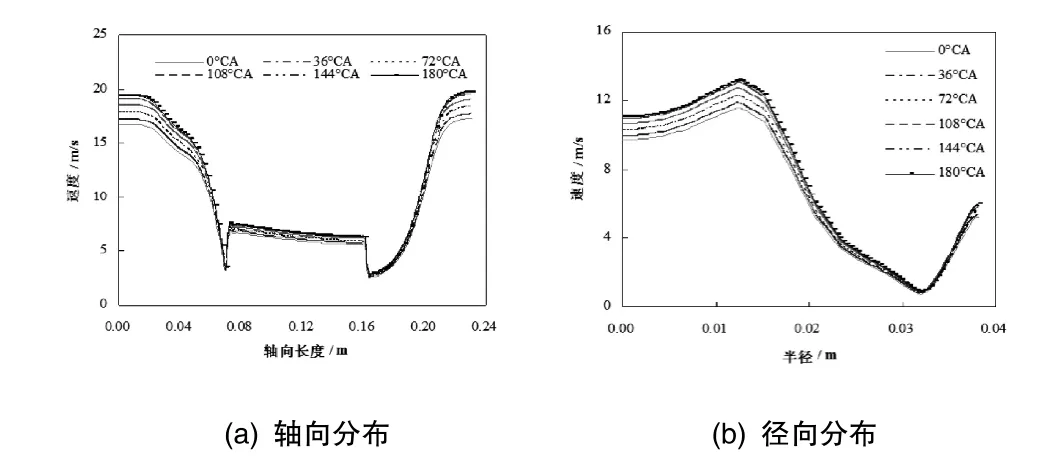
图6 不同曲轴转角下净化器内的速度分布Fig.6 Velocity distribution in the catalytic convertor at various crank angles

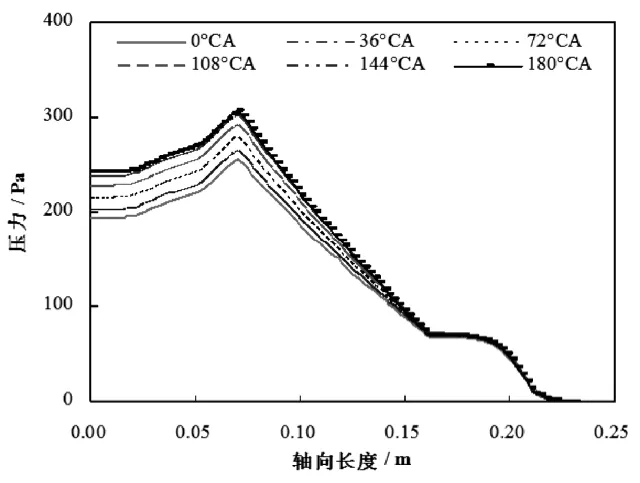
图7 不同曲轴转角下净化器内轴向压力分布Fig.7 Axil distribution of pressure in the catalytic convertor at various crank angles

图8描述了180°CA范围内不同曲轴转角下，催化转化器轴向和径向温度分布情况。从图 8(a)可知，当入口气流温度为782.4K(0°CA情况下)时，传到固体壁面上仅有740.8K，这是由于气流通过多孔介质时属于强迫对流传热并且壁面存在粘性阻力所致。从图8(b)可知，中心温度高于边缘温度，并且呈现抛物线状(与文献[7]结论一致)。除此之外，由图8 (a)和8(b)可知，气相温度变化很明显，而固相温度变化很小。

当热流量、材料的厚度及传热面积不变时，导热温差与热导率成反比[8]。事实上，这是由于固相的热导率和热容量远远高于气相。固体域良好的保温效果加快了尾气在壁面发生的催化反应，有利于提高尾气的转化效率。

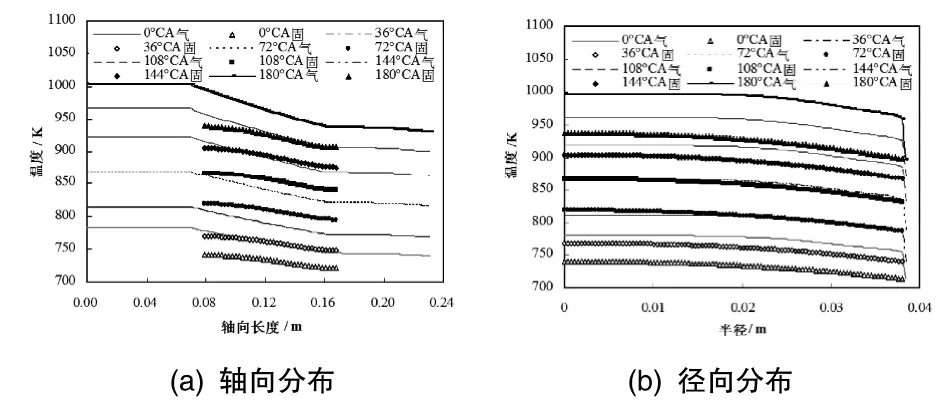
图8 净化器内的气相和固相温度分布Fig.8 Temperature distributions of gas and solid in the catalytic convertors

2.3 流动均匀性

催化转化器的压降与载体前端气流均匀性系数是两个重要的性能指标。仅仅依靠观察图5的速度云图不能定量表达速度的均匀性特征，需要引入速度均匀性系数如下[9]：

式中：x为均匀性系数，其变化范围是[0，1] (0表示只有一个计算点有值，其余的值均为0； 1表示理想的均匀流)，n为取值点的个数；vi、vmean分别为第i个取值点的流速和所有取值点流速的平均值。

计算一个循环(0-720°CA)中每度曲轴转角下所对应的均匀性系数以及压降，如图9所示。由图9可见随着压力峰值逐步逼近，均匀性系数呈下降趋势，在172°CA时出现最低，随后呈上升趋势。出现此现象的原因在于：扩张管处形成的涡流的强烈程度取决于进入催化转化器内尾气的流速，流速越高均匀性越差，而流速趋势与入口压力波的趋势相符。相反，压降随着曲轴转角增加，呈现先上升后下降的势态。原因在于：入口压力越大在载体内所产生的流动阻力就越大，能量损失就越多，根据伯努利方程可知，压降也就越大。综上所述，在一个循环下压力降与均匀系数均随时间变化而变化，呈现波动状态。可以推断，在高速大负荷下，此状态更加明显，均匀性系数的差距也会愈发明显。

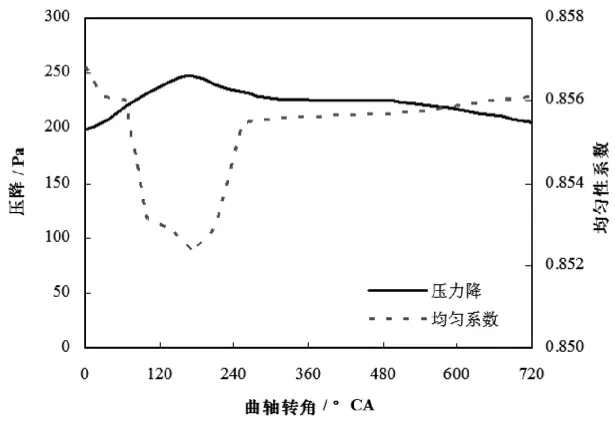
图9 一个循环下压力降与均匀系数Fig.9 Pressure drop in the catalytic convertor and its uniformity coefficient in a cycle

3 结论

运用 CFD仿真模拟分析了发动机尾气净化器内部气流的瞬态流动过程，得出以下结论：

（1）在三效催化转化器内，由于载体前端入口处壁面影响及尾端发生边界层分离，在载体入口及出口处均出现轴向速度突降，载体内部气流轴向速度较为稳定；载体内部径向气流速度分布呈现中间高、边缘低的趋势，但在近壁处，由于部分中心气流分离形成涡旋后挤压进入边缘通道而使流速增高。

（2）受流速分布影响，高温中心位于载体前端，径向温度呈现处中间高、边缘低的趋势，轴向温度逐渐降低；由于固相热导率和热容量远远高于气相，所以气相温度沿轴向或径向变化明显，而固相温度变化较小。

（3）在一个瞬态周期内，随着入口流速增加，催化转化器扩张管壁面形成的涡流增强，流动阻力增大，气流均匀性变差，当排气压力出现峰值时(172°CA时)，气流均匀性系数最低。

[1] 孙键,赵玮霖,张叶成,等. 汽车尾气催化转化器载体及涂层的结构形貌[J]. 重庆工学院学报(自然科学),2008,22(8)：11-13.(Sun Jian,Zhao Wei-lin,Zhang Ye-cheng,et al. Structural images of catalytic support and coatingfor automobile exhaust gas purifying system[J]. Journal of Chongqing Institute of Technology(Natural Science),2008,22(8)：11-13.)

[2] 帅石金,王建昕,庄人隽.车用催化转化器流场的数值模拟[J].小型内燃机,2000,29(5)：23-26.(Shuai Shi-jin,Wang Jian-xin,ZhuangRen-jun. Numerical simula-tion of automotive catalytic converters[J].Small Internal Combus-tion Engine,2000,29(5)：23-26.)

[3] 梅德纯,高为群,刘志鑫. 催化转化器内单孔道化学反应的研究[J].小型内燃机与摩托车,2013,42(6)：29-32.(Mei De-chun,Gao Wei-qun,Liu Zhi-xin. The research of chemical reactions of single span way in catalytic converter[J].Small Internal Combustion Engine And Motorcycle,2013,42(6)：29-32.)

[4] 范晓梅,许勇, 杨群立, 等. 发动机排气压力波性能仿真分析[J].计算机仿真,2010, 27(2)： 282-285.(Fan Xiao-mei,XuYong,Yang Qun-li,et al.Simulationand analysiso fangine exhaust pressure wave[J],Computer Simulation,2010, 27(2)：282-285.)

[5] ShuaiShi-jin,Wang Jian-xin. Unsteady temperature fields of mono-liths in catalytic converters[J]. Chemical Engineering Journal, 2004(100)：95-107.

[6] Chakravarthy V K, Conklin J C, Daw C S, et al. Multi-dimensional simulations of cold-start transients in a catalytic converter under steady inflow conditions[J]. Applied Catalysis A：General：2003 (241)：289-306.

[7] GaoXi,Zhu Ya-ping,LuoZheng-hong. CFD modeling of gas flow in porous medium and catalytic coupling reaction from carbon monoxide to diethyl oxalate in fixed-bed reactors[J]. Chemical Enginee-ring Science,2011(66)：6028-6038.

[8] 钱多德,姚炜.汽油机排气歧管内流场 CFD 模拟[J].内燃机与动力装置,2010,119(5)：30-32.(QianDuo-de,Yao Wei.The CFD simulationof interior flowfor gasoline engine exhaust manifold[J].Internal Combustion Engine&Powerplant,2010,119(5)：30-32.)

[9] 邓帮林,刘敬平,杨靖,等.基于双向流固耦合的汽油机排气歧管热应力分析[J].内燃机学报,2011,29(6)：549-554.(Deng Bang-lin,Liu Jing-ping,Yang Jing,et al.Thermal stress analy-sis of gasoline engine exhaust manifold based on two-way FSI [J].Transactions of CSICE,2011,29(6)：549-554.)

Analysis of the Transient Flow Processinthe Catalyst Convertor Based on CFD

Mei Dechun1, Liu Zhixin2, Tu Lizhi2, Zhang Hongchun1
( 1. Jiangsu Jiaotong College, Zhenjiang 212028; 2. School of Auto & Traffic Engineering,Jiangsu University, Zhenjiang 212013 )

The transient flow distribution ina catalytic convertor is comprehensively analyzed with employing computational fluid dynamics.The simulationresults show that the axial flow velocity in the carrierof the catalytic converteris relatively stable, howevertwo low velocity peaks come out near the entrance and outlet of the carrier respectively, which are due to the wall effects at the front entrance and the boundary layer separation at the outlet. At one given section in the carrier, in radial the velocity and temperature tend to decline from the center to the edge of wall. The temperature of the solid phase changes little due to its’ high thermal conductivity and capacity. In a working cycle, the pressure drop increases first and then decreases with the increase of crank angle due to vortex zones formed at the wall while the coefficient of uniformity is just opposite owing to flow resistance. The results above can providea favorable basis and reference for the designof catalyst converter as well as its’s performance analysis.

Catalytic converter; Fluid structure interaction simulation; Flow distribution; Thermal stress

U464 文献标志码：A 文章编号：1671-7988 (2017)20-03-05

10.16638/j.cnki.1671-7988.2017.20.002

梅德纯（1976-），男，江苏仪征人，研究生，高级讲师，主要研究方向：汽车排放控制与主动安全技术。

国家自然科学基金项目（51506101）；江苏交通运输科技项目（2016T13）。