反对称Spin-1/2阻挫钻石链的基态和磁化行为研究∗

赵阳 齐岩† 杜安 刘佳 肖瑞 单莹 吴忧 杨思浩

1)(大连民族大学物理与材料工程学院,大连 116600)

2)(东北大学物理系,沈阳 110819)

反对称Spin-1/2阻挫钻石链的基态和磁化行为研究∗

赵阳1)齐岩1)†杜安2)‡刘佳1)肖瑞1)单莹1)吴忧1)杨思浩1)

1)(大连民族大学物理与材料工程学院,大连 116600)

2)(东北大学物理系,沈阳 110819)

对含有次近邻节点自旋交换耦合的自旋-1/2伊辛-海森伯钻石链体系进行了研究,利用矩阵对角化和传递矩阵方法对基态磁相和宏观热力学量进行了严格求解,重点探讨了所有交换耦合均为反铁磁耦合时,体系节点伊辛自旋间次近邻相互作用的影响.研究结果表明次近邻节点伊辛自旋存在反铁磁耦合时会增强系统的阻挫效应,引入破坏平移对称性的经典亚铁磁相,使基态呈现出上上上下上上的自旋构型以及磁化曲线新颖的2/3磁化平台,丰富了体系的基态相图和宏观磁性行为.

伊辛-海森伯模型,传递矩阵,严格解,基态相图

1 引 言

低维量子自旋系统由于新颖的基态相以及丰富的磁学行为,在过去的三十年受到了广泛研究,其中具有钻石链拓扑结构的量子海森伯模型备受研究者的青睐［1−3］.1996年,Takano等［4］首次从理论上预测了自旋S=1/2钻石链自旋体系基态存在奇特的二聚化-单态相和四聚化-二聚态相.这一发现促进了对具有钻石形结构单元的一维量子自旋模型的研究,以期对这类体系的阻挫磁性行为获得更深刻的理解.通过零场基态性质的计算,研究者一致认同自旋-1/2扭曲钻石链海森伯模型存在复杂的基态相图,由亚铁磁相、多个量子二聚态和元格态组成［5］.

最近实验上在绝缘磁性材料Cu3(CO3)2(OH)2中取得了突破性进展,引起了理论工作者的极大研究兴趣. Kikuchi等［6］指出蓝铜矿Cu3(CO3)2(OH)2是具有钻石形拓扑结构的阻挫自旋链模型材料,并通过磁化强度的高场测量获得了与理论预测定性相符的结果,包括1/3磁化平台、具有双峰结构的磁化率和磁比热曲线等.随后,理论工作者基于量子自旋模型对钻石链及其扩展体系的一系列关键物理问题进行了细致和深入的研究,包括Dzyaloshinskii-Moriya相互作用对磁化过程的影响、磁化平台现象、磁热效应、多自旋交换作用的影响以及局域磁振子激发等［7−12］.

总体而言,量子钻石链模型在数学上并不可积,因此获得其严格动力学行为及热力学性质将是一个非常难处理的问题.文献［13—21］研究发现,通过将其中部分海森伯作用键用伊辛作用键来替代,不仅能够简化模型获得体系所有热力学量的严格解,而且有助于理解相应的纯量子模型的性质,甚至能够阐明实际材料中的磁学行为,例如三金属配位聚合物,由于Dy离子高度各向异性,用低维伊辛-海森伯交替键模型可以直观地呈现出这些化合物的主要特征［22,23］.本文采用文献［13—21］提出的伊辛-海森伯交替键模型,对含多种磁耦合竞争作用的自旋-1/2阻挫钻石链系统展开细致的研究,结合严格对角化和传递矩阵解析法,对体系的基态磁有序、低温磁化行为和热力学性质进行严格解析和深入讨论.

2 理论模型与方法

考虑由钻石形结构单元构成的一维晶格体系,伊辛和海森伯两种自旋在晶格上有规律地交替排列,如图1所示,其中节点处的紫色实心圆表示伊辛自旋,间隙处的红色实心圆表示海森伯自旋.为方便起见,将系统哈密顿量表示为子单元Hi求和的形式,其中Hi对应两个海森伯自旋和一个伊辛自旋构成的结构单元能量,并涵盖了它们之间所有相互作用,表达式如下:

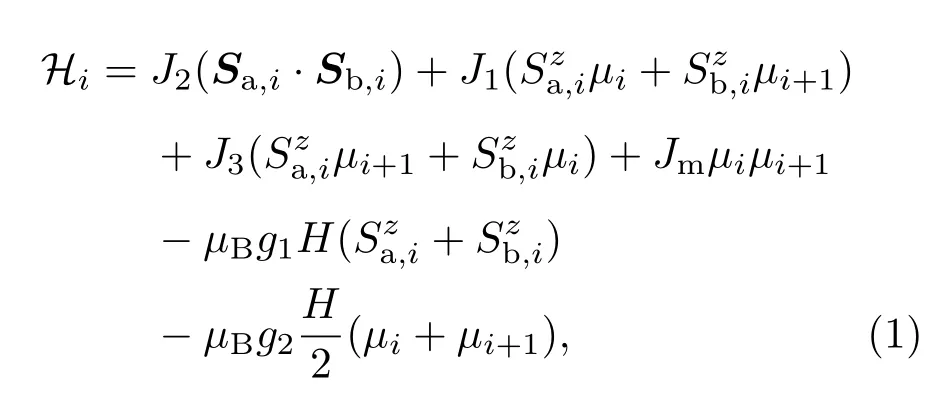
图1 (网刊彩色)伊辛-海森伯钻石链示意图 红色和紫色实心圆分别代表伊辛和海森伯自旋,J1,J2,J3,Jm代表不同的磁性键Fig.1.(color online)Sketch of the Ising-Heisenberg diamond chain.The purple and red solid circles represent the Ising and Heisenberg spins,respectively;J1,J2,J3and Jmrepresent di ff erent magnetic bonds.

其中β=1/kBT,kB为玻尔兹曼常数并取其值为1,T为绝对温度,和Trs表示对所有伊辛自旋和海森伯自旋自由度求和,Tri表示对自旋链上第i个单元内的海森伯自旋自由度求迹.从方程(2)可以很明显地看出,要进一步计算必须先处理好后面的求迹部分.为此,我们以海森伯自旋的自旋态|↑,↑〉i=|↑〉a,i|↑〉b,i,|↓,↓〉i=|↓〉a,i|↓〉b,i,|↑,↓〉i=|↑〉a,i|↓〉b,i和|↓,↑〉i=|↓〉a,i|↑〉b,i作为基矢,对哈密顿量单元Hi进行矩阵表示,并对其对角化获得如下四个能量本征值解析表达式,最终完成对海森伯自旋自由度求迹.

同时相应的本征态按照标准基{|↑↑〉,|↑↓〉,|↓↑〉,|↓↓〉}表示如下:

其中概率振幅R±的表达式为

完成对量子自由度迹的求解后,应用传递矩阵法,将系统配分函数表示成类似经典一维伊辛自旋链配分函数的形式,

这里T是一个2×2传递矩阵,Λ1,2是传递矩阵T的两个本征值,Zµi,µi+1是第i个单元中的部分配分函数:

结合方程(6)和(7)可以得到传递矩阵T的具体表达形式:

然后求解T的本征值,在热力学极限下只有最大本征值保留下来,从而一个子单元的平均自由能表示为

至此完成了对自由能的严格求解,在此基础上就可利用传递矩阵方法获得任何热力学函数的解析表达式,具体求解过程可参看文献［11—13］,这里不再赘述.

3 计算结果与讨论

3.1 基态相图

本部分对自旋−1/2阻挫钻石链体系的有趣磁学行为进行探讨和分析.考虑到阻挫作用下体系的自旋几何阻挫与局域量子涨落间的竞争作用表现得最为显著,因此着重考察所有交换耦合均为反铁磁时阻挫存在的情况,即J1,J2,J3,Jm＞0.为方便起见,选取J2作为约化单位并引进一套无量纲参数:j1=J1/J2,j3=J3/J2,jm=Jm/J2,h=µBgH/J2和t=kBT/J2.

首先讨论系统基态可能存在的自旋构型.根据哈密顿量子单元的本征值(3)式和本征态(4)式,可以构建出阻挫钻石链所有可能的基态自旋构型并求得相应的能量.考虑到自旋平移及反转对称性,在作用参数j1,j3,jm以及外磁场h的相互竞争下,该体系在基态存在五个不同的自旋构型:饱和顺磁态SP,两个经典亚铁磁态FRI1和FRI2,量子亚铁磁态QFI和量子反铁磁态QAF,具体表示如下:

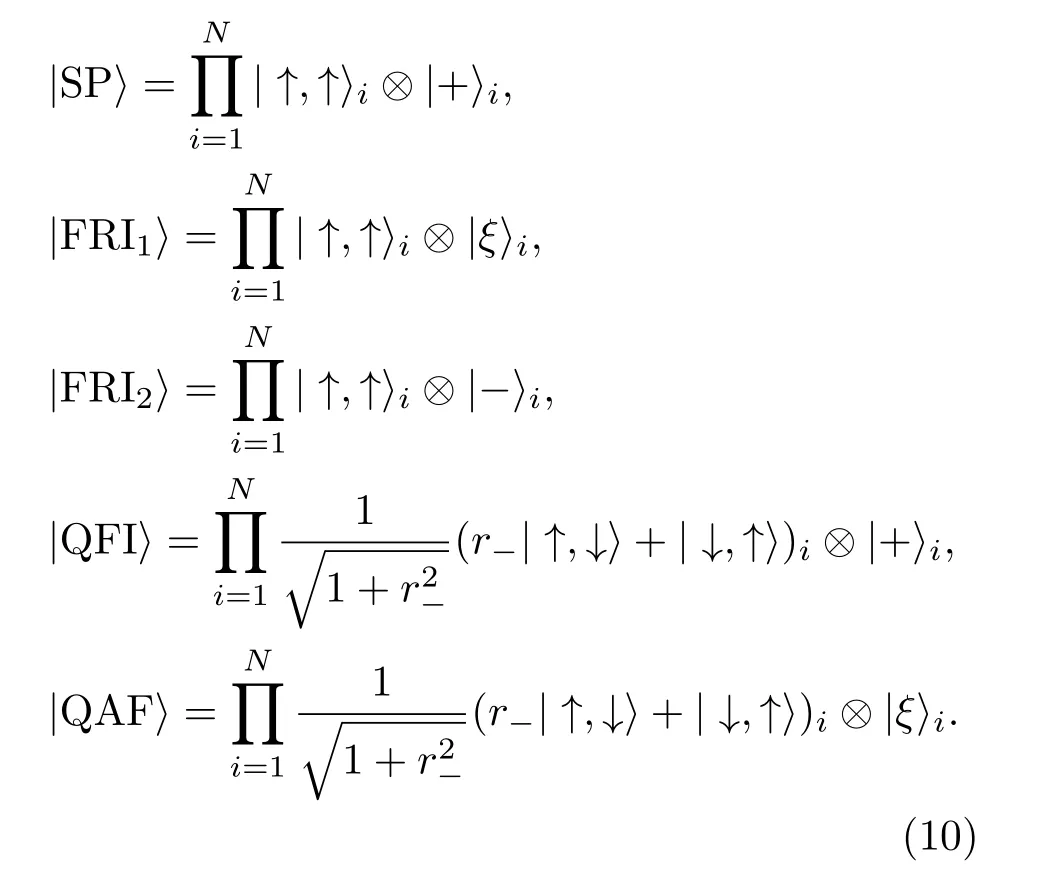
上式中刃向量|±〉i和|ξ〉i表示子单元i中节点伊辛自旋指向,与两海森伯自旋相关的态矢量则由方程(4)给出.

相应的基态能为:

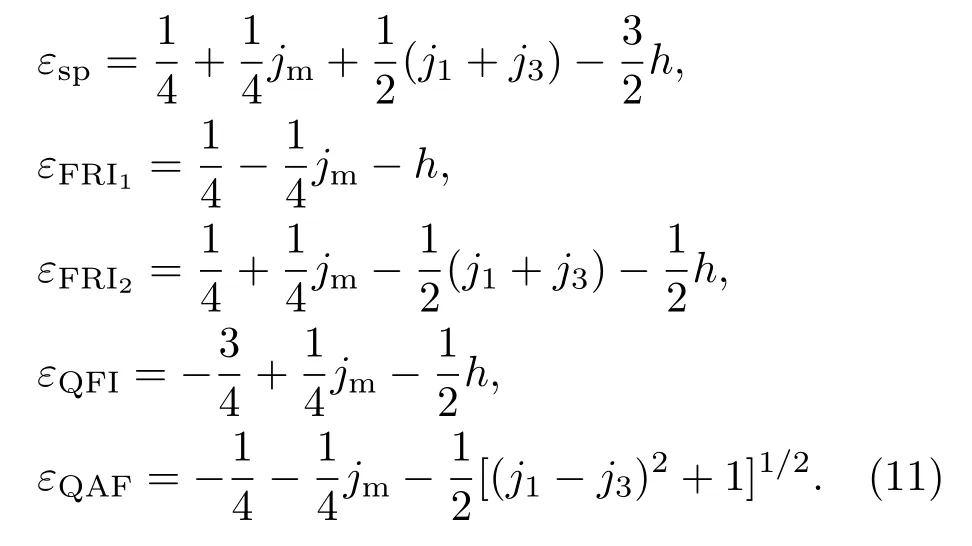
图2 jm-h平面内基态相图,其中j1=j3=1Fig.2.Ground-state phase diagram in the jm-h plane for j1=j3=1.

结合方程式(10)和(11)中给出的自旋构型和基态能,构建了阻挫钻石链体系在jm-h平面内的基态相图,如图2所示.可以看到所有可能的磁相都呈现在图中,展示了单体伊辛自旋间耦合作用的影响.同时,由于反对称交换作用j1=j3=1,使自旋态处于高度竞争,从而导致了FRI2和QFI相具有相同的能量,共同存在于相图中的同一个区域.为了简便,在后面的讨论中将该简并态简称为FQ相.由图2可知,在高磁场下,自旋处于全部极化态,均朝向外磁场方向,基态表现为饱和顺磁相SP.当磁场相对较小时,基态展现了多样化的自旋构型,具体表现为亚铁磁态(FRI1,FRI2或QFI)或独一无二的量子反铁磁态QAF.其中基态FRI2对应经典亚铁磁自旋构型,即所有海森伯自旋沿外磁场方向排列,而所有节点伊辛自旋由于它们间的反铁磁耦合反平行于外磁场方向.但当海森伯自旋间的反铁磁耦合比较强时,能量上海森伯自旋对更倾向形成单-二聚态.在这种情况下,体系将处于量子亚铁磁基态QFI,表现为伊辛自旋朝向外磁场方向,表明自旋阻挫有效地消除了近邻间隙自旋和节点自旋耦合的影响.当磁场值非常小时,节点伊辛自旋间的次近邻反铁磁耦合将引起伊辛自旋间的反铁磁排列,从而使体系基态表现为量子反铁磁态QAF.除此之外,节点自旋间的次近邻耦合还会引入不具备平移对称性的FRI1基态,具体表现为海森伯自旋朝向外磁场方向,节点伊辛自旋互相反平行排列.为了讨论的完整性,将各基态相间的边界方程列于表1中.

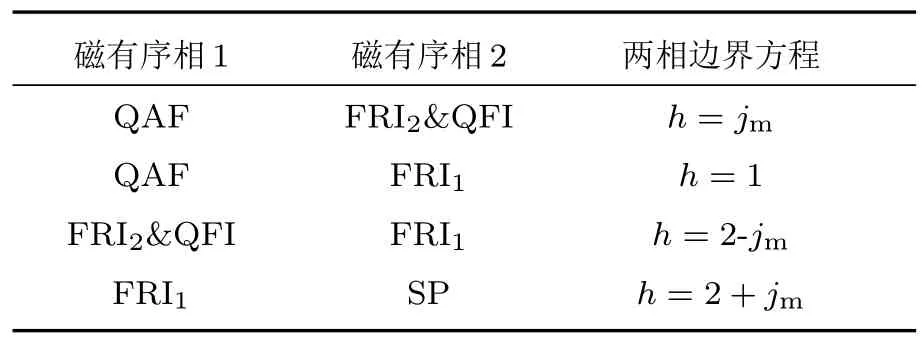
表1 边界两侧的磁有序相及边界方程Table 1.Magnetic order phases and their boundary equations.

3.2 低温磁化行为和热力学性质

基于构建的基态相图,对体系的低温磁化过程进行了分析和讨论.图3描述了典型阻挫参数jm=0.75和jm=1.25分别作用下,系统总磁化强度随外磁场的变化行为.总体上看,当系统处于零温时,所有磁场诱导的零温相变呈现陡峭的跳跃,相应磁化曲线表现为完美阶梯状.当温度为有限值时,磁化曲线开始变得平滑,并伴随着台阶宽度的收缩.对于不同伊辛自旋次近邻耦合jm,系统将经历不同的磁化路径,从而展现出不同的磁化平台,其中磁化平台的宽度对应着基态相存在的场区间.

当jm=0.75时,从图3(a)中可以看到,磁化曲线展现了1/3,2/3和1磁化平台,反映出磁场分别在临界场hc1=0.75,hc2=1.25以及hc3=2.75处诱导的连续相变QAF-FQ,FQ-FRI1和FRI1-SP.当jm=1.25时,如图3(b)所示,1/3磁化平台消失,2/3磁化平台加宽,与零温的QAF-FRI1相变相呼应.值得一提的是,由于次近邻交换耦合jm的存在,低温磁化曲线展现了与基态FRI1相密切关联的新颖的2/3磁化平台.同时,以上这些磁化平台值满足Oshikawa-Yamanaka-Affleck条件n(Stot−m)=integer,其中n表示由哈密顿量的空间结构决定的基态周期,Stot和m分别表示基本单元的总自旋和磁化强度.此外,从图中还可以看出低温磁化曲线紧密跟随零温磁化曲线,(如t=0.01时的磁化曲线),证明了图2所构建基态相图的正确性.

图4给出了与图3参数条件相同,总磁化强度在不同外磁场作用下随温度的变化行为.可以看到,当外磁场非常接近临界场时,磁化强度展现了温度引起的显著变化.当磁场略低于(高于)临界场时,磁化强度在强烈地热涨落诱导下呈现增加(减小)趋势;而当磁场的值处于相应磁化平台中间区域或是大于饱和磁场值时,磁化强度随着温度的增加呈现了稳定的下降趋势.值得注意的是当磁场处于临界场时(除了临界场hc1=0.75处),磁化强度随着温度的上升也呈现了单调递减的变化行为.

图3 当j1=j3=1时,磁化强度在不同温度下随外磁场的变化 (a)jm=0.75;(b)jm=1.25.Fig.3.The total magnetization as a function of external magnetic fi eld with j1=j3=1 at several di ff erent temperatures for two representative cases:(a)jm=0.75;(b)jm=1.25.

图4 当j1=j3=1时磁化强度在不同外磁场下随温度的变化 (a)jm=0.75;(b)jm=1.25;其中深红色菱形表示不同基态共存的临界场Fig.4.Temperature dependence of the magnetization per site with j1=j3=1 at several magnetic fi elds for two representative cases:(a)jm=0.75;(b)jm=1.25.The rhombus symbols in black red denote critical fi elds at which di ff erent ground states coexist together.

由于系统中多种磁耦合作用的存在以及钻石链本身的几何阻挫结构,因此来自不同相互作用项的能量将会产生微妙的竞争关系,从而使系统展现出丰富的热力学行为.图5给出了不同次近邻节点伊辛自旋相互作用下,零场磁比热随温度的变化曲线.由图5(a)可以看到,当jm=0时,磁比热曲线在低温区仅呈现出一个宽阔的圆形单峰.当jm存在且其值比较小时,磁比热展现出双峰结构,具体表现为极低温区的高尖峰和低温区的驼峰,表明次近邻伊辛自旋间的交换耦合增强了体系的阻挫效应,诱导了磁比热极低温区的尖峰.随着jm的增加,尖峰和驼峰峰宽加宽并互相靠拢,其中尖峰向高温区移动,驼峰则向低温区靠近.当继续增加jm,如图5(b)所示,两峰汇聚在一起形成一个圆峰,此时磁比热又恢复为单峰结构,其峰值随着jm增强而变大.磁比热曲线所展现的复杂和多样化变化行为,反映了体系自旋阻挫与温度热涨落引起的局域自旋激发态的相互竞争.

图5 不同交换耦合jm作用下零场磁比热随温度的变化,其中j1=j3=1Fig.5.Temperature variations of the zero- fi eld speci fi c heat for various exchange couplings jmunder j1=j3=1.

4 结 论

研究了节点伊辛自旋间的次近邻交换耦合对伊辛-海森伯钻石链体系的基态性质和热力学行为的影响.利用传递矩阵方法严格求解了体系的磁化强度、磁化率和磁比热,着重探讨了所有交换耦合为反铁磁时,几何阻挫和局域量子涨落相互竞争下体系有趣的磁学行为.研究结果显示,节点次近邻交换耦合的引入,丰富了体系的基态相和磁化平台,使体系展现出饱和顺磁态SP、亚铁磁态FRI1和FRI2,量子亚铁磁基态QFI以及独一无二的量子反铁磁基态QAF五个不同基态相.其中量子亚铁磁态FRI2和QFI对应着1/3磁化平台,经典亚铁磁态FRI1对应着新颖的2/3磁化平台.值得注意的是,在不考虑次近邻交换耦合时,该平台在钻石链体系中并没有出现.此外,还展示了零场磁化率和磁比热与温度间的多样化依赖关系,其中零场磁比热随次近邻伊辛反铁磁耦合的变化呈现丰富的双峰结构.

［1］Kikuchi H,Fujii Y,Chiba M,Mitsudo S,Idehara T,Kuwai T 2004J.Magn.Magn.Mater.272 900

［2］Rule K C,Wolter A U B,Süllow S,Tennant D A,Brühl A,Köhler S,Wolf B,Lang M,Schreuer J 2008Phys.Rev.Lett.100 117202

［3］Jeschke H,Opahle I,Kandpal H,Valentí R,Das H,Dasgupta T S,Janson O,Rosner H,Brühl A,Wolf B,Lang M,Richter J,Hu S,Wang X,Peters R,Pruschke T,Honecker A 2011Phys.Rev.Lett.106 217201

［4］Takano K,Kubo K,Sakamoto H 1996J.Phys.:Condens.Matter8 6405

［5］Okamoto K,Tonegawa T,Kaburagi M 2003J.Phys.:Condens.Matter15 5979

［6］Kikuchi H,Fujii Y,Chiba M,Mitsudo S,Idehara T,Tonegawa T,Okamoto K,Sakai T,Kuwai T,Ohta H 2005Phys.Rev.Lett.94 227201

［7］Ivanov N B,Richter J,Schulenburg J 2009Phys.Rev.B79 104412

［8］Aimo F,Krämer S,Klanjšek M,Horvatić M,Berthier C 2011Phys.Rev.B84 012401

［9］Takano K,Suzuki H,Hida K 2009Phys.Rev.B80 104410

［10］Gu B,Su G 2007Phys.Rev.B75 174437

［11］Verkholyak T,Strečka J 2013Phys.Rev.B88 134419

［12］Pereira M S S,de Moura F A B F,Lyra M L 2008Phys.Rev.B77 024402

［13］Rojas O,de Souza S M,Ohanyan V,Khurshudyan M 2011Phys.Rev.B83 094430

［14］Pereira M S S,de Moura F A B F,Lyra M L 2009Phys.Rev.B79 054427

［15］Strečka J,Jaščur M 2003J.Phys.:Condens.Matter15 4519

［16］Čanová L,Strečka J,Jaščur M 2006J.Phys.:Condens.Matter18 4967

［17］Valverde J S,Rojas O,de Souza S M 2008J.Phys.:Condens.Matter20 345208

［18］Torrico J,Rojas M,Pereira M S S,Strečka J,Lyra M L 2016Phys.Rev.B93 014428

［19］Ohanyan V,Honecker A 2012Phys.Rev.B86 054412

［20］Hovhannisyan V V,Ananikian N S,Kenna R 2016Physica A453 116

［21］Hovhannisyan V V,Strečka J,Ananikian N S 2016J.Phys.:Condens.Matter28 085401

［22］Visinescu D,Madalan A M,Andruh M,Duhayon C,Sutter J P,Ungur L,van den Heuvel W,Chibotaru L F 2009Chem.Eur.J15 11808

［23］van den Heuvel W,Chibotaru L F 2010Phys.Rev.B82 174436

Ground-state and magnetization behavior of the frustrated spin-1/2 antisymmetric diamond chain∗

Zhao Yang1)Qi Yan1)†Du An2)‡Liu Jia1)Xiao Rui1)Shan Ying1)Wu You1)Yang Si-Hao1)
1)(School of Physics and Materials Engineering,Dalian Minzu University,Dalian 116600,China)
2)(College of Physics,Northeastern University,Shenyang 110819,China)

The low-dimensional quantum spin systems have been extensively studied in the past three decades due to the novel ground states and rich magnetic behaviors,especially the quantum spin chain with diamond topology structure.Motivated by recent experimental success in Cu3(CO3)2(OH)2compound,which is regarded as a model material of spin-1/2 diamond chain,researchers have paid a lot of attention to various variants of diamond spin chains.In this paper,we mainly examine the magnetic properties of an antisymmetric spin-1/2 Ising-Heisenberg diamond chain with the secondneighbor interaction between nodal spins.By using exact diagonalization and transfer-matrix methods,the ground-state phase diagram,magnetization behavior and macroscopic thermodynamics are exactly solved for the particular case that all magnetic bonds yield antiferromagnetic couplings,which usually shows the most interesting magnetic features closely related to a striking interplay between geometric frustration and quantum fl uctuations.To clearly illustrate the e ff ect of second-neighbor interaction item,we consider a highly frustrated situation that all Ising-Heisenberg bonds and Heisenberg bonds possess the same interaction strength.The calculation results indicate that the second-neighbor interaction item will enrich ground states and magnetization plateaus.A classical ferrimagnetic phase FRI1corresponding to a novel two-thirds of intermediate plateau with translationally broken symmetry is introduced,manifesting itself as up-up-up-down-up-up spin con fi guration at a ground-state.In addition,there are other four distinct ground states which can be identi fi ed from the phase diagram,i.e.,one saturated paramagnetic phase SP,one classical ferrimagnetic phase FRI2,one quantum ferrimagnetic phase QFI and the unique quantum antiferromagnetic phase QAF.The classical phase FRI2and quantum phase QFI both generate one-third of magnetization plateau.It is worth mentioning that all the values of these magnetization plateaus satisfy the Oshikawa-Yamanaka-Affleck condition.Besides,the results also have shown a rich variety of temperature dependence of total magnetization and speci fi c heat.The magnetization displays the remarkable thermal-induced changes as the external fi eld is sufficiently close to critical value where two or more than two di ff erent ground states coexist.At the critical fi eld relevant to a coexistence of two di ff erent states,the total magnetization displays a monotonic decrease trend.The thermal dependence of zero- fi eld speci fi c heat displays relative complex variations for di ff erent second-neighbor interactions between nodal spins.At fi rst,the speci fi c heat presents only a single rounded Schottky-type maximum.Using the second-neighbor interaction,another sharp peak arises at low-temperature and is superimposed on this round maximum,and the speci fi c heat exhibits a double-peak structure.On further strengthening,the low-temperature one keeps its height shifting towards high temperature,while the hightemperature round peak su ff ers great enhancement and moves in an opposite direction.Finally,the low temperature peak entirely merges with the Schottky-type peak at a certain value of second-neighbor interaction,and above this value,the speci fi c curve recovers its single peak structure.The observed double-peak speci fi c heat curves mainly originate from thermal excitations between the ground-state spin con fi guration QAF and the ones close enough in energy to the ground state.

Ising-Heisenberg model,transfer-matrix method,exact solution,ground-state phase diagram

14 May 2017;revised manuscript

4 July 2017)

(2017年5月14日收到;2017年7月4日收到修改稿)

10.7498/aps.66.197501

∗国家自然科学基金(批准号:11547236)、辽宁省教育厅一般项目(批准号:L2015130)、大连民族大学大学生创新创业训练计划项目(批准号:201712026371)和中央高校基本科研业务费(批准号:DC201501065,DCPY2016014)资助的课题.

†通信作者.E-mail:qiyan@dlnu.edu.cn

‡通信作者.E-mail:duan@mail.neu.edu.cn

©2017中国物理学会Chinese Physical Society

PACS:75.10.Pq,75.30.Kz,75.40.Cx

10.7498/aps.66.197501

*Project supported by the National Natural Science Foundation of China(Grant No.11547236),the General Project of the Education Department of Liaoning Province,China(Grant No.L2015130),and the Training Programs of Innovation and Entrepreneurship for Undergraduates of Dalian Minzu University,China(Grant No.201712026371),and the Fundamental Research Funds for the Central Universities,China(Grant Nos.DC201501065,DCPY2016014).

†Corresponding author.E-mail:qiyan@dlnu.edu.cn

‡Corresponding author.E-mail:duan@mail.neu.edu.cn