某车室低频噪声近似建模分析与板件优化

胡启国，王宇谦，李苏平

（1.重庆交通大学 机电与车辆工程学院，重庆 400074；2.重庆交通大学 交通运输学院，重庆 400074）

某车室低频噪声近似建模分析与板件优化

胡启国1，王宇谦1，李苏平2

（1.重庆交通大学 机电与车辆工程学院，重庆 400074；2.重庆交通大学 交通运输学院，重庆 400074）

为了降低车室低频噪声，采用对声学贡献较大的车室地板、后地板、前围板、顶棚、前车门内板及后车门内板的厚度参数为因子，以车身质量、车身模态频率、驾驶员头部处声压峰值和声压均方根值为响应，采用最优拉丁超立方试验设计方法采集样本数据进行因子空间设计。利用径向基神经网络方法，建立了4个响应关于6个因子的误差小、精度高的近似模型，并对所建立的近似模型进行误差分析。以驾驶员头部处声压峰值最小为目标函数，板件厚度参数为自变量，驾驶员头部处声压均方根值、车身质量和车身模态频率为约束条件。采用自适应模拟退火算法对板件厚度进行优化设计，其优化结果表明，驾驶员头部处最大声压峰值所在的频率158 Hz处的声压降低了4.45 dB，134 Hz处的声压峰值降低了5.47 dB，在其他声压峰值较高的频率处，测点声压均有不同程度降低，说明在满足约束条件同时，通过优化有效地降低车室空腔噪声，提高车辆的声学舒适性。

声学；低频噪声；最优拉丁超立方设计；径向基神经网络近似模型；自适应模拟退火算法；声学优化

汽车作为重要的交通工具，已成为人们日常出行不可缺少的一部分。顾客在评价车辆品质时，除了关注驾驶的稳定性和安全性外，也越来越多地关注车室的声学特性。车室空腔存在的既突出而又难以消除的低频噪声问题，是影响车室声学环境的主要原因之一。研究表明，在频率0～200 Hz范围内，车身薄壁板件受外界激励作用产生的结构辐射噪声，对车室的低频噪声贡献较大[1–2]。为降低车室噪声，提高车辆的声学舒适性，需对声学贡献较大的车身结构进行优化，但是因有限元模型规模较大，利用有限元计算方法优化会耗费很长时间，相比之下通过近似模型方法优化具有高效的特点[3]。文献[4]以板件厚度为设计变量，以驾驶员右耳处声压最小和车身质量最小为优化目标，通过响应面法建立近似模型，对车室声学环境进行了优化。文献[5]通过建立以板件振动速度和第1阶模态频率为优化目标，以板件和阻尼层厚度为设计变量的2阶响应面近似模型，进行了声振优化。通过响应面方法建立近似模型，虽然具有表达式相对简单和计算效率较高的特点，但是在样本点数量有限时，并不能保证模型的精度。而通过径向基神经网络方法建立的近似模型，不仅具有很强的逼近复杂非线性函数的能力，而且近似模型能通过所有的样本点，所建立的近似模型精度很高。

在车辆研发设计阶段，针对车室的低频噪声问题，为了能通过少量的样本点建立精度足够高的近似模型优化车室声学环境，提高声学优化效率，本文采用最优拉丁超立方设计方法采集样本数据，通过径向基神经网络方法来建立近似模型。然后基于建立的近似模型，利用自适应模拟退火算法对车身板件厚度参数进行优化设计以改善车室声学环境。这为降低车室低频噪声提供了一种可行的方法。

1 建立有限元模型

车辆车身结构复杂且多由薄壁板件构成，在Hypermesh中建立有限元模型时，以不影响车身结构主要特性为前提，对模型进行了适当简化，并利用壳单元划分网格。综合考虑计算精度和工作量，网格单元尺寸取为10 mm，建立的车身结构有限元模型共含有444 150个单元，464 592个节点。整车有限元模型如图1所示。

对车身板件围成的车室密闭空腔，利用四面体单元进行网格划分。研究表明，座椅对空腔声场的声学特性影响较大[6]，故在建立声腔有限元模型时，也建立了座椅模型。声学网格单元长度依据在每个波长内至少含有6个单元的原则，取网格单元长度为50 mm～140 mm，由此建立的空腔声场有限元模型如图2所示，其共含有四面体网格单元29 467个，节点6 229个。

图1 车身结构有限元模型

图2 空腔声场有限元模型

2 建立近似模型

在驾驶员头部D、副驾驶员头部P、后排左侧乘客头部RL和右侧乘客头部RR处分别定义一场点，作为声压响应输出点[10]。同时施加频率在0～300 Hz范围内的发动机激励力和由路面随机激励引起的悬架激励力，通过基于模态的声振耦合响应分析，发现在0～200 Hz的低频范围内，车室测点在频率158 Hz、134 Hz、198 Hz、152 Hz和78 Hz附近声压较高，测点A计权声压曲线如图3所示。

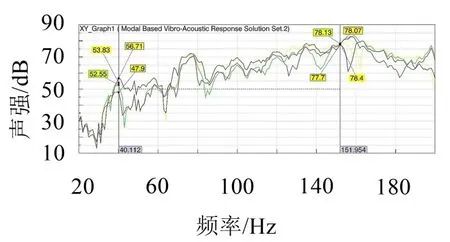
图3 四测点A计权声压曲线

经车身板件声学贡献分析，在这些声压较高的频率处发现车身地板（pshell_11001、pshell_12001）、顶棚（pshell_20001）、前围（pshell_13001）和车门内板（pshell_3102、pshell_3202）对测点声压声学贡献较大。

2.1 采集样本数据

根据板件贡献分析确定的声学贡献较大板件，试验设计以车室地板pshell_11001（t1）、后地板pshell_12001（t2），前 围 板 pshell_13001（t3），顶 棚pshell_20001（t4）、前车门内板 pshell_3102（t5）和后车门内板pshell_3202（t6）的厚度参数为因子，其设计范围均在0.5 mm≤ti≤2 mm之间。为了能通过少量的样本点建立尽可能准确的近似模型，在Isight中利用最优拉丁超立方设计[7]方法对6个因子进行试验设计，每个因子在其设计范围内取30个水平，则最优拉丁超立方设计的设计矩阵共有30个水平组合。

因驾驶员处的声压级水平是衡量车室声学环境的重要评价标准，且为在降低车室声压的同时，避免车身质量增加过大和车身第7阶模态频率过低，将车身质量、车身第7阶模态频率、驾驶员头部处D测点的声压峰值和声压均方根值作为试验设计的响应。以试验设计矩阵中的每一组水平值作为一次试验的输入参数，在Hypermesh中改变相应板件的厚度参数，并计算车身质量m；在Nastran中进行模态计算，确定每组水平值对应的第7阶模态频率sf；在Virtual.Lab中计算驾驶员头部处D测点的声压D，并利用Matlab计算D测点的声压均方根值drms。根据试验设计方案，30组试验因子水平及其所分别对应的4个响应值如表1所示。

2.2 径向基神经网络近似模型

依据试验设计采集的样本数据，以6个因子为输入参数，4个响应为输出参数，利用径向基神经网络方法[8]建立近似模型，由此建立的径向基神经网络近似模型的形状系数c为1.33。以声压峰值D关于板件厚度参数t1、t2、t3、t4、t5、t6的近似模型为例，其部分三维曲面如图4所示。

2.3 误差分析

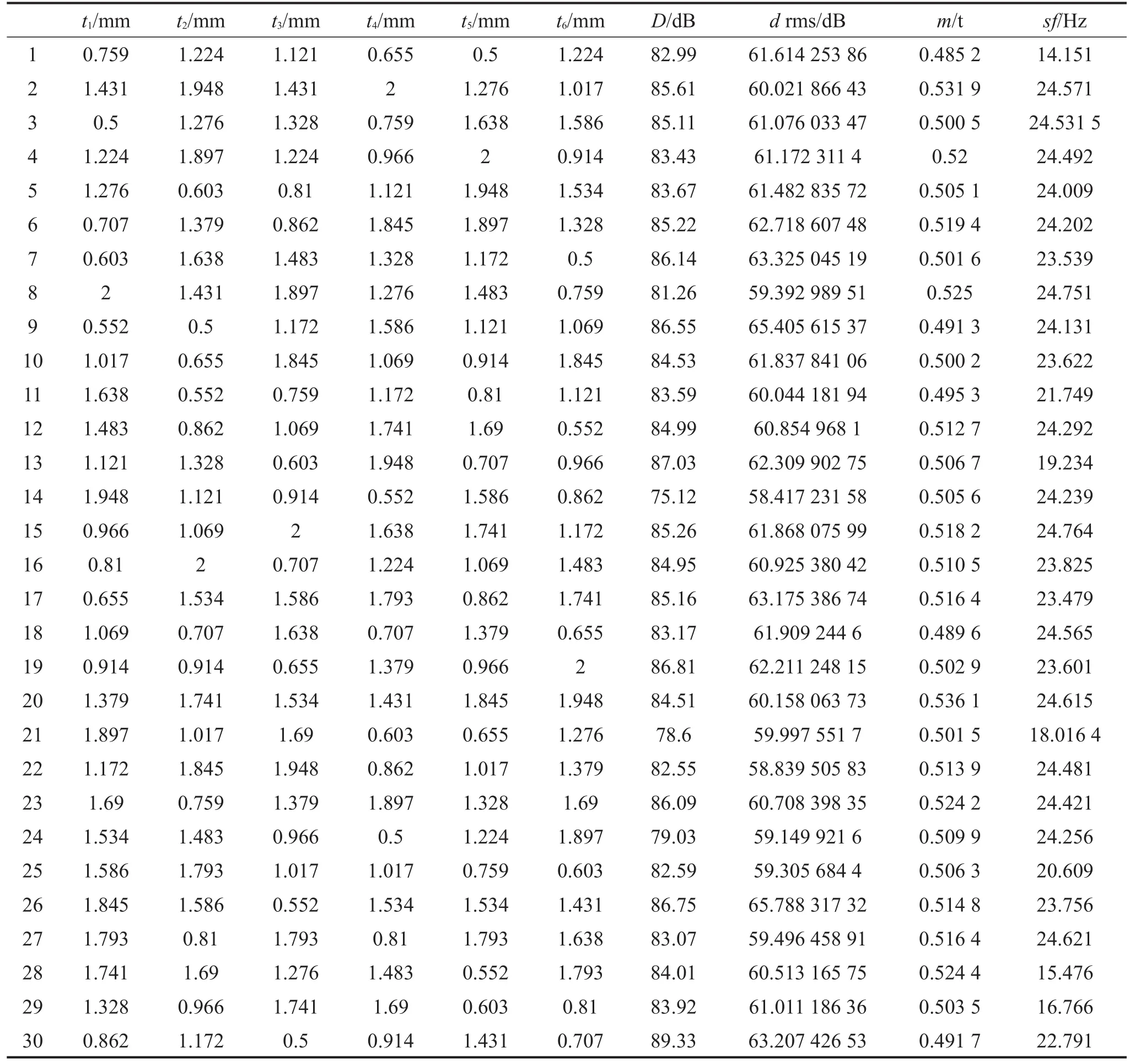
表1 样本数据

为检验所建立的径向基神经网络近似模型的准确性和可靠性，用设计变量空间的20个非插值点作为误差检查样本对近似模型进行误差分析。利用均值误差、最大误差、均方根值误差和复相关系数4个指标评价模型的精度。对于近似模型的均值误差、最大误差和均方根值误差，要求值越小越好，均值误差和均方根值误差上限为0.2，最大误差上限为0.3，而复相关系数R2则要求越大越好，下限为0.9，其值越接近于1表示模型的可信度越高。所建立的径向基神经网络模型的各项误差分析值如表2所示。

根据误差分析指标，所建立的近似模型的均值误差、最大误差和均方根值误差均远小于其误差标准，且各个输出响应的复相关系数都非常接近于1，说明模型的误差很小。

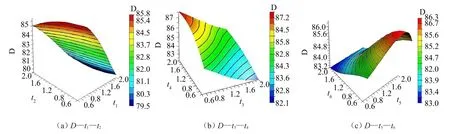
图4 声压峰值D近似模型曲面

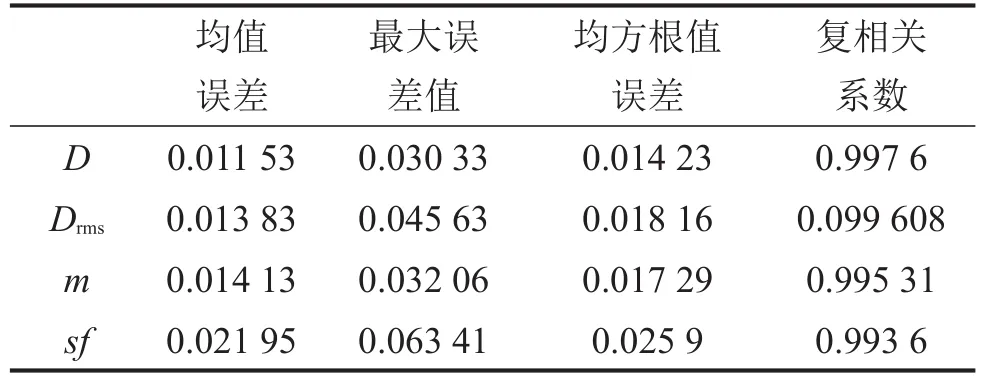
表2 误差指数分析

以误差检查样本的输入参数为相应输入，利用近似模型计算车身质量、车身第7阶模态频率、D测点声压峰值和声压均方根值的预测值。误差检查点的4个响应真实值与预测值之间的关系如图5所示。

如图5所示，经近似模型计算得到的响应预测值与真实值相差很小，进一步说明利用径向基神经网络方法建立的响应近似模型精度非常高。

综上所述，误差分析结果表明，采用最优拉丁超立方试验设计方法采集样本，利用径向基神经网络方法建立的，以板件厚度参数为输入，以车身质量、车身第7阶模态频率、D测点声压峰值和声压均方根值为输出响应的近似模型误差小、精度高，满足建模要求，可以代替有限元模型进行优化设计。

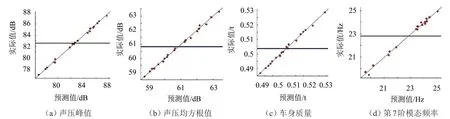
图5 误差检查点的响应真实值与预测值关系

3 优化模型

根据建立的径向基神经网络近似模型，以D测点声压峰值D最小为目标函数，以板件厚度参数t1、t2、t3、t4、t5、t6为设计变量，其取值范围为0.5 mm≤ti≤2 mm。

因为测点声压均方根值能反映车室声压的总体水平，所以为使车室声压不因车身结构的改变而升高，以D测点的声压均方根值drms≤60 dB为约束条件之一。

板件厚度参数的改变会引起车身质量的变化，考虑到车辆的轻量化设计要求，其质量必须限制在一定范围内。原设计车身结构的质量为0.480 2 t，优化设计中限制车身质量m≤0.5 t。

以车身第7阶模态频率为响应进行采样时发现，随着车身板件厚度参数的变化，车身第7阶模态主要为前车门处的局部模态，模态频率主要在集中在24 Hz左右，但是在个别因子水平组合下也存在第7阶模态频率过低的情况。若车门处模态频率过低，则易受外界载荷激励的影响使车室声压过高，所以限制车身第7阶模态频率sf必须满足条件：sf≥24 Hz。

则，优化问题的数学模型为

4 车室声学优化

4.1 最优化结果

基于建立的优化模型，利用自适应模拟退火算法[9]对板件厚度进行优化。一般较高的初始温度虽然能有效避免最优值陷入局部最优解，但会使得所需计算量庞大，降低模型接受效率[11]。本文为解决这一矛盾，采用较低的初始温度和新的退火计划，模型作局部随机扰动（在当前模型周围），以在锁定最优解空间后，由于搜索空间变小，能提高模型接受效率。新的退火计划将作适当的回火升温，这样如果当前模型没有跳出局部极小值区间，适当的升温可以使之再一次跳出，使最终解更可靠。设置初始温度为1，收敛检查间隔为5，温度参数下降的相对比率为1，温度损失函数下降比率为1，允许计算失败的最大次数为5。共经过10 112次计算，在因子设计空间得到D测点声压峰值D最小时的板件厚度参数最优值，得到相关最优化设计结果。将板件厚度参数的最优化结果四舍五入取小数点后两位，优化结果与最终取值如下表3所示。

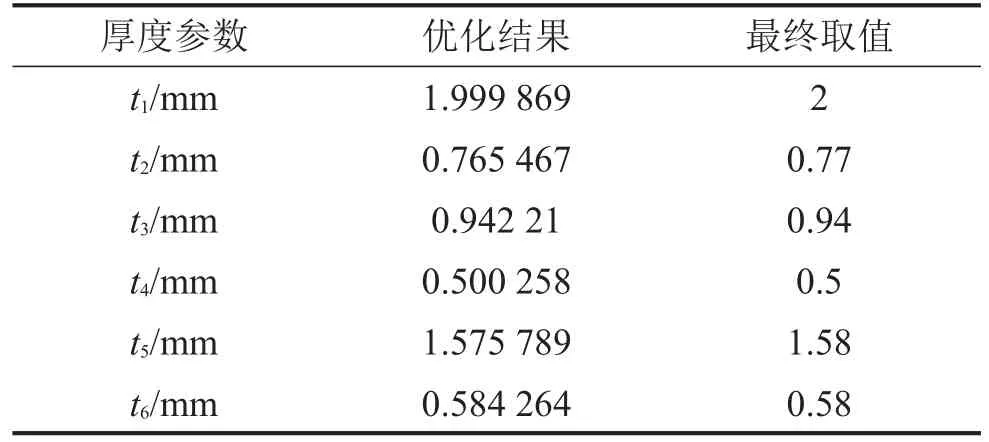
表3 优化结果与最终取值

以板件厚度参数的最终取值作为有限元模型的板件厚度，计算车身质量，车身结构模态及车室声压分布。分别采用近似模型与有限元模型计算的响应值对比如表4所示。

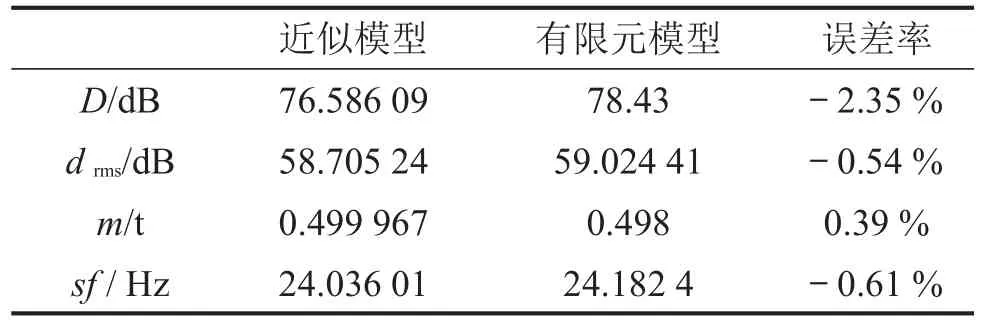
表4 响应值对比

根据表4知，由近似模型计算的响应值与有限元模型计算的响应值误差率很小，说明所建立的径向基神经网络近似模型的精度高，最优化结果具有很好的可信度。

4.2 优化前后对比

优化前后，车身板件厚度参数取值、车身质量、车身第7阶模态频率、驾驶员头部处D测点的声压峰值和声压均方根值对比见下表5。

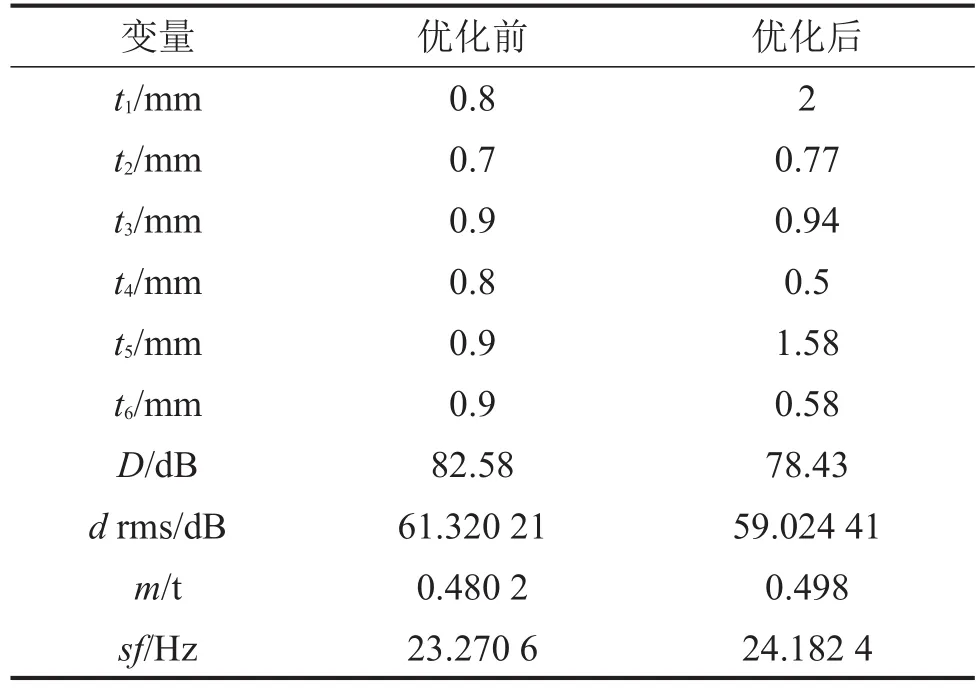
表5 优化前后对比

由表5知，经车身板件厚度参数优化，驾驶员头部处D测点的最高声压峰值降低了4.15 dB，声压均方根值降低约了2.3 dB，有效地降低了车室声压。车身质量较优化前仅增加了17.8 kg，满足轻量化设计要求。优化后车身第7阶模态频率为24.182 4 Hz，能避免车门处因存在较低的局部模态受外界激振力作用而产生辐射噪声。

为分析车身板件厚度参数优化后，车室空腔在频率20 Hz～200 Hz范围内的声压变化，将板件厚度优化前后，驾驶员头部处D测点A计权声压曲线对比如图6所示。

图6 优化前后D测点A计权声压曲线对比

如图6所示，板件厚度参数优化后，驾驶员头部处D测点声压在优化前声压较高的频率范围内均降低明显，其中最大声压峰值所在的频率158 Hz处声压降低了4.45 dB，在频率134 Hz处声压峰值降低了5.47 dB，并且在其他声压峰值较高的频率处，测点声压均有不同程度的降低，说明通过车身板件厚度优化有效地降低了车室空腔噪声，提高了车辆的声学舒适性。

5 结语

（1）采用最优拉丁超立方试验设计方法采集样本数据，利用径向基神经网络方法建立的近似模型具有误差小、精度高的特点，能作为有限元模型的替代模型对车身板件厚度参数进行优化设计。

（2）板件厚度优化后，驾驶员头部处D测点的声压均方根值降低了约2.3 dB，车身质量仅增加了17.8 kg，车身第7阶模态频率达到了24.182 4 Hz，而D测点在最大声压峰值所在的频率158 Hz处的声压降低了4.45 dB，134 Hz处的声压峰值降低了5.47 dB，在其他声压峰值较高的频率处，测点声压也均有不同程度的降低，这表明在满足各项约束条件的同时，有效地降低了车室声压，显著地提高了车室的声学舒适性。

（3）通过建立径向基神经网络近似模型，以D测点声压峰值D最小为优化目标，以板件厚度参数为设计变量，以D测点声压均方根值、车身质量和车身第7阶模态频率为约束条件，采用自适应模拟退火算法优化板件厚度参数以降低车室声压的方法，不仅可行而且有效。

[1]朱才朝，秦大同.车身结构振动与车内噪声声场耦合分析与控制[J].机械工程学报，2002，38（8）：54-58.

[2]刘禹，喻凡，柳江.车辆乘坐声固耦合模态分析[J].噪声与振动控制，2005，25（5）：38-40+67.

[3]ALEXANDER I J FORRESTER,ANDY J KEANE.Recentadvancesin surrogate-based optimization[J].Progress inAerospace Sciences,2009,45(1):50-79.

[4]臧献国.基于模态振型和响应面法的结构声学性能优化设计[D].长沙：湖南大学，2011.

[5]靳畅，周鋐.基于车内综合声场贡献分析的车身板件声振优化[J].汽车工程，2015，37（12）：1438-1444+1432.

[6]白胜勇，靳晓雄，丁玉兰，等.轿车乘坐室声学模态分析[J].同济大学学报，2000（2）：206-209.

[7]赖宇阳.Isight参数优化理论与实例详解[M].北京：北京航空航天大学出版社，2012.

[8]隋永康，宇慧平.响应面方法的改进及其对工程优化的应用[M].北京：科学出版社，2011.

[9]INGBER L.Adaptive simulated annealing（ASA）:lessons learned[J].Control and Cybernetics,1996,25:33-54.

[10]李苏平，胡启国，胡海波，等.车室低频噪声预测与车身板件声学贡献分析[J].噪声与振动控制，2016，36(4)：103-107.

[11]陈华根，吴健生，王家林，等.模拟退火算法机理研究[J].同济大学学报(自然科学版)，2004，32(6)：802-805.

Approximate ModelingAnalysis and Panel Optimization of a Vehicle Compartment for Low Frequency Noise Reduction

HU Qi-guo1,WANG Yu-qian1,LI Su-ping2
（1.School of Mechanotronics&Vehicle Engineering,Chongqing Jiaotong University,Chongqing 400074,China;2.College of Traffic&Transportation,Chongqing Jiaotong University,Chongqing 400074,China）

The problem of reduction of the low frequency noise of a vehicle compartment is studied.The thickness parameters of the panels,which have large acoustic contribution,are considered as the influencing factors,and the vehicle weight,the seventh-order modal frequency of vehicle body,the sound pressure peak and the root-mean-square value of the sound pressure near the driver’s head are considered as the responses.The optimal Latin hypercubic sampling method is applied to perform the experimental design for sampling in the factorial design space.By using the RBF(radial basis function)neutral-network method,an approximate model of four responses about six factors is established.Then,error analysis is performed on the approximate model.An optimization model is set up with minimizing the peak sound pressure near driver’s head as the object function,the thickness parameters of panels as design variable,the sound pressure rootmean-square value,the vehicle weight and the seventh-order modal frequency of the vehicle body as the constraint conditions.The adaptive simulated annealing algorithm is applied to optimize the panel’s thickness to improve the vehicle compartment acoustic environment.Optimization results show that the peak sound pressure near driver’s head is reduced by 4.45 dB at 158 Hz frequency and by 5.47 dB at 134 Hz frequency respectively.The sound pressures at the measurement points are significantly reduced.The results indicate that through the optimization the vehicle interior cavity noise is reduced effectively,and the acoustical comfort of the vehicle is improved significantly.

acoustics;low frequency noise;optimal Latin hypercubic design;RBF neutral-network approximate model;adaptive simulated annealing algorithm;acoustic optimization

O422.6

A

10.3969/j.issn.1006-1355.2017.05.021

1006-1355(2017)05-0097-06

2017-0-17

国家自然科学基金资助项目（51375519）重庆市基础科学与研究专项重点资助项目（cstc2015jcyjBX0133）；

胡启国(1968－)，男，重庆市人，教授，博士后，主要从事车辆系统动力学，机械可靠性等方面的教学与研究。

Email:swpihqg@126.com

王宇谦（1994—），女，武汉市人，硕士生，从事汽车振动与噪声分析研究。

E-mail:haqiankaka@163.com