生猪价格与母猪价格异向波动的识别与实证

李洪姝，王刚毅*，卢凤君，司润祥

（1.东北农业大学经济管理学院，黑龙江哈尔滨 150030；2.中国农业大学经济管理学院，北京 100083）

生猪价格与母猪价格异向波动的识别与实证

李洪姝1，王刚毅1*，卢凤君2，司润祥1

（1.东北农业大学经济管理学院，黑龙江哈尔滨 150030；2.中国农业大学经济管理学院，北京 100083）

为研究超常波动区间生猪价格与母猪价格（生猪价格为全国三元生猪价格，母猪价格为全国二元母猪价格）的波动关系，确定两者是否存在异向波动，本文首先引入异步系数，对数据进行基本统计分析，并通过波动幅度将价格波动划分为正常波动与超常波动；再通过互谱分析和时间序列分析进行实证。结果表明：生猪价格与母猪价格的波动密切相关，且生猪价格波动略微领先于母猪价格波动；超常波动区间下，生猪价格与母猪价格的异向波动确实存在，且异步系数稍高于正常波动区间；异向波动可以看作是生猪价格超常波动的一个表征和警兆。

生猪价格；母猪价格；异向波动；互谱分析；时间序列分析

我国是全球最大的生猪生产国和消费国，生猪产业对居民生活和经济发展具有很大的影响。生猪价格的波动具有周期性，约为35～45个月[1]，共分为下跌阶段、稳定阶段和上升阶段[2]。但2008年以后，生猪价格的周期波动逐渐丧失规律性且波动幅度加大[3]，国家为减缓价格波动，促使生猪产业健康发展，对生猪市场进行宏观调控，但收效甚微。同时，生猪市场存在价格传导效应[4]，生猪价格与其他相关产品的价格会互相影响，此方面研究较多，如魏君英等[5]研究发现仔猪价格与生猪价格的波动显著正相关且具有双向因果关系；何蒲明等[6]研究发现玉米价格与生猪价格正向相关且存在长期均衡关系，短期玉米价格对生猪价格的影响具有时滞；Saengwong等[7]通过研究确定了饲料与玉米、豆粕和生猪价格间的双向因果关系以及从玉米到生猪、饲料到生猪、豆粕到饲料的单向因果关系。现有关于生猪价格与母猪价格关系的研究较少。王利荣等[8]研究发现，能繁母猪存栏量与生猪价格存在互相影响且长期均衡的关系。母猪作为生猪生产环节的上游，母猪价格直接影响仔猪的价格和数量，影响生猪养殖成本，从而影响生猪价格；同样，生猪市场的行情也影响着母猪养殖主体的决策，进而影响母猪价格。生猪价格波动与母猪价格波动互相影响，形成恶性循环造成更大程度的波动，严重影响生猪产业的健康发展，因此研究超常波动下生猪价格与母猪价格的波动关系对于生猪产业链健康发展具有重要意义。本文将从频域和时域2个角度，对超常波动下生猪价格与母猪价格波动间的关系进行研究，对可能存在的异向波动进行识别与实证，并在此基础上，以母猪为入手点，提出稳定生猪价格波动的对策建议。

1 异向波动识别

本文通过异步系数识别生猪价格与母猪价格间的异向波动，并将异向波动分为绝对异向波动与相对异向波动。首先采用同步系数法计算生猪价格与母猪价格的绝对同步系数和相对同步系数，进而得出2种异步系数，以此对异向波动进行识别。文中选取2008年1月1日—2017年1月7日生猪价格和母猪价格的周度价格数据作为样本数据（源自布瑞克农业数据库），其中生猪价格与母猪价格的单位虽然不同，但本文所分析的是上升或下降的趋势，因此不受计量单位的影响。

1.1 绝对异向波动 绝对异向波动指数指变化方向相反的波动，绝对同步系数的计算：

其中，ASC表示绝对同步系数，n表示数据序列长度，mt表示2列数据相邻数据的变化方向，变化方向相同（相邻两期数据没有发生变化时，视为增加）[8]，mt=1 ；变化方向不同，mt=1。

绝对异步系数的计算：

通过计算得出，生猪价格序列与母猪价格序列的ASC为0.683，AAC为0.317，即生猪价格与母猪价格同时上升或下降的概率为0.683；一种价格上升，另一种价格下降的概率为0.317；在样本区间内共发生了86次绝对异向波动，通过波动持续的时间进行分段，见表1。

表1 绝对异向波动持续时间分布表

如表1所示，绝对异向波动持续时间普遍较短，持续时间2周以下的异向波动占比达86.1%，而3周以上的仅占13.9%。发生绝对异向波动的原因可能有2点：第一，相对于生猪价格，母猪价格变化存在滞后期，当生猪价格从下降变为上升时，母猪价格会在开始的一段时间依然保持下降趋势，而绝对异向波动的持续时间即为母猪价格变化的滞后期；第二，在生猪价格上升后，母猪养殖主体发现生猪获利更多，受短期利益驱使，放弃饲养母猪，供大于求，导致母猪价格下降，形成绝对异向波动。

1.2 相对异向波动 相对异向波动不仅包括数值变化方向相反的波动，还包括数值变化的加速度方向相反的波动，即一个减速上升，一个加速上升；或一个减速下降，一个加速下降。相对同步系数的计算：

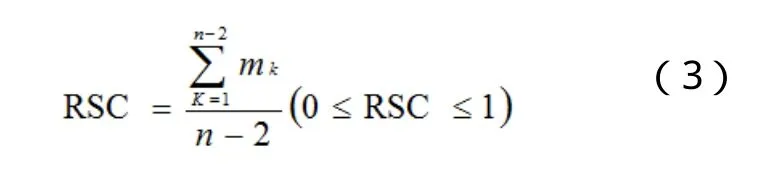
其中，RSC表示相对同步系数，n表示数据序列长度，mk表示2列数据相邻数据的变化方向及相邻数据上升或下降的加速度方向。相邻数据变化方向相反（相邻两期数据没有发生变化时，视为增加），或相邻数据变化方向相同，加速度方向相反（加速度没有发生变化时，视为增加），mk=0；相邻数据变化方向相同，加速度方向相同，mk=1。

相对异步系数的计算：

通过计算得出生猪价格序列与母猪价格序列的RSC为0.364，RAC为0.636，即生猪价格与母猪价格同时加速或减速上升（下降）的概率为0.364，其他情况的概率为0.636；在绝对异向波动的分析中得出一种价格上升，另一种价格下降的概率为0.317，所以一个减速上升一个加速上升，或一个减速下降一个加速下降的概率为0.319；在样本区间内共发生了99次相对异向波动，通过波动持续的时间进行分段，见表2。

表2 相对异向波动持续时间分布表

如表2所示，相对于绝对异向波动，相对异向波动持续时间长，持续时间2周以下的异向波动占比下降到50.5%，而3周以上的则上升到49.5%。相对异向波动发生的原因可能有以下2点：一方面，生猪价格上升，通过价格传导母猪价格也相应上涨，形成推力，另一方面，由于母猪养殖主体由于短期利益，选择养殖生猪放弃母猪，导致母猪市场供大于求，形成拉力，推拉力共同作用，形成相对异向波动；此外，生猪价格下降，生猪养殖主体对生猪市场失去信心，不愿再购买仔猪，由此造成母猪价格更快速的下降，形成相对异向波动。

1.3 异向波动与超常波动 在1.1和1.2的基础上，可以看到相对异向波动包含了绝对异向波动，因此从这部分开始，文中只对相对异向波动进行研究，并将其简称为异向波动。生猪价格波动具有周期性，一定范围内的波动属于正常现象，但从2008年开始，生猪价格的非正常波动愈加频繁，为分析生猪价格与母猪价格异向波动与超常波动的关系，首先对超常波动进行界定，对2008年1月1日—2017年1月7日生猪价格的变化进行整理。

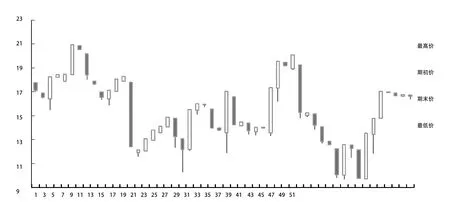
图1 生猪价格变化的K线图

如图1所示，2008年1月1日—2017年1月6日共发生52次波动，图中每一小部分表示1次波动，黑色表示波动的期初价格高于期末价格，白色柱形则表示期末价格高于期初价格，最高点与最低点的间隔代表极差，可以看到极差的跨度范围是0～6，大多分布在0～3。考虑到物价因素，先对极差进行处理， 公式如下：

k表示该次波动开始的年份

之后将调整后的极差按升序排列，人为定义后15%为超常波动，如表3所示，2008年以来生猪市场共发生8次价格超常波动。

由此将样本区间分为正常波动区间和超常波动区间，通过对超常波动区间的同步系数和异步系数的计算，得到超常波动区间的异步系数为0.66，约为同步系数的2倍，因此可以说在统计上识别出超常波动区间下存在生猪价格与母猪价格的异向波动。如表4所示，共有130周属于超常波动区间，其中发生31次异向波动，异向波动总周数为86周，分别占总样本区间的31.31%和29.55%，微高于超常波动的周数占比28.45%；同时，超常波动区间的异步系数为0.66，略高于总样本区间和正常波动区间的异步系数，因此可以看出超常波动下的异向波动更为明显。

2 实证分析

为进一步分析超常波动区间下生猪价格与母猪价格波动的相关关系，本文在这一部分通过互谱分析和Var模型对生猪价格和母猪价格之间的关系进行实证分析，确定2个变量间的相关程度以及各频率分量上超前、同步、滞后的关系，并确定变量间如何相关，进而在计量上对生猪价格与母猪价格间的异向波动进行实证。

表3 生猪价格超常波动表

2.1 数据处理 由于本文选取的是时间序列数据，需要对其进行平稳性检验。利用EVIEWS对生猪价格和母猪价格进行平稳性检验，检验结果表明，生猪价格的t值是-0.36，大于10%水平的ADF临界值-1.62，且存在单位根的概率为55.7%，生猪价格是非平稳序列；同理，母猪价格的t值是0.33，大于10%水平的ADF临界值-1.62，存在单位根的概率高达78.0%，因此母猪价格序列也是非平稳的。为获得平稳的时间序列，将变量取自然对数后进行一阶差分，而且由于本文主要研究超常波动下生猪价格与母猪价格的异向波动，将正常波动剔除，只留下超常波动区间内的数据，对其进行平稳性检验，检验结果见表5，变量dlnsz和dlnmz都是平稳的，因此可以通过互谱分析和Var模型进行实证分析。

2.2 互谱分析 对变量进行频谱分析时，可以将时间序列看做是不同频率的正弦波和余弦波的组合，通过傅里叶变换对不同的频率分量进行分解，从频域的角度对时间序列的周期特征进行分析。频谱分析有2类分析方法：单变量模型，通过谱密度函数分析单个变量的周期波动特征；多变量模型，可以利用互谱密度函数研究2个变量在不同的频率分量上的关系，其中通过相干谱和相位谱能得到变量间的相关程度以及时差关系。因此鉴于本文研究的是生猪价格与母猪价格之间的关系，选择互谱分析法。

互谱密度函数HXY（f）（f为频率）是不含有缺失值的平稳时间序列 ｛Xt｝和｛Yt｝ （t=0，±1，±2，...）互协方差函数RXY（k）的傅里叶变换：

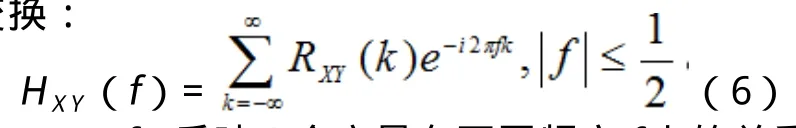
HXY（f）反映2个变量在不同频率f上的关系，但其本身值为复数，不方便进行描述，一般使用复数的极坐标表示形式，CXY（f） 和 QXY（f）分别表示HXY（f）的实部和虚部：

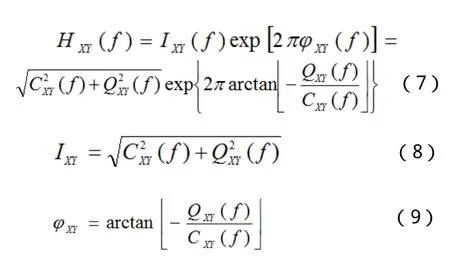
IXY（f）为互幅振谱，反映｛Xt｝和｛Yt｝在不同频率上振幅的相互关系，而一般在研究2个变量间的相关程度时，通常引入相干谱WXY（f） ，利用相干谱的平方进行衡量 ，相干谱是2个序列在各个频率f上振幅的标准化均值，公式如下：

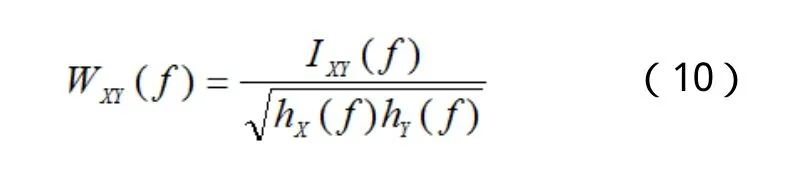
其中 HX（f） 和HY（f） 为｛Xt｝和｛Yt｝的谱密度函数，WXY（f）的取值范围在0～1，函数值越接近1，两者的相关度越高； φXY（f）为相位谱，用来测度1个序列领先或滞后于其他序列的各频率分量的长度，反映两者的相位差，若φXY（f）>0，表示序列｛Xt｝的相位大于｛Yt｝，｛Yt｝的波动落后于｛Xt｝φXY（f）个相位，反之同理，而具体的时差不仅与相位的大小、正负有关，还与周期长度（频率f的倒数）有关，

表4 超常波动与正常波动区间下的异向波动对比表

表5 变量定义及单位根检验

基于上述的互谱分析原理，对数据处理后的生猪价格和母猪价格进行互谱分析（｛Xt｝是对数差分处理后的母猪价格序列，｛Yt｝是对数差分处理后的生猪价格序列）。

如图2所示，对数差分处理后的生猪价格和母猪价格在0.023～0.054频率分量上谱密度较高，且在此区间内生猪价格在频率为0.023和0.046时达到峰值，说明生猪价格可能存在长度为21.67和43.33周的周期波动；而母猪价格在频率为0.023和0.054时达到极值，说明母猪价格可能存在长度为18.57和43.33周的周期波动。由此可见，2个变量存在2个较为明显的波动周期，周期长度为4～6个月和10个月，这与生猪的生物性周期大体一致，一般能繁母猪需要4个月左右的怀孕期，仔猪出生后需要1～2个月的哺乳保育期，之后经过4～5月的育肥方可出栏，从仔猪出生到出栏约6个月，而从能繁母猪怀孕到生猪出栏需10个月左右。因此半年前或10个月前的价格波动会对出栏量造成影响，进而影响生猪价格和母猪价格，形成新一轮波动。

图2 dlnsz（上）与dlnmz（下）的谱密度

表6 生猪价格与母猪价格的互谱分析结果（部分）

如表6所示，从相干谱平方来看，生猪价格和母猪价格相干谱的平方大多数大于0.5，而在周期长度大于15周时，相干谱的平方均在0.7以上，说明两者具有较强的相关性，并且在较长的波动周期中相关性更加明显；从相位谱来看，2个序列的相干谱数值较小，绝大多数的绝对值小于0.05，大于等于0.05的6个数值均为负数，从时差来看，领先滞后长度大于0.16周（1 d）的5个数值中，仅有1个是正值，这说明生猪价格领先于母猪价格，并且除在130周的周期分量上生猪价格领先母猪价格2周外，领先程度较小。

由前面单变量的谱密度函数得知，2个变量的主周期均在0.023～0.054频域内，即周期长度在18.57～43.33，在此范围内的相干谱平方均大于0.85，并在21.67周达到最大值0.96，相关性极强；在该频域内，2个变量的相位差在0左右波动，基本上不存在时差。由此可以得出，生猪价格与母猪价格具有相关性，并在主周期频域内密切相关；在波动时间为130周的周期中生猪价格变动先行于母猪价格2周，而在其他分量上基本同步。

表7 Var模型滞后长度检验结果

2.3 时间序列分析 互谱分析虽然可以确定2个变量间的相关程度以及在各频率上超前、滞后或者同步的关系，但不能确定变量间如何相关，而Var模型可以分析不同变量间的动态关系。因此，基于上述分析，构建生猪价格与母猪价格的Var模型，通过LR，FPE，AIC等标准确定滞后长度p，结果如表7所示，*表示从每一列标准中选择的最优滞后长度，由此确定该Var模型的p=1；通过AR根估计方法判断模型的稳定性，若Var模型所有根的倒数都在单位圆内（小于1），模型即是稳定的，反之则不稳定，检验结果显示其根的倒数分别为0.75和-0.08，均小于1，说明该模型是稳定的。

图3 母猪（生猪）价格对生猪价格上升的脉冲响应分析

由于构建的Var（1）模型是稳定的，可以通过脉冲响应函数，分析母猪价格与生猪价格之间的冲击响应，研究2个变量间的动态关系，得到数据处理后的母猪价格dlnmz对生猪价格dlnsz单位冲击的响应，本文建立的脉冲响应模型的滞后期数为30期，图3为母猪（生猪）价格对生猪价格上升的脉冲响应图。

如图3所示，当给生猪价格一个正向冲击，母猪价格在随后的第1周响应为正，在第2周达到最大后逐渐回落，最终趋近于0，这表明生猪价格与母猪价格正向相关，但由于响应在第2周达到峰值，说明存在2期的滞后，这与上一部分互谱分析的结果一致。虽然生猪价格发生波动后，响应期内的母猪价格与生猪价格同向变动，但不同的是，母猪价格对生猪价格响应值的斜率前2期为正，在第2周达到极值后斜率变为负数，且斜率随时间减速增加，最终趋近于0；而生猪价格对自身响应值的斜率一直为负，同时随时间减速趋近于0。也就是说，价格变化后前2期，母猪价格与生猪价格响应曲线的斜率正负不同，即响应值的变化趋势不同，这与本文第二部分所说的相对异向波动是一致的，因此可以确定，超常波动区间下确实存在生猪价格与母猪价格的异向波动。

3 结论及对策建议

3.1 结论 本文利用异步系数、互谱分析和时间序列分析，对生猪价格与母猪价格的波动以及两者之间的关系进行研究，识别并验证了两者间的异向波动，主要得出3点结论。

（1）超常波动区间下，生猪价格与母猪价格的波动密切相关。两波动间存在信号传递，生猪价格波动作为信号逆向传导，导致母猪价格发生波动，生猪价格波动略微领先于母猪价格波动；同时发现生猪价格和母猪价格存在4～6个月和10个月的主周期波动，与生猪的生物性周期保持一致。

（2）超常波动区间下，生猪价格与母猪价格间存在异向波动。生猪价格发生波动后，母猪价格同向波动，但波动趋势存在明显的异步性；同时超常波动区间下异步系数为0.66，稍高于正常波动区间的异步系数0.63，说明超常波动区间下的异步程度更强。

（3）异向波动可以看作是生猪价格超常波动的一个表征和警兆。异向波动对于超常波动的识别，预警和稳定具有重大意义，母猪作为生猪生产环节的上游，可以将其作为防控生猪价格超常波动的入手点，通过稳定母猪价格波动稳定生猪价格波动。3.2 对策建议 基于上述结论，本文以能繁母猪为入手点提出平缓生猪价格波动的一些对策建议。

（1）监控能繁母猪存栏数量，保障生猪市场供应能力。各省市对本地区能繁母猪进行统计，根据本地区生猪市场的供求情况，找到能繁母猪存栏量最低的警戒线；对能繁母猪存栏量50头以上的养殖户（场）进行备案，每隔一段时间统计1次实际数量，在母猪数量大幅度减少时，给予一定补贴，保证能繁母猪数量。

（2）对能繁母猪实行动态补贴制度。补贴时间的动态性：补贴如果每年都进行发放，养殖主体会将补贴纳入到正常的成本收益中，失去激励作用，因此对于生猪市场应该实时进行监控，在生猪市场持续低迷、疫病情况严重时，对能繁母猪进行补贴，激励养殖主体，保持生猪市场的活力；补贴金额的动态性：同时由于不同地区生猪市场受到的冲击程度不同，统一的补贴标准效果不理想，在国家统一补贴金额的基础上，各地区根据损失情况适当增加。

（3）根据生猪养殖利润，确定能繁母猪的补贴金额。在生猪养殖利润大幅度上时，由于育肥猪的回报期短、利润空间大，养殖主体受短期利益驱使，会减少猪舍中母猪存栏，增加育肥猪数量，从而导致新一轮价格上涨。通过对能繁母猪进行利润差额补贴，激励母猪养殖者，从而增加仔猪数量，进而增加市场上生猪的供应量，抑制生猪价格上涨。

[1] 毛学峰, 曾寅初. 基于时间序列分解的生猪价格周期识别[J]. 中国农村经济, 2008, (12): 4-13.

[2] 潘方卉, 刘丽丽, 庞金波. 中国生猪价格周期波动的特征与成因分析[J]. 农业现代化研究, 2016, (1): 79-86.

[3] 黎东升, 刘小乐. 我国生猪价格波动新特征——基于HP和BP滤波法的实证分析[J]. 农村经济, 2015, (6): 52-55.

[4] 何剑, 孙鲁云. 中国生猪市场的价格传导效应研究——基于仔猪与生猪价格的周数据分析[J]. 价格理论与实践,2016, (8): 105-108.

[5] 魏君英, 何蒲明, 马敬桂. 仔猪价格与生猪价格波动关系的实证研究[J]. 饲料工业, 2013, (21): 60-64.

[6] 何蒲明, 朱信凯. 玉米价格与生猪价格波动关系的实证研究[J]. 经济问题探索, 2011, (12): 87-90.

[7] Saengwong S, Jatuporn C, Roan S W. Modeling time series analysis between feedstuff and hog prices in taiwan[J]. J Agric Sci Technol A, 2011, (8): 1126-1129.

[8] 王利荣, 李明, 葛林霞, 等. 探索我国生猪价格波动与生产能力的关系[J]. 价格理论与实践, 2017, (3): 70-73.

[9] 岳冬冬, 王征兵. 一种测度数据序列协动性的同步系数法[J]. 统计与决策, 2011, (1): 4-6.

[10] 陈磊. 我国宏观经济指标周期波动相关性的互谱分析[J].统计研究, 2001, (9): 38-41.

[11] 李育峰, 李仲飞, 周潮. 银行信用风险与经济增长的关系及逆周期资本缓冲——基于向量自回归和互谱分析方法的研究[J]. 运筹与管理, 2016, (4): 150-156.

Recognition and Empirical Research on the Reverse Fluctuation between Hog Price and Sow Price

LI Hong-shu1, WANG Gang-yi1*, LU Feng-jun2, SI Run-xiang1

(1. College of Economics and Management, Northeast Agricultural University, Heilongjiang Harbin 150030, China;2. College of Economics and Management, China Agricuiyural University, Beijing 10083, China )

To study the relationship between pig price and sow price under the abnormal fluctuation range, and determine whether there is any reverse fluctuation, first, we recognit reverse fluctuation by asynchronous coefficien, and divid the sample interval into normal fluctuation and abnormal fluctuation according to amplitude; then we make empirical analysis through Cross-spectrum Analysis and Time Series Analysis. The study shows that the hog price is closely related to the sow price, and the fluctuation of the hog price is slightly ahead of sow prices fluctuation in the time; there is a reverse fluctuation between hog price and sow price under the abnormal fluctuation range, and the asynchronous coefficient is slightly higher than the normal fluctuation range; the reverse fluctuation can be seen as a representation and warning of abnormal fluctuations.

Hog price; Sow price; Reverse fluctuation; Cross-spectrum analysis; Time series analysis

F323.7

A

10.19556/j.0258-7033.2017-10-115

2017-05-10；

2017-07-26

国家自然科学基金（71303040）；教育部人文社科基金（13YJC790142）；中国博士后研究基金（2013M540268）；黑龙江省创新人才项目；东北农业大学青年才俊计划

李洪姝（1995-），女，山东平阴人，硕士研究生，主要从事畜牧经济研究，E-mail: 15754501306@163.com；司润祥（1990-），男，河南新乡人，硕士研究生，主要从事畜牧经济研究，E-mail: 827869250@qq.com

*通讯作者：王刚毅，E-mail：awgy@163.com