动态规划思想在ACM竞赛中的应用研究

刘雄辉　汪红宇　陈义明

摘要：动态规划算法是运筹学的一个分支，是求解多阶段决策最优的方法。该文介绍了使用动态规划算法的一定条件，并详写了使用动态规划算法解决决策性问题时的三大阶段和三大要素，以及动态规划算法与分治算法、贪心算法的关系。并以动态规划算法在ACM算法竞赛中的应用，来加强对于动态规划的理解。

关键词：动态规划；最优；算法；策略

中图分类号：TP311 文献标识码：A 文章编号：1009-3044（2017）18-0238-02

动态规划算法是求解多阶段决策最优的方法，它与分治算法和贪婪算法有一定的相似度，它能够高效地处理分治和贪婪不可以处理的问题。

1使用动态规划算法的条件

动态规划算法从问世到现在，在很多方面得到了广泛运用。如最短路线、背包问题、最小生成树等问题，动态规划算法比用其他算法求解更加便利。然而动态规划并不适用于所有的问题，只有满足以下条件才能使用动态规划求解：

1）最优化原理

2）无后效性

最优化原理是动态规划的基础，假使一个问题没有最优化原理的支持，就不能使用动态规划算法求解。那么最优化原理是什么呢？简单来说就是一个最优策略的子策略，对于它的初态和终态而言也必是最优的。

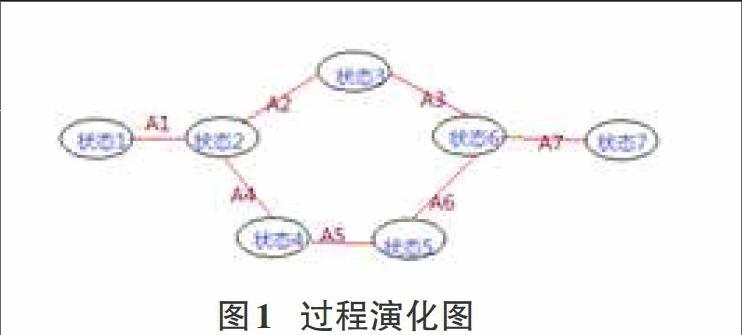
例如图1，状态1→状态7的最优策略为A1-A2-A3-A6-A7，那么其子策略A2-A3也一定是状态2→状态6的最优策略。

无后效性是问题可使用动态规划算法的一个标记。我们可以理解为：一个阶段的状态只要确定了，那么后面过程的演化不会受前面状态和策略影响，以图1举例说明：状态3和状态4只能够由状态2经过决策A2、A4得来，和其他的状态没有任何的关系。

2动态规划问题求解模式

动态规划是一种以多阶段决策问题的特点为依据，将其转变成一系列相互联系的单阶段问题，再逐个解决的说法。一些静态的问题，只要我们找到可以将其划分成相互联系“阶段”的特征，就可以转化为多阶段动态问题。

动态规划所处理的问题是一个多阶段的决策问题，以图1为例，它由状态1开始，在中间经过不同的决策选择，达到状态7。这些决策形成了一个最优策略序列（A1-A2-A3-A7），同时确定了整个过程的一条活动路线（状态1→状态2→状态3→状态6→状态7）。

动态规划算法设计拥有必定的形式，一般必须经过三个步骤：

1）划分阶段：按照我们找到的特征，将其划分成相互的阶段。

2）确定每一个阶段的状态和状态变量。

3）确定状态转移方程：根据前后阶段的演变规律写出状态转移方程。

求解动态规划问题时，我们需要确定它的三大要素：

1）问题每一个阶段

2）每一个阶段对应的所有状态

3）从前一个阶段转化到后一个阶段之间的递推关系

只要我们确定动态规划的三大要素，整个求解过程就能够使用最优决策表来表示，最优决策表是一个多维的表（在ACM算法竞赛中最常见的是二维），决策的阶段和状态对应表的行与列，表中数据为对应阶段和状态下的最优值，从初始状态开始，以某一优先顺序填写表格，填写完之后根据表中数据得到最优解。

3动态规划算法与其他相近算法的关系

动态规划算法和贪婪算法都是由局部最优推导全局最优的一种递推算法。贪婪算法与动态规划算法的主要区别是贪心选择性质，它是问题可以使用贪婪算法的前提。

贪婪算法做出的选择只是在当前情况下最好的，而不会从整体最优上考虑，它的选择仅仅是局部最优。贪心选择性质就是：可以通过贪婪算法的得到的局部最优得到整体最优解。而在动态规划算法中，中间阶段的最好选择，不能保证最后的结果是最优的。

动态规划与分治法都是通过组合子问题的解求解原问题的算法。不同的是，分治算法把原问题分为没有联系的子问题，递归地求解子问题，然后把子问题的解组合，以求解原问题。而动态规划对应子问题重复的情况，即不一样的子问题具有公共的子子问题（子子问题是将子问题再次划分得到的子问题）。面对这样的问题，分治算法将完成许多不必要的任务，它会反复地求解那些公共的子子问题。而动态规划对于重复的子子问题只求解一次，并把它记录在最优决策表中，从而避免了重复子问题的计算工作。

在分治法示意图中，我们可以知道已知f（n）f（n-2）+f（n-4），求f（10）。f（2）、f（4）都是重复子问题，使用动态规划的话，我们就可以直接记录值，以避免重复的求解，所以动态规划算法实际上是在以空间换时间。

4动态规划算法在ACM竞赛中的应用

为了能够更好地了解动态规划算法的使用，以下面的题目来介绍一下动态规划算法在ACM算法竞赛中的应用，加深对动态规划算法的理解。

Problem Description

子序列是一个序列通过删除若干元素后可以得到的序列。公共子序列就是一个序列同时是多个序列的子序列。题目给出两个序列X和Y，求解XY的最长公共子序列长度。

Input：输入若干组数据，每组数据包括：序列X和Y，中间使用空格分开

Output：对应每组数据输出序列X和Y的最长公共子序列长度

输入：ABCABCDEA BCBCEA输出：6

问题分析：

题目已知了序列X和序列Y，要求求解其最长公共子序列的长度。对于一个长度为n的系列，我们考虑其中元素的去与留，会有2*种可能。所以序列XY的长度較短的话，我们可以使用遍历。当n很大的时候，使用遍历将使程序的时间复杂度很高，明显不可取。

所以我们使用动态规划算法来解决这道问题，采用二维数组来标识中间计算结果，避免重复的计算来提高效率。我们以在字符串X、Y的不同位置划分阶段，用num[i][j]二维数组保存每一个阶段下的状态（即字符串X前面i个字符和字符串Y前面i个字符的最长公共子序列长度）。根据只有当序列中X[i]==Y[j]序列X[1…i]Y[1…j]的最长公共子序列长度比序列X[1…i-1]Y[1…j-1]的最长公共子序列长度大1。由此可以得到最长公共子序列长度的状态转移方程（图3）。再根据状态转移方程，我们可以依次填写最优决策表（图4）。其中字符串X对应的是二维数组nun的行，字符串Y对应的是二维数组nun的列。

5结束语

动态规划算法是求解决策过程最优化的数学方法，自问世以来，在诸多方面得到了广泛应用。而在ACM程序设计大赛中，动态规划算法也是一位从不缺席的常客。但是要很好地利用动态规划算法，就要充分的理解动态规划问题的求解，区分动态规划和其他算法的不同。相信在将来，动态规划将在更多的领域得到更好的应用与发展。endprint