不同空间权重定义下中国人口分布空间自相关特征分析
2017-10-21吴珣,杨婕,张红
吴 珣,杨 婕,张 红
(西南交通大学 地球科学与环境工程学院,四川 成都 611756)
0 引 言
人口分布是指人口数量规模的地域分布,它是人口地理学研究的关键,与人口数量、空间分布和一定区域内人口密度紧密相关[1]。研究人口分布状况、揭示人口分布与空间位置的关系,对于增进人地关系的理解,实现人口、资源、环境可持续发展有着十分重要的作用[2-4]。
中国人口众多,地域辽阔、自然环境多样,人口分布面临的主要问题有:大城市病、高密度连绵城市群的环境污染、大片乡村缺少就近特大城市辐射带动的发展难题、生态气候等自然条件恶劣地区人口的生存困境、以及高密度大流量的人口迁移等[5-6]。自1935年胡焕庸提出了“瑷珲-腾冲”线至今[7],“胡焕庸线”一直是体现中国人口空间分布地域差异的一条最基本的分界线。当今中国人口正处于转折点上[4],李克强总理在国家博物馆参观人居科学研究展时,向社会和科学界提出“胡焕庸线怎么破”的命题,为中国人口分布研究带来新的机遇与挑战[8]。
由于人口分布受自然与社会双重影响,对人口的研究涉及社会学、经济学、地理学、人口学、环境科学等多个学科,研究角度诸如聚落、人口流动与迁移、居民点分布、人口与产业格局、区域发展关联分析等[5,9-10]。由于空间相互联系和相互作用是揭示事物与现象空间分布特征和动态变化规律的基础[11],空间自相关性也成为研究人口分布格局及变动的最为有效的工具之一[12]。当前人口自相关研究多集中于人口自相关模式、人口自相关与社会经济关联分析等[13-14],对于人口自相关分析中空间权重矩阵建立的方法及其比较的研究较少。此外,作为快速交通流线的主要形式,高速铁路建设可提高可达性,有效拓展区域人口流动空间,并引导人口和产业的集聚趋势[15]。有必要根据高铁可达性重新定义空间权重矩阵,揭示高铁影响下的人口空间自相关特征。
综上,本文基于距离阈值和邻接关系定义多种空间权重矩阵,建立高铁两小时经济圈空间权重矩阵,使用Moran's I指数,刻画中国人口分布的空间自相关特征,并比较不同空间权重矩阵下的中国人口空间分布自相关特征的一致性与差异性。
1 空间自相关与空间权重矩阵
1.1 空间自相关:定义与计算方法
空间自相关是地统计的基础。1973年,Cliff和Ord出版了《空间自相关》一书,为度量地理空间单元间的相互联系提供有效的统计分析手段[16]。随后,Tobler指出了空间自相关的普遍性并提出了地理学第一定律,即地表所有事物和现象在空间上都是关联的,且距离较近的事物比距离较远的事物联系更紧密[17]。当前空间自相关分析已成为刻画空间关联模式、研究空间分异和空间格局的有效方法。相较洛伦斯曲线、基尼系数等传统度量指标而言,运用空间自相关分析可以较好地表达人口分布的集聚现象,揭示人口格局的空间结构和空间相互作用。
目前,刻画空间自相关指数的统计量主要有Moran's I和Geary's C指数。由于Moran's I是最早提出的、简单且最常用的统计量,并且研究发现在判断一个区域是否存在空间聚集,尤其是估计聚集区域位于区域的边缘时,Moran's I指数比Geary's C统计的结果更为可靠[18],故本文选取Moran's I指数作为分析指标。
空间自相关分为全局空间自相关和局部空间自相关。其中,全局空间自相关主要用于描述某区域内某种现象的整体空间分布情况,以判断该现象在空间上是否存在聚集性[12]。全局空间自相关指数Moran's I 的计算公式为:

式中,xi和xj为位置i和位置j的特定属性,x-为其相应的均值,wij为空间权重矩阵,代表i和j的空间关系。空间权重矩阵可以量化数据集要素中存在的空间和时态关系。虽然空间权重矩阵文件可能具有多种不同的物理格式,但从概念上讲,可以将空间权重矩阵看作一个表格,数据集中的每个要素都对应着表格中的一行和一列。任意给定行/列组合的像元值即为权重,从而量化这些行要素和列要素之间的空间关系,通常通过距离或邻接关系来定义权重,下一节将详细介绍各类权重设置方法。其中S定义为:
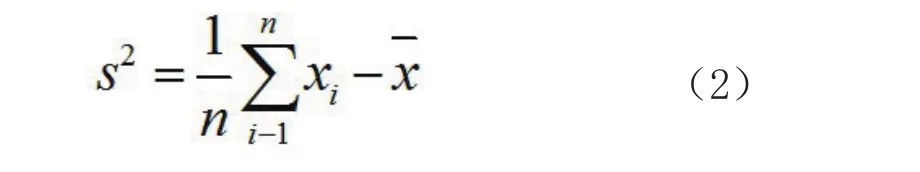
Moran's I 的取值范围为[-1,1]。当Moran's I指数值接近0,指示随机趋势或不相关;当Moran's I为正时,指示聚集趋势,即距离邻近的事物性质越相似。当Moran's I为负时,指标离散趋势,即距离邻近的事物间的差异越大。计算出Moran's I后,一般要对其进行显著性Z检验,计算公式为:

式中,E(I)和Var(I)分别表示Moran's I指数的期望和方差。
局部空间自相关分析侧重于研究局部范围内空间对象属性值在的空间相关性,局部Moran's I指数的计算公式如下:

其中Zi=(xi-x-)/S,S与公式(1)中一致;Zi,Zj分别为空间单元i与j某个属性的标准值,反映属性值与均值的偏差程度。I值的具体含义与全局空间自相关指标类似。
全局空间自相关和局部空间自相关从整体和局部探测空间对象的分布情况,关键在于空间关系的定义,都需要考虑空间权重矩阵。不同的空间权重对应着不同的空间关系,从而给空间对象的全局和局部空间自相关分析带来差异。本文将人口分布作为研究对象,运用全局和局部自相关分析方法,同时皆考虑不同的空间权重矩阵,从全局和局部揭示不同邻近关系下人口空间分布格局和空间相互作用。
1.2 空间权重矩阵
如前所述,与传统统计学相比,全局与局部Moran's I指数均考虑了空间权重。空间权重矩阵是空间相邻关系的主要表达方式,刻画了空间对象间的相互邻接关系。当前有多种空间权重定义方式,如基于距离的权重矩阵、Queen权重矩阵、Rook权重矩阵、K最近点权重矩阵、Delaunay权重矩阵等。下面介绍几种常见权重矩阵与本文给出的权重矩阵定义:
1)基于固定距离的空间权重矩阵
在空间数据中,距离是空间对象的直线距离或球面距离。在小的地区(小尺度的研究),可以忽略地球的曲率,距离的计算可以采用欧氏距离或曼哈顿距离。在较大的区域(大尺度研究),距离的计算要考虑地球的曲率。FIXED_DISTANCE(以下简称FD):首先需要建立一个距离阀值d,比较空间目标两点之间的距离dij与阈值d的关系,小于阈值取1,其他取0。此方法中,距离代表着空间关联性,有效刻画人口空间意义上的关联性,不过阈值距离选择与实际的应用相关。权重矩阵的定义如下:

2)基于K-最近邻权重
K_NEAREST_NEIGHBORS(以下简称KNN):此方法的计算需预先设定K值,并分别计算空间目标的两两之间的距离dij在观测点周围随机选择与其最近的k个点,认为是相邻的,权重为1,其余为0。此方法中,空间对象相邻关系的构建随机性较强,缺乏客观性。权重矩阵的定义如下:

3)基于邻接关系权重矩阵
根据直接相邻关系,将空间目标的位置邻接关系定义为下列两种情形中的任何一种:ROOK CONTIGUITY(以下简称RC)、QUEEN CONTIGUITY(以下简称QC)。对于Queen权重矩阵,只要两个空间对象之间有公共的边或同一点,就认为两者是相邻的,权值为1,否则权值为0。对于Rook权重矩阵,只要两个对象之间有公共边,就认为两者相邻,权值为1,否则为0。在邻接关系中,还存在高阶和低阶效应。就省域为例,一个省的二阶邻近,代表与该省域邻近省域的邻近省域也与该省相邻。此方法中,注重区域间边界关系,受客观边界影响较强。一阶邻近Rook权重矩阵的定义如下:

4)基于通行时间权重矩阵
我国高速铁路网的不断完善,不仅可以促进经济的流通,对人口的分布也会有一定的影响。根据通行时间(高铁两小经济圈),给出省与省之间通行时间的权重矩阵(以下简称HSR2)。在一定条件内(两小时内)高铁可以到达的权值为1,否则为0。本文方法,通过高铁可达性重新定义空间权重矩阵,揭示高铁影响下的人口空间自相关特征。权重矩阵的定义如下:

不同空间权重矩阵关注空间单元的不同方面,如Queen权重矩阵侧重于空间单元间的直接相连性,而阈值权重矩阵则关心空间单元间距离的阻隔作用。本文构建了两种阈值权重矩阵,一种为几何距离阈值(FD),其值设为500 km,其依据2015年3月实施高铁新建设计开行速度250 km/h,2小时大致能行驶的距离约500 km[19];另一种为根据通行时间(高铁两小时经济圈,HSR2)定义的阈值权重矩阵,利用两种阈值权重矩阵从空间和时间两个维度进行人口分布空间自相关对比分析。此外,还考虑了Rook、Queen两种不同邻接关系定义,阶数分别为一阶(RC1,QC1)和二阶(RC2,QC2),既充分考虑省域间边界邻接关系,同时探测高阶邻接带来的影响;K最近邻点权重矩阵考虑了三邻域(KNN3)和六邻域(KNN6),虽然存在一定的随机性,但不失为空间邻近关系的一个补充,三个或六个邻域也与实际情况较为接近。
2 中国人口空间分布自相关特征分析
本文以省及直辖市作为基本分析单元,人口数据由《中国人口年鉴(2010年)》得到。
2.1 中国人口分布的一般特征
以省及直辖市作为基本分析单元,得到图1所示的中国省级人口密度空间分布图。空间分布上,人口密度高等级省份主要分布于中国东部沿海,中部平原,人口数量巨大,并且沿海各行政区域面积较小,经济条件较好,人口密度相对较大。低等级人口密度省份主要分布于西北和西南地区,以盆地、高原和丘陵地带为主,经济欠发达,地广人稀,人口密度普遍不高。整体呈现东部高于西部的空间特征。中国人口密度分布的东南和西北分异突变线,与“胡焕庸线”大致吻合。

图1 中国省级人口密度分布图Fig. 1 Distribution density map of provincial population in China
2.2 不同空间权重定义下的中国人口分布全局自相关特征分析
使用Geoda软件进行全局空间自相关性分析,得到中国省级人口密度分布全局Moran'I值(见表1),为了便于分析比较,图1为相应的Moran'I和统计量Z数值分布散点图。
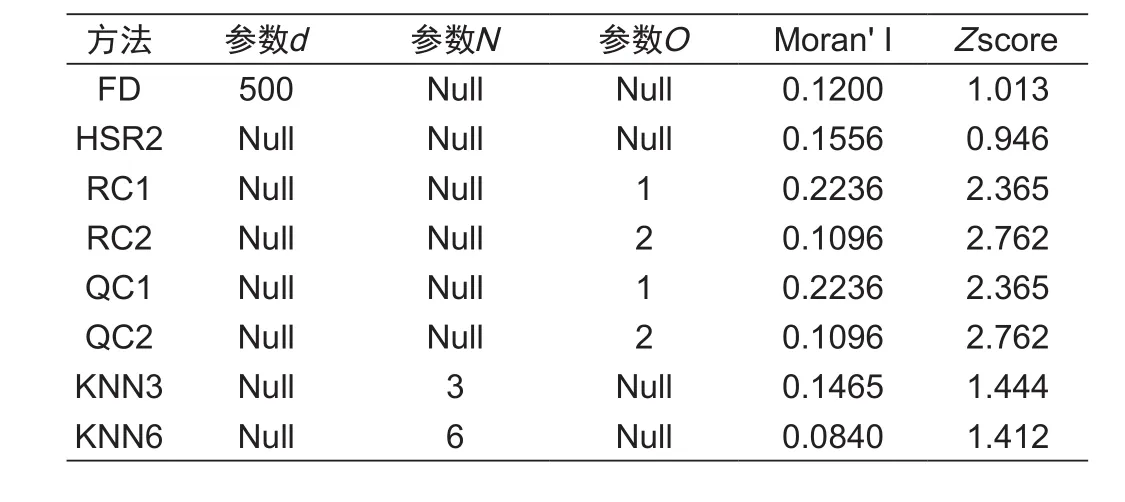
表1 不同邻近关系下全局Moran's I值及其检验统计量Z值(α=0.05)Tab.1 Global Moran's I and Z score in different proximity relations

图2 不同邻近关系下全局Moran's I值及其检验统计量Z值(α=0.05)Fig. 2 Global Moran's I and Z score in different proximity relations
结合表1和图2,①从Moran's I值大小来看,四类不同的空间邻近位置关系所得到的全局Moran's I指数值均大于0,2010中国省域人口密度分布正的空间自相关性保持一致;②不同空间邻近关系,在保持空间正相关的空间模式下,其显著性水平有高有低。检验统计量Z值在5%的显著水平下,RC、QC方法Z值均大于1.96,显著性水平较强,KNN方法Z值接近1.96,显著性水平次之,FD和HSR2方法显著性水平最弱;③对于RC、QC方法,随着阶数O增加,Moran's I值下降很快,KNN方法随着邻接数增加,也表现相似的现象。揭示高阶效应存在于人口密度的空间自相关分析中,也即是省域之间一阶邻近对人口密度空间自相关分析影响较大,各个省份人口密度和邻近省份人口密度关系紧密相关。
全局空间自相关指数概括了在一个总的空间模式中空间依赖的程度,揭示了全局综合特征,但是还不能表明各个省域与周边邻近省域之间的局部空间关系,因此以下利用局部自相关的分析方法来揭示我国各个省份人口密度的空间依赖关系。
2.3 不同空间权重定义下的中国人口分布局部自相关特征分析
图3展示了八种空间权重矩阵下人口密度分布局部Moran's I指标图。图例中,白色代表没有显著性,也即是没有空间关联关系;正相关有两种类型,红色代表人口密度高于均值省份被人口密度高于均值的省份所包围(HH),绿色代表人口密度低于均值的省份被人口密度低于均值的省份所包围(LL);而负相关也有两种类型:人口密度高于均值的空间单元被人口密度低于均值的邻域所包围(“高—低”关联或HL,用粉色表示),或者相反(“低—高”关联或LH,用紫色表示);灰色代表其他。
结合图3与表2,FD和HSR2方法得到的局部空间自相关结果表明:局部空间自相关类型中,无邻域省份和非显著性省份占主要,FD方法含有4个HH型和一个LH型,HSR2只含有2个HH型,所占比例都较小;空间分布上,以小型“组团”形式出现,聚集性较弱,HH型主要分布在江浙一带,安徽为LH型;实际中,江浙沿海一带,人口密度较大,空间距离与发达的高铁系统对其人口密度制约度较低,影响较小。
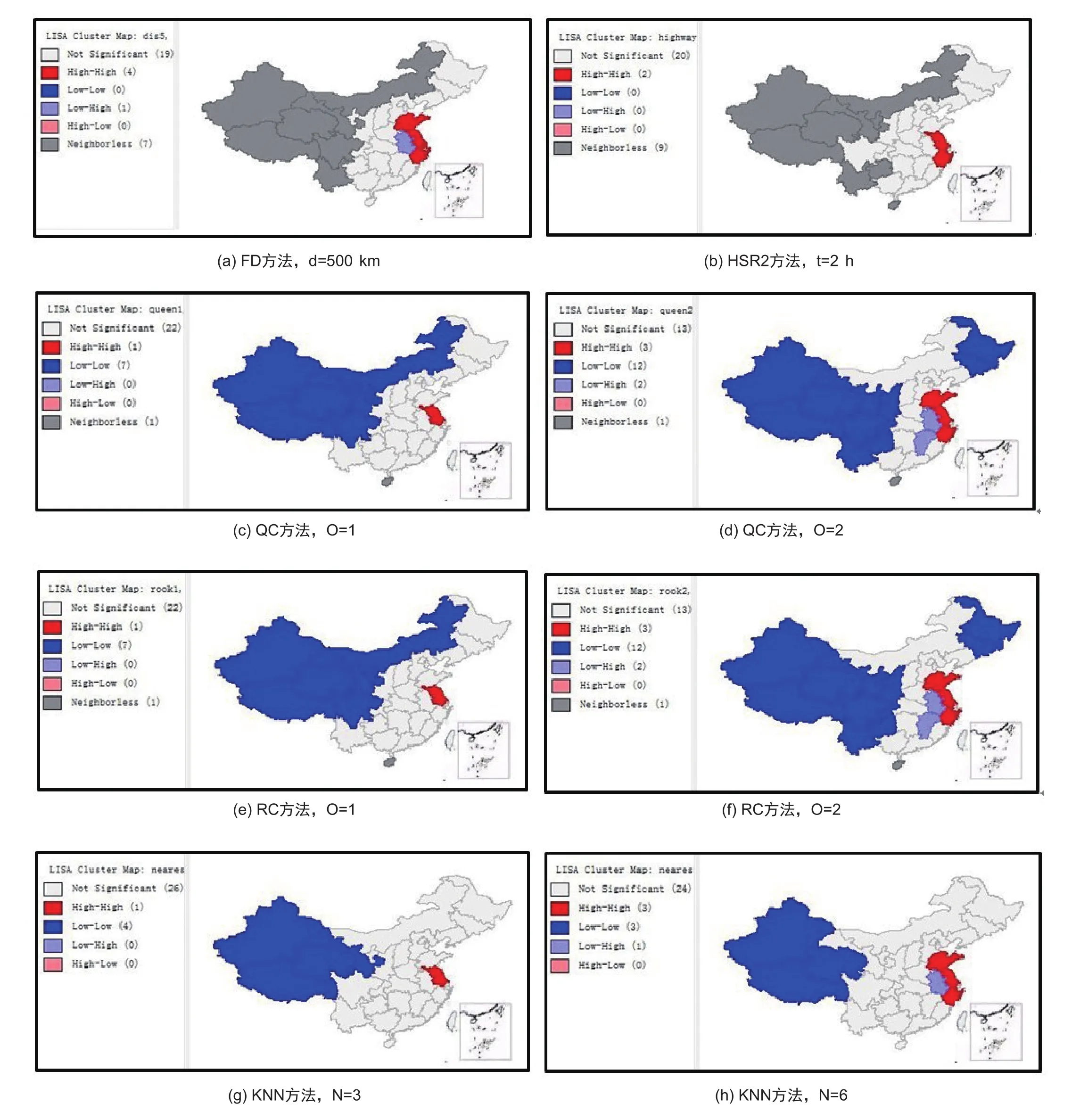
图3 2010年中国各省域人口密度局部空间关联模式图Fig. 3 Local spatial association of provincial population density in China

表2 不同权重矩阵对局部空间自相关的影响Tab.2 Effects of spatial weight matrices on local Moran's I
对于QC方法和QR方法,绝大部分省份的空间自相关性并不明显,且阶数一致时,局部自相关类型保持一致。当阶数O为1时,含有1个HH型,7个LL型。空间分布上,LL型主要集中在胡焕庸线的西北地区,HH型为江苏;当阶数O为2时,HH型有3个,LL型有13个,LH型有2个,高阶效应带来的影响在其产生作用。空间分布上,内蒙古不再是LL型,其次LL型中增加了黑龙江和吉林两省,并且HH型主要集中在江浙沪一带,LH型也出现在安徽江西这样人口密度不大的省份。实际中,HH型依然出现在江浙一带,其人口密度大,经济较为发达,LL型中增加西南地区,云贵川地区人口密度相对较小,经济相对落后,人口密度呈现出LL型的抱团模式。
至于KNN方法,非显著性省份占主要部分,三邻域和六邻域自相关结果也有一定差异。三邻域KNN方法,含有1个HH型,4个LL型,所占比例较小。空间分布上,LL型主要集中在西北地区,HH型为江苏;六邻域KNN方法,含有3个HH型,3个LL型,1个LH型,空间分布上,LL型依然集中在西北地区,HH型集中在江浙沪地区。
由此分析可知,不同的空间权重矩阵下,在局部自相关性上表现为一定的差异,但总体上各个省域人口密度对邻近省域人口密度影响一般都较为显著。中国西部各个省份和西南一些省份保持着LL型的关联模式,HH型的关联模式一般都集中在东部和中部;基于距离的空间权重矩阵与基于邻接关系的空间权重矩阵表现出的空间关联模式,其差异性较大,LL型的关联模式并不是很多。
由于受地形和气候环境的影响,加上东部沿海地区改革开放的程度较高,客观上造成东西部的经济发展不平衡,使得西部发展较慢,人口密度一直偏低,东部人口密度较高。在“胡焕庸线”西北地区,人口密度保持着LL型的空间关联模式占主导,RC方法和QC方法探测的结果较为明显,一致表现为西部地区人口密度小的省份,其周边省份人口密度也较小。八种空间权重矩阵并没有检测出HL型的空间关联模式,说明人口密度大的省份,其周边人口密度并不会很小,不过几乎每种空间权重矩阵都检测出了江苏省HH型的空间关联模式。
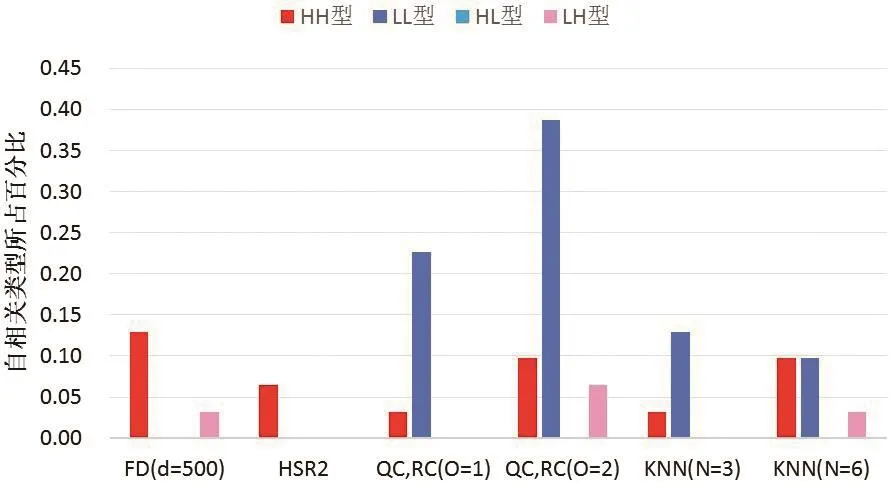
图4 不同权重矩阵对局部空间自相关的影响Fig. 4 Effects of spatial weight matrices on local Moran's I
3 结束语
中国多样化的自然环境造就人口分布区域间差异,人口分布的研究对实现人口、环境、资源可持续管理具有深刻意义。相对于洛伦斯曲线、基尼系数等传统度量指标,运用空间自相关分析可以较好地表达人口分布的集聚现象,揭示人口格局的空间结构和空间相互作用。然而当前测度人口空间自相关特征多采用单一邻近关系构造空间权重矩阵,忽视了不同空间邻近关系对自相关特征分析结果的影响。
为了弥补当前人口相关性分析采用的空间权重矩阵过于单一的不足,本文对比分析不同空间权重矩阵下,中国人口空间自相关分布特征,研究结果表明:①在不同空间邻近关系下,中国省域人口密度分布在全局自相关上均呈现空间正自相关,但其显著性水平有高有低;②局部自相关分析结果在空间分布上,以小型“组团”形式出现,因中国特定的地形和悠久的历史文化,使得Moran's I指数表现出较大的差异性和偶然性。③自定义的空间权重矩阵结果验证了其他结构的高—高相关。
本文采用的空间结构并不一定包含了所有的空间结构,同时所采用的数据是2010年中国各省份人口,是静态的,而对于多时间段的人口密度的分布和交通的飞速发展以及快速城镇化带来的人口剧烈流动对“胡焕庸”线的稳定性有待进一步研究。
