小兴安岭阔叶次生林典型树种单木生长模型的建立

吴 瑶,张怡春,秦凯伦，廉 毅

(1.黑龙江省林业科学研究所，黑龙江 哈尔滨 150081；2.东北林业大学，黑龙江 哈尔滨 150040；3.白河林业局，吉林 延边 133613)

小兴安岭阔叶次生林典型树种单木生长模型的建立

吴 瑶1,张怡春1,秦凯伦2，廉 毅3

(1.黑龙江省林业科学研究所，黑龙江 哈尔滨 150081；2.东北林业大学，黑龙江 哈尔滨 150040；3.白河林业局，吉林 延边 133613)

以小兴安岭过伐林区阔叶次生林典型类型(杨桦林、硬阔林)为研究对象，通过建立阔叶次生林典型类型(柞树、白桦、黑桦)的单木生长模型，对小兴安岭过伐林区阔叶次生林主要树种的生长进行预测，直接判定各单木树种的生长状况。研究结果表明，林木直径是影响阔叶次生林主要树种单木生长量的最主要因素，直径越大，定期直径生长量也越大；林木直径是影响林木枯损的主要因子，林木直径越大，枯损概率越小。

阔叶次生林；单木生长模型；单木枯损模型；林分密度；小兴安岭

单木模型是以固定标准地或森林资源清查固定样地的林木生长和枯损资料为依据，模拟林木的生长和枯损过程，与全林分模型或径阶模型不同，单木生长模型生长模拟的核心是林木个体在林分中的竞争位置,即竞争指数，以竞争指数为自变量，以林木的生长(胸径的生长)为因变量，便可建立单木的竞争模型。本研究是以小兴安岭过伐林区阔叶次生林典型类型(杨桦林、硬阔林)为研究对象，通过建立阔叶次生林典型类型(柞树、白桦、黑桦)的单木生长模型，对小兴安岭过伐林区阔叶次生林主要树种的生长进行预测，直接判定各单木树种的生长状况，对于指导森林分类经营具有特殊意义。

1 研究区域概况

小兴安岭位于中国黑龙江省东北部，西与大兴安岭对峙，位于北纬46°28′～49°21′，东经127°42′～130°14′。小兴安岭山脉西北接大兴安岭支脉伊勒呼里山，东南到松花江畔张广才岭北端，黑龙江与松花江的分水岭。林业施业区划面积为386万 hm2。 小兴安岭属低山丘陵，地理特征是“八山半水半草一分田”。北部多台地、宽谷；中部低山丘陵，山势和缓；南部属低山，山势较陡。最高峰为平顶山，海拔1 429 m。西部铁力市位于松嫩平原，地势呈波状。

2 数据的收集与整理

本研究在小兴安岭黑河地区的逊克县和爱辉区，收集阔叶次生林优势树种数据2 622株，包括白桦、黑桦、山杨、椴树、柞树等，根据研究的需要，选择了最具代表性的柞树、白桦、黑桦作为阔叶次生林典型树种单木生长模型的研究对象，同时收集解析木数据200株，作为单木生长模型的研究对象。计算各优势树种的平均胸径、平均树高、平均断面积，将计算结果建立数据库，用于建立单木模型的数据准备工作。

3 研究方法

3.1 地位级指数

运用SPSS 16.0软件，将整理后的各样地优势树种的平均高和平均年龄数据进行拟合，选择剩余标准差(Sy，x)、剩余均方(MSE)和相关指数(R2)作为拟合优度，分别带入Logistic方程、Chapman-iChards方程、Schumacher方程和Korf方程进行分析，最终选择Schumacher方程为最优模型，作为优势树种的地位级指数导向曲线：

HT=Aexp(-k/t)

(1)

式中：HT为林分平均高，t为林分年龄，A、k为待定参数。

各优势树种地位级指数导向曲线参数预估结果和模型统计量见表2。

由各主要树种的平均高生长曲线和基准年龄(tI),可以算出各样地的地位级指数(SCI):

SCT=HTexp[-k(1/t1-1/t)]

(2)

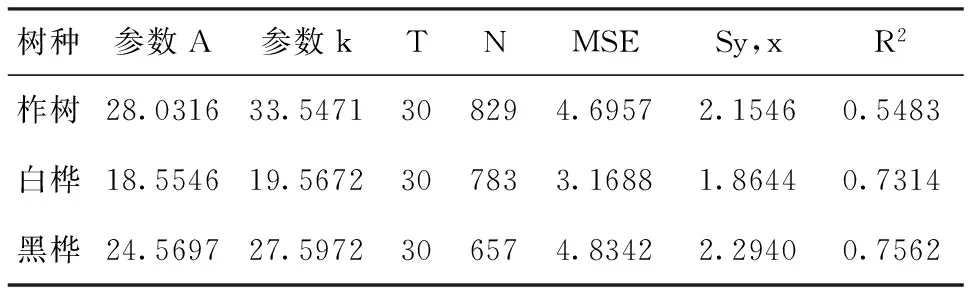
表2 地位级指数导向曲线拟合结果

3.2 林分密度

最大密度时，各优势树种每公顷株数(N)与林分平均直径(Dg)之间的经验方程如下：

(3)

式中:N为单位面积株数；Dg为林分平均胸径；a为大密度线的截距；p为最大密度线的斜率。

对(3)式两边取对数可得：

lnN=lnα-βlnDg

(4)

各优势树种最大密度方程拟合结果见表3。

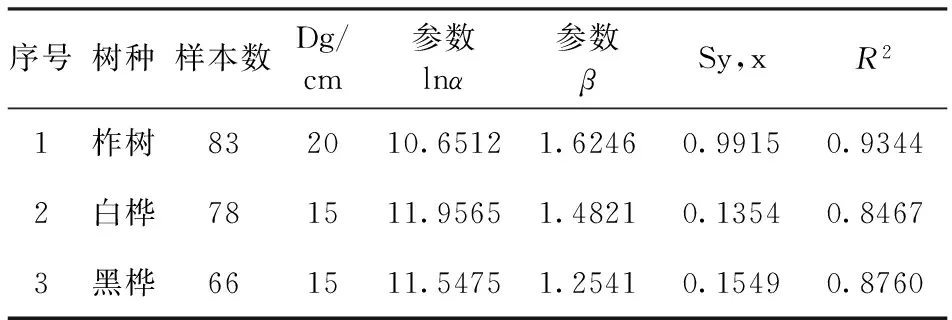
表3 最大密度方程拟合结果

林分密度指数(SDI)：

SDI=N×(D0/Dg)-β

(5)

式中：N为单位面积株数；Dg为林分平均胸径；D0为基准直径。

3.3 单木生长模型的建立

建立与距离无关的单木生长模型不需要树木的空间信息，公式(6)为表达树木大小、竞争和立地变量的函数

ln(DGI)=a+b×SIZE+c×COMP+s×SITE

(6)

式中：DGI为定期林木平方直径生长量(带皮)；a为截距；b为大小变量的向量系数；c为竞争变量的向量系数；s为地位变量的向量系数；SIZE为林木大小因子；COMP为竞争因子；SITE为立地因子。

采用胸径来表达林木大小因子函数：

b×SIZE=b1ln(D)+b2×D2

(7)

式中：D为胸高直径。

为建立与距离无关的单木模型,选择比对象木的直径大的树木的断面积之和(m2·hm-2)、林分密度指数、林分每公顷断面积、对象木与林分平均直径之比、对象木直径与林分中最大林木直径之比和郁闭度作为竞争指标建立竞争函数。

竞争函数表达式为：

c×COMP=c1×BAL+c2×SDI+c3×G+c4×RD+c5×P+c6×DDM

(8)

式中：BAL为比对象木的直径大的树木的断面积之和(m2·hm-2)；SDI为林分密度指数；G为林分每公顷断面积；RD为对象木与林分平均直径之比；DDM为对象木直径与林分中最大林木直径之比；P为郁闭度。

选择立地级指数、坡度、坡向、坡位、海拔、土壤等立地因子建立立地条件函数，公式为：

s×SITE=d1×SCI+d2×SL+d3×SL2+d4×SLS+d5×SLC+d6×SD+d7×ELV

(9)

式中：di为待定参数(i=1-4)；SCI为立地级指数；SL为坡率值，即坡度的正切值；SLP为坡向；

SLS和SLC为坡率和坡向SLP的组合项，SLS=SLsin(SLP),SLC=SLcos(SLP)；SD为土壤厚度；ELV为海拔。

整理后得到竞争指标和立地条件的关系式为：

ln(DGI)=a+b×SIZE+c×COMP+s×SITE=a+b1ln(D)+b2×D2+c1×BAL+c2×SDI+c3×G+c4×RD+c5×P+c6×DDM+d1×SCI+d2×SL+d3×SL2+d4×SLS+d5×SLC+d6×SD+d7×ELV

(10)

3.4 单木枯损模型

采用Lgisitc方程构建单木枯损模型,表达式为：

Pi=1/[1+exp(-y)]

(11)

式中：Pi为一定时期内第i株树的枯损概率；y=a0+a1x1+a2x2+……+anxn；x1□xn为预测变量。

本研究在考虑胸径和生长量的同时，还要考虑林分因子，因此选择胸径(DBH)，胸径生长量(DGR)，公顷断面G，郁闭度P郁,相对直径RD作为预测变量，单木枯损模型表达式为：

P=1/(1+exp(a0+a1DBH+a2DGR+a3G+a4P郁+a5RD))

(12)

式中：P为单木定期枯损概率；DBH为初期直径；DGR为定期胸径生长量；G为公顷断面积；P郁为郁闭度；RD为相对直径。

4 结果与分析

4.1 单木生长模型

对柞树的模型拟合过程如表4所示，最多可以引入9个变量，调整复相关系数为0.62。模型拟合结果见表5。

表4 柞树单木生长模型拟合过程

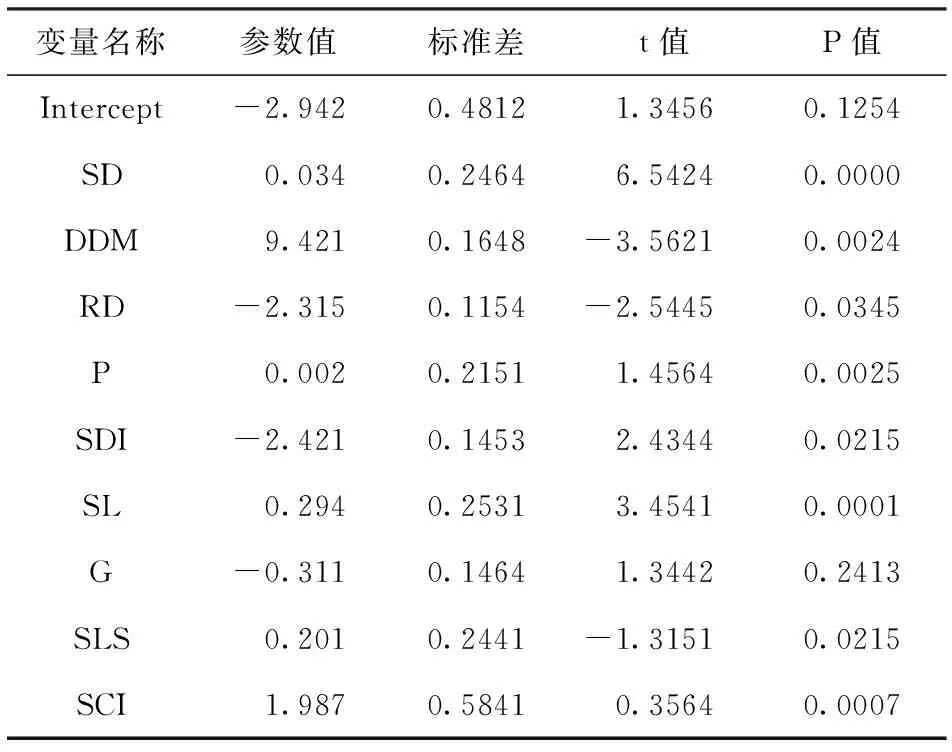
表5 柞树单木生长模型拟合结果

模型表达式为：

ln(dg)=-2.942+0.034×SD+9.421×DDM-2.314×RD+0.002×P-2.421×SDI+0.294×SL-0.33×G+0.201×SLS+1.987×SCI

(13)

可见，最终引入柞树单木生长模型的自变量包括竞争因子中的对象木直径与林分中最大林木直径之比、对象木与林分平均直径之比、林分密度指数、公顷断面积和郁闭度，立地因子中的土壤厚度、坡率值、SSL和SCI,说明竞争因子和立地因子对柞树影响较为明显。

图1为柞树生长模型的残差直方图，可以看出，残差服从近似正态分布，说明模型的拟合效果比较好。

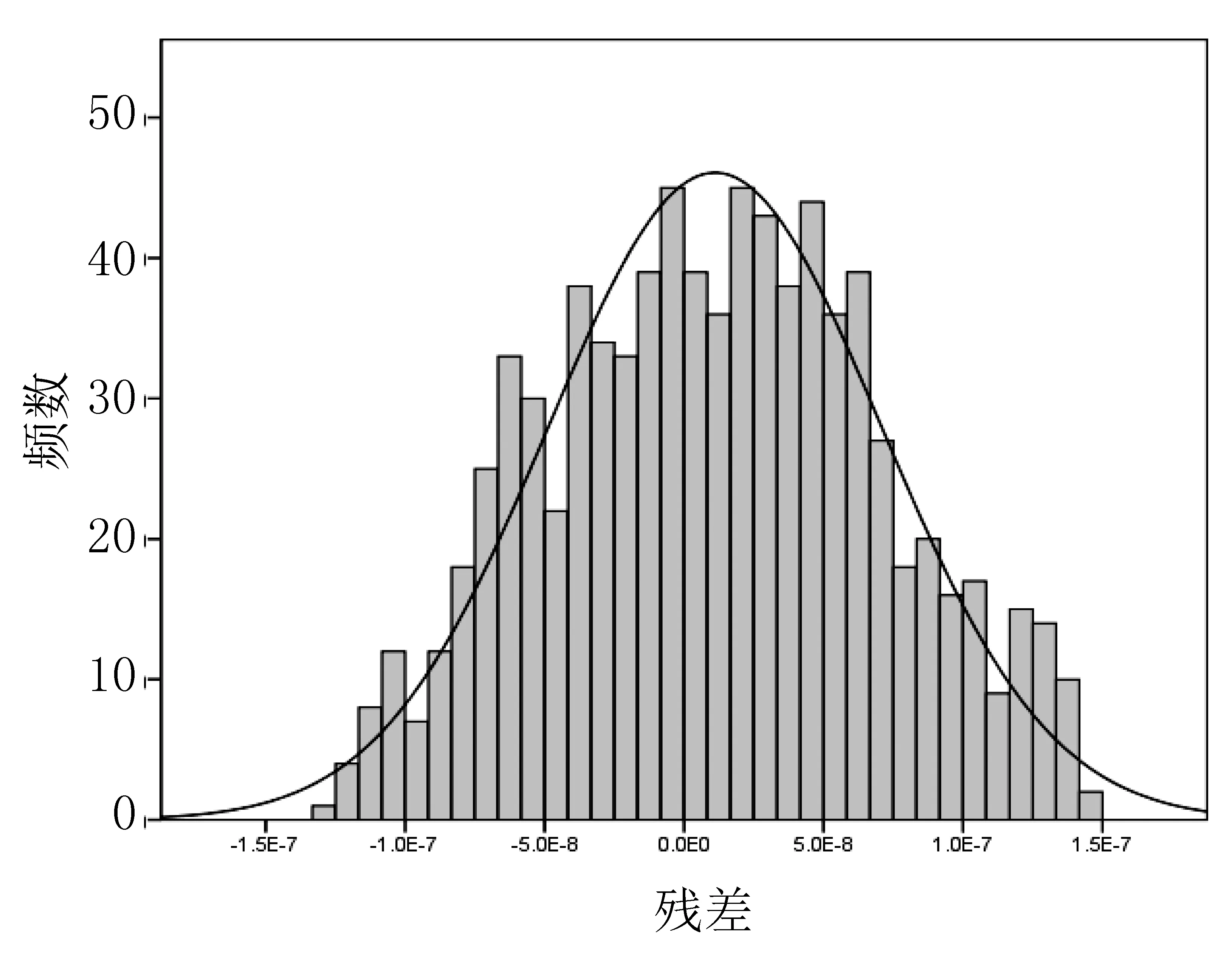
图1 柞树生长模型残差直方图Fig.1 Residual histogram of growth model of Quercus mongolica

表6为白桦的模型拟合过程，最终进入模型的变量也是9个，调整复相关系数为0.66。模型拟合结果见表7。

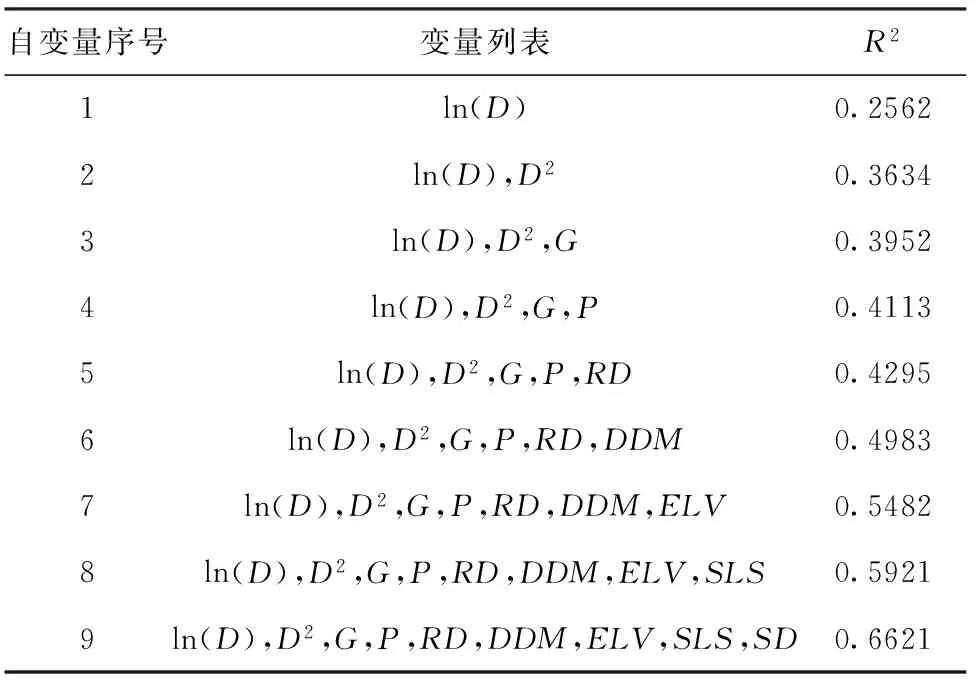
表6 白桦单木生长模型拟合过程

模型表达式为：

ln(dg)=-0.210+1.521×ln(D)-0.215×D2-0.007×G-0.052×P+0.21×RD+0.136×DDM-0.214×ELV+0.002×SLS-0.015×SD

(14)

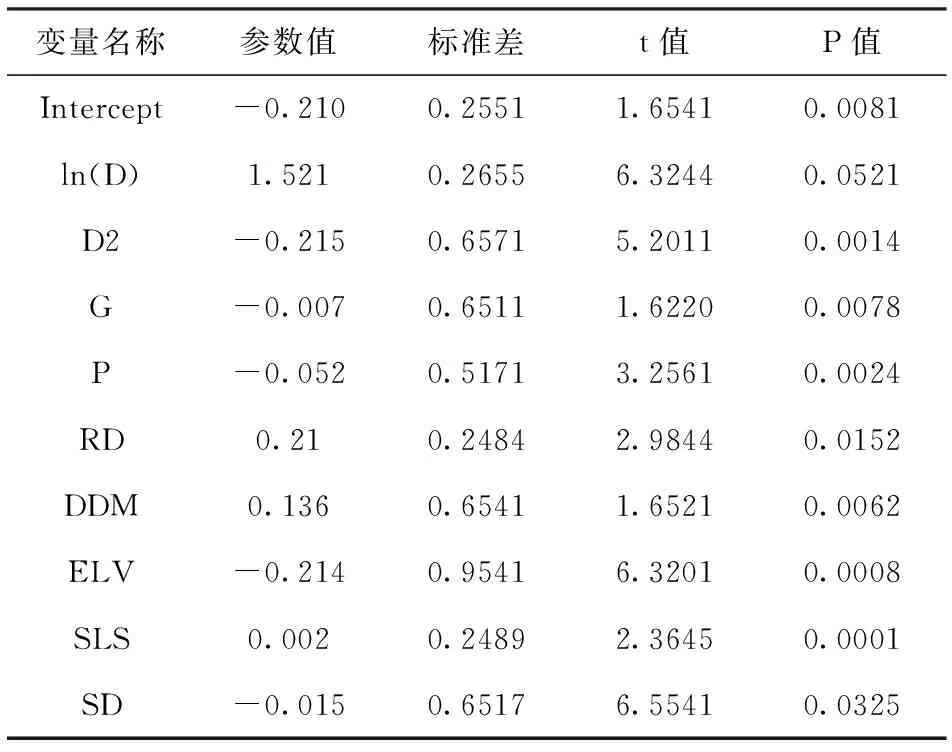
表7 白桦单木生长模型拟合结果

在白桦单木生长模型中,最终引入模型的自变量包括林木大小因子中的ln(D)和D2，竞争因子中的G、P、RD和DDM,立地因子中的ELV、SLS和SD,说明小兴安岭北部地区的白桦受林木大小、竞争因子和立地因子的影响都很大。

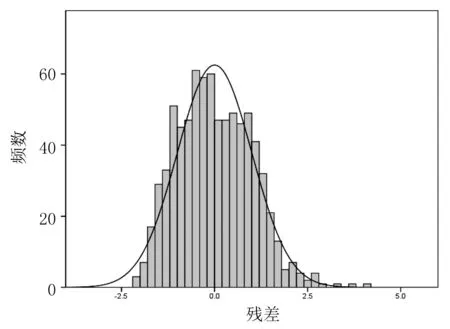
图2 白桦生长模型残差直方图Fig.2 Residual histogram of growth model of Betula platyphylla

图1为白桦生长模型的残差直方图，可以看出，残差服从近似正态分布，说明模型的拟合效果比较好。

表8为黑桦的模型拟合过程，最终进入模型的变量为7个，调整复相关系数为0.68，模型拟合结果见表9。

表8 黑桦单木生长模型拟合过程

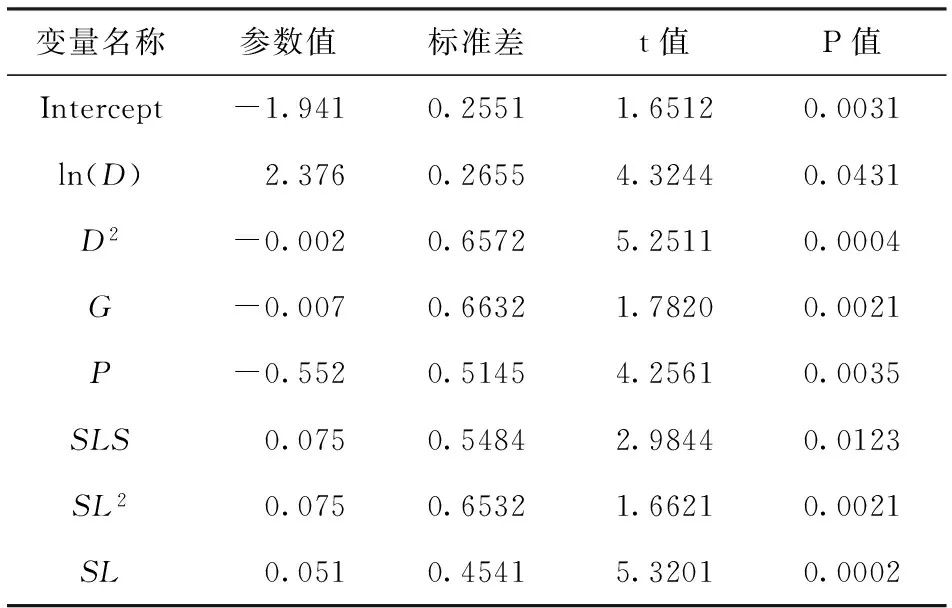
表9 黑桦单木生长模型拟合结果

模型表达式为：

ln(dg)=-1.941+2.376×ln(D)-0.002×D2-0.007×G-0.552×P+0.075×SLS+0.075×SL2+0.051×SL

(3)

在黑桦单木生长模型中,最终引入模型的自变量包括林木大小因子中的ln(D)和D2，竞争因子中的G和P,立地因子中的SLS、SL2和SL,说明小兴安岭北部地区的黑桦受林木大小、竞争因子和立地因子的影响都很大。

从黑桦生长模型的残差直方图3可以看出，残差服从近似正态分布，说明模型的拟合效果比较好。

4.2 单木枯损模型

采用自变量逐步引进的方法对模型12进行拟合，经自变量筛选得到柞树、白桦和黑桦的单木枯损模型。

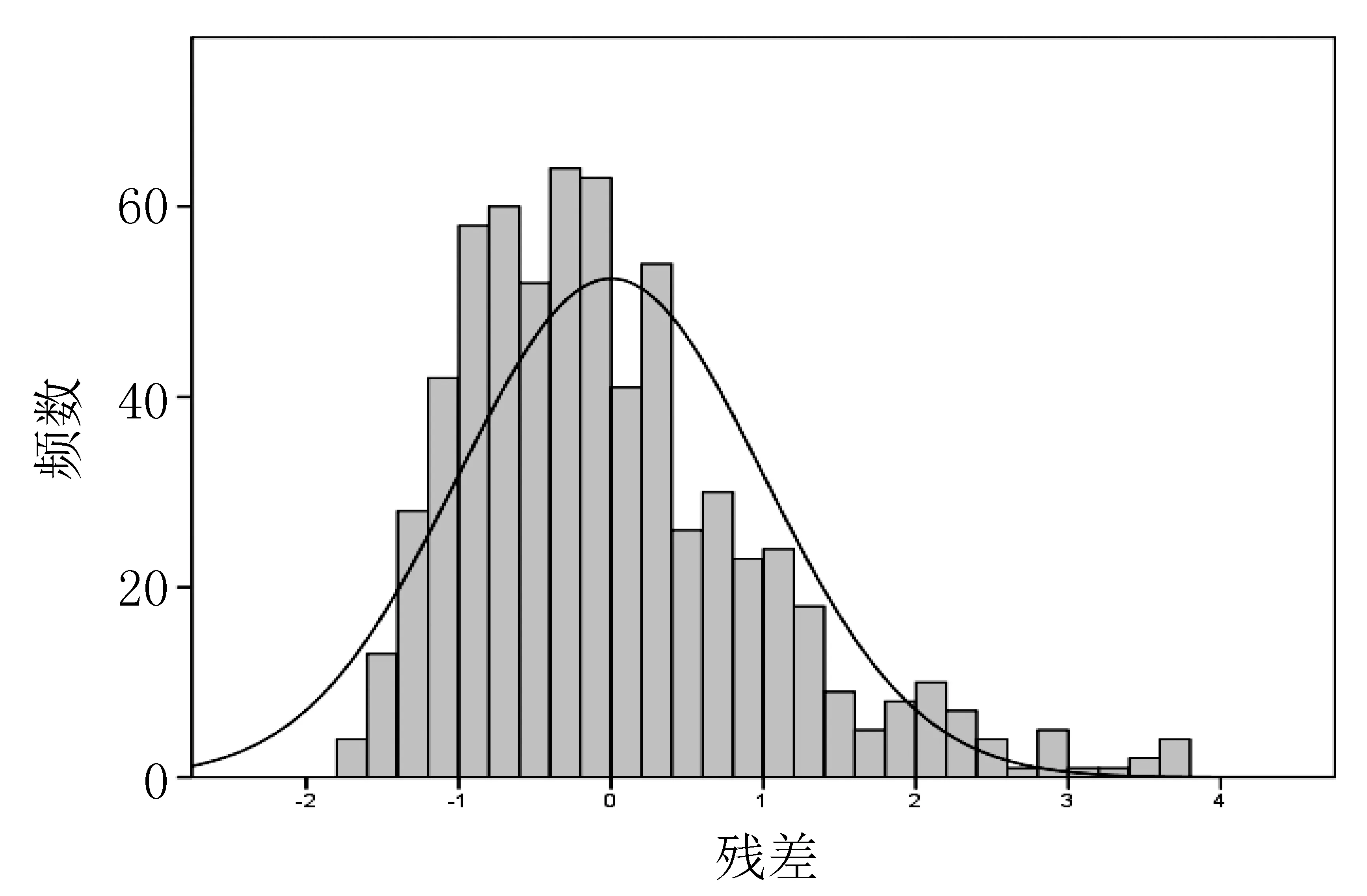
图3 黑桦生长模型残差直方图Fig.3 Residual histogram of growth model of Betula dahurica

在模型的拟合过程中，对各参数进行t检验，将不能通过t检验的参数剔除，最终得到相关系数较高且都通过t检验的各树种单木枯损模型(表10)。

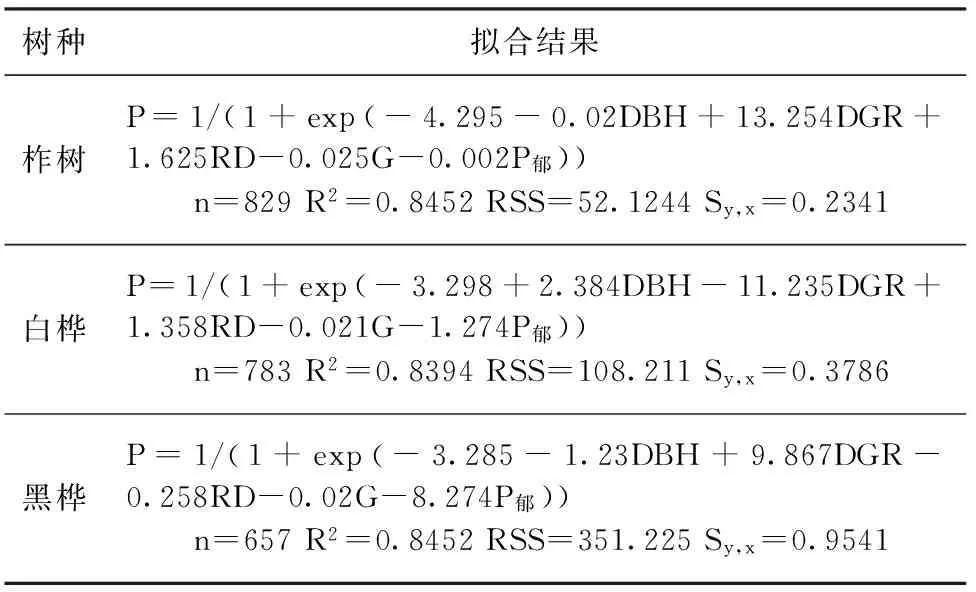
表10 枯损模型拟合

4.3 模型的检验

随机选出占总样本数20%的独立样本来对模型进行检验，评价直径生长量模型和枯损模型的预估效果。

4.3.1 单木生长模型的检验

将检验样本的自变量带入到拟合的经验方程中，得到各树种单木直径生长的估计值。将估计值和实测值进行检验，检验结果见表11。

从表11的统计结果可以看出，除柞树外白桦和黑桦的预估精度值都比较高，都通过了F检验，说明模型拟合良好。柞树没有通过F检验可能与竞争因子和立地条件等有关，测量误差导致的数据偏差也是导致模型没有通过检验的主要原因。

表11 单木生长模型统计量

4.3.2 单木枯损模型的检验

单木枯损模型的检验方法与单木生长模型相同，枯损样木检验结果见表12。

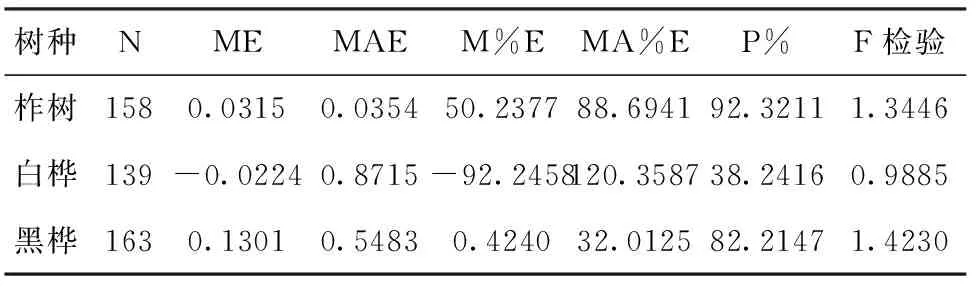
表12 单木枯损模型统计量

表12检验结果表明，所有模型都通过了F检验。

5 结论与讨论

建立了小兴安岭阔叶次生林优势树种的单木生长预估模型，对提高小兴安岭地区阔叶次生林管理水平，实现可持续经营具有重要的理论和现实意义。

各树种的单木模型的研究结果表明，林木直径大小因子ln(D)和D2是影响阔叶次生林主要树种单木直径生长量的最主要因素，ln(D)系数全部为正，说明直径(D)越大，定期直径生长量也越大。

大多数树种都通过了模型的F检验，说明本研究所建立的单木模型较好，可以很好地描述各树种林木的生长。对于没通过置信椭圆F检验的模型，应该从建模因子的选择和提高调查精度等方面加以改善。

各树种的单木枯损模型研究结果表明，林木的直径是影响林木枯损的最重要因子，直径越大，枯损概率越小。

[1] ZHAO D, BRUCE B, MACHELLE W. Individual tree diameter growth and mortality models for bottomland mixed species hardwood stands in the lower Mississippi alluvial valley [J]. Forest Ecology and Management, 2004, 199(2): 307-322.

[2] SULLIVAN A.D. and J. L. CLUTTER. A simultaneous growth and yield model for Loblolly Pine. For. Sci. 1972, 18: 76-86.

[3] WILLIAM R W. A basal area increment model for individual conifers in the Northern Rocky Mountains. Forest Science, 36(40): 1077-1104.

[4] 励龙昌. 以潜能函数建立单木生长模型[J]. 东北林业大学学报, 1990, 18(4)：22-28.

[5] 孟宪宇. 闽北杉木人工林单木模型[J]. 北京林业大学学报, 1996, 18(2): 1-7.

[6] 雷相东, 常敏, 陆元昌，等. 长白落叶松单木生长可视化系统设计与实现[J].计算机工程与应用, 2006(17):180-183.

[7] 葛宏立, 孟宪宇, 唐小明. 应用于森林资源连续清查的生长模型系统[J]. 林业科学研究, 2004, 17(4):413-419.

[8] 王文斗，李凤日，那冬晨，等 . 辽东栎单木生长模型的研究[J]. 林业科技，2005，30(2):11-13.

[9] 王孝安，段仁燕，王明利. 太白红杉单木胸径生长模型的研究[J]. 武汉植物学研究，2005，23(2):157-162.

[10] 闫明准，刘兆刚. 帽儿山地区次生林椴树单木胸高断面积生长模型的研究[J]. 森林工程，2009，25(2):1-4.

[11] 雷相东，李永慈，向玮 . 基于混合模型的单木断面积生长模型[J]. 林业科学，2009，45(1):74-80.

[12] 雷相东，李希菲 . 混交林生长模型研究进展[J]. 北京林业大学学报，2003，25(3):105-110.

[13] 葛宏立，项小强，何时珍，等 . 年龄隐含的生长模型在森林资源连续清查中的应用[J]. 林业科学研究，1997，10(4):420-424.

Establishment of Growth Model of Individual Typical Tree Species of Broad-leaved Secondary Forest in Lesser Khingan Mountains

WU Yao1, ZHANG Yichun1, QIN Kailun2，LIAN Yi3

(1.Heilongjiang Research Institute of Forestry, Harbin 150081, China; 2. Northeast Forestry University, Harbin 150040, China；3. Baihe Forestry Bureau, Yanbian, Jilin 133613, China)

This paper studied the typical tree species (poplar and birch forest, hardwood broadleaved forest) of broad-leaved secondary forest in Lesser Khingan Mountains, and established the growth model of the individual (Quercus mongolica, Betula platyphylla, Betula dahurica) to predict the growth of main tree species of broad-leaved secondary forest in Lesser Khingan Mountains and determine the growth conditions of individual tree directly. The results showed that the factor affecting the increment and mortality of the individual was tree diameter, which specifically reflected that the increment increased but the mortality decreased as the tree diameter increased.

broad-leaved secondary forest; growth model of individual tree; mortality model of individual tree; stand density; Lesser Khingan Mountains

10.3969/j.issn.1671-3168.2017.04.001

S711；S758.1

A

1671-3168(2017)04-0001-06

2017-01-06；

2017-04-17.

吴 瑶(1982-)，女，黑龙江大庆人，博士，副研究员.从事森林可持续经营研究.

秦凯伦(1980-)，男，博士研究生.