基于模糊神经网络的分数阶混沌系统的同步研究

沈细群，李安平

(1.湖南工程学院 电气信息学院，湘潭 411104；2.湖南工程学院 理学院，湘潭 411104)

基于模糊神经网络的分数阶混沌系统的同步研究

沈细群1，李安平2

(1.湖南工程学院 电气信息学院，湘潭 411104；2.湖南工程学院 理学院，湘潭 411104)

讨论一类不确定分数阶混沌系统的同步问题，基于连续频率分布等价模型、间接Lyapunov方法，利用模糊神经网络系统来近似未知函数，设计了一种鲁棒控制器，给出了混沌系统渐近同步的充分条件.仿真实例验证了方法的有效性.

分数阶混沌系统；同步；模糊神经网络；间接Lyapunov方法

0 引言

混沌系统在安全通信等领域有着巨大的应用价值，在对整数阶混沌系统进行讨论时，有学者发现混沌系统的阶数为分数时也会保持混沌，而通常讨论的整数阶混沌系统可以看成是分数阶混沌系统的特例，因此越来越多的学者们开始关注分数阶混沌系统.其中混沌系统同步是研究混沌系统的一个热门分支.

分数阶系统的稳定性理论是讨论分数阶系统的基础和最重要的问题，最近关于分数阶系统稳定的研究得到了很多相关的研究成果，这些成果大致可以分为两大类.一类是直接Lyapunov方法，文[1]利用Mittag-Leffler稳定性定义给出了分数阶系统的直接Lyapunov方法，另一类是间接Lyapunov方法，基于分数阶积分系统的等价连续频率分布模型文[2]给出了一种分数阶系统的间接Lyapunov方法.这些方法已经广泛用于稳定或控制分数阶系统.文献[3]针对一类非线性分数阶系统提出一种基于间接Lyapunov方法的非脆弱观测器设计方法.

由于在实际中系统由于干扰或各种其他因素的影响经常包含不确定，但是大多文献在讨论不确定分数阶系统控制时，对系统不确定项完全未知的讨论很少.由于模糊系统和神经网络的万能近似能力，其是处理不确定系统的一种重要方法，在整数阶系统控制中应用广泛，已经有很多的结果.而将模糊系统和神经网络应用到分数阶系统的控制文献较少，在我们的前期工作[4,5,6]利用间接Lyapunov方法讨论一类分数阶线性正实不确定系统的鲁棒渐近稳定的充分条件及基于神经网络和模糊神经网络的分数阶不确定非线性系统控制方法.而关于不确定分数阶混沌系统同步问题，文[7][8]基于自适应模糊算法给出一种控制方法实现对不确定混沌系统的控制.

在上述文献的基础上，讨论一类不确定分数阶混沌系统的模糊神经网络同步，基于连续频率分布等价模型、间接Lyapunov方法，利用模糊神经网络系统来近似未知函数，引入近似误差界的估计及控制补偿项，设计了一种鲁棒控制器，实现分数阶混沌系统同步，实例实现了不确定分数阶Chen系统的同步.理论和实验仿真说明了方法的有效性.

文中用到的一些数学符号，若X=(x1,x2,…,xn)T,Y=(y1,y2,…,yn)T, 则sign(X)表示(sign(x1),sign(x2),…,sign(xn))T, |X|表示(|x1|,|x2|,…,|xn|)T,X.*Y表示(x1y1,x2y2,…,xnyn)T.

1 问题描述

考虑下面分数阶混沌系统

Dαx(t)=f(x(t))

(1)

Dαy(t)=f(y(t))+d(t)+u(t)

(2)

其中x=(x1,x2,…,xn)T,y=(y1,y2,…,yn)T分别为驱动系统和响应系统的状态变量，α为分数阶数，0<α<1.函数f:Rn→Rn为未知而有界函数，d(t):R→Rn是外部有界干扰，u:R→Rn是连续的控制输入. 记ei(t)=yi(t)-xi(t)(1≤i≤n)，e(t)=(e1(t),e2(t),…,en(t))T为同步误差向量.

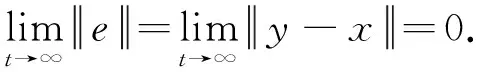
下面给出在下文中要用到的一些基本定义和引理[3][9].

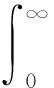
定义1 函数f(x)的q阶RL分数阶微分为

(3)

引理1 分数阶非线性微分方程

(4)

利用分数阶积分的连续频率分布模型，可表示为:

(5)

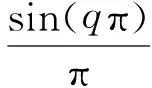
利用引理1，容易得到如下引理.

引理2 设系统Dαe=Ae，其中A=diag(-k1,-k2,…,-kn),ki>0，则系统渐近稳定.

(6)

2 主要结论

为实现分数阶混沌驱动系统(1)和响应分数阶混沌系统(2)之间的同步，引入负定对角矩阵A=diag(-k1,-k2,…,-kn)，则驱动系统和响应系统化为

Dαx(t)=Ax(t)+g(x(t))

(7)

Dαy(t)=Ay(t)+g(y(t))+d(t)+u(t)

(8)

同步误差方程为

Dαe=Ae+g(y(t))-g(x(t))+d(t)+u(t)

(9)

当系统函数及外部干扰已知时，取控制量为

u(t)=-g(y(t))+g(x(t))-d(t)

(10)

则得同步误差系统为Dαe=Ae.由引理2知系统渐近稳定，即实现混沌系统的同步.

(11)

(12)

控制器取为

(13)

从而原同步误差系统(11)化为

(14)

下面分别取参数更新率、控制补偿、误差界估计的自适应率如下

(15)

(16)

(17)

(18)

其中P是正定矩阵，uc为控制补偿项，ηW,ηE>0为常数.

定理1不确定响应分数阶混沌系统(2)在控制器(13)，控制补偿为(17)，误差界自适应率为(18)，模糊神经网络参数自适应率为(15，16)的控制下，系统同步到驱动混沌系统(1).

证明：由引理1系统(14) 等价为无穷维整数阶系统，

(19)

记v(w,t)=ZT(w,t)PZ(w,t)，P为正定矩阵.取Lyapunov函数为

(20)

沿着系统(14)的解轨迹关于t求导，得

(21)

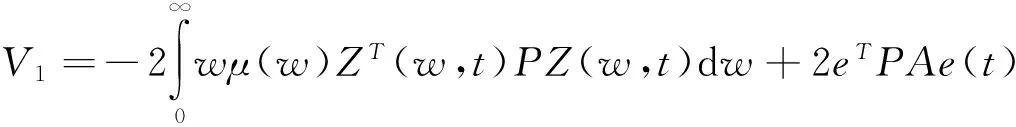
(22)

(23)

(24)

由P是正定矩阵，A是负定矩阵，及μ(w) 的定义，容易知道V1≤0

(25)

将控制补偿(17)及误差界估计的自适应率(18)代入(24)得

(26)

由(15,16) 代入(23),有

(27)

3 数值仿真

考虑分数阶驱动及响应混沌系统分别为如下Chen系统：

(28)

(29)

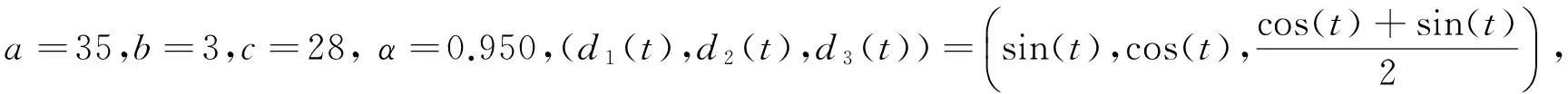
图1给出了驱动混沌系统的混沌吸引振子(x1x2图,x2x3图,x1x3图)，图2给出不确定响应混沌系统在模糊神经网络控制下与驱动系统间同步误差图像，从图像上可以看出，两个混沌系统很快实现渐近同步.

图1 分数阶混沌驱动系统

4 结论

本文针对一类分数阶不确定混沌系统同步问题给出一种基于模糊神经网络同步方法.系统不确定非线性函数完全未知，不需要任何先验信息，利用了分数阶系统的连续频率分布模型，模糊神经网络，间接Lyapunov方法获得了系统同步的充分条件，最后，给出数值例子表明了所给方法的有效性.

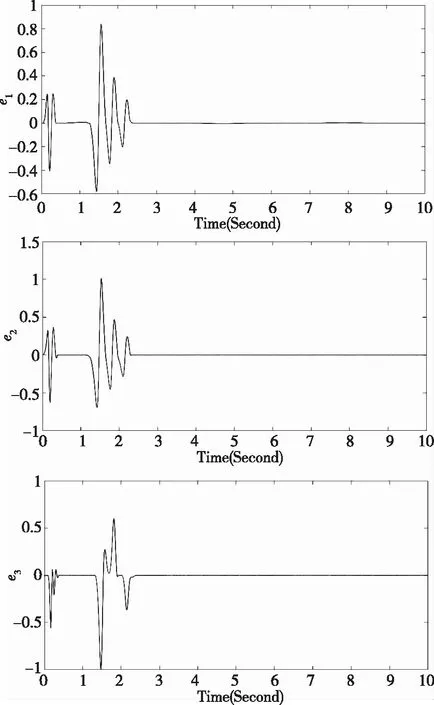
图2 混沌系统的同步误差

[1] Li Y，Chen Y Q，Podlubny I. Mitta-Leffler Stability of Ractional-order Nonlinear Dynamic Systems[J]. Automatica，2009，45(8)：1965-1969.

[2] Trigeassou J C，Maamri N，Sabatier J，et al.A Lyapunov Approach to the Stability of Fractional Differential Equations[J]. Signal Process，2011，91(3)：437-445.

[3] Lan Y H，Zhou Y.Non-fragile Observer-based Robust Control for a Class of Fractional-order Nonlinear Systems[J]. Systems & Control Letters，2013，62(12)：1143-1150.

[4] Li, Anping, Liu, Guorong, Luo, Yiping, Yang, Xiaoliang Shen Xiqun. Robust Fuzzy Neural Network Control for a Class of Nonlinear Fractional-order System[J]. Journal of Computational Information Systems, 2015, 11(20): 7347-7357.

[5] 李安平,刘国荣,杨小亮,等.一类非等阶分数阶非线性系统的神经网络控制[J].计算机工程与应用,2015,51(20):240-245.

[6] Li, Anping, Liu, Guorong, Luo, Yiping, Yang, Xiaoliang. An Indirect Lyapunov Approach to Robust Stabilization for a Class of Linear Fractional-order System with Positive Real Uncertainty[J]. Journal of Applied Mathematics and Computing, 2017, 43.doi:10.1007/s12190-017-1093-4.

[7] Lin T C， Kuo C H. Synchronization of Uncertain Fractional Order Chaotic Systems：Adaptive Fuzzy Approach[J]. ISA Transactions, 2011, 50(4): 548-556.

[8] Aghababa M P. Comments on“Synchronization of Uncertain Fractional Order Chaotic Systems：Adaptive Fuzzy Approach”[ISA Trans 50(2011) 548-556][J]. ISA Trans-actions, 2011,51(1)：11-12.

[9] Podlubny I. Fractional Differential Equations[M]. New York：Academic Press，1999.

SynchronizationofaClassofFractional-orderChaoticSystemBasedonFNNApproach

SHEN Xi-qun1, LI An-ping2

(1. College of Electrical and Information, Hunan Institute of Engineering, Xiangtan 411104, China;2. College of Science, Hunan Institute of Engineering, Xiangtan 411104, China)

The paper deals with the problem of synchronization of a class of fractional-order uncertain chaotic system. Based on a continuous frequency distributed model and indirect Lyapunov approach, the unknown functions have been approximated by using fuzzy neural networks. Then the robust controller and the sufficient condition for asymptotic synchronization of the driver chaos system and respond chaos system are presented. The validity of the proposed method is demonstrated by numerical example.

fractional-order chaotic system; synchronization; fuzzy neural network; indirect lyapunov approach

TP273

A

1671-119X(2017)03-0011-05

2017-04-02

湖南省教育厅基金项目(14C0288)；湖南工程学院校级科研基金项目(201402).

沈细群(1975-)，女，硕士，讲师，研究方向：混沌系统同步与智能控制.