基于拉格朗日一次插值的船舶故障录波时间同步

黄磊明，王黎明，陈钟琴

(1.海军工程大学 电气工程学院，武汉 430000； 2.中南民族大学 计算机科学学院，武汉 430070)

(*通信作者电子邮箱18674086511@163.com)

基于拉格朗日一次插值的船舶故障录波时间同步

黄磊明1*，王黎明1，陈钟琴2

(1.海军工程大学 电气工程学院，武汉 430000； 2.中南民族大学 计算机科学学院，武汉 430070)

(*通信作者电子邮箱18674086511@163.com)

针对外部时钟同步法在船用条件下存在的难以实施、易受干扰、安全性低等问题，提出一种基于插值算法的船舶故障录波时间同步方式。首先，录波主机从合并单元上传的报文中提取出原始采样值和额定延时信息；然后，经时间修正还原真实的采样时刻；最后，利用拉格朗日一次插值运算得到同步时刻的重采样值。Matlab仿真实验表明，幅值误差可以通过适当提高采样频率的方式降低，相位误差对应的等效时延均不超过2 μs；样机实验结果显示，正常条件下有效值误差不超过±0.01%，加入故障信号后，基波和5次谐波的有效值误差分别低于±0.006%和-0.5%，两种情况下的等效时延均不超过-3.5 μs，同步精度达到了IEC61850规定的T4等级。

故障录波；时间同步；外部时钟；拉格朗日一次插值；IEC61850

0 引言

故障录波装置是一种在国家电网中普遍使用的智能设备，可完整记录下故障发生前后的暂态过程[1]，从而为快速定位故障线路和准确判断故障原因提供原始参考。如果能将其应用于船舶电力监控领域，无疑会大大提高管理人员的工作效率，为船舶的安全稳定运行保驾护航。由于船舶电力系统的绝大部分参数都是随时间变化的，不同采样通道的电流、电压等离散数据只有对应于同一时刻才能代入分析算法之中进行故障诊断，这就涉及到了时间同步的问题。虽然外部时钟同步法在陆用故障录波装置中的应用已经非常成熟，但在船用条件下存在较大的局限性。本文首次将插值算法引入到录波数据的时间同步中，并通过仿真分析和样机实验证实了拉格朗日一次插值同步的可行性，从而提高了故障录波装置的海上适应能力。

1 外部时钟同步法的局限性分析

外部时钟同步法[2]在陆用故障录波装置中应用较多，其工作原理如图1所示。通过为电站配置授时信号接收器，并以此作为主时钟通过时钟服务器输出精确的秒脉冲信号和世界协调时[3]。合并单元在收到秒脉冲信号后，校准自身的内部时钟来与主时钟取得同步，之后再利用内部晶振的倍频功能来控制与其连接的电子式互感器进行高频同步采样。各合并单元按照统一的时间间隔通过交换机向录波主机发送包含采样时间的报文数据，录波主机根据内部的整定条件决定是否启动录波功能。

虽然该方式保证了时间信息在源头上是一致的，但其在可行性、可靠性、安全性等方面依然存在以下不足：

1)目前，船舶上安装的卫星信号接收系统主要是为导航定位服务的，时间同步的功能尚未开发，即使加装了时钟服务器，安放于舱底的故障录波装置要接入甲板上层的主时钟信号也非常麻烦。

2)海洋气候条件复杂多变，且船舶电力环境相对恶劣，采用无线传输的卫星同步信号很容易丢失或受到干扰，从而导致整个系统的时间信息发生紊乱，无法准确记录故障信息。

3)一旦接收机或时钟服务器发生故障，将导致整个同步网络瘫痪，而且录波主机需要配置额外的时钟输入接口[4]和高精度守时晶振，增加了装置的设计难度和硬件成本。

4)同步信号一般取自卫星系统，其中全球定位系统(Global Positioning System, GPS)信号受美国国防部控制[5]，不符合国家安全发展战略，中国自主研发的北斗卫星导航系统(BeiDou Navigation Satellite System, BDS)目前也仅限于服务亚太地区[6]，降低了其在跨国运输和远海作业中的应用。

鉴于外部时钟同步法在船用条件下存在诸多不足，本文探讨了如何通过插值算法实现船舶故障录波的数据同步，并对拉格朗日一次插值的精度进行了仿真分析和样机实验。

2 录波数据插值同步的实现方法

插值同步的核心思想是利用原函数f(t)在某个时间间隔内采样得到的若干个相邻的函数值，通过选择适当的拟合函数来估计该区间内其他任意时刻的采样值[7]，如图2所示。假设T为同步时刻，分别利用T时刻前后的两组原始采样值{(T1n，X1n)}和{(T2n，X2n)}，经过插值运算即可估计出重采样时刻T的同步数据X1和X2。

图2 录波数据插值重采样同步Fig. 2 Interpolation resampling synchronization of fault recording data

插值同步在船舶故障录波装置中的实现方式如图3所示：对于单台合并单元(Merging Unit, MU)来说，各通道的电流、电压信号按照相同的采样时刻进行模拟量/数字量(Analog/Digital, A/D)转换，从而实现了间隔内的数据同步；但是对于不同的合并单元来说，虽然采样频率可以保持一致，但对应的时间基准可能产生错位，这就需要录波主机对跨间隔的采样数据进行重采样，其中就涉及到插值同步的处理。录波主机在收到合并单元MU1和MU2上传的报文后，从中解析出采样序号、采样值、延迟时间等信息，利用接收时刻tan、tbn减去额定延时Δt即可还原实际的采样时刻tan′、tbn′；然后，录波主机的内部时钟分频产生重采样脉冲信号，根据重采样时刻tan″、tbn″与前后几个参考时刻tan′、tbn′之间的函数关系进行插值运算就可以得到一个“同步采样值”。按照固定的时间间隔重采样点不断后移，最终得到一个新的采样序列。

图3 插值同步的重采样过程Fig. 3 Resampling process of interpolation synchronization

插值同步方式通过软件算法即可实现录波数据的时间对齐[8]，摆脱了对外部时钟源的依赖，受气象条件、天线安装、电磁干扰等因素的影响较少，可靠性高，更加适用于海上复杂恶劣的工作条件。同时，该方式不需要连接时钟服务器和添加对时模块，简化了网络结构和硬件配置，避免了因中间环节发生故障带来的风险。

由于插值同步是通过函数拟合的方式近似求得同步时刻的采样值，因此存在一定的估值误差[9]。而不同的插值算法其误差大小、复杂程度和适用范围也不尽相同，例如拉格朗日插值、牛顿插值、埃尔米特插值、最小二乘法等[10]。其中，埃尔米特插值因同时满足在同步节点处的估值及导数与真实值相等[11]，所以得到了广泛的分析研究，但其精度的提高以运算量的增加为代价，理论上可行，但不适合工程实现。由于录波主机接入的采样通道可以达到上百路，并且采样频率通常在几千赫兹，如果采用埃尔米特插值等复杂算法，现场可编程门阵列(Field-Programmable Gate Array, FPGA)和中央处理器(Central Processing Unit, CPU)需要处理的数据量过大，将直接影响到故障录波装置的实时响应和稳定运行。因此，从估值精度、计算量和实现的难易程度综合考虑，本文提出了基于拉格朗日一次插值算法的船舶故障录波时间同步方式，首次将插值算法应用到录波数据的同步当中，并对由此引起的幅值误差和相位误差进行了分析。

3 拉格朗日一次插值同步仿真分析

假设录波主机接收到同一个合并单元发送的两个相邻采样间隔的报文数据，并通过解码提取和时间修正获得了某个电流通道的两个离散点[tk,i(tk)]和[tk+1,i(tk+1)]。利用拉格朗日一次插值算法[12]可以获得同步时刻t所对应的电流值:

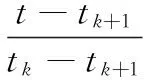
(1)

作为实际值i(t)的近似，拉格朗日一次插值的误差为:

(2)

其中：i″(ξ)为i(t)的二阶导数，ξ为[tk,tk+1]的某个时刻。

为了检验拉格朗日一次插值算法的同步精度，本文利用Matlab进行了仿真分析。假设合并单元的采样频率为1 kHz，即工频条件(f=50 Hz)下每周波有20个采样点，且输入的电流信号中包含直流、基波和3次谐波成分：

i(t)=0.3+5 cos(2πft)+1.7 cos(6πft+π/30)

(3)

录波主机在收到不同间隔发送的采样值报文后，仍以1 kHz的频率进行重采样，即每隔1 ms进行一次数据同步，且同步点与参考点的时间差为t-tk=2 μs。按照拉格朗日一次插值的计算方法，每两个相邻时刻的源采样值便可求出一个同步数据，一周波的仿真结果如图4所示。

通过观察可以发现，绝对误差的大小随着两个相邻原始采样点之间波形的曲率而变化，区间内的线性度越好绝对误差越小，在曲率较大的位置绝对误差增大。除了极个别点以外，相对误差基本上不超过0.45%。表1列出了i(t)在1 kHz采样频率下由拉格朗日一次插值引起的一周波最大绝对误差和最大相对误差。

图4 拉格朗日一次插值实验误差分析(N=20)Fig. 4 Error analysis of Lagrange once interpolation experiment (N=20)表1 拉格朗日一次插值实验最大误差分析(N=20)Tab. 1 Maximum error analysis of Lagrange once interpolation (N=20)

误差t/si(t)/AL1(t)/AΔi(t)/A[Δi(t)/i(t)]/%最大绝对误差0.010002-6.390348-6.3885160.001832-0.0287最大相对误差0.0140020.0191030.0184690.0006343.3189

利用Matlab的快速傅里叶变换(Fast Fourier Transform, FFT)函数fft(X,n)对上文中由拉格朗日一次插值得到的20个同步点进行幅度和相位分析，如图5所示。

图5 拉格朗日一次插值实验FFT分析(N=20)Fig. 5 FFT analysis of Lagrange once interpolation experiment (N=20)

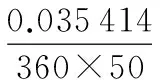
假设原始电流信号保持不变，合并单元的采样频率和录波主机的重采样频率提高至4 kHz，即工频条件下每周波有80个采样点，且同步点与参考点的时间差仍为t-tk=2 μs，则一周波的拉格朗日一次插值仿真结果如图6所示。从图6中可以更加清楚地看出3次谐波成分对拉格朗日一次插值绝对误差的影响，两者的变化基本保持同步。同时，采样频率的提高使得拉格朗日一次插值的误差进一步变小，绝对误差降至0.000 5以下，相对误差则大部分不超过0.15%。

表2 幅度误差分析(N=20)Tab. 2 Error analysis of amplitude (N=20)

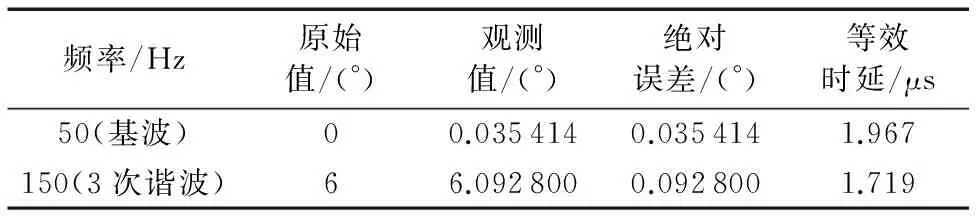
表3 相位误差分析(N=20)Tab. 3 Error analysis of phase (N=20)

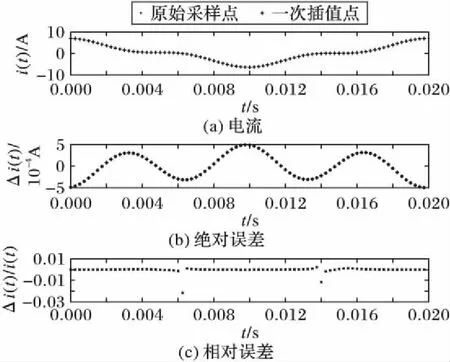
图6 拉格朗日一次插值实验误差分析(N=80)Fig. 6 Error analysis of Lagrange once interpolation experiment (N=80)

表4对4 kHz采样频率下拉格朗日一次插值的最大误差进行了分析，与表1相比，采样率提高了4倍之后，拉格朗日一次插值的精度得到了明显的改善。

在得到了80个插值点数据[t,L1(t)]之后，同样对其进行FFT分析，如图7所示。从幅度—频率谱可以看出，原始信号中的直流、基波和3次谐波三种成分得到了很好的分离还原，幅度的观测值与原始值更加接近，绝对误差和相对误差可以控制在相当低的水平(见表5)。相位—频率谱中50 Hz(基波)和150 Hz(3次谐波)处的相位观测值与原始值分别相差0.035 964°和0.107°，对应的等效时延均不超过2 μs(见表6)，同步精度满足IEC61850标准。

表4 拉格朗日一次插值实验最大误差分析(N=80)Tab. 4 Maximum error analysis of Lagrange once interpolation (N=80)

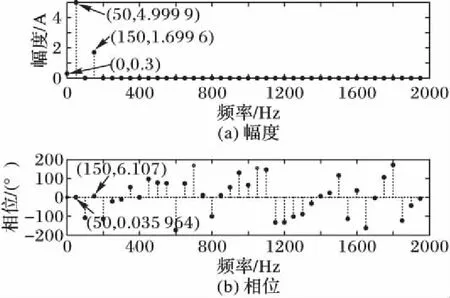
图7 拉格朗日一次插值实验FFT分析(N=80)Fig. 7 FFT analysis of Lagrange once interpolation experiment (N=80)表5 幅度误差分析(N=80)Tab. 5 Error analysis of amplitude (N=80)

频率/Hz原始值/A观测值/A绝对误差/A相对误差/%0(直流)0.30.30000.00000.00050(基波)5.04.9999-0.0001-0.002150(3次谐波)1.71.6996-0.0004-0.024

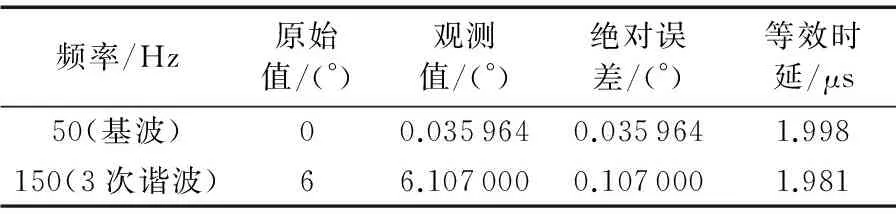
表6 相位误差分析(N=80)Tab. 6 Error analysis of phase (N=80)

综上所述，虽然拉格朗日一次插值的误差大小受波形暂态变化的影响较大，但当采样频率较高时，参考点的时间间隔[tk,tk+1]可以很小，此时相邻的两个采样值之间的波形接近一条直线，拉格朗日一次插值结果引起的估值误差可以降到很低，同步精度能够达到IEC61850规定的T4等级，满足后期故障分析的要求。同时，拉格朗日一次插值只需要用到相邻的两个采样值就可以实现数据同步，计算起来比较方便，在硬件设计上容易实现。

4 拉格朗日一次插值同步样机实验

结合船舶电力系统的工作特点，在对故障录波的时间同步技术进行了研究和改进之后，本文自主设计了一套海工故障录波装置-I型(HaiGong Fault Recording Device-I, HGFR-I)船舶电力故障录波样机，并通过搭建实验平台对样机的性能指标进行了相关测试，如图8所示。

由于船舶电力系统中的一次互感器输出的电压、电流信号不是很高，因此本文选用传统的继电保护测试仪产生合并单元的输入信号。合并单元通过光纤将数字化的采样数据传输至录波主机，如果插值同步后的采样值达到了录波的启动条件，会按照设置的录波时序进行数据存储。上位机的录波分析软件能够实时监测各个采样通道的运行状态，并将存储于录波主机中的文件提取出来进行离线分析。

图8 录波样机实验平台Fig. 8 Test platform of fault recording prototype

4.1 正常条件下的同步精度实验

利用继电保护测试仪的交直流测试模块输出有效值为57.7 V、频率为50 Hz、相角依次相差120°的额定三相交流电压信号，分别接入3台合并单元的交流电压通道进行4 kHz采样，录波主机按照相同的频率重采样实现时间同步。通过手动录波功能，可以对正常条件下任意时刻的同步测量值进行离线分析，这里随机选取了T1、T2时刻的两组数据，如图9所示。

由于拉格朗日一次插值是一种估值算法，因此会存在一定的误差。表7列出了在T1、T2时刻三相交流电压有效值的测算结果，可以看出正常条件下拉格朗日一次插值后的实测值与原始值之间的绝对误差和相对误差都很小，分别维持在±0.01 V和±0.01%以下，其精度可以满足分析需要。

表7 正常条件下有效值误差分析Tab. 7 RMS error analysis under normal condition

表8列出了在T1、T2时刻三相交流电压的相位误差，以A相为基准，继电保护测试仪输出的原始信号相位差依次为0°、-120°、120°，经过拉格朗日一次插值同步后，产生了微小的相位偏移，但都未超过-0.060°，对应的等效时延(经系统修正后)均不超过-3.5 μs，同步精度可以达到IEC61850标准规定的T4等级即±4 μs。

表8 正常条件下相位误差分析Tab. 8 Phase error analysis under normal condition

4.2 发生故障时的同步精度实验

在验证了电网正常运行状态下的数据传输和时间同步符合要求之后，保持继电保护测试仪的输出电压有效值不变，将1#母线电压Ua、Ub、Uc的5次谐波越限定值修改为10.0%，如图10所示。

图10 5次谐波电压越限定值Fig. 10 Set up ceiling of the fifth harmonic voltage

由继电保护测试仪的谐波实验模块向1#母线电压的三个通道同时加入10.103%的5次谐波成分，如表9所示。真有效值、基波有效值和5次谐波有效值分别为57.7 V、57.408 V和5.8 V，基波和5次谐波的三相之间的相位差均为120°。

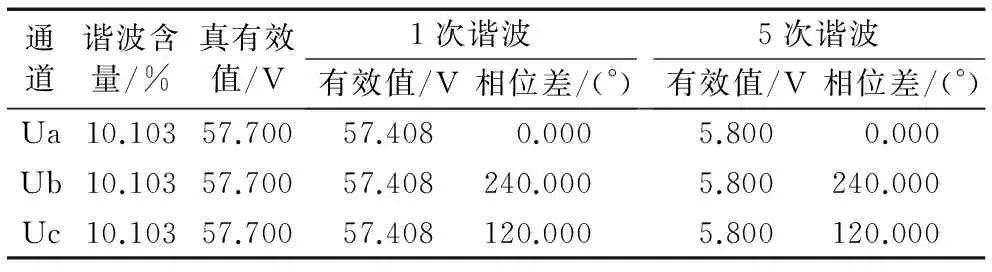
表9 5次谐波电压越限输出Tab. 9 Output of the fifth harmonic voltage over ceiling

录波样机通过全周波傅里叶算法[14]检测到电压信号中的5次谐波成分含量超过整定值10%，启动录波功能，生成包含故障信息的录波文件，如图11所示。

图11 5次谐波电压越限启动录波Fig. 11 The fifth harmonic voltage over ceiling trigger fault recording

通过上位机软件的“通道组合分析”菜单中包含的“谐波分析”选项，可以将5次谐波越限启动录波文件中记录的基波和谐波成分以图形加表格的方式表示出来，如图12所示，从中能够直观地看出故障发生前后电压波形的变化过程以及不同时刻的有效值和相位信息，并通过全周波傅里叶算法将其中包含的主要谐波成分快速提取出来。

表10列出了在任意挑选的两个时刻三相交流电压有效值误差的计算结果，可以看出：

1)继电保护测试仪输出的三相电压信号真有效值均为57.7 V，经拉格朗日一次插值后得到的实测值与原始值非常接近，最大绝对误差不超过-0.005 V，最大相对误差不超过-0.01%，几乎可以忽略不计。

2)基波的原始有效值为57.408 V，经拉格朗日一次插值和全周波傅里叶变换后的观测值大部分落在57.410 V左右，最大绝对误差不超过±0.004 V，最大相对误差不超过±0.006%。由此可以看出在故障条件下，拉格朗日一次插值引起的基波有效值误差很小，精度满足故障分析需求。

3)相比真有效值和基波有效值，5次谐波的实测有效值误差稍大，基本上维持在-0.024 V左右，但并不影响故障分析。这里的误差偏大主要是由三方面原因造成的：一是受设备硬件指标的影响，继电保护测试仪输出的5次谐波信号精度要比基波低；二是5次谐波信号的曲率变化没有基波平稳，拉格朗日一次插值引起的估值误差随之增大；三是在用全周波傅里叶算法提取谐波信号的过程中，采用梯形法对积分公式进行近似求解时，谐波成分也会带来计算误差[15]。

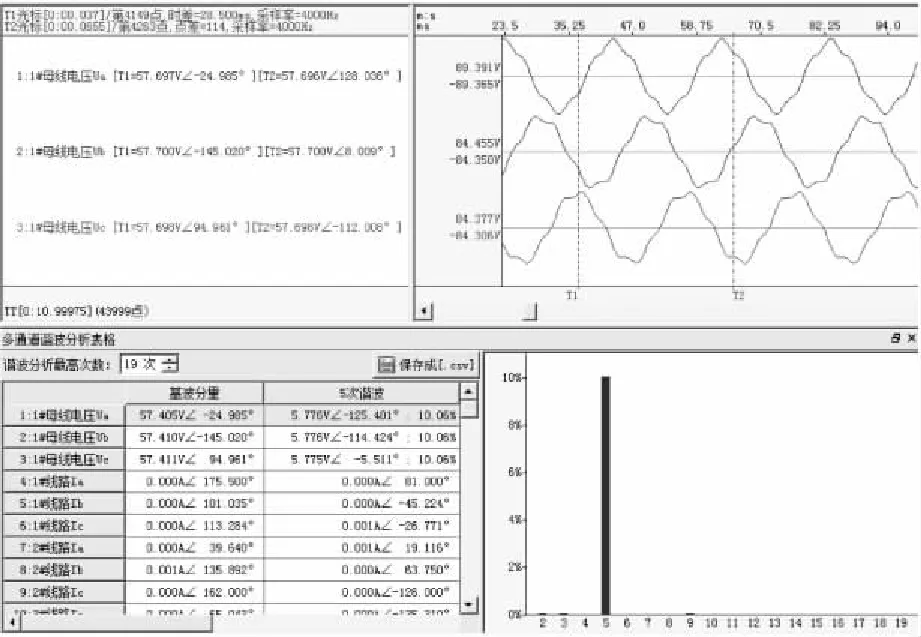
图12 5次谐波电压分析Fig. 12 Voltage analysis for the fifth harmonic表10 故障条件下有效值误差分析Tab. 10 RMS error analysis under fault condition

有效值时刻通道原始值/V实测值/V绝对误差/V相对误差/%真有效值基波有效值5次谐波有效值T1T2T1T2T1T2Ua57.70057.697-0.003-0.005Ub57.70057.7000.0000.000Uc57.70057.698-0.002-0.003Ua57.70057.696-0.004-0.007Ub57.70057.7000.0000.000Uc57.70057.698-0.002-0.003Ua57.40857.405-0.003-0.005Ub57.40857.4100.0020.003Uc57.40857.4110.0030.005Ua57.40857.406-0.002-0.003Ub57.40857.4100.0020.003Uc57.40857.4100.0020.003Ua5.8005.776-0.024-0.414Ub5.8005.776-0.024-0.414Uc5.8005.775-0.025-0.431Ua5.8005.776-0.024-0.414Ub5.8005.777-0.023-0.397Uc5.8005.776-0.024-0.414

表11列出了在故障条件下，T1、T2两个时刻三相交流电压相位误差的计算结果,可以看出：

1)以A相为基准，基波的原始相位差依次为0°、-120°和120°，实测相位差与原始相位差之间的绝对误差不超过-0.060°，相对误差低于±0.05%，对应的等效时延不超过-3.5 μs，基波成分的同步精度在IEC61850标准要求的范围之内。

2)由于5次谐波信号的频率较高，因此测量得到的相位精度要比基波稍差一些，绝对误差和相对误差分别不超过-0.200°和±0.200%，等效时延依然可以维持在-3 μs以下，符合IEC61850标准中的T4等级要求，插值结果同样可以用来分析电力信号中的谐波成分，不会造成故障的误判。

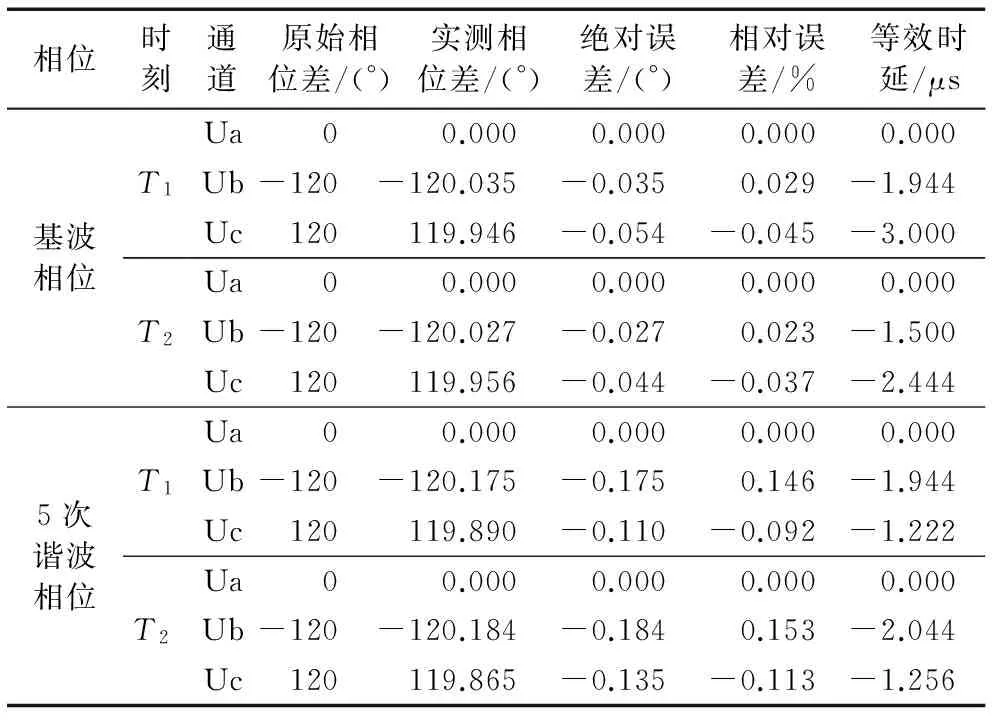
表11 故障条件下相位误差分析Tab. 11 Phase error analysis under fault condition

综上所述，无论是在正常条件下还是发生故障时，拉格朗日一次插值引起的有效值误差都很小，几乎可以忽略不计，基波和谐波的相位误差对应的等效延时均不超过-3.5 μs，能够达到IEC61850标准规定的T4等级，满足了故障录波对幅值和相位的测量精度要求。

5 结语

外部时钟同步法是目前陆用故障录波装置普遍采用的同步方法，由于该方式过度依赖外部主时钟，船用条件下对时信号难以获得，同步精度受外部因素影响较大，并且网络结构复杂、应用成本较高，因此本文提出了基于拉格朗日一次插值算法的船舶故障录波时间同步方式，并通过Matlab仿真和样机实验进行了可行性验证，结果显示在4 kHz采样频率下，有效值误差非常小，几乎可以忽略不计，相位误差对应的等效时延可以控制在IEC61850标准规定的±4 μs范围内，满足后期故障分析的精度要求。

References)

[1] 钱翰博.基于FPGA的分布式输电线路故障录波器的设计[D].南京:南京理工大学,2006.(QIAN H B. The design on fault recorder of distributed transmission line based on FPGA [D]. Nanjing: Nanjing University of Science and Technology, 2006.)

[2] SERIZAWA Y, KITAMURA K, MYOUJIN M, et al. SDH-based time synchronous system for power system communications [J]. IEEE Transactions on Power Delivery, 1998, 13(1): 59-65.

[3] 华煌圣,王莉.数字化变电站时间同步系统的探讨[J].电力系统通信,2011,32(219):28-32.(HUA H S, WANG L. The related issues about time synchronization system in digital substations[J]. Telecommunications for Electric Power System, 2011, 32(1): 28-32.)

[4] 方彦军,易凤飞,陈锐民,等.分段插值同步算法在数字化变电站中的应用[J].自动化与仪表,2013,28(2):1-5.(FANG Y J, YI F F, CHEN R M, et al. Application of piecewise interpolated synchronous algorithm in digital substation [J]. Automation & Instrumentation, 2013, 28(2): 1-5.)

[5] MATSUYAMA T, ABE K, KASHIWA R, et al. The change of the error by SA cancellation of GPS [J]. Research Memoirs of the Kobe Technical College, 2001,39: 103-106.

[6] TORO F G, BECKER U, FUENTES D E D, et al. Accuracy analysis for GNSS-based urban land vehicle localisation system [J]. IFAC-ParersOnLine, 2016, 49(3): 191-196.

[7] 吴超凡,陈隆道.基于分段插值同步化算法的谐波测量[J].电力系统保护与控制,2016,44(9):6-10.(WU C F, CHEN L D. Harmonic measurement based on piecewise interpolation synchronization algorithm [J]. Power System Protection & Control, 2016, 44(9): 6-10.)

[8] 向珉江,高厚磊,安艳秋,等.一种提高数据同步精度的自适应插值算法[J].电力系统自动化,2012,36(8):77-81.(XIANG M J, GAO H L, AN Y Q, et al. An adaptive interpolation algorithm to improve data synchronization precision [J]. Automation of Electric Power Systems, 2012,36(8):77-81.)

[9] 丁泉,李帅.智能变电站重采样应用研究及其线性插值法误差分析[J].电力系统保护与控制,2015,43(23):132-136.(DING Q, LI S. Application study on resampling in smart substation with error analysis of linear interpolation [J]. Power System Protection and Control, 2015,43(23):132-136.)

[10] 刘伟良,李辉,欧阳帆,等.智能变电站继电保护采样数据同步方法[J] .湖南电力,2013,33(S1):31-33.(LIU W L, LI H, OUYANG F, et al. Data synchronization method for relay protection of digital substation [J]. Hunan Electric Power, 2013, 33(S1): 31-33.)

[11] ZAROWSKI C J. An Introduction to Numerical Analysis for Electrical and Computer Engineers [M]. Hoboken, NJ: John Wiley and Sons, 2004: 251-289.

[12] CAI Q, SONG L Z. The Lagrange interpolation polynomial algorithm error analysis [C]// Proceedings of the 2011 International Conference on Computer Science and Service System. Piscataway, NJ: IEEE, 2011: 3719-3722.

[13] 姜雷,郑玉平,艾淑云,等.基于合并单元装置的高精度时间同步技术方案[J].电力系统自动化,2014,38(14):90-94.(JIANG L, ZHENG Y P, AI S Y, et al. A highly accurate time synchronization technology scheme based on merging unit [J]. Automation of Electric Power Systems, 2014, 38(14): 90-94.)

[14] 郑志萍,杨武盖,毛艳芳,等.间谐波对全周波傅里叶算法影响研究[J].电测与仪表,2015, 52(19): 30-35.(ZHENG Z P, YANG W G, MAO Y F, et al. Study on the influence of inter-harmonic on full-cycle Fourier algorithm [J]. Electrical Measurement & Instrumentation, 2015, 52(19): 30-35.)

[15] HARRIS F J. On the use of windows for harmonic analysis with the discrete Fourier transform [J]. Proceedings of the IEEE, 1978, 66(1): 51-83.

This work is partially supported by the National Natural Science Foundation of China (61101206) and the Postdoctoral Science Foundation of China (2015M572773).

HUANGLeiming, born in 1987, M. S. candidate, assistant engineer. His research interests include intelligent monitoring and controlling of ship, comprehensive model and application of ship power.

WANGLiming, born in 1978, Ph. D., associate professor. His research interests include automatic dispatch and management of power grid, design and development of embedded system.

CHENZhongqin, born in 1996. Her research interests include computer programming, artificial intelligence software.

TimesynchronizationofshipfaultrecordingdevicebasedonLagrangeonceinterpolation

HUANG Leiming1*, WANG Liming1, CHEN Zhongqin2

(1.CollegeofElectricalEngineering,NavalUniversityofEngineering,WuhanHubei430000,China；2.CollegeofComputerScience,South-CentralUniversityforNationalities,WuhanHubei430070,China)

Aiming at the problem that the external clock synchronization method is difficult to implement, susceptible to interference and insecure under the marine condition, a time synchronization method of ship fault recording device based on interpolation algorithm was proposed. Firstly, the recording host extracted the original sampling values and the rated delay information from the packets uploaded by the merging units. Secondly, the real sampling time was restored after time correction. Finally, Lagrange once interpolation operation was used to obtain the resampling values at the synchronous time. Simulation on Matlab shows that the amplitude error can be reduced by increasing the sampling frequency appropriately, and the equivalent delay corresponding to the phase error is not more than 2 μs. Prototype test shows that the error of valid values does not exceed ±0.01% under the normal condition, of which the fundamental and 5th harmonic are less than ±0.006% and -0.5% after adding the fault signal. Moreover, both of the equivalent delays are less than -3.5 μs, and the synchronization accuracy is in accordance with the T4 level specified in IEC61850.

fault recording; time synchronization; external clock; Lagrange once interpolation; IEC61850

TP274.2

A

2017- 03- 07;

2017- 05- 26。

国家自然科学基金资助项目(61101206)；中国博士后科学基金资助项目(2015M572773)。

黄磊明(1987—)，男，山东烟台人，助理工程师，硕士研究生，主要研究方向：舰船智能化监测与控制、舰船电力系统全面模型及其应用； 王黎明(1979—)，男，山东烟台人，副教授，博士，主要研究方向：电网自动化调度与管理、嵌入式系统设计与开发； 陈钟琴(1996—)，女，江西九江人，主要研究方向：计算机编程、人工智能软件。

1001- 9081(2017)08- 2427- 06

10.11772/j.issn.1001- 9081.2017.08.2427