柯西不等式的推论的应用

刘振兴

(佛山市第一中学，广东 佛山 528000)

柯西不等式的推论的应用

刘振兴

(佛山市第一中学，广东 佛山 528000)

柯西不等式是一个非常重要的不等式，它以其形式对称和谐美的结构引起了许多学者的研究,并出现了许多的推论变式.应用柯西不等式的推论，可以简单解决许多竞赛中的不等式问题,并且对这些不等式问题可进行推广.

柯西不等式；推论；推广

一、柯西不等式及其推论

柯西不等式:设ai,bi∈R(i=1,2,…,n),则

当且仅当ai=λbi(i=1,2,…,n)时,等号成立.

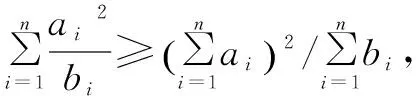
二、柯西不等式的推论的应用

a2+b2+c2+d2+(a+b+c+d)2≥[(1-t)a+(2-t)b+(3-t)c+(4-t)d+t(a+b+c+d)]2/[(1-t)2+(2-t)2+(3-t)2+(4-t)2+t2]

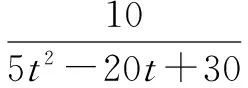
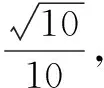
对例1可进行维数的推广.

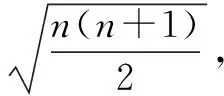
证明根据柯西不等式，类似例1过程得

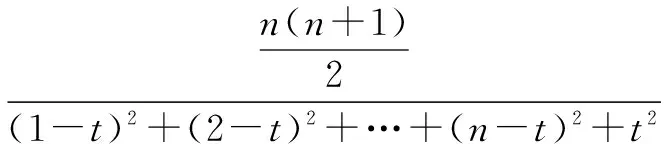
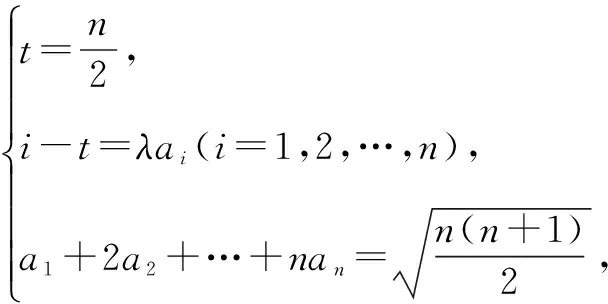
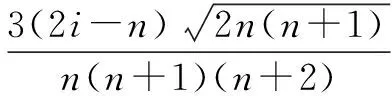
在解决有些不等式问题时,我们要多次使用柯西不等式的推论.

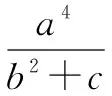
解由推论1得

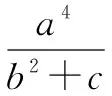
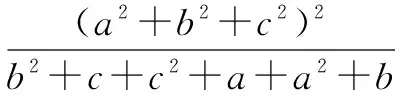
令a2+b2+c2=x,由推论1得

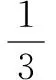
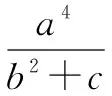
所以f(x)在[3,+)上单调递增,

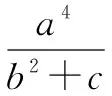
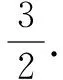
对例2可进行如下推广.

(1)维数的推广

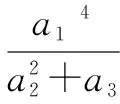
(2)幂的推广

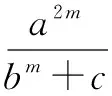
(3)线性推广

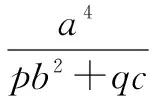
综合(1),(2),(3)可得一般性推广,并给出证明.

证明由推论1得

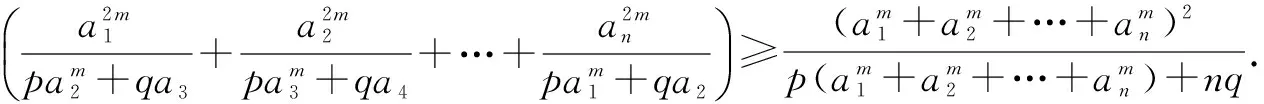
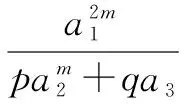
[1]卓书月.柯西不等式及其变式的应用[J].民营科技,2011(9):78,162.

G632

A

1008-0333(2017)22-0030-02

刘振兴(1989.1-)，男，江西赣州人，二级教师，从事高中数学教学与研究.

责任编辑：杨惠民]