高中物理临界问题的一点体会

孙瑞凝

(山东省肥城市泰西中学2016级16班，山东 肥城 271600)

高中物理临界问题的一点体会

孙瑞凝

(山东省肥城市泰西中学2016级16班，山东 肥城 271600)

高中物理的临界问题一直是高考中的热点，在临界问题的解决过程中，关键是确定临界术语，找出临界条件，问题就容易解决了.

高中物理；临界值问题；平衡

在高中物理的解题过程中，分析一个物理过程转变为另一个物理过程是经常遇到的，也就是临界问题.高中物理中的临界问题一直是高考中的热点.分析近几年的高考的物理典型题，不难发现对物理过程的临界问题考察一般是运用物理现象的临界状态分析.

在临界问题的解决过程中，关键是确定临界术语，找出临界条件，也要能够立足课本，确立高于课本的指导方针，对临界问题的概念和计算方法理解到位，不留盲点.在物理复习中，专题的练习大部分都是课本上的例题、习题，以及例题和习题的变式，所以要能够掌握基础知识和基础技能，精通课本.

对于临界值的求法，则有两种方法，一种是用物理规律求极值，例如，临界条件、边界条件等.第二种方法是用数学方法求极值，如不等式、二次函数、三角函数和解三角形等.

一、运动学和力学中常见的临界问题

例1 一辆货车以V0=8m/s的速度匀速行驶，经过一辆交警车旁的时候，交警发现该货车有违章行为，决定追赶并拦截，经过2.5s，警车发动，以加速度a=2m/s2做匀加速运动，则在警车追上货车之前，两车之间的最大距离是多少？

分析本题考察的是速度相等的临界条件，警车和货车的速度相等的时候，两车的距离是最远的.

解由题意可知，两车速度相等的时候，距离是最远的得v警=at,v货=v0，则v警=v货，

可以得到at1=v0

则两车相距较远的时候，警车所用的时间为

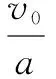
这是货车行驶的距离为：

x货=v0(t0+t1)=8×(2.5+4)m=52m

警车行驶的距离为：

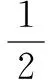
可得到两车的距离为x货-x警=36m

点拨运动学和力学中的临界值问题，比较常见的是追击和相遇问题，也就是讨论两物体运动的过程中，在相同的时间内达到的空间的位置，以例1为例，则存在两个关系，一个是时间关系，一个是位移关系，在做题的过程中，画草图也能够得到.在该问题中，临界条件则是两车的速度相等，也就是能否追的上的临界条件，也是判断分析的切入点.

二、竖直平面内的圆周运动的临界值问题

例2 如图1所示，将细绳为L，一端固定在O点，另一端系一质量为m的小球，如果使小球在恰好竖直平面内做圆周运动，，则小球到达最低点的速度是多少？

图1

分析小球在做圆周运动的时候，其临界最小的速度为mg=mv2/r,

解由物体做圆周运动的时候可知，当物体达到最低点的时候，因为向心力跟重力相等

点拨在小球做圆周运动的时候，在圆形轨道中，临界条件是一样的，只要求出小球在受力平衡的时候受力情况，则可以求出相应的临界值速度.同理，在圆运动的过程中，也可以换成轻杆，则这时候临界条件变为零.

三、电学中常见的临界值问题

例3 如图2所示，在一个水平向右的匀强电场中，场强未知，在选点O上挂有一绳长为l的细绳，下端系着质量为m，电量为+q小球，将小球拉到水平位置静止进行释放，当小球摆到C点的时候，再重新摆回.当OC与竖直方向成30°角，求小球在运动过程中的最大速度是多少？

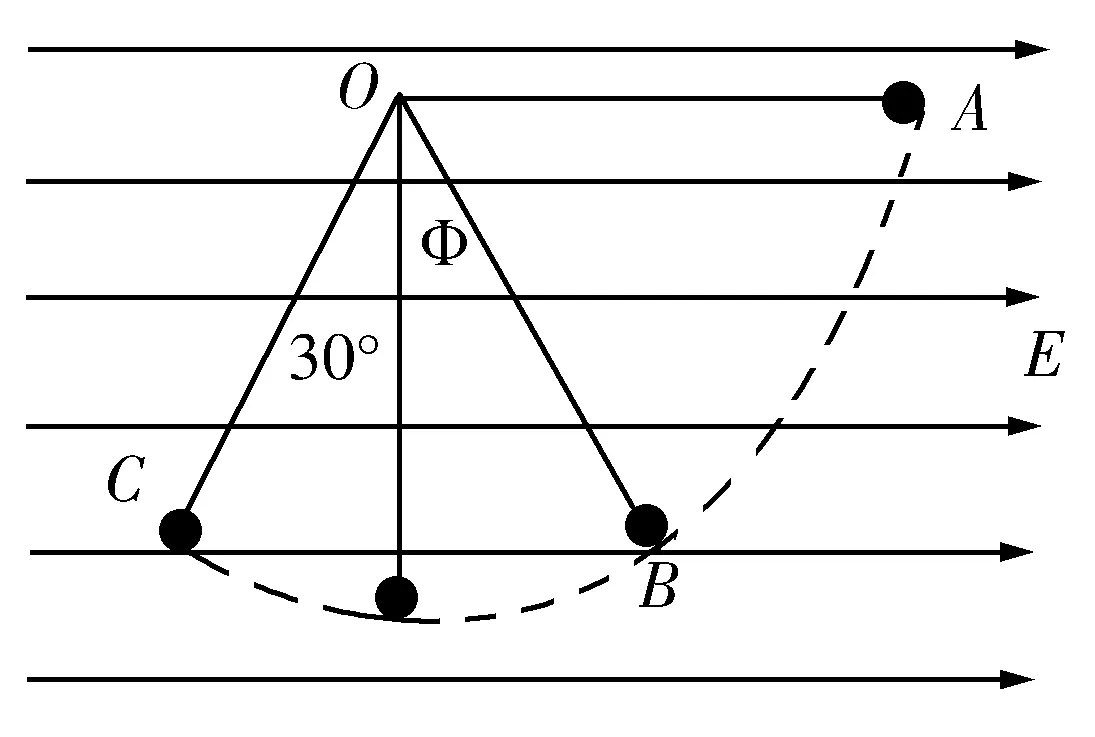
图2

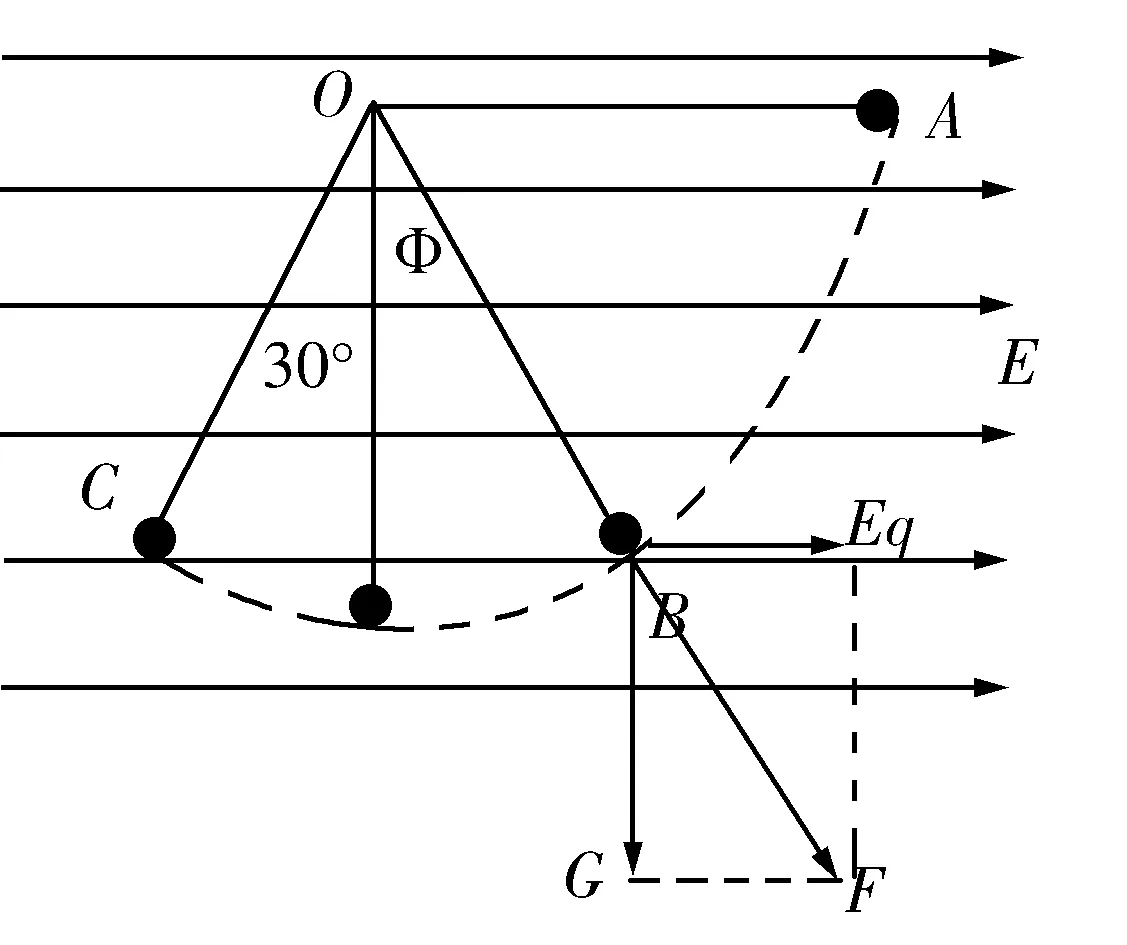
图3

分析在该电场中，小球从A到C的运动类似单摆运动，单摆的过程中，物体到达平衡位置的时候有最大速度，也就是当小球达到B点处于平衡，具有最大速度，这时候小球与竖直位置成φ=30°也或者是在小球运动的过程中，从A到C的运动，是在重力场和电场的复合作用下进行的，也就是在由这两种场力组成的复合场力与小球共线，为小球的平衡位置，这时候小球有最大速度.

则可以求出

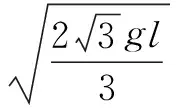
点拨在电场和重力场的综合场的作用下进行分析，则首先要能够找到其临界问题的临界条件，对临界条件中物体的受力进行分析.在该题的解题过程中，首先要能够意识到小球的运动类似单摆，找到单摆在静止的过程中受力情况则可以分析出小球的临界速度.

此外，在有关物体在质量守恒和带电粒子在有界磁场中的运用的过程中，牛顿运动定律的临界值的过程中也经常会遇到临界值的问题.这些问题的过程中主要是通过分析物体运动的过程中所处的临界状态和临界值，则可以以这个为突破口进行受力分析，使问题得以解决.

在临界值问题中，临界状态的判断和分析要能够与平衡态和极限思维练习在一起，在给定的物理情景中求物体物理量的最大值或者是最小值，跟高等数学中国的极限值思维是相似的，所以，在解答这一类题目的过程中，首先在脑海中有有清晰的物理情景，再进行物理过程的分析，根据物体的受力情况，找到相应的临界值条件或者是极值的条件，解决问题，这样也可以培养思维逻辑能力和分析能力.同时也要能够夯实课本上的主要公式和定理，这样可以熟练地运用所学知识，在分析的时候很快找到相应的思路.

[1]闻韬. 运用临界条件解决高中物理带电体在磁场中运动的问题[J]. 亚太教育,2016,(04).

[2]胡俊梅. 高中物理临界极值问题的处理方法[J]. 和田师范专科学校学报,2012,31(05).

G632

B

1008-0333(2017)22-0084-02

2017-06-01

孙瑞凝(2001.10-)，女，山东肥城，高中在读.

责任编辑：闫久毅]