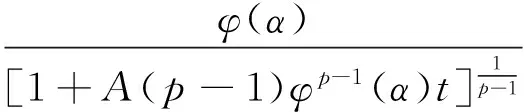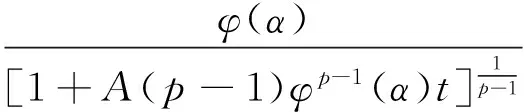贝努利型方程组初值问题的整体解
2017-10-20胡晶地
胡晶地
(浙江广厦建设职业技术学院 信息与控制工程学院, 浙江 东阳 322100)
贝努利型方程组初值问题的整体解
胡晶地
(浙江广厦建设职业技术学院 信息与控制工程学院, 浙江 东阳 322100)
常微分方程; 贝努利型方程组; 初值问题; 整体解
MSC2010:34A30
0 引 言
王高雄等在文献[1]中讨论了常微分方程初值问题
(1)
的积分曲线.其通解为:

(2)
由(2)式可知:
① 当A>0,B>0时,若y0<0,则解必在有限时刻趋于无穷大,若y0≥0,则解对一切t≥0存在;

定义1 若常微分方程初值问题的解对一切t≥0存在,则称其为常微分方程初值问题的整体解.
研究常微分方程初值问题的整体解[2-4],对常微分方程理论和拟线性双曲型方程柯西问题的整体解研究有重要意义[5-7].
下面研究一般的初值问题:
(3)
其通解为:

(4)
若a(t),b(t)∈c[0,+),y0b(t)<0,则由(4)式可知,通解中的分母对一切t≥0有意义,且恒不为零,于是对一切t≥0,(3)式的解均存在,即有唯一的整体解.这可表述为如下定理:
定理1 初值问题(3)式有唯一整体解的充分条件是:
①a(t),b(t)∈c[0,+);
②y0b(t)≤0.
定理1中的条件①起到使(3)式存在唯一局部解的作用,条件②对整体解的存在起决定性作用.
1 主要结论
定义2 形如
(5)
初值条件
(6)
的方程组称为贝努利型方程组.
命题初值问题(5)式、(6)式有唯一整体解的充分条件是:
①a1(t),a2(t),b1(t),b2(t)∈c[0,+);

证明由命题中的条件①知,a1(t),b1(t),a2(t),b2(t)∈c[0,+),所以(5)式的右端函数不但是t≥0半空间的t,x1,x2的连续函数,而且关于x1,x2满足李普希兹条件,根据常微分方程初值问题的局部解存在定理,存在t1>0,在[0,t1]上有唯一的局部解.这个局部解还可以向t的增加方向延拓,由于(5)式的右端函数定义在t≥0的半空间上,是一个无界区域,根据解的延拓定理可能出现两种情况:一种是解可一直延拓下去,直到t→+;一种是存在有限时刻t*>0,当t→t*时,x1(t),x2(t)中至少有一个趋于无穷大.前一种情形就是整体解.由此可见,为证明整体解的存在性,只需证明如下的定理:
定理2 对任意时刻0 下面用几个引理和证法来证明这个定理. 设方程组(5)式、(6)式的解经过延拓,已在[0,t*)上有定义,在这个区间上,x1(t),x2(t)是t的已知函数.在(5)式的第一式中可以将x1(t)看作未知函数,将a1(t)x2(t),b2(t)看作系数,这样它就是贝努利方程,解得: (7) 同理 (8) 引理1 若存在有限时刻t*>0,使x1(t*),x2(t*)中至少有一个取值无穷大,则 (i) 当t→t*时,x1(t),x2(t)同时趋于无穷大,且均趋于+; (9) (10) (11) 证明(i) 采用反证法.不失一般性,可设t→t*时,x1(t*)为有限.则由(8)式知,当t→t*时,x2(t*)也为有限,与引理条件矛盾.而且由(7)式、(8)式知,此时x1(t*),x2(t*)均取值+. (ii) 由(i)知,x1(t*)=+,x2(t*)=+.采用反证法.不失一般性,可设a2(t)x1(t)dt为有限或为-,则由(8)式得知x2(t*)为有限,与引理假设矛盾.而且不难看出a1(t*),a2(t*)均取正值. (iii) 证明略. (iv) 由(iii)知,当b1(t)b2(t)≠0时, (12) (13) 所以(11)式成立. 引理2 若存在有限时刻t*>0,使x1(t*),x2(t*)中至少有一个取值无穷大,则(11)式不能成立. 证明将积分曲线x1(t),x2(t)在t=t*处的斜率方程(5)式结合起来讨论,以期得到与(11)式矛盾的结果. 令 (14) 当t→t*时,方程组(5)式、(6)式解的积分曲线的斜率由(5)式和(14)式确定,分别为: (15) 由(i)知,当t→t*时,x1(t),x2(t)均趋于+,因而t=t*为它们的垂直渐近线,所以当t→t*时, 故由(15)式可知,必需 即 也即 (16) 由此可见,若(11)式成立,则(16)式不能成立. 作为应用,下面研究一阶拟线性方程的初值问题: (17) 其中λ(u)为u的一阶连续可导函数,且λu>0,A>0,p≥1,φ∈c1(R). 令 (18) 的解为: x=x(t,α),α=x(0,x), (19) 则(17)式可改写为: (20) 解得: (21) 显然,只要 A(p-1)φp-1(α)≥0, (22) (21)式对一切t≥0有意义. 为了得到(17)式的整体解,还必须估计ux,为此将(17)式关于x求导,得: (23) 由于λu,u均是t的已知函数,所以(23)式是贝努利方程的初值问题.由命题知,只要 (24) ux对一切t≥0有解,从而ut对一切t≥0有意义,故得: 定理3 初值问题(17)式有整体解的充分条件是(22)式、(24)式成立. (24)式等价于φ′(α)≥0.(19)式、(24)式还是初值问题(17)式有整体解的必要条件,证明略. [1] 王高雄,周之铭,朱思铭,等.常微分方程[M].北京:高等教育出版社,2008. [2] 王仲平.含有间断项的常微分方程初值问题解的存在唯一性[J].兰州交通大学学报(自然科学版),2004,23(1):124-128. [3] 汪璇.Banach空间常微分方程初值问题的广义整体解[J].西北师范大学学报(自然科学版),2003,39(4):9-12. [4] 罗环环,范胜君.常微分方程初值问题解的存在唯一性[J].吉林大学学报(理学版),2015,53(2):166-172. [5] 宋娈娈.拟线性双曲型方程组解的整体存在性[J].高师理科学刊,2014,34(6):1-6. [6] LI S M.Cauchy problem for general first order inhomogeneous quasilinear hyperbolic system[J].Journal of Partial Differential Equations,2002,15:46-68. [7] 李才中,肖玲.一类拟线性双曲型方程组的整体解[J].数学学报,1976,19(4):263-275. MSC2010:34A30 GlobalSolutionsofInitialValueProblemsforBernoulliTypeEquations HU Jingdi (Information and Control Engineering School, Guangsha College of Applied Construction Technology, Dongyang 322100, China) ordinary differential equation; Bernoulli type equations; initial value problem; global solutions 2017-06-10 胡晶地,教授,研究方向:微分方程.E-mail:hjd6637300@163.com O175.1 A 1009-1734(2017)08-0001-05 [责任编辑高俊娥]

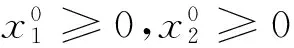


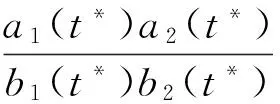



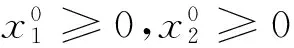
2 应用举例