基于任务分解的合成营作战编组规划模型*

郭 峰,王树坤， 孟凡凯

(陆军军官学院,安徽 合肥 230031)

基于任务分解的合成营作战编组规划模型*

郭 峰,王树坤， 孟凡凯

(陆军军官学院,安徽 合肥 230031)

针对陆军合成营作战任务分解得到的元任务,以合成营各类型作战单元用于执行元任务的数量规模为决策变量,以作战资源和合成营作战单元数量为约束条件,以兰彻斯特战争模型为基础推导出作战伤亡函数,并以伤亡最小为目标函数,为陆军合成营作战编组建立了规划模型,实现了动态编组。

任务分解; 合成营; 作战编组; 规划模型

王树坤(1962-),男,教授,硕士生导师。

孟凡凯(1981-)，男，博士，讲师。

合成营的作战编组始终是面向其所担负的作战任务的,本文在对陆军合成营的作战任务进行分解的基础上,将原本较为宏观的作战任务分解为若干可被合成营作战单元直接执行的元任务。通过分析元任务对作战资源的需求,将合成营各作战单元所具备的作战能力与之相匹配,通过建立规划模型来确定陆军合成营针对该任务的作战编组。

1 基于WBS的合成营任务分解

WBS(工作分解结构，Work Breakdown Structure)是项目管理过程中将项目以可交付成果为导向进行分组的过程。本文将WBS的思想运用于陆军合成营作战任务的分解,通过若干次分解,得到任务层次网络,其顶层为需要最终完成的作战任务,底层为可被直接执行的元任务层,中间层为子任务,如1图所示。

图1 任务分解示意图

1.1 陆军合成营作战任务分解原则

1)粒度原则

使命分解过程中,分解得到子任务,当子任务的执行需求与作战单元的能力矢量关联时即作为元任务而不再继续分解。

2)百分百原则

父层子任务内容必须是下一层子任务或元任务之和,并且分解得到的子任务要百分之百代表父层子任务。

3)同层同标准原则

同层同标准原则是指分解过程中,同一层次的子任务必须由同一种分解标准分解获得。

1.2 基于WBS的陆军合成营作战任务分解方法

1)按作战顺序进行分解：是指按照子任务执行的时间或逻辑顺序来进行分解。比如,在陆军合成营进行登陆作战时,可将任务按战斗进程分为装载上船、航渡、直前信火打击、展开、换乘、泛水、编波、抢滩上陆、扩大巩固登陆场、向敌纵深突击等。

2)按作战空间进行分解：是指按照陆军合成营完成子任务可能的空间分布来对任务进行分解。为便于数学表达,可建立坐标系,对整个战场区域进行划分。

3)按功能进行分解：是指按照陆军合成营所具有的功能进行分解。在本文中,按照功能分解的最小粒度设置为可被一类作战单元独立完成的子任务。

1.3 基于WBS的陆军合成营作战任务分解过程

在对陆军合成营作战任务进行分解的实际操作过程中,通常情况下只采用一种分解方法并不能达到分解目标,需要综合使用几种分解方法进行反复分解。对于陆军合成营所有的作战任务,均可按照以下流程进行分解:

Step1:将总的作战任务按照作战时序进行分解得到若干子任务;

Step2:将Step1分解得到的子任务分别用百分之百原则、同层同标准原则进行检验,若未通过检验,返回Step1重新分解;若通过检验,则进入检验判断其是否满足粒度原则,若满足,则得到元任务,分解结束。若不满足,则进入Step3;

Step3:将Step1分解得到的子任务按照作战空间进行分解得到下一层次的若干子任务;

Step4:将Step3分解得到的子任务分别用百分之百原则、同层同标准原则进行检验,若未通过检验,返回Step1重新分解;若通过检验,则检验其是否满足粒度原则,若满足,则得到元任务,分解结束。若不满足,则进入Step5;

Step5:将Step3分解得到的子任务按照作战功能进行分解得到下一层的若干子任务;

Step6:将Step5分解得到的子任务分别用百分之百原则、同层同标准原则、粒度原则进行检验,若未通过检验,返回Step1重新分解;若通过检验则得到元任务,分解结束。

图2即为分解过程流程图。

图2 基于WBS的合成营作战任务分解流程图

由于实际作战过程非常复杂,模拟实战过程的规划模型也将十分复杂,具体体现在:首先,元任务之间的时序关系并不是简单的串行或并行关系,而且完成时间皆不相同,即同一时间段内某些任务执行完毕,有些任务仍在执行,对模型构建造成了很大的困难;其次,作战过程中陆军合成营存在人员伤亡和装备损耗,即作战能力下降而直接影响随后的任务规划,而要模拟这一过程非常困难;再次,实际作战中合成营很可能会得到上级或友邻支援而作战能力倍增,这在建模过程中难以体现。

限于论文篇幅和个人能力,为了便于模型的建立,做以下假设:

假设一:所有元任务都被成功执行;

假设二:任一作战单元只有在当前任务执行完成后才会执行下一个任务;

假设三:任意时间点上,元任务对作战资源的需求小于作战单元所能提供的资源总和;

假设四:战场相对线性,所有执行某元任务的作战单元在任务开始前都能到达该任务区域;

假设五:每个元任务结束后,执行该任务的所有作战单元的损耗都得到补充。

2 合成营作战编组规划模型

2.1 决策变量

规划的主要目的是为了确定在作战过程中的任意时间点T,合成营作战单元Zi正在执行元任务MTj的数量qij,因此,应将qij作为决策变量。

2.2 约束条件

2.2.1 元任务作战资源最低需求约束

执行各元任务的作战单元数量所含作战资源之和不得少于元任务对作战资源的最低需求:

RZik·qij≥RMjk

(1)

式中，RZik为单个作战单元Zi包含作战资源Rek的数量;RMjk为元任务MTj对作战资源Rek的最低需求数量。

2.2.2 作战单元数量约束

在作战过程中,作战单元每完成相应的任务都会有不同程度的人员伤亡和装备损耗,即其作战能力会有相应程度的降低,包含的作战能力资源会有同样程度的减少。而不同作战任务对作战单元的损伤率是不同的,由于任务之间存在的逻辑时序关系比较复杂,若将完成每一元任务的损耗对之后的影响考虑在内将使模型十分复杂,为便于建模,假设每个元任务完成后的损耗都会被补充(即假设五)。

由于元任务的时序并非按顺序排列,同一时间段内有若干元任务在同时进行中,因此不能对作战全过程的资源占用情况进行规划,而应针对任意时间点的作战单元执行元任务的情况进行规划。

如图3所示,横坐标为作战时间T,纵坐标每一区间的宽度为各作战单元数量,图中各矩形代表各元任务,其长度代表元任务MTj的执行时间tj,起点为任务起始时间Tj,其宽度代表执行该元任务的作战单元数量。

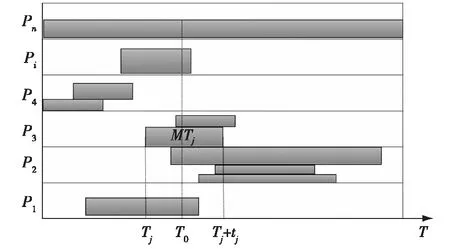
图3 作战单元执行元任务示意图

在任意时间点T0,进行中的元任务所占用的作战单元数量不能大于该类作战单元固有数量:

∑qi≤pi

(2)

式中，qi为在任意时间点正在执行某元任务的作战单元Zi的数量;pi为作战单元Zi的数量。

2.3 目标函数

随着战争形态的发展,人们对战争的态度和观念也在不断变化,现代战争中对人的生命的重视程度越来越高。各国争相发展新型无人化装备的出发点也是减少人员在战争中的伤亡。因此,本文也将伤亡最低作为规划模型的目标函数。

2.3.1 基于兰彻斯特战争模型的伤亡规模推导

兰彻斯特战争模型无疑是模拟战争最经典的模型,其典型模型包括平方律模型、线性律模型以及混合模型,分别适用于简化的正规战争、游击战争和战争一方为正规部队而另一方为游击部队。对于本文所研究的合成营作战问题,平方律模型较为适合,其基本模型为

(3)

式(3)中的x、y分别表示敌、我双方的作战力量规模,a、b称为毁伤系数,a表示单位时间内我方单个作战个体对敌方的毁伤数量;b表示单位时间内敌方单个作战个体对我方的毁伤数量。

由式(3)可得

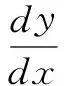
(4)

求解得

ay2-bx2=k

(5)

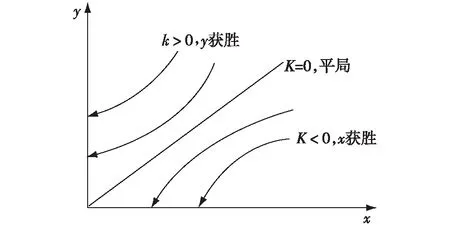
图4 兰彻斯特平方律模型相轨线

假设最后我方获胜,即k>0。当作战结束时,我方剩余兵力为

(6)

我方伤亡人数ys为

(7)

式(3)为单一兵种兰彻斯特方程组,在此基础上,多兵种作战的兰彻斯特方程为

(8)

式(8)中,aji表示敌方第j种兵种对我方第i类兵种的毁伤系数,xji为敌方第j类兵种参与对我方第i类兵种作战的规模,同理,yij表示我方第i类兵种参与对敌方第j类兵种作战的规模。假设战争结束时我方获胜,则我方伤亡总数为

ys=∑∑(yij0-yij(t1))

(9)

2.3.2 陆军合成营作战伤亡规模函数

将式(9)运用于合成营完成作战任务时作战伤亡情况,则aij对应元任务MTj对作战单元Zi的毁伤系数,bji对应作战单元Zi对元任务MTj的毁伤系数;yji0对应执行元任务MTj的作战单元Zi的数量qij,xji0对应元任务MTj中敌方兵力初始规模。在有假设五的条件下,陆军合成营完成所有元任务后的伤亡数量为

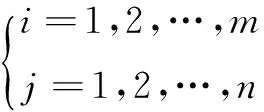
(10)

式中，Qs为完成任务后合成营总的伤亡数量;m为作战单元类型数量;n为元任务数量。Qij(t)为合成营作战单元Zi执行元任务MTj时作战力量规模随时间变化的函数;ωj为元任务MTj内敌方初始兵力,其数值对于所有作战单元Zi均一致。

2.4 编组规划模型

综合以上建模过程,可以得到以作战单元Zi执行元任务MTj的数量qij为决策变量,以伤亡最小为目标函数的陆军合成营作战编组的规划模型为

s·tRZik·qij≥RMjk

∑qi≤pi(在任意时间点)。

3 结束语

本文在对合成营作战任务分解的基础上,通过建立规划模型,实现了对陆军合成营作战的动态编组,即编组随任务的变化而实时变化,与传统作战编组相比具有更好的任务适用性和自组织性。

[1] 胡浩然,朱皖松，王俊,等.基于合同作战的兰彻斯特方程[J].四川兵工学报,2010(8):126-127.

[2] 占栋辉，陈刚，张宏军，等.现代化条件下的兰切斯特战斗模型[J].计算机工程与应用，2013，49(15)：246-248.

[3] 杨世幸,阳东升，刘忠,等.作战使命分解与任务建模方法[J].火力与指挥控制,2009，34(8):24-29.

[4] 阳东升,张维明,等.战役任务计划的数学描述与求解算法研究[J].系统工程理论与实践,2006，26(1):26-34.

Mission Planning Model of Synthetic Battalion’s Combat Formation Based on Task Breakdown

GUO Feng,WANG Shu-kun

(Army Officer Academy,Hefei 230031,China)

Found a planning model based on the task unit by decomposing the mission of the army synthetic battalion,with the decision variable of each unit of synthetic battalion’s scale to execute the task unit,and the constrain condition of quantity of the operational resources and the synthetic battalion’s combat unit,and the objective function of minimum injuries and deaths inferred by Lanchester equation.Dynamic formation has been achieved.

task breakdown; synthetic battalion; combat formation; mission planning model

E83

A

10.3969/j.issn.1673-3819.2017.05.004

1673-3819(2017)05-0018-04

2017-06-27

2017-07-15

2016年全军军事学研究生课题(2016JY135)

郭 峰(1988-),男,江苏海门人,硕士研究生,助教,研究方向为战术学。