助推滑翔高超声速反舰导弹突防密集阵武器能力分析

王少平,董受全,李晓阳,张华英

(1.海军大连舰艇学院,辽宁 大连 116018;2.92956部队,辽宁 大连 116041)

助推滑翔高超声速反舰导弹突防密集阵武器能力分析

王少平1,董受全1,李晓阳2,张华英1

(1.海军大连舰艇学院,辽宁 大连 116018;2.92956部队,辽宁 大连 116041)

在分析对比助推滑翔高超声速反舰导弹与传统反舰导弹在飞行弹道等方面差异的基础上,建立下压段导弹质心运动方程以及目标运动模型,并以满足落角约束的最优导引律作为下压段的导引律,对助推滑翔高超声速反舰导弹的飞行弹道进行仿真分析;建立密集阵武器系统与助推滑翔高超声速反舰导弹的攻防对抗仿真模型,使用蒙特卡罗法仿真计算导弹飞行速度、落地倾角等对反舰导弹突防概率的影响。通过仿真分析得出了助推滑翔高超声速反舰导弹突防密集阵武器系统的能力,为助推滑翔导弹的作战使用提供理论支撑。

高超声速;反舰导弹;密集阵系统;突防能力

董受全(1968-),男,博士,教授。

李晓阳(1985-),男,硕士,助理工程师。

张华英(1990),男,硕士。

近年来,随着高超声速动力技术、热防护技术、气动力设计等快速发展,包括助推滑翔高超声速导弹在内的各种高超声速武器也得到了巨大的发展和进步。从目前各国在高超声速巡航导弹和助推滑翔高超声速导弹的研究和试验情况来看,助推滑翔高超声速导弹以技术难度较低等优势可能使其会成为第一型投入使用的高超声速导弹武器。

助推滑翔高超声速导弹与高超声速巡航导弹以及其他超声速和亚声速战术导弹相比,具有飞行速度快、弹道变化大等特点,这些特点都对其突防能力有一定影响。而密集阵武器系统是包括美国在内的诸多国家水面舰艇末端防御的一个重要组成部分,以往对密集阵拦截反舰导弹的研究文献有很多,覆盖了亚声速、超声速和高超声速导弹。例如文献[1-2]对密集阵拦截高超声速导弹的有效性及方法进行了研究。这些文献在研究过程中得出了很多结论,但以往文献在研究密集阵的攻防过程中,基本的假设条件都是反舰导弹进行匀速运动,这对以往的传统反舰导弹来说,由于其有持续的动力,在整个飞行过程中速度变化不大,因此这一假设条件是合理的,但对助推滑翔高超声速反舰导弹来说,由于其在下压段时导弹并无动力,导弹在气动阻力的作用下飞行速度逐渐减小,且助推滑翔高超声速导弹下压段一般有落地倾角约束,因此其弹道是在不断变化的,这与文献[1-2]将高超声速导弹下压段弹道看作直线是不一致的,而这将直接影响最终的研究结论。基于此,对密集阵拦截助推滑翔高超声速反舰导弹进行研究。

1 助推滑翔导弹下压段弹道模型

由于密集阵为末端防御系统,其只可对处于下压段末端的助推滑翔高超声速反舰导弹进行拦截,因此后续仅对下压段的弹道进行分析。

1.1 质心运动方程

由于高超声速反舰导弹在下压段飞行距离较小,因此可忽略地球自转的影响,认为其在下压段仅受空气动力和地球引力的作用。同时,由于助推-滑翔导弹在下压段一般采用BTT控制方式,因此导弹在飞行过程中侧滑角可近似为零[3]。此外,由于反舰导弹打击的目标为水面舰艇类运动目标,因此当以目标坐标系为参考时,可将目标机动速度矢量叠加至导弹运动速度矢量上,则导弹质心运动的动力学标量方程和运动学方程[4-5]可表示为:

(1)

(2)

式中,m为导弹质量;V为导弹飞行速度;θ为导弹的速度倾角;σ为导弹的速度偏角;ν为倾侧角;g为重力加速度;Sref为导弹参考面积;CL为导弹升力系数;CD为导弹阻力系数;ρ为大气密度;(x,y,z)为导弹在目标坐标系中的坐标;L为导弹气动升力,L=0.5ρV2CLSref;D为导弹气动阻力,D=0.5ρV2CDSref。

1.2 导引规律

为使助推滑翔高超声速导弹下压段命中目标时对目标形成较大毁伤,一般对导弹在下压段的落地倾角有要求,在此选择再入机动弹头常用的一种满足落角约束的最优导引律,该导引律按照俯仰平面和转弯平面进行独立设计,在俯仰平面和转弯平面的导引方程分别为[6-7]

(3)

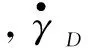
1.3 目标机动模型

由于反舰导弹主要打击的对象为水面舰艇类目标,属于机动目标,因此需要对水面舰艇的机动方式进行模拟。水面舰艇的实际机动方式比较复杂,不仅要受到舰艇本身性能的影响,同时要受到海区环境等的影响,为简化问题,认为反舰导弹末制导雷达开机后目标水面舰艇的机动速度始终保持不变,并且水面舰艇机动样式主要为三种,即直线机动、一次转弯机动和连续转弯机动,如图1所示。并且假设水面舰艇在转弯过程中始终是以某一中心点,且以固定的转弯角速度进行转弯。由于密集阵系统持续射击时间只有几秒,因此认为在此过程中目标的航向始终不变,即采取直线机动。

图1 水面舰艇机动样式

2 密集阵拦截模型

由于密集阵作为末端防御武器,在其采取抗击行动前,已有舰空导弹进行了抗击,因此可认为密集阵搜索雷达可在最远搜索距离上有效发现和捕获来袭反舰导弹,仅对以下几个密集阵系统射击行动涉及的主要问题进行分析。

2.1 导弹受弹面积模型

首先建立密集阵拦截坐标系。定义密集阵拦截坐标系Ocxcyczc的原点Oc位于密集阵系统的质心位置,xc轴取舰艇运动方向,zc轴垂直水平面向上,yc轴根据右手定则确定。在此基础上定义导弹二维受弹面坐标系Osxszs,定义其原点Os位于反舰导弹与密集阵弹丸遭遇时刻导弹的质心点位置,xs轴和zs轴分别指向方位角脱靶方向和高低角脱靶方向,如图2所示。图2中M为导弹位置点,T为水面舰艇的质心点位置。

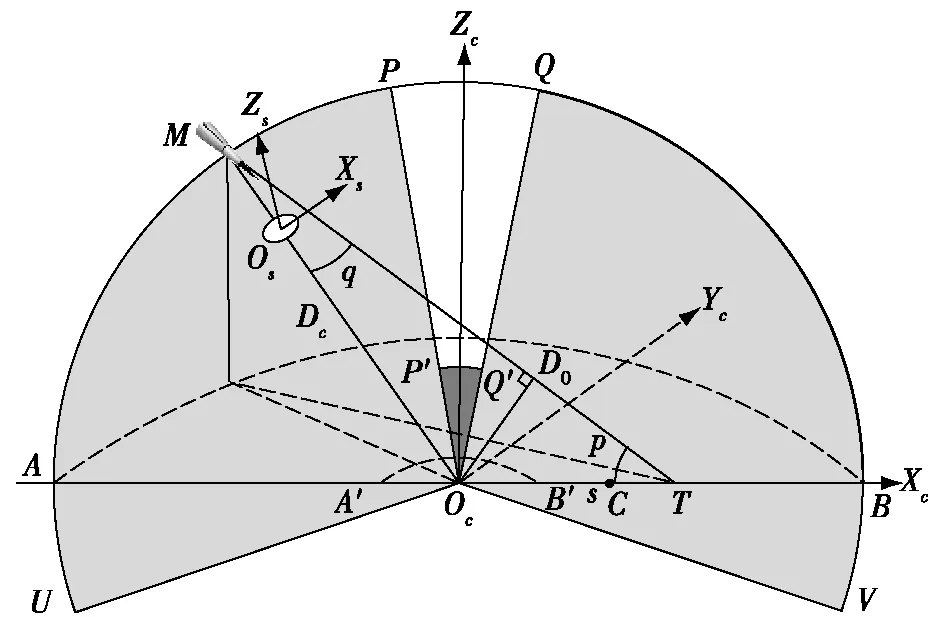
图2 密集阵防空作战态势图

图2是密集阵系统与导弹攻防对抗的静态态势,实际上这一对抗过程是始终变化的。如图3所示,假设t=0时,密集阵系统的质心点为O0,舰艇的质心点为T0,导弹与密集阵首次遭遇时导弹的入射角和反舰导弹与密集阵弹丸的遭遇角分别为p0和q0,导弹的质心点为M0,此时弹目距离为DT0。则经过时间Δt密集阵系统的质心点为O1,舰艇的质心点为T1,导弹与密集阵首次遭遇时导弹的入射角和反舰导弹与密集阵弹丸的遭遇角分别为p1和q1,导弹的质心点为M1,此时弹目距离为DT1。

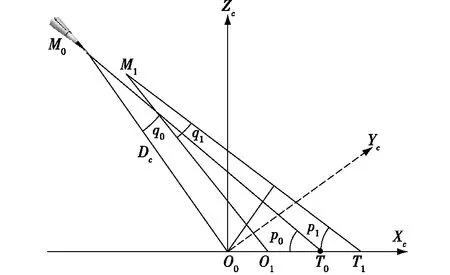
图3 密集阵攻防动态变化图

由于导弹在飞行过程中,弹目距离DTi与pi是一一对应的,且已知密集阵系统质心点至舰艇质心点的距离s,因此,依据几何关系可得任一时刻导弹与密集阵质心间的距离Dci,即

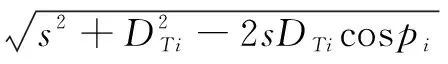
(4)

当Dci=Dc,max时,此时是密集阵弹丸与导弹首次遭遇的距离,将此时的参数DTi与pi和Dci分别记为DT0、p0、Dc0。

根据三角几何关系得出:

(5)

当经过时间Δt后,密集阵质心点距导弹的距离为:

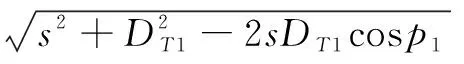
(6)

则

(7)

以此类推,可得任意ti时刻的遭遇角qi,即

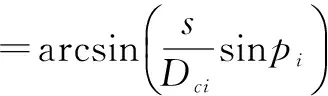
(8)

根据文献[8]等的假设,可将任意时刻ti导弹在受弹面坐标系上的投影面积可表示为

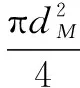
(9)

式中，dm为导弹的直径,lm为导弹的长度,hm为lm的投影长度。

为计算方便,且由于助推滑翔高超声速反舰导弹末端落地倾角较大,则qi很小,因此可将导弹受弹面积简化为圆形,圆形半径为

(10)

在受弹面积简化的基础上,假设第i枚弹丸的飞行距离为Li,则在受弹面坐标系上,第i枚弹丸的坐标为(Litanγi,Litanφi),则该枚弹丸是否命中根据下式判断[1]:

(11)

则在一次连续射击下,导弹总的受弹数为

(12)

式中，Na为密集阵系统在最大持续射击时间ta内发射的弹丸总数。

2.2 发射区及可持续射击时间模型

由于密集阵弹丸的速度在飞行过程中会随时间逐渐衰减,由于弹丸的飞行时间较短,因此可假设速度的衰减规律呈线性变化,则弹丸任意时刻的速度vc(t)为

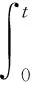
(13)

式中，vc0为弹丸初始速度;kc为弹丸速度衰减率;t为弹丸飞行时间。

理论上密集阵发射区的远界dc·max为密集阵首次开火射击与目标导弹间的距离,其与密集阵的最大有效射程Dc·max、弹丸在最大有效射程内的飞行时间tc·max和导弹的飞行速度vm有关,其数学关系为

(14)

密集阵发射区的近界dc·min为密集阵停火时位置点与目标导弹间的距离,其与密集阵的最小有效射程Dc·min、弹丸在最小有效射程内的飞行时间tc·min和导弹的飞行速度vm有关,其数学关系为

(15)

式中，Δt为采样周期。则密集阵最大可持续射击时间ta可由下式得出:

(16)

要求解上式,关键是确定vmi。由于反舰导弹的飞行弹道已知,理想条件下当密集阵首发弹丸经过时间tc,max与导弹遭遇,而在密集阵弹丸发射后,导弹经历飞行时间tc,max才与弹丸相遇,因此,导弹自首次遭遇密集阵弹丸到命中目标舰艇总的飞行时间为tc,max加上导弹飞行DT0所需的时间,由于已知导弹命中目标时刻的导弹速度,因此根据时间序列逆推就可得出密集阵首次发射时刻导弹的飞行速度vm0,进而可确定密集阵发射后任意时刻导弹的飞行速度vmi。求出导弹的飞行速度vmi后可通过迭代得出密集阵最大可持续射击时间ta。

2.3 平均必须命中数模型

按照文献[9]等对反舰导弹致命部位和非致命部位的划分标准,对于助推滑翔高超声速反舰导弹,一般将导弹的自动驾驶仪(控制)舱、引信和尾舱定义为致命部位,而将导引头、战斗部定义为非致命部位。

假设反舰导弹致命部位的长度为lmz,则任意时刻ti导弹致命部位的面积为

(17)

则此时平均必须命中弹丸数为

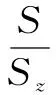
(18)

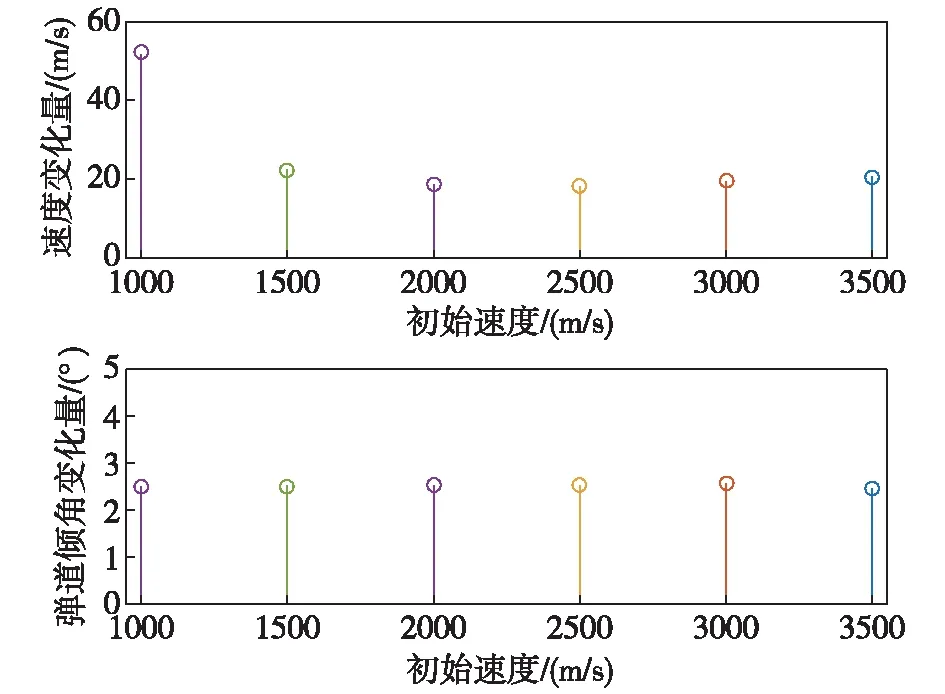
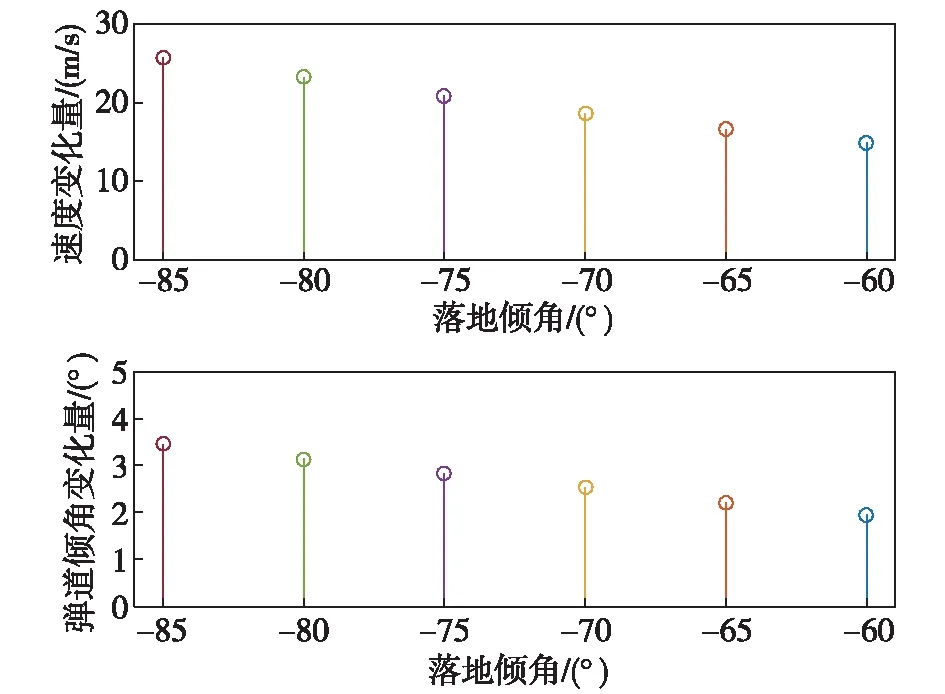
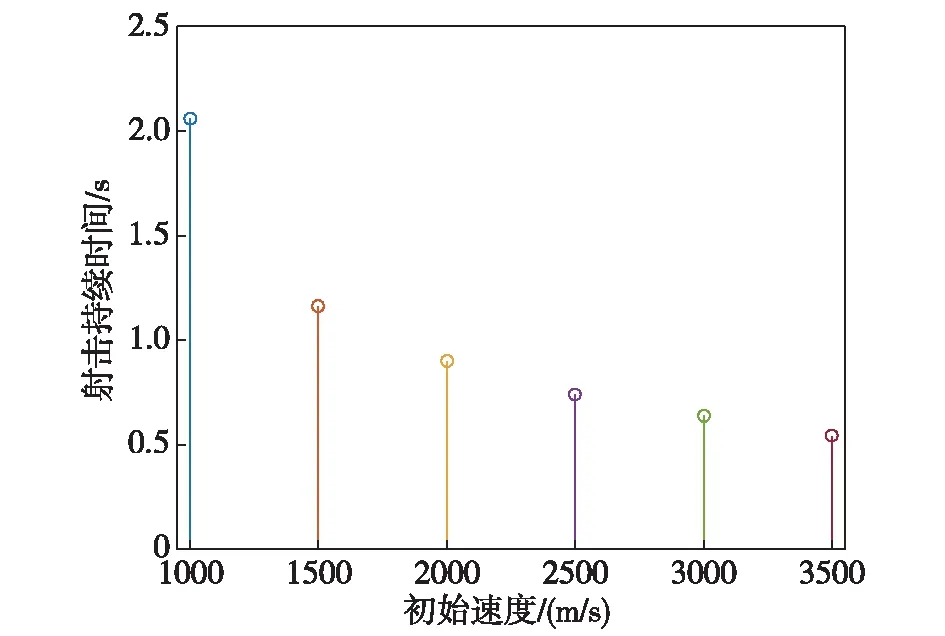
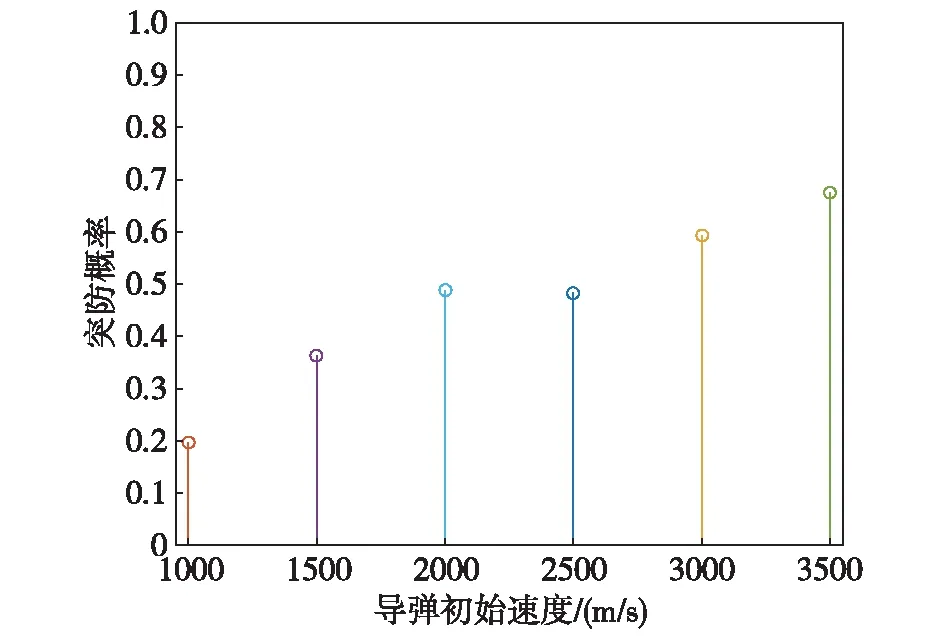
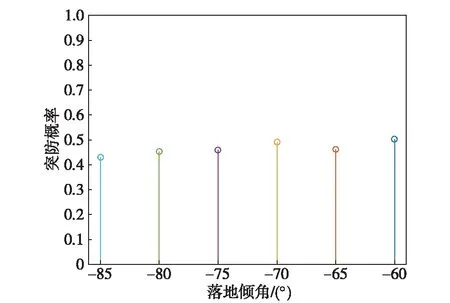
当密集阵对导弹进行一次持续射击后,如果命中弹数N≥Nb,则认为密集阵抗击成功,否则当N

当水面舰艇上有多个密集阵系统可对同一目标进行射击时,则逐一对单个密集阵系统的射击效果进行分析,最后综合多个密集阵的射击效果,即对每个密集阵系统射击命中弹数进行相加,则得出最终的命中弹数。

2.4 射击误差模型

密集阵系统的射击系统误差主要与跟踪精度、火力系统精度、火控系统精度有关,随机误差主要指弹丸散布误差。假设跟踪误差为e1(γ1,φ1),火力系统误差为e2(γ2,φ2),火控系统精度误差为e3(γ3,φ3),弹丸散布误差为e4(γ4,φ4),由于密集阵系统在对空射击时,一般认为弹着点散布在平面上,且散布服从二维正态分布,则密集阵系统的散布误差e(γ,φ)可表示为

(19)

则抽样算法可表示为

(20)

式中，u1～u4为标准正态分布随机数。

3 仿真及分析

根据上述模型,对助推滑翔高超声速反舰导弹与密集阵的攻防对抗进行仿真。仿真中定义目标航向是以导弹来向作为参考,顺时针为正。

3.1 基本仿真条件

1)导弹气动模型:采用文献[10]中CAV-H的气动数据,质量为907kg,气动参考面积为0.48378m2。

2)大气密度模型、声速计算模型、重力加速度计算模型采用文献[11]中的模型。

3)导引系数KD1、KD2、KT按照文献[7]分别取-4、-2和3。

4)密集阵参数如表1所示,其中最大有效射程取1470m。

表1 密集阵MK-15Block1B近防炮[12～15]

5)反舰导弹下压段初始条件:弹目距离100km,弹道倾角0°,弹道偏角0°,末制导雷达开机点高度为30km。

6)仿真条件:仿真步长为0.02,突防概率仿真中仿真次数取10000次。

3.2 密集阵拦截区内导弹弹道特性仿真

本文主要对助推滑翔高超声速反舰导弹在下压段密集阵拦截区内导弹的速度变化及弹道倾角变化情况进行分析,这里的拦截区是指密集阵系统的最大有效射程和最小有效射程范围内的区域。

1)导弹初始速度对其速度、弹道倾角变化量的影响

导弹初始速度分别取3500 m/s、3000m/s、2500m/s、2000m/s、1500m/s、1000m/s,落地倾角约束为-70°,目标处于静止状态,则导弹在密集阵有效射程范围内的速度变化量和弹道倾角变化量如图4所示。

图4 导弹初始速度对导弹速度、弹道倾角变化量的影响

2)导弹落地倾角对其速度和弹道倾角变化量的影响

初始飞行速度为2000m/s,落地倾角约束分别取-60°、-65°、-70°、-75°、-80°、-85°,目标处于静止状态,则导弹在密集阵有效射程范围内的速度变化量和弹道倾角变化量如图5所示。

图5 导弹落地倾角对导弹速度、弹道倾角变化量的影响

3)目标速度对导弹速度和弹道倾角变化量的影响

导弹初始飞行速度为2000m/s,落地倾角约束为-70°,目标速度分别取0、5kn、10kn、15kn、20kn、25kn、30kn,目标航向取0°,则导弹在密集阵有效射程范围内的速度变化量和弹道倾角变化量如图6所示。

图6 目标速度对导弹速度、弹道倾角变化量的影响

4)目标航向对导弹速度、弹道倾角变化量的影响

导弹初始飞行速度为2000m/s,落地倾角约束为-70°,目标航向分别取10°、30°、50°、70°、90°,目标机动速度取20kn,则导弹在密集阵有效射程范围内的速度变化量和弹道倾角变化量如图7所示。

图7 目标航向对导弹速度、弹道倾角变化量的影响

3.3 导弹持续射击时间仿真

1)导弹初始速度对密集阵持续射击时间的影响

导弹初始速度分别取3500 m/s、3000m/s、2500m/s、2000m/s、1500m/s、1000m/s,落地倾角约束为-70°,目标处于静止状态,则导弹初始速度对密集阵持续射击时间的影响如图8所示。

图8 导弹初始速度对射击持续时间的影响

2)导弹落地倾角对密集阵持续射击时间的影响

导弹初始飞行速度为2000m/s,落地倾角约束分别取-60°、-65°、-70°、-75°、-80°、-85°,目标处于静止状态,则导弹落地倾角对密集阵持续射击时间的影响如图9所示。

图9 导弹落地倾角对射击持续时间的影响

3)目标速度对密集阵持续射击时间的影响

导弹初始飞行速度为2000m/s,落地倾角约束为-70°,目标速度分别取5kn、10kn、15kn、20kn、25kn、30kn,目标航向取0°,则目标机动速度对密集阵持续射击时间的影响如图10所示。

图10 目标机动速度对射击持续时间的影响

4)目标航向对密集阵持续射击时间的影响

导弹初始飞行速度为2000m/s,落地倾角约束为-70°,目标航向分别取10°、30°、50°、70°、90°,目标机动速度取20kn,则目标航向对密集阵持续射击时间的影响如图11所示。

图11 目标机动航向对射击持续时间的影响

3.4 导弹突防概率仿真

假设导弹长度为5.21m,导弹直径为0.35m,致命部位的长度为1m。

1)导弹初始速度对导弹突防概率的影响

仿真初始速度分别为:3500m/s、3000m/s、2500m/s、2000m/s、1500m/s、1000m/s,落地倾角约束为-70°,目标处于静止状态,则导弹初始飞行速度对导弹突防概率的影响如图12所示。

图12 导弹初始速度对突防概率的影响

2)导弹落地倾角对导弹突防概率的影响

初始飞行速度为2000m/s,落地倾角约束分别为:-60°、-65°、-70°、-75°、-80°、-85°,目标处于静止状态,则导弹落地倾角对导弹突防概率的影响如图13所示。

图13 落地倾角对突防概率的影响

3.5 仿真结果分析

1)由图4得出在:导弹拦截区内,当助推滑翔高超声速反舰导弹下压段的起始速度在1000m/s～2500m/s内时,导弹起始速度越大,导弹在拦截区内的速度变化量越小;而当速度大于2500m/s时,起始速度越大,导弹在拦截区内的速度变化量越大,但变化幅度较小,例如起始速度为1000m/s时,速度变化量为52.37m/s,而当起始速度为2500m/s时,速度变化量为18.29m/s,当起始速度为3500m/s时,速度变化量为20.65m/s。此外当初始速度变化时,导弹在拦截区内的弹道倾角变化量约为2.5°,起始速度的影响不大。

2)由图5得:出在导弹拦截区内,导弹的落地倾角绝对值越大,速度变化量和弹道倾角变化量越小,落地倾角为-85°时速度和弹道倾角变化量分别为25.72m/s、3.45°。

3)由图6～图7得出:在导弹拦截区内,目标机动速度越大时,导弹的速度和弹道倾角变化量随目标机动速度的增大而增大,但增大幅度较小;当目标的航向越趋向导弹正横方向,导弹的速度和弹道倾角变化量逐渐减小,但减小幅度较小。

4)由图8得出:在导弹拦截区内,当导弹初始飞行速度越大,密集阵系统的持续拦截时间越小,如当导弹初始飞行速度为1000m/s时,密集阵持续射击时间为2.06s,当导弹初始飞行速度为3500m/s时,密集阵持续射击时间为0.54s。

5)由图9得出:在导弹拦截区内,当导弹落地倾角绝对值越小时,密集阵系统的持续射击时间越小,例如当落地倾角为-85°时,密集阵持续射击时间为1.02s,当落地倾角为-60°时,密集阵持续射击时间为0.84s。

6)由图10～图11得出:在导弹拦截区内,目标的机动队密集阵的持续射击时间影响较小,因此可以忽略目标机动速度和航向的变化。

7)由图12得出:导弹的初始速度对导弹突防概率影响很大,这主要是因为导弹的初始速度大,则在拦截区内留给密集阵的拦截时间极其有限,因此导弹的突防概率较大,例如当导弹初始速度为3500m/s时,突防概率为0.67,当初始速度为1000m/s时,突防概率为0.19。

8)由图13得出:导弹落地倾角绝对值越大时,导弹的突防概率总体是减小的,这主要是在初始弹道倾角固定的情况,为满足落地倾角约束,导弹要进行一定的机动,进而使导弹进入密集阵拦截区内时导弹速度较小,则密集阵有更多的时间对导弹进行拦截。

4 结束语

随着助推滑翔高超声速飞行器的武器化进程不断加快,助推滑翔高超声速反舰导弹未来极有可能出现在海战场上,而其在未来必然会成为各类传统防空武器和新型武器装备的拦截对抗目标。由于助推滑翔高超声速反舰导弹与传统反舰导弹在飞行弹道和速度等方面存在的巨大差异,其突防传统防空武器的能力究竟如何目前还需要进一步深入研究。同时,助推滑翔高超声速导弹突防新型防空武器的能力也是需要根据攻防双方武器准备的发展进行动态跟踪和研究的。针对这些问题,文中结合助推滑翔高超声速反舰导弹下压段的飞行弹道特点,给出了反舰导弹与密集阵系统的攻防对抗模型,该模型可较为准确地仿真助推滑翔高超声速反舰导弹突防密集阵过程,可为进一步研究助推滑翔高超声速反舰导突防能力提供理论依据。

[1] 张龙杰,谢晓方.密集阵武器拦截高超音速导弹有效性分析[J].弹道学报.2012,24(4): 37-41.

[2] 张龙杰,谢晓方,孙涛,等.密集阵对高超音速导弹的多点瞄准拦阻模型[J].弹道学报.2013,25(4): 15-20.

[3] 王少平,董受全,李晓阳,等.助推滑翔高超声速反舰导弹多方向协同突防可行性研究[J].指挥控制与仿真.2017,39(2): 55-60.

[4] 翁雪花.考虑终端约束的末制导方法研究[D].哈尔滨: 哈尔滨工业大学,2015.

[5] 卢晓东,郭建国,林鹏,等.导弹制导控制系统设计与Matlab仿真[M].西安:西北工业大学出版社,2010.

[6] 刘欣.助推-滑翔式飞行器弹道设计与制导技术研究[D].长沙:国防科学技术大学,2012.

[7] 张毅,肖龙旭,王顺宏.弹道导弹弹道学[M].长沙:国防科学技术大学出版社,2005.

[8] 宋贵宝,孔丽,李红亮,等.密集阵反导系统拦截反舰导弹模型研究[J].系统仿真学报.2004,16(10): 2128-2130.

[9] 王庆江,高晓光.反舰导弹未端机动突防“密集阵”系统的模型与仿真[J].系统仿真学报.2008,20(6): 1390-1393.

[10] 吕瑞.高超声速滑翔导弹滑翔段制导方法研究[D].哈尔滨:哈尔滨工业大学,2012.

[11] 刘燕斌.高超声速飞行器建模及其先进飞行控制机理的研究[D].南京: 南京航空航天大学,2007.

[12] 赵季阳.反舰导弹体系攻防对抗的仿真研究[D].太原:中北大学,2014.

[13] 糜玉林,鲁华杰,孙媛,等.基于VR-forces的“密集阵”火炮反导模型研究[J].舰船电子工程.2012,32(6): 76-79.

[14] 糜玉林,鲁华杰,孙媛,等.反舰导弹未端机动突防“密集阵”系统的模型与仿真[J].系统仿真学报.2008,20(6): 1390-1393.

[15] 孔寒雪.反舰导弹攻防对抗技术研究[D].北京:北京理工大学,2016.

Analysis of the Ability of Boost-glide Hypersonic Anti-ship Missile Breaking the Defense of Phalanx System

WANG Shao-ping1,DONG Shou-quan1,LI Xiao-yang2,ZHANG Hua-ying1

(1.Dalian Navy Academy,Dalian 116018; 2.Unit 92956 of PLA,Dalian 116041,China)

On the basis of analyzing and comparing the ballistic trajectory difference between boost-glide hypersonic anti-ship missile and traditional anti-ship missile,point-mass equation for missiles and target maneuver models are built,which are founded on the optimum guidance law with a terminal angular constraint of the dive phase,simulation analysis of the ballistic trajectory of boost-glide hypersonic anti-ship missile is conducted.Then engagement simulation models are built that between boost-glide hypersonic anti-ship missile and phalanx system.The penetration probability of boost-glide hypersonic anti-ship missile is simulated by the method of Monte-Carlo,which is influenced by vehicle and path angle.The ability of boost-glide hypersonic anti-ship missile breaking the defense of phalanx system is got,which is providing theoretical support for operational use of boost-glide hypersonic anti-ship missile.

hypersonic; anti-ship missile; phalanx system; penetration ability

E927;TJ761.14

A

10.3969/j.issn.1673-3819.2017.05.007

1673-3819(2017)05-0030-07

2017-05-25

2017-06-14

王少平(1985-),男,陕西洛南人,博士研究生,研究方向为反舰导弹作战使用。