车辆稳定性控制系统基于Simulink的仿真
2017-10-18刘波
刘波
(四川交通职业技术学院,四川成都610030)
车辆稳定性控制系统基于Simulink的仿真
刘波
(四川交通职业技术学院,四川成都610030)
稳定性控制系统是一种汽车主动安全技术,文章在Matlab/Simulink平台上,建立线性二自由度车辆模型,采用直接横摆力矩控制方法,选取质心侧偏角和横摆角速度作为稳定性控制系统的主控变量,设计了三种具有针对性的基于滑模变结构理论的车辆操纵稳定性控制策略。对三种稳定性控制策略的具体应用进行仿真分析,验证了所设计稳定性控制算法的有效性和鲁棒性。
稳定性控制;滑模变结构;有效性;鲁棒性
车辆稳定性控制系统通过抑制汽车过多和严重不足转向趋势,提高汽车的操纵稳定性。电气控制在提高汽车操纵稳定性和安全性方面的优势,使其成为汽车技术全面进步的推手。文章选取微型车为原型,进行结构化的改进,研究为避免汽车在行驶过程中可能发生的失稳现象而进行的稳定性控制。选取质心侧偏角和横摆角速度为主要控制变量并推导出三种具有针对性的控制策略,提出一种基于变结构滑模理论的横摆力矩直接控制的稳定性控制算法。通过车辆系统的建模、理论分析、控制算法研究、控制系统的建模与仿真分析,对在不同路况及不同前轮转角输入下的稳定性控制系统进行控制效果的比较分析,验证了控制算法的有效性。
1 车辆模型建立
如图所示,将整车简化成一个二自由度模型,整个车身可视为一个整体。二自由度分别是车辆沿y轴的侧向运动和绕z轴的横摆运动,且车辆沿x轴的纵向速度u视为不变。
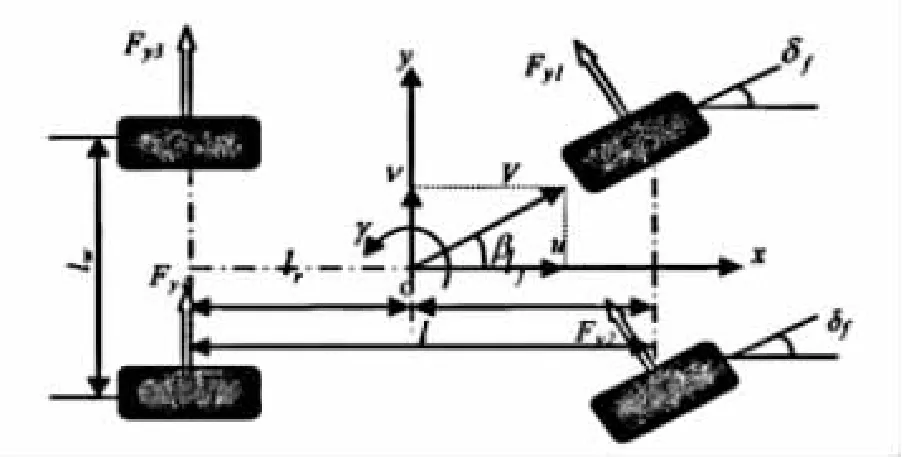
图1 车辆二自由度模型
β为质心侧偏角;γ为车辆的横摆角速度;δf为前轮转角;Fyi为轮胎侧向力;lf、lr为车辆重心至前后轴的距离;l为车辆的轴距;lw为轮距;μ、v为车体在固定坐标系下的纵向、侧向车速。
在每个车轮上的垂直载荷FZi(i=1~4)由车辆重量和在加速度作用下的载荷转移组成。各个车轮的垂直载荷可表示为:
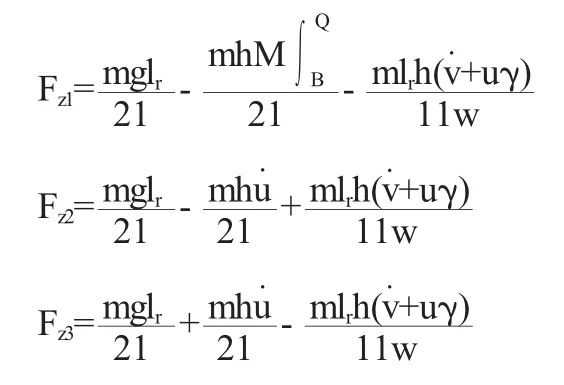

当不考虑轮胎的非线性特性,忽略左、右车轮垂直载荷的变化,即在轮胎侧偏刚度一定的情况下,侧向力与其相应的侧偏角成线性关系,此时车辆可进一步简化为线性二自由度车辆模型。设线性二自由度车辆运动微分方程为:

Yf、Yr分别为轮胎侧向力沿y轴方向的分力。由于前轮和后轮所受到的侧向力与其相应的侧偏角成线性关系,且考虑到前轮转角δf较小,则:

由于车辆失稳的主要原因是由于轮胎的饱相非线性特性所致,为了增加车辆的稳定裕度,往往希望车辆的质心侧偏角响应趋于零。将上式进行拉普拉斯变换,可分别整理得出β和γ对前轮转角δf的响应。
整个控制系统的设计以线性二自由度车辆模型为基础,由于设计的控制系统是根据不同的控制算法对车辆施加附加的横摆力矩,故线性二自由度车辆模型运动方程修正如下:

M2为附加的横摆控制力矩。
2 车辆失稳原因解析及控制策略
2.1 车辆失稳原因
车辆发生失稳大多是在轮胎的非线性区,即随着侧偏角的增加轮胎产生的侧向力逐渐饱和。当前轴发生饱和时前轴就容易发生侧滑,使车辆偏离驾驶员的预期轨迹;当后轴发生饱和而侧滑时容易产生甩尾等更加危险工况。一般认为横摆角速度和质心侧偏角是描述车辆运动状态的重要参数,它们从不同的侧面表征了车辆的稳定性。
2.2 稳定性控制方法与控制策略
为了能够从整车动力学角度对车辆进行自动化控制,通过控制四个车轮的横向和纵向力的分布和幅度控制任何路况下车辆动力学运动模式,大大提高了车辆主动安全特性。
直接横摆力矩控制的基本思想是通过改变车辆内、外侧车轮上的纵向力来产生附加的恢复横摆力矩使车辆稳定性得以改善,该控制方法能显著地改善非线性车辆在弯道加速、减速时的稳定性,进一步提高车辆的操纵稳定性。
文章综合前人工作的基础上,建立的二自由度整车动力学模型,提出一种基于滑模变结构控制理论的直接横摆力矩控制的车辆稳定性控制算法,如前所述,作为这一控制系统,有两控制变量可供选择:横摆角速度与车辆侧偏角。将轨迹和车辆横摆稳定性问题综合在一起。对于这种复杂的非线性系统,不宜使用在线辨识,只能使用鲁棒性控制。
3 滑模变结构控制的基本原理及控制系统的设计
3.1 滑模变结构控制的基本原理
滑模变结构控制是控制系统的一种控制策略。这种控制策略与常规控制的根本区别在于控制的不连续性,即一种使系统“结构”随时间变化的开关特性。该控制特性可以迫使系统在一定特性下沿规定的状态轨迹作小幅度、高频率的上下运动,即所谓的“滑动模态”或“滑模”运动。这种滑动模态是可以设计的,且与系统的参数及扰动无关。这样,处于滑动运动的系统就具有很好的鲁棒性。
3.2 稳定性控制系统的设计
通过前面的分析,可知车辆的质心侧偏角和横摆角速度是车辆稳定性的两个重要状态变量。运用滑模控制理论,以线性二自由度车辆模型为基础,进行电动汽车稳定性控制器的设计。基于控制策略的不同,可以单独控制这两个变量,也可以将质心侧偏角和横摆角速度联合进行控制,因此分别设计了质心侧偏角滑模变结构控制器、横摆角速度滑模变结构控制器、质心侧偏角和横摆角速度联合滑模变结构控制器。
(1)质心侧偏角(β)控制。根据线性二自由度车辆模型,将质心侧偏角对前轮转角的响应,写到滑模面上,质心侧偏角控制的附加横摆力矩:
由到达条件,
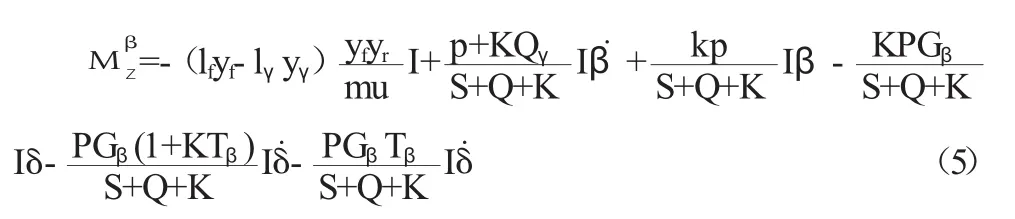
(2)横摆角速度(γ)控制。将横摆角速度对前轮转角的响应,写到滑模面上,横摆角速度控制的附加横摆力矩:
由到达条件,
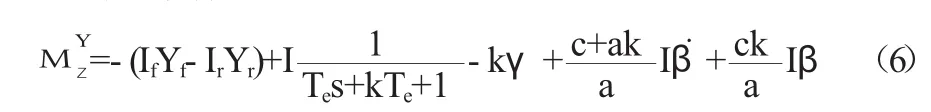
(3)β和γ联合控制。可采用线性表达式确定滑模面的附加横摆力矩:
由到达条件,

4 模型建立与仿真
在Matlab/Simulink环境下有机组合建立电动汽车稳定性控制系统模型并进行仿真分析,验证其在不同路面附着条件下,几种典型的极限工况[5]下控制系统在防止汽车失稳方面的效果,并对几种控制策略进行比较分析。
4.1 汽车稳定性控制系统的仿真模型
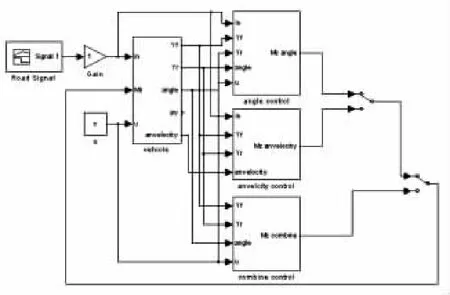
图2 车辆控制系统计算机仿真模型
4.2 汽车稳定性控制系统的效果
仿真中需要给定汽车的前轮转角。通常,汽车在连续转向和突然转向的情况下比较容易出现失稳的情况,采用正弦输入、梯形输入及阶跃输入等输入形式对电动汽车的稳定性进行考察。同时选取道路附着系数分别为0.2、0.4、0.8。如图3、图4、图5所示。
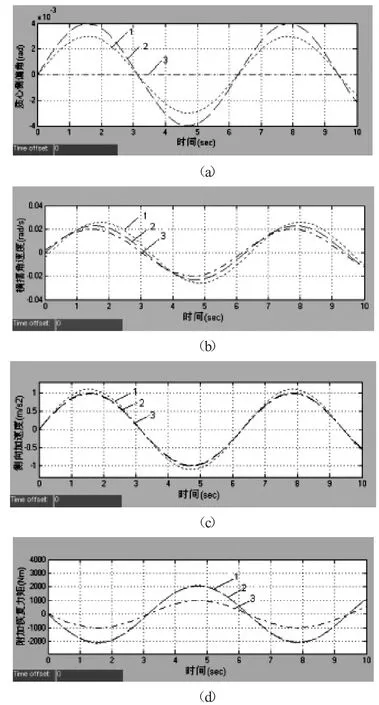
图3 低附着路面控制系统效果仿真(道路附着系数0.2,正弦输入下三种控制策略对比)
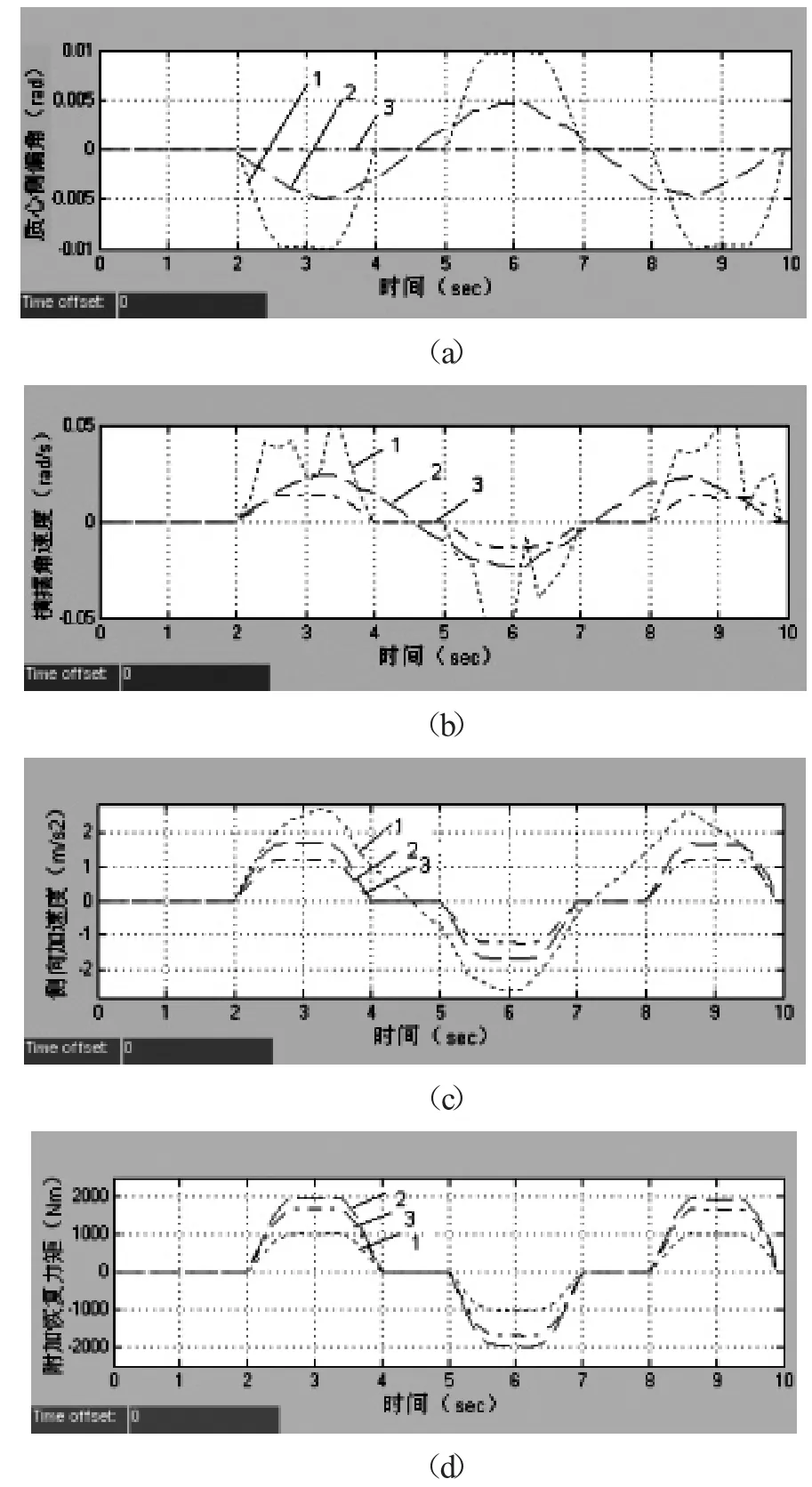
图4 中等附着路面控制系统效果仿真(道路附着系数0.4,梯形输入下三种控制策略对比)
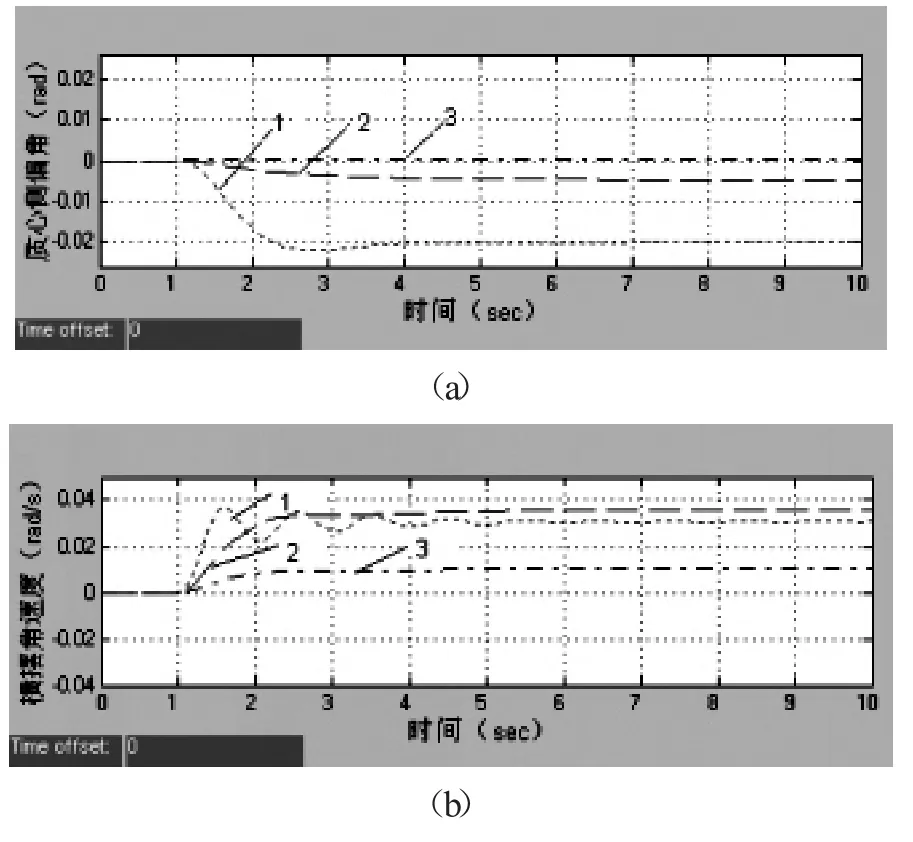

图5 高等附着路面控制系统效果仿真(道路附着系数0.8,阶跃输入下三种控制策略对比)
从图3可看出当车辆在低附着路面上、低速弯道行驶时,主要呈现的是运动学特性,用β控制就能获得较好的效果;而当在高附着路面上、高速弯道行驶时,车辆主要呈现的是动力学特性,从图5可看出此时γ控制的效果显著;而联合控制方法是在某些行驶工况下可以通过联合控制同时抑制汽车质心侧偏角和横摆角速度的变化,达到单独β控制或γ控制无法实现的效果。由此可见,相比单独β控制或γ控制,联合控制方法具有更好的灵活性和适用性。
5 结语
文章在建立线性二自由度车辆模型基础上,基于滑模变结构控制策略的汽车稳定性控制算法的基本理念,进行了控制系统仿真模型的搭建与仿真分析。通过在不同路面附着和不同车速下正弦输入、连续换道和阶跃试验等工况的仿真,对质心侧偏角控制、横摆角速度控制、联合控制这三种控制策略进行了比较分析,可以看出文章所提出的控制方法不仅有效且具有极强的鲁棒性。基于滑模变结构理论的直接横摆力矩汽车稳定性控制算法可在极限行驶工况下显著改善操纵稳定性,防止失稳。并针对不同路面附着控制策略的选择进行了分析讨论,讨论了联合控制参数对控制效果的影响,得出了一些具有指导意义的结论。
[1]余志生.汽车理论[M].北京:机械工业出版社,2001.
[2]郑水波,韩正之,唐厚君.汽车稳定性控制[J].自动化博览,2005,(4):22-24.
[3]赵健.轻型越野汽车牵引力/制动力控制系统研究[D],长春:吉林大学,2007.
[4]Masato Abe,et a1.Side-slip Control to Stabilize Vehicle Lateral Motion by Direct Yaw Moment[J].JSAE Review22,,200l.
[5]闰俊.电动汽车操纵稳定性控制的分析研究[M].北京:北京交通大学.2006.
刘波(1981-),男,硕士研究生,工程师,主要讲师,研究方向:汽车运用。
