基于季节调整和时间序列相混合的中国环县长期风速预测

付 桐 林

(陇东学院 数学与统计学院，甘肃 庆阳 745000)

基于季节调整和时间序列相混合的中国环县长期风速预测

付 桐 林

(陇东学院 数学与统计学院，甘肃 庆阳 745000)

风电系统中，风速是一个关键参数，风速的准确预测可以减少调度错误，增加电网的可靠性。本文给出了基于季节调整法与自回归滑动平均模型(ARMA)和广义自回归异方差模型(GARCH)的相结合的混合预测模型，对2013年环县的月平均风速做出预测。仿真结果表明这种方法要比单独使用ARMA或GARCH预测效果要好，能够准确有效地实现月平均风速的预测。

ARMA；GARCH J-T检验；风速预测；季节调整

Abstract： Wind speed is a key parameter within the wind energy system and the forecasting of wind speed with a high degree of accuracy can minimize the scheduling errors and improve the reliability of power grid.In this paper,the hybrid models based on seasonal adjustment method(SAM)and the ARMA model or the GARCH model are proposed to forecast the monthly average wind speed in 2013 in Huanxian County.The simulation results show that the developed methods have better performance than the ARMA and GARCH model’s,and the monthly average wind speed can be forecasted accurately and effectively.

Keywords： ARMA;GARCH;J-T Test;Wind Speed Prediction;Seasonal Adjustment Method

能源危机促使人类去寻找一种可替代的新型能源，由于风能具有绿色环保和可再生性以及低投入和高收益的优点而备受亲睐。2015年，全球风电产业新增装机63013MW，同比增长22%。其中，中国风电新增装机容量达30500MW，占据了全球新增风电装机容量的28.4%[1]。在风能开发的应用中，风速是关键参数，而准确预测出风速非常困难，这就增加了开发风能的难度。近年来，很多学者根据历史风速数据提出了多种预测方法以期提高风速预测精度[2-4]，但是单独地使用某个模型去预测风速会导致误差较大，因此很多学者又提出了利用混合模型实现风速的预测[5-10]以及利用组合模型去预测风速的方法[4-6]。通常风速预测结果的相对平均误差变化范围是25%到40%[10]，误差来源不仅与预测方法有关，而且与预测时期以及预测区域有关。总的来说，风速预测周期越短，预测地点风速变化越稳定，预测的误差越小。

本文中，我们构建了基于季节调整法(SAM)与自回归滑动平均模型(ARMA)和广义自回归异方差模型(GARCH)相结合的混合预测模型，据此环县月平均风速进行预测，仿真结果表明这种方法要比单独使用ARMA或GARCH预测精度要高。

1 长期风速预测的模型

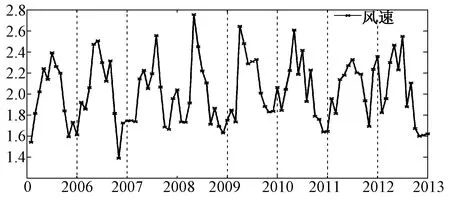
考虑到月平均风速具有季节性差异(如图1所示)，需要对风速时间序列采取消除季节因子的措施，以便实现风速的准确预测。由于ARMA模型和GARCH模型适用于波动性时间序列的预测和分析，近年来有学者使用ARMA模型和GARCH模型来预测风速[2,3]。本文中，我们将这两种方法相结合的预测模型称为SAM-ARMA和SAM-GARCH模型。预测过程包括三个基本阶段:(1)用J-T检验来检验2013年的月平均风速数据集是否具有显著的差异，单位根的检验来检验2006-2013年风速时间序列的平稳性；(2)若没有显著性差异，则采用季节调整法(SAM)消除季节性因素的影响；(3)分别用SAM-ARMA和SAM-GARCH模型来预测风速，并与单独使用ARMA模型或GARCH模型预测风速的精度做比较。

1.1J-T检验

在多个独立样本非参数检验中，J-T检验可以检验多个独立样本的位置参数是否持续上升或下降，确定k组样本是否来自同一总体。J-T的原假设是k组样本来自同一总体或者说它们是来自总体位置参数的总体，其备择假设是各个总体的位置参数按照升序排列或降序排列。J-T检验有两个步骤:

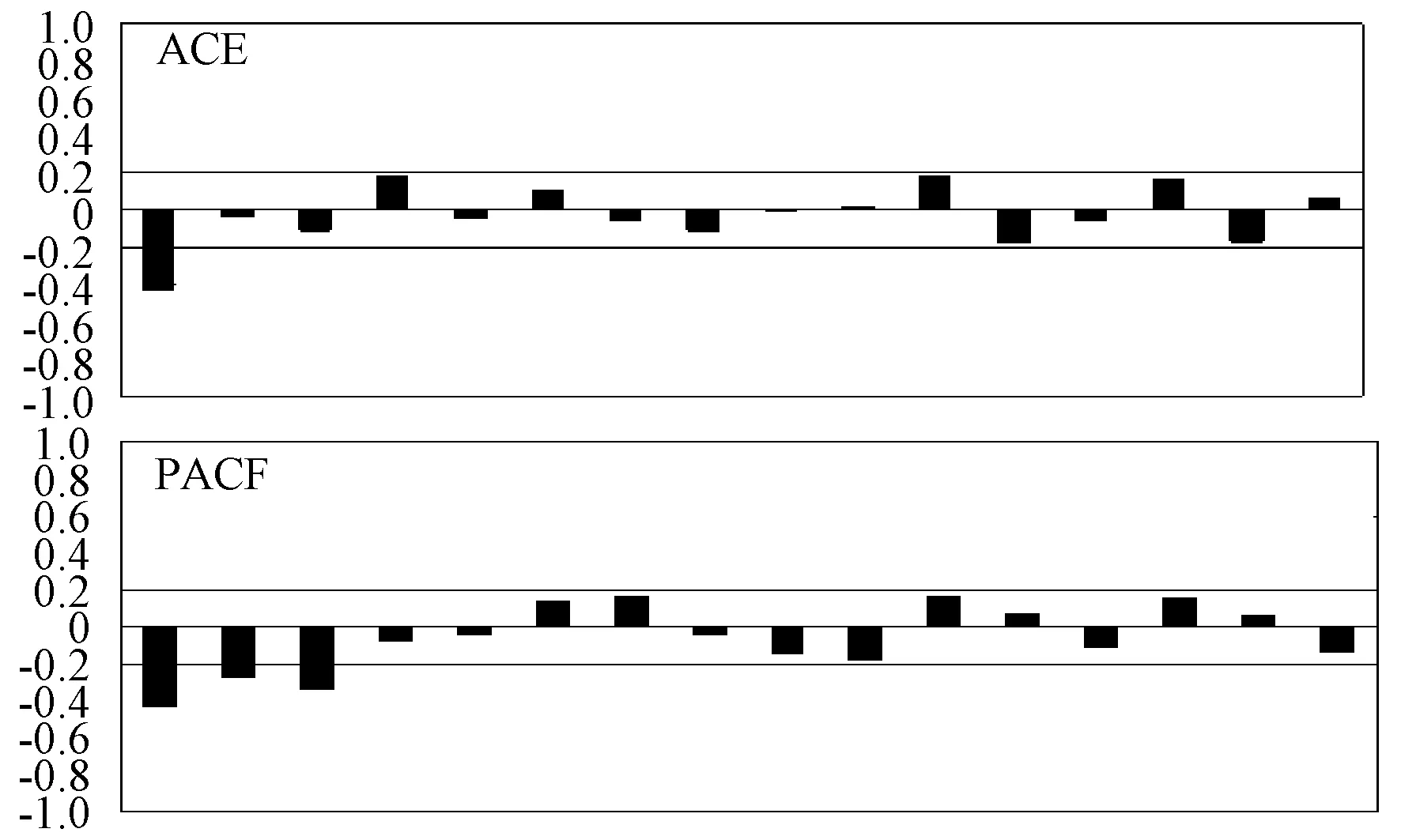
(1)将两组样本值进行对比，计算第i组观测值小于第i′组观测值的对数Mi,i′。设xij是第i组第j个元素，k是样本组数，ni是第i组样本的样本点数。记xi,j

(i=1,…,k;i′=1,…,k;i≠i′)

(1)

(2)计算J-T检验的统计量J=∑Mi,i′。在原假设成立时可以证明统计量：

(2)

具有渐近正态性,即Z～N(0,1)。在给定的显著水平α下求得Z的伴随概率p,如果p值小于显著性水平α,那么拒绝原假设。

1.2季节调整法(SAM)

假设有一系列的数据x1,x2,…,xT(T=ml),可以记为：

x11,x12,…x1l;…;xm1,xm2,…xmlx21,x22,…x2l

(3)

所以：

(4)

季节调整满足归一化条件。通过相应的季节性指数Is对时间序列的每个元素xks进行分割yks=xks/IS,(k=1,2,…,m;s=1,2,…,l),从而得到一个不受季节性因素影响的时间序列。

1.3ADF检验

对时间序列单位根的检验就是对时间序列平稳性的检验,非平稳时间序列如果存在单位根,则一般可以通过差分的方法消除单位根,得到平稳序列。单位根检验是建立ARMA模型的基础。

1.4ARMA预测模型

定义yt为p阶自回归-q阶滑动平均过程,简记为ARMA(p,q):

yt-φ1yt-1-φ2yt-2-…-φpyt-p=

at-θ1at-1-θ2at-2…θqat-q

(5)

或者φ(B)yt=θ(B)at,则称时间序列yt服从(p,q)阶自回归移动平均。p是自回归阶数,q是滑动平均阶数,yi(i=t,t-1,…,t-p)是剔除季节性因素后的时间序列,aj(j=t,t-1,…,t-p)是零均值白噪声参数,φ1,φ2…,φp称为自回归参数,参数θ1,θ2,…,θq称为滑动平均参数。

若p=0,则ARMA(0,q)模型yt=at-θ1at-1-θ2at-2-…θqat-q称为q阶滑动平均模型,记为MA(q)。若q=0,则ARMA(p,0)模型yt-φ1yt-1-φ2yt-2-…-φpyt-p=at称为p阶自回归模型,记为AR(p)。

根据Box-Jenkins提出的方法,用样本自相关函数与偏相关函数的截尾性识别ARMA模型的阶数。若平稳时间序列yt的pk呈q步截尾,而φkk拖尾,则识别序列yt为MA(q)序列;若pk拖尾,而φkk呈p步截尾,则识别序列yt为AR(p)序列;pk和φkk均拖尾,则诊断序列yt为ARMA(p,q)序列[2]。

1.5GARCH模型的构造

1982年美国人Engle开创性地提出自回归异方差模型(ARCH)模型,刻画出随时间而变异的条件方差。1986年,Bollerslev对误差的方差进一步研究,提出广义的ARCH模型,即GARCH模型[2],将GARCH模型运用在时间序列分析上能够更有效地捕捉条件方差的动态特征,特别适合进行波动性预测和分析。记服从(p,q)阶回归GARCH模型的时间序列：

Engle在1982年提出检验残差序列中是否存在ARCH效应的方法有BDS检验、拉格朗日乘数检验(LM)等,其中LM检验是最为常用的检验方法。首先用最小二乘法(OLS)进行参数估计,然后对残差平方项进行辅助回归,再检验所有回归系数是否同时为0,最后在考察异方差原假设成立的前提下,检验统计量nR2是否具有渐近χ2(q)分布[14]。

1.6预测性能的评估

对预测结果进行评价,选择绝对平均误差MAE和相对平均误差MAPE。定义如下:

MAE和MAPE是评价预测精度的重要指标,一般地,MAE和MAPE值越小,预测精度越高。

2 研究区域和数值结果

环县隶属于甘肃省庆阳市,位于甘肃省东部、庆阳市西北部,地处北纬36°1′～37°9′,东经106°21′～107°44′之间,属黄土高原丘陵沟壑区,全境90%以上面积为黄土覆盖,土层厚度在60～240m之间。境内有较大山脉106座,山掌400个,大小沟道17364条,大小残原527块。特殊的地理风貌和长期的农业耕作使得该地区水土流失严重,环境恶化,脱贫致富路途遥远。而这一区域海拔在1136至2089米之间,气候属温带大陆性季风气候,适宜风电场的建设。在国家鼓励新能源建设和精准扶贫的背景下,该区域调整产业结构,优化资源配置,大力发展风电场开发与建设。因此,为了优化风电并网管理和电力负荷预测,以及实现更大规模的风电场建设,亟需对黄土高原陇东区风电场风速做出预测,研究风速对风电项目产生的效益。

原始数据集包含两部分,即2006年～2012年的月平均风速值和2013年的月平均风速值(如图1所示),后者作为评价模型精度的参照对象,用来检验模型的预测效果。对数据集做J-T检验,结果如表1所示,检验的p值为0.591,大于显著性水平0.05,因此接受原假设,即每年的数据集的分布不存在显著差异,即2006～2013的月平均风速数据集包含周期为12的季节波动。

图1 甘肃省环县2006～2013年月平均风速

表1 J-T检验

季节性时间序列可以分解成一个季节性元素Is和非季节性元素yks(yks=xks/Is)的乘积,非季节性元素可以通过很多方法进一步预测。具体方法是基于SAM将原始数据集消除季节因子后,分别用ARMA和GARCH模型进行风速预测,再将季节性因素按照乘法模型加入到预测结果中。

用SAM消除季节因子后的风速序列如图2所示,从图2可以看出：序列波动幅度有所减缓。对于剔除季节性因素的时间序列利用Eviews软件进行单位根检验,判断时间序列是否为平稳序,ADF检验的t统计量的值为-7.2177,分别小于检验水平为1%,5%和10%的t统计量临界值-3.5113,-2.8968和-2.5856,而且t统计量相应的概率p非常小,因此在显著性水平1%,5%和10%下,因此拒绝序列存在单位根的原假设,即剔除季节性因子的时间序列是平稳序列,可以建立ARMA模型计算消除季节因子后的风速序列的自相关—偏自相关函数并绘图如图3所示。

图2 消除季节因子的月平均风速

图3 消除季节因子后风速序列的自相关和偏相关函数图

由图3可知：自相关函数图确定q=1,偏相关函数图确定p=3,选用ARMA(3,1)模型对消除季节因子后的风速序列做出预测。应用SAM-ARAM(3,1)模型预测环县地区2013年的月平均风速并与真实值作图比较,如图4所示。

考虑到风速时间序列的变化特征,我们基于剔除季节性因子的数据又建立了广义自回归异方差模型(GARCH)来预测风速。首先,利用基于最小二乘法的回归模型预测风速,再对回归模型的残差进行ARCH效应检验,检验结果中,概率p的值小于置信水平0.05,因此残差具有ARCH效应,条件方差最优滞后阶数由AIC信息准则选择,并且取SAM-GARCH模型的阶数p=2,q=1。用SAM-GARCH(2,1)模型预测环县地区2013年的月平均风速,并与真实值作图比较,如图4所示：

图4 SAM-ARAM(3,1),SAM-GARCH(2,1)预测值和真实值比较

用MAE和MAPE这两个指标来评价ARIMA(3,1)和SAM-ARIMA(3,1)的预测精度,相关结果见表2：

表2 ARMA(3,1),SAM-ARIMA(3,1),GARCH(2,1),SAM-GARCH(2,1)预测精度

从表2可以看出：SAM-ARMA(3,1)模型和SAM-GARCH(2,1)模型在环县月平均风速预测中有着非常高的预测精度,相对平均误差分别是15.79%和16.29%,比单独使用ARMA(3,1)和GARCH(2,1)预测月平均风速精度要高。这表明在时间序列预测中，将数据预处理的方法(SAM)与传统时间序列分析(ARMA和GARCH)相结合的方法在预测风速中取得了良好的效果。SAM-ARMA(3,1)模型和SAM-GARCH(2,1)模型有优越的预测能力,能够有效提高预测的精准度。

3 结论

风速预测在风电系统中起着重要作用,但是囿于风速的非线性、非平稳性和混沌特性,使得准确预测风速是一个具有挑战性的问题。本文提供了一种基于季节调整消除季节因子的数据预处理方法和时间序列预测模型相混合的风速预测模型来预测环县地区2013年月平均风速,仿真结果显示使用混合方法预测风速精度要比单独使用时间序列模型精度要高,这意味着这种预测方法有着比较满意的预测能力,为风速预测提供了一种可行的预测方法。

[1]http://www.cehome.com/news/20160314/210615.shtml.

[2]ERDEM E,SHI J.ARMA based approaches for forecasting the touple of wind speed and direction [J].Applied Energy,2011,5(88): 1405-1414.

[3]高爽,冬雷,高阳.基于粗糙集理论的中长期风速预测[J].中国电机工程学报,2012,32(1):32-37.

[4]王德明,王莉,张广明.基于遗传BP神经网络的短期风速预测模型[J].浙江大学学报,2015,46(5):837-841.

[5]ZHANG G P,QI M.Neural network forecasting for seasonal and trend time series [J].European Journal of Operational Research,2005(160): 501-514.

[6]GUO Z H,WU J,LU H Y.A case study on a hybrid wind speed forecasting method using BP neural network[J].Knowledge Based Systems,2011(24):1048-1056.

[7]LI G,SHI J.On comparing three artificial neural networks for wind speed forecasting [J].Appl Energy,2010(87):2313-2320.

[8]ZHOU JY,SHI J,LI G.Fine tuning support vector machines for short-term wind speed forecasting [J].Energy Conver Manage,2011(52):1990-1998.

[9]BARTHELMIE R J,MURRAY F,PRYOR S C.The economic benefit of short-term forecasting for wind energy in the UK electricity market [J].Energy Policy,2008(36): 1687-1696.

[10]YANG X,XIAO Y,CHEN S.Wind speed and generated power forecasting in wind farm [J].Proceedings of the CSEE,2005(25): 1-5.

【责任编辑朱世广】

Long-TermWindSpeedPredictioninHuanxianCounty,China—AHybridApproachBasedonSeasonalAdjustmentandTimeSeries

FU Tong-lin

(CollegeofMathematicsandStatistics,LongdongUniversity,Qingyang745000,Gansu)

O212.3；TP391.9

A

1674-1730(2017)05-0005-04

2016-09-30

付桐林(1977—)，男，甘肃民乐人，副教授，硕士，主要从事应用概率统计、能源经济分析及预测理论与方法的研究。