浅析数学中求最值的几种策略

☉浙江省嵊州中学高中部 张铁丽

浅析数学中求最值的几种策略

☉浙江省嵊州中学高中部 张铁丽

在高三的复习迎考阶段，学生经常会碰到一类最值与条件最值问题.这类问题是各地高考、模拟考的热点问题，其特点在于题干往往简洁明了，要求学生从中找到某字母或者表达式的取值范围.在实际的教学中，学生并不能灵活地处理这种题型.只因隔着庐山云雾，学生总认不清最值与条件最值的真面目.基于此，本文将选取常见的几种策略进行阐述.

策略一、化单变量求最值问题

如果二元函数中两个变量之间存在某种等量关系，可以利用代入消元的方式把二元函数化成其中一个字母的函数.

本题中含有字母a，b，故可利用消元思想先将字母b消去，然后将目标函数表示为字母a的函数，利用换元法求出该函数的最值即可.

策略二、构造不等式模型求解最值问题

基本不等式是高中数学的重要模型，最值问题如果能运用基本不等式这一数学模型求解往往可以减小运算量，快速求解.

分析：令2a+b=x，b+1=y（x，y＞0），则a+2b=，出现不等式模型.

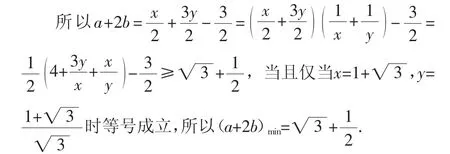
分析：本题如果从解三角形的角度入手，很容易求出OA+OB=sinα ）·，若化简，再用导数求解，运算要求高，不易求出结果.若能用整体的观点研究表达式，设sinα=x，cosα+sinα=y，则OA+OB=（4x+y）），再利用基本不等式求解即可.

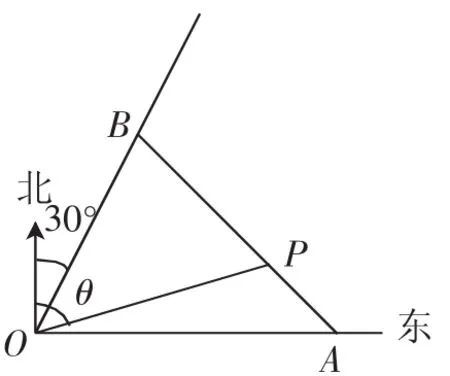
图1

分析：由结构特征很容易想到不等式，难点在于“配凑”，考虑到ab，bc分别和“a2，b2”“b2，c2”产生关系，因此需要将b2拆分，可以利用待定系数法探究系数，令a2+xb2≥ab，（1-x）b2+c2≥2bc

最值问题运用不等式模型求解，往往需要具备整体的意识，配凑出不等式模型“≥2”“x+≥2”“ab≤ ”等.需要注意的是不等式求最值一定要验证等号是否成立.

策略三、构造解几摸型求最值

某些求最值的的问题，若利用数形结合思想，把代数问题转化为几何问题，使问题变得直观具体，且思路清晰，解法往往显得简捷，巧妙.

1.构造两点间距离

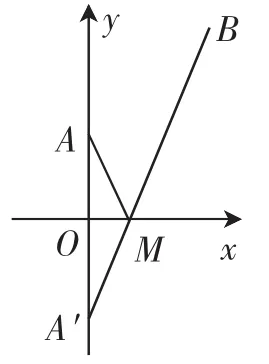
图2

2.构造点到直线的距离

解析：P（x，y）是直线2x+y-8=0上的动点，则d表示点P与点A（0，1）之间的距离，如图3，由点到直线的距离公式知dmin=

图3

3.构造椭圆

例7已知a，b满足4a2=8-b2，试求+的最小值.

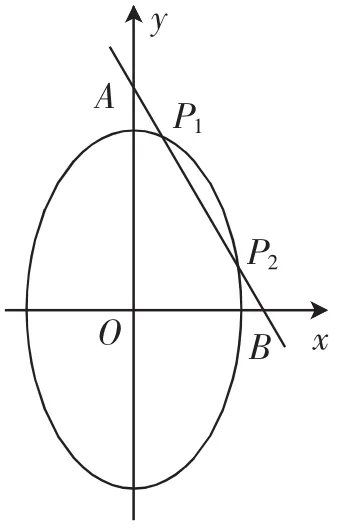
图4

解析：由已知4a2=8-b2得=1，即中心在原点，焦点在y轴上且长轴为4的椭圆，又表示椭圆上点P（a，b）到两定点A（0，3），B（2，1）的距离之和，直线AB：a+b-3=0与椭圆=1有两个交点P1、P2，要使点P到A，B距离之和最小，当且仅当P取P1或P2，如图4，从而的最小值是|AB|=

在平时的教学中，如果我们能对最值问题进行深度剖析，分析其普遍性与特殊性，让学生面对它们时不再“雾里看花、水中望月”，并让他们体验针对具体题型用哪种方法较为合适，养成勤于探究的好习惯.与此同时，学生可以从中发现、欣赏数学的简洁美，找到学习数学的乐趣.