与“线性规划”相关的几个数学问题

☉天津市耀华中学 明廷军

与“线性规划”相关的几个数学问题

☉天津市耀华中学 明廷军

高中数学中的“线性规划”主要是让学生经历从实际情境中抽象出简单的线性规划问题的过程，提高学生数学建模的能力.一般情况下，这一模块的题目整体难度不大，学生对于这一知识点的学习也不够重视.但是实际中与“线性规划”相关的方法与技巧在数学学习中具有很重要的作用，值得我们去学习与研究.本文从如下三个方面进行了介绍.

一、把线性规划问题转化为斜率问题

图1

二、把线性规划问题转化为不等式的恒成立问题

例2已知函数（fx）=a（x-1）2+lnx+1，当x∈［1，+∞）时，若y=（fx）图像上的点都在，所表示的平面区域内，求实数a的取值范围.

所以g（x）max≤0.

（1）当a＞0时，易证：

（3）当a＜0时，g′（x）=在［1，+∞）上g（′x）≤0，所以g（x）在［1，+∞）上单调递减，g（x）≤g（1）=0成立.

综上可知，实数a的取值范围是a≤0.

三、利用线性规划知识巧妙去绝对值

例3若实数x，y满足x2+y2≤1，则|2x+y-2|+|6-x-3y|的最小值是____________.

解析：如图2，由x2+y2≤1，可得6-x-3y＞0，所以|6-x-3y|=6-x-3y.

图2

如图3，直线2x+y-2=0将圆x2+y2≤1分成两部分.

图3

如图4，在直线的上方（含直线），有2x+y-2≥0，即|2x+y-2|=2x+y-2，此时|2x+y-2|+|6-x-3y|=2x+y-2+6-x-3y=x-2y+4.

图4

如图5，在直线的下方（不含直线），即有2x+y-2＜0，即|2x+y-2|=-2x-y+2，此时|2x+y-2|+|6-x-3y|=-2x-y+2+6-x-3y=-3x-4y+8，利用线性规划知识可知，原式不存在最小值.

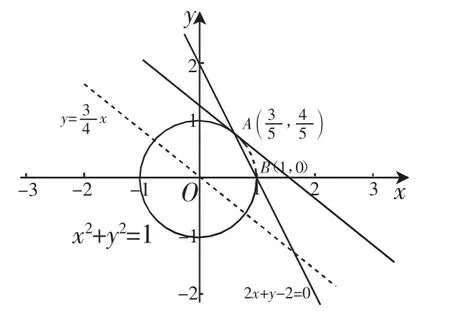
图5

对于线性规划这一方面的题目而言，解题十分烦琐，大多数学生都很抵触，认为解这些题都是一些作图与计算的重复，毫无吸引力可言，结果错失了很多“好题”.这时如何正确地去引导学生显得尤为重要.练习是数学学习的重要环节，但在学生练习的过程当中要引导学生进行习惯性的思考，要有意识地对题目与方法进行归类与提炼，善于发现数学中的美，不能为了练而练，否则会激发学生的厌恶情绪.

张景中老师提出：“一种方法解很多题，要好过很多方法解一个题”.本文就是从“线性规划”的源头出发，不断深入，不断地寻找知识点之间的联系，拓展了学生的视野，极大地丰富了学生对“线性规划”这一知识点的学习.